引 言
双曲守恒律方程通常采用Riemann求解器求解,Godunov、Van Leer和Roe在这方面贡献很大[1-3].通量差分格式在求解双曲守恒律方程中具有理想的特征,用这些格式求解一维问题具有良好的效果,但将其推广到求解二维或高维问题时会产生非物理现象.为了得到鲁棒的数值通量格式,文献[4-7]中给出了一些有效的方法.Levy等[8]给出了计算多维问题的迎风数值方法,这些方法可分为四类:网格一致方法(grid-aligned method)、旋转方法(rotation method)、插值方法(interpolation method)和真正的多维对流格式(genuine multi-dimensional convection scheme);Ren[9]采用旋转Roe Riemann求解器求解Euler方程,该格式能够有效地消除激波不稳定现象;Nishikawa等[10]提出了将HLL通量函数和Roe通量函数相结合的方法,其结果对于激波捕捉具有良好的鲁棒性;Zhang等[11]提出了用旋转迎风格式求解二维问题,其结果能够明显地减少额外的耗散;刘友琼等[12]提出了基于旋转Riemann求解器将HLLC格式和HLL格式进行特定结合得到的一类混合型数值格式,数值算例表明新格式能够消除激波不稳定性.
双曲守恒律方程的初值问题,即使在初始条件充分光滑的情况下,它的解也可能出现间断,因此Lax[13]针对这一情况提出了弱解的概念,在弱解理论下允许存在间断解,但弱解不满足唯一性,因而需要添加一个额外的辅助量来确保其满足唯一性,这个额外的辅助量叫做熵,它在解的光滑区域保持不变,但在激波等间断区域会有所增加.如果构造的数值方法保持总熵不变,也就是熵的局部变化与熵守恒定律完全一致,则称为熵守恒法.熵稳定格式满足守恒律方程的额外条件——熵不等式,使用熵稳定格式得到的解是唯一且满足物理意义的,可以有效避免伪振荡.Ismail和Roe[14]提出了一种新的熵相容格式,该格式是在熵守恒通量基础上加入二阶、三阶的微分项得到熵相容,数值结果显示此格式能够减少非物理振荡;Tadmor[15]构造了一类熵稳定格式,其不包含人为的数值黏性,因而该格式的熵耗散仅由黏性和热流决定;郑素佩等[16]提出了基于移动网格旋转通量法求解二维浅水波方程,该格式选用熵稳定数值通量,通过数值算例可知该算法具有良好的间断捕捉能力和分辨率高的特点.
HLL格式是直接近似单元交界面的数值通量,因而此数值通量是非常鲁棒和有效的Godunov方法.熵稳定格式满足热力学第二定律,可以有效避免伪振荡.因而本文在此基础上提出利用旋转不变性将通量分解为两个正交的方向,每个方向上采用熵稳定格式和HLL格式耦合得到混合的旋转通量格式,最终通过数值算例验证该方法的间断捕捉能力和分辨率.
1 控 制 方 程
考虑二维Euler方程:
(1)
其中
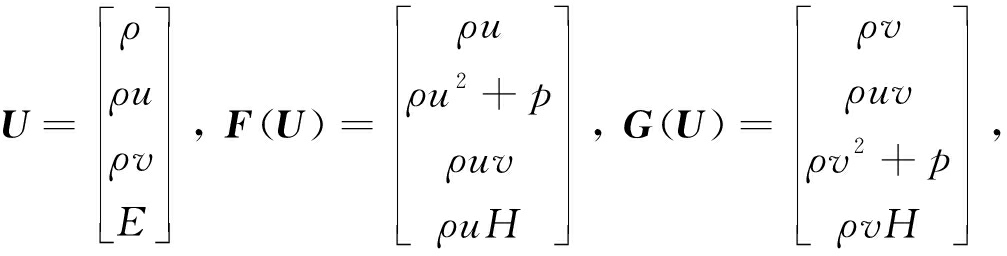
这里ρ是密度,u,v分别是x方向、y方向的速度分量,p是压强,E表示单位体积上的总能量,H表示总焓,
其中γ=1.4是比热比.
2 方程的离散
采用有限体积法[16],将计算区域离散成四边形网格,即控制体为任意四边形单元,其中任意一个单元都有N个界面(二维情况下N=4).对Euler方程两边进行积分可得
(2)
其中V是控制体,A是V的边界,H=(F,G)是通量的张量,n为界面A的单位外法向量.则边界的总通量为
(3)
其中ns是边界s的单位外法向量,ns的分量由角θs确定,θs由单位外法向量ns与x正方向的夹角确定.则式(3)可表示为
(4)
方程(2)的第一个积分项可写为
(5)
将式(4)和式(5)代入式(2)可得
(6)
根据Euler方程的旋转不变![]() 则式(6)可变为
则式(6)可变为
(7)
令![]() 则式(7)右端积分的每一项可写为
则式(7)右端积分的每一项可写为
Ls为AsAs+1的长度.则方程(1)的半离散格式为
其中![]()
时间层上的推进采用三阶强稳定的Runge-Kutta方法[18]:
3 数值通量格式
3.1 熵稳定格式
Tadmor[19-20]提出的熵稳定格式从热力学第二定律出发,满足守恒律方程的额外不等式——熵不等式,所获得的解是具有物理意义的黏性消失解(熵解).该格式由熵守恒通量和数值耗散项构成.
熵稳定格式[14]为
式中![]() 为右特征向量矩阵,
为右特征向量矩阵,![]() 为正的耗散矩阵,HEC为熵守恒通量,可采用算数平均或对数平均[14]计算熵守恒通量中的分量,则HEC=F·nx+G·ny,其中
为正的耗散矩阵,HEC为熵守恒通量,可采用算数平均或对数平均[14]计算熵守恒通量中的分量,则HEC=F·nx+G·ny,其中
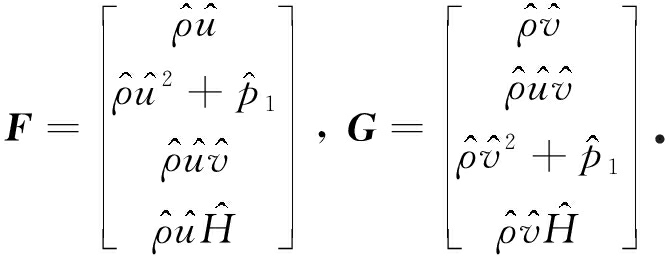
Roe根据Euler方程自身的性质,提出了一种结构简单、计算效率高的熵守恒通量函数[14],该通量函数需选取参变量Z,即
由此可得
其中![]() 是算数平均,即
是算数平均,即![]() 是对数平均,取为
是对数平均,取为![]() 为防止
为防止![]() 的分母为零,可采用文献[18]中的算法计算对数平均.
的分母为零,可采用文献[18]中的算法计算对数平均.
右特征向量矩阵为
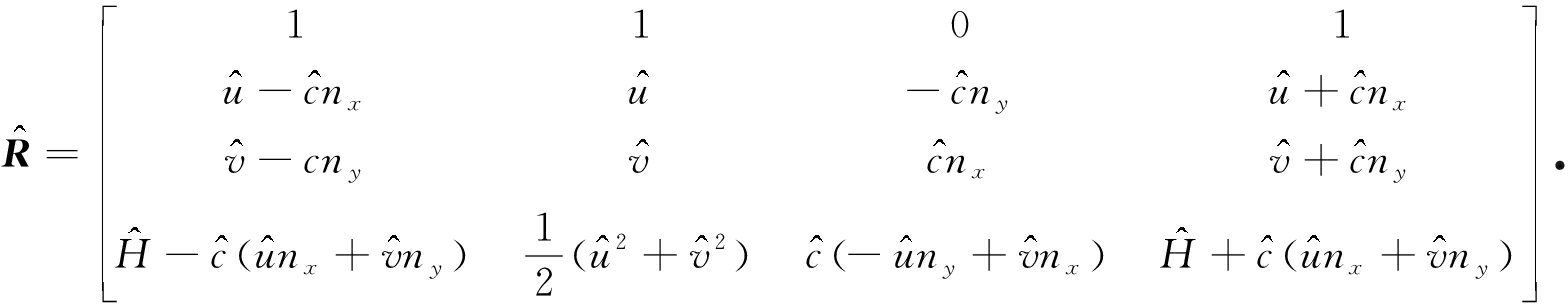
耗散矩阵为![]() 其中
其中![]() 是右特征向量矩阵的特征值的绝对值组成的对角矩阵,
是右特征向量矩阵的特征值的绝对值组成的对角矩阵,
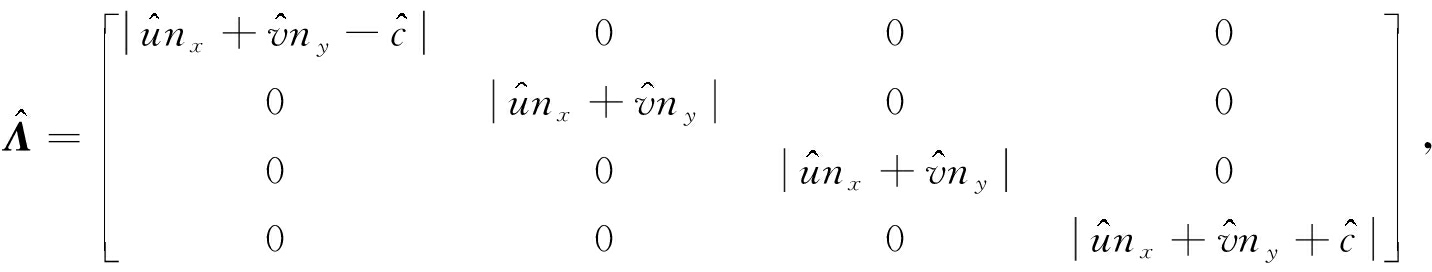
![]() 是比例系数矩阵,
是比例系数矩阵,
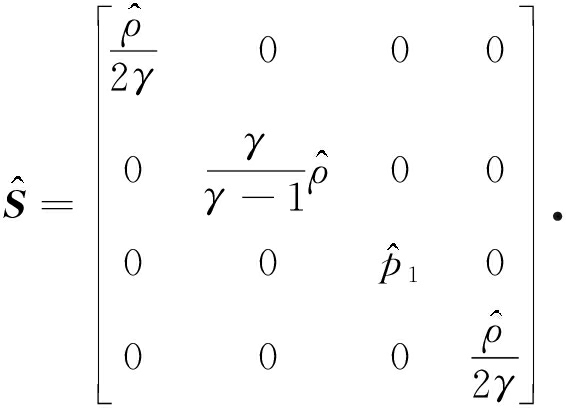
取熵对为
其中s=ln p-γln ρ是Euler方程的物理熵,则对应的熵变量为
3.2 HLL通量
HLL格式最早由Harten等[21]提出,该格式是直接求解单元交界面的数值通量,其主要思想是假设精确解的波形图是由两条波分隔成三个常数区域.HLL格式给出了计算单元通量波速的方法.
HLL通量[12]为
其中![]() 由定义知SR,SL为Jacobi矩阵A=∂H/∂U的最小、最大特征值,
由定义知SR,SL为Jacobi矩阵A=∂H/∂U的最小、最大特征值,
法向量
Roe均值[14]为
3.3 混合格式
根据二维Euler方程的旋转不变性,将法向量n分解成两个正交方向的单位向量n1和n2,每一个方向上采用HLL数值通量和熵稳定通量耦合得到的混合通量格式进行计算.设已知n1,则取与之正交的方向为n2,即n1·n2=0,|n1|=|n2|=1.单元交界面法向量n被投影到这两个正交方向,即
n=α1n1+α2n2, α1=n·n1, α2=n·n2,
则交界面上的混合格式[12]为
Hm=α1HHLL+α2HES.
4 数 值 算 例
算例1 二维Euler方程Riemann问题Ⅰ[22]
在区域[0,1]×[0,1]上求解初值问题:

空间网格数为150×150,取CFL数为0.6,采用周期性边界条件,计算时间t=0.25 s.图1为数值结果等值线图,其中图1(a)的非混合格式结果由单一的熵稳定格式得到,可以看出网格点更多地聚集在弧形激波等间断区域.
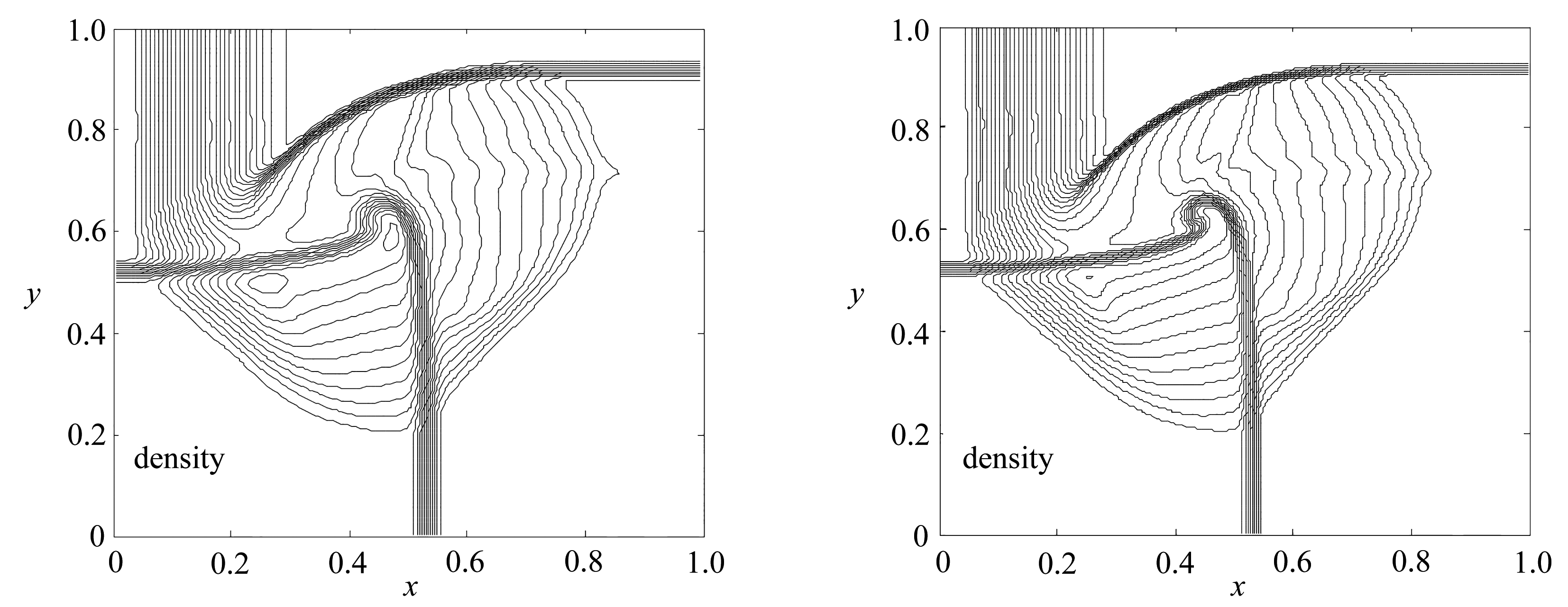


(a) 非混合格式结果 (b) 混合格式结果
(a) Non-mixed scheme results (b) Mixed scheme results
图1 等值线图(算例1)
Fig. 1 Contours(case 1)
比较图1中的(a)和(b)可以看出,旋转通量混合格式的数值结果没有出现振荡或过度抹平现象,因为旋转通量混合格式在网格发生变形的区域利用旋转不变性将通量分解为两个正交方向进行计算,从而激波的过渡带更窄,因而此方法的分辨率更高.
算例2 二维Euler方程Riemann问题Ⅱ[22]
考虑二维区域[0,1]×[0,1]上的Riemann问题,初始条件满足
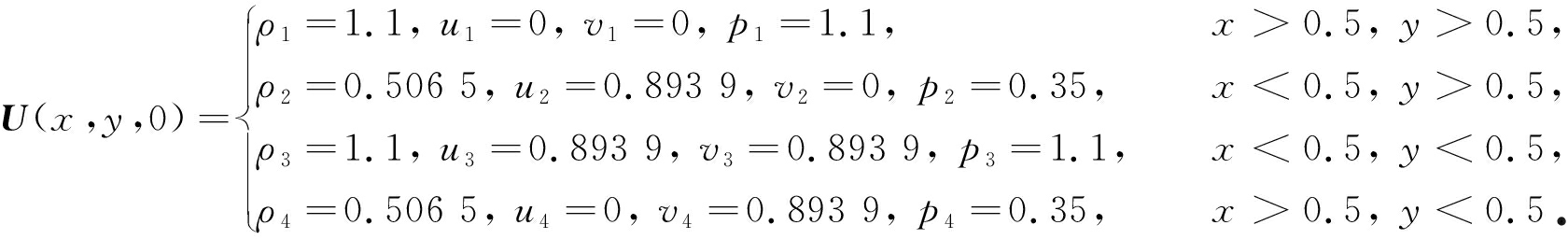

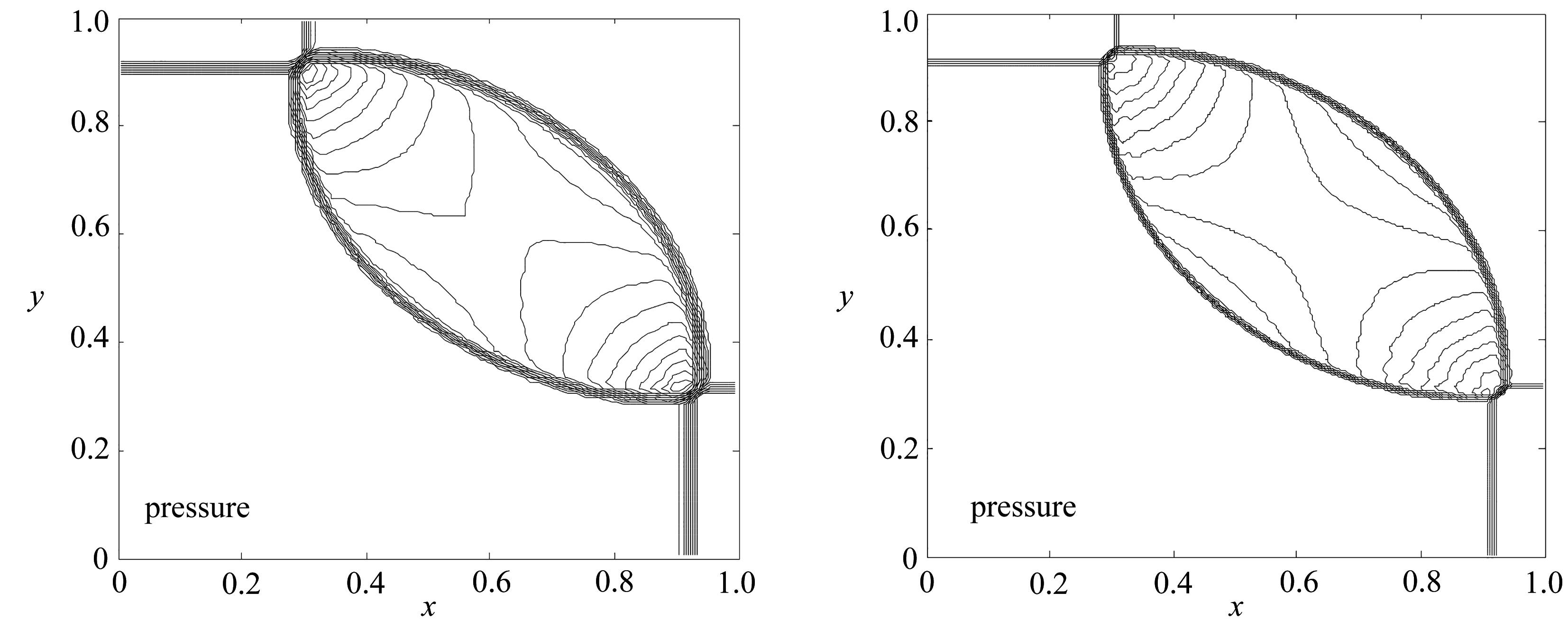
(a) 非混合格式结果 (b) 混合格式结果
(a) Non-mixed scheme results (b) Mixed scheme results
图2 等值线图(算例2)
Fig. 2 Contours(case 2)
空间网格数为150×150,取CFL数为0.6,采用周期性边界条件,计算时间t=0.25 s.图2为数值结果等值线图,其中图2(a)的非混合格式结果由单一的熵稳定格式得到.由图2可以看出,网格主要分布在激波附近,尤其是激波的两个交点附近.比较图2中的(a)和(b)可以看出,虽然两种方法都能捕捉到激波,但采用旋转通量混合格式所得到的结果和非混合格式的结果相比,旋转通量混合格式的过渡带明显变窄,因而该格式的分辨率更高.
算例3 二维Euler方程Riemann问题Ⅳ[22]
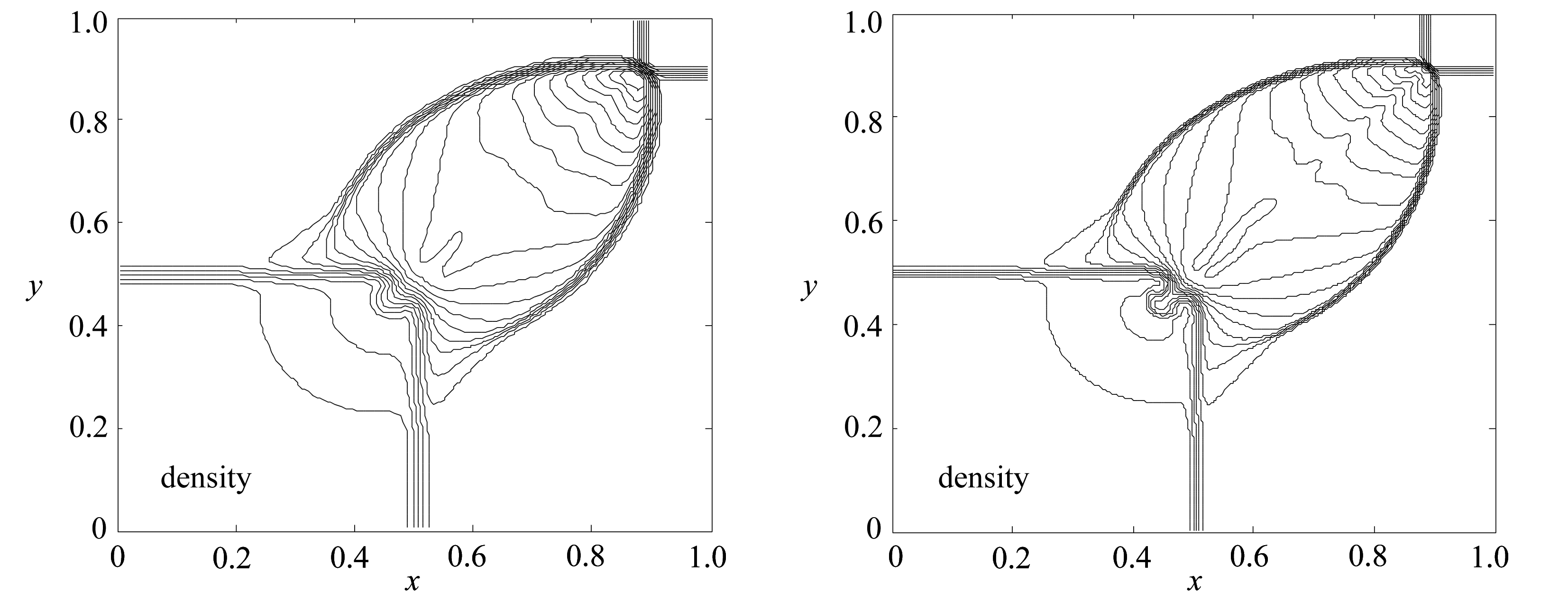
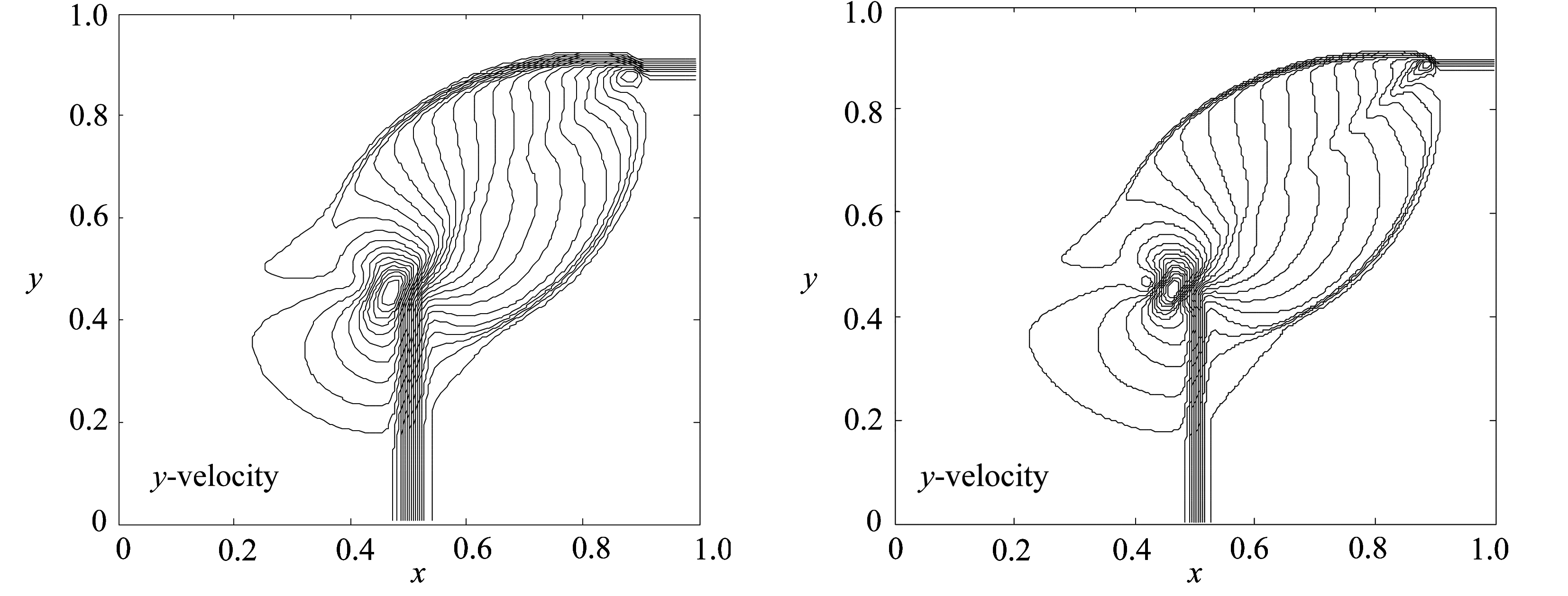
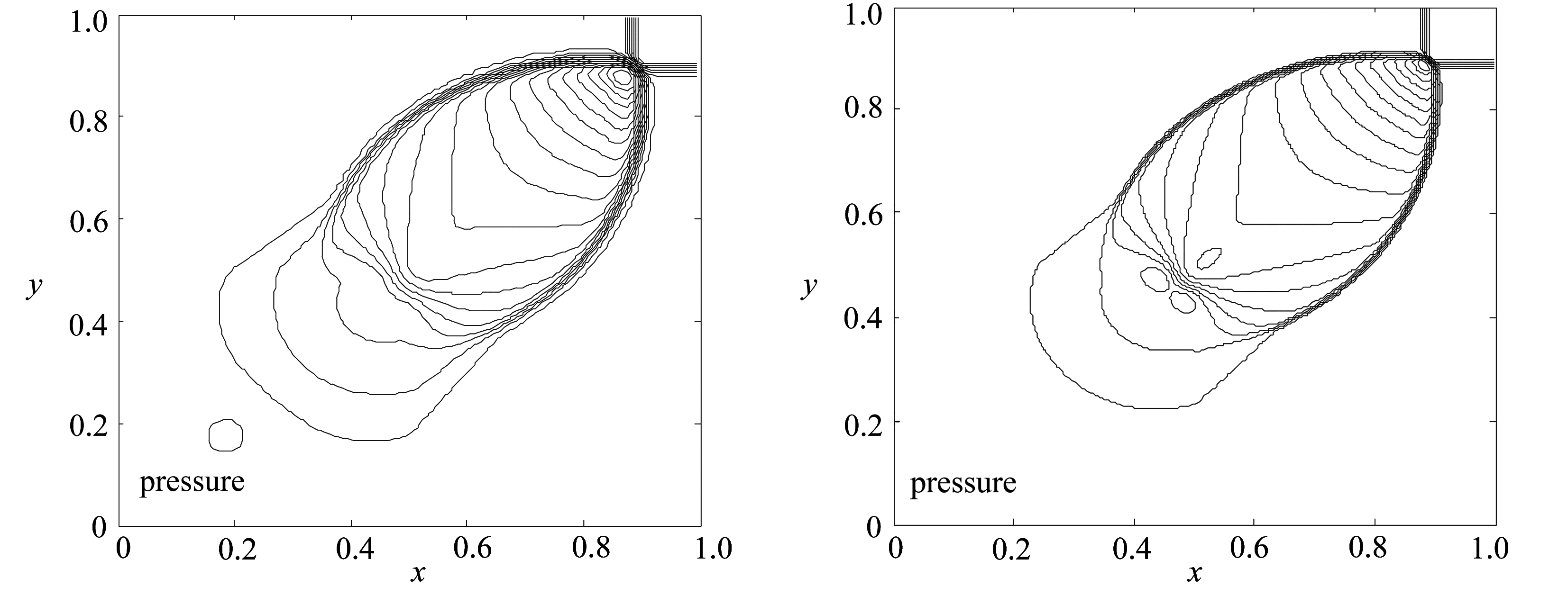
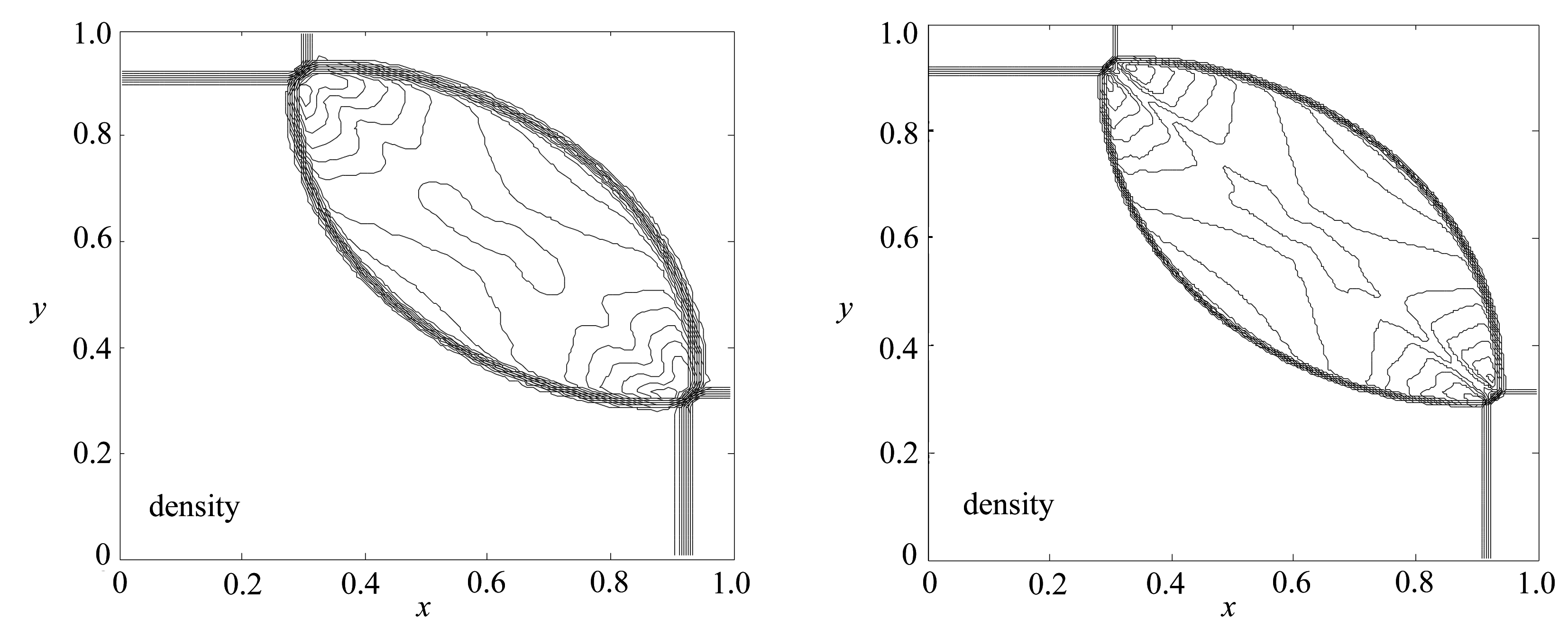
(a) 非混合格式结果 (b) 混合格式结果
(a) Non-mixed scheme results (b) Mixed scheme results
图3 等值线图(算例3)
Fig. 3 Contours(case 3)
考虑二维区域[0,1]×[0,1]上的Riemann问题,其初始条件满足
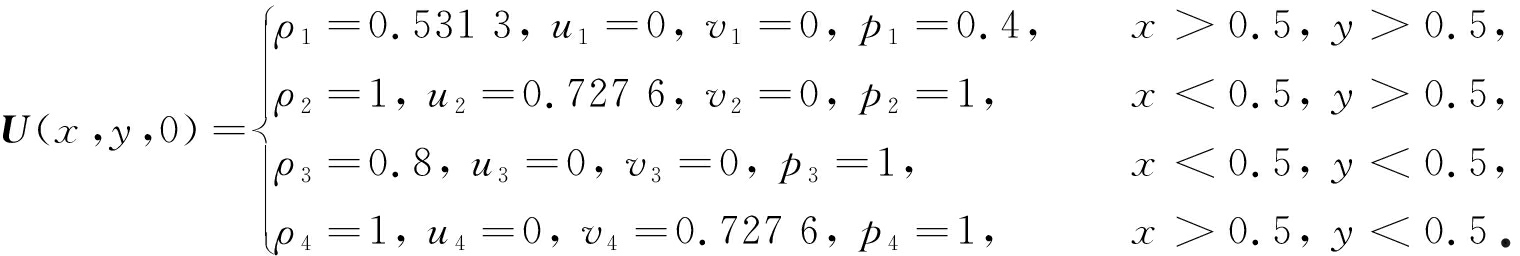
空间网格数为150×150,取CFL数为0.4,采用周期性边界条件,计算时间t=0.2 s.图3为数值结果等值线图,其中图3(a)的非混合格式结果由单一的熵稳定格式得到.由图3可以看出,有更多的网格点分布在间断附近.比较图3中的(a)和(b)可知,两种格式的结果均能有效地展示解的结构,但旋转通量混合格式的结果有了很大的改进,其过渡带更窄且无振荡,因而具有更高的分辨率.
算例4 双Mach反射问题[23]
考虑二维区域[0,4]×[0,1]上的双Mach反射问题,在其底部有一个始于x=1/6的墙,在计算开始时刻,一个Mach数为10的右激波通过点(1/6,0),并与x轴成60°夹角,初始条件为
其中左状态UL、右状态UR和激波的位置h分别为
UL=[8,57.259 7, -33.001 2, 563.544]T,
计算网格为160×40,取CFL数为0.6,计算时间t=0.2 s,上边界需根据激波运动进行分类讨论,下边界于x=1/6处采用无穿透绝热条件,左边界设为流入边界,右边界为流出边界.
图4为数值结果等值线图,其中图4(a)的非混合格式结果由单一的熵稳定格式得到.对比图4中的(a)和(b)可以看出,旋转通量格式的结果有了明显改进,其过渡带更窄,因而分辨率更高.

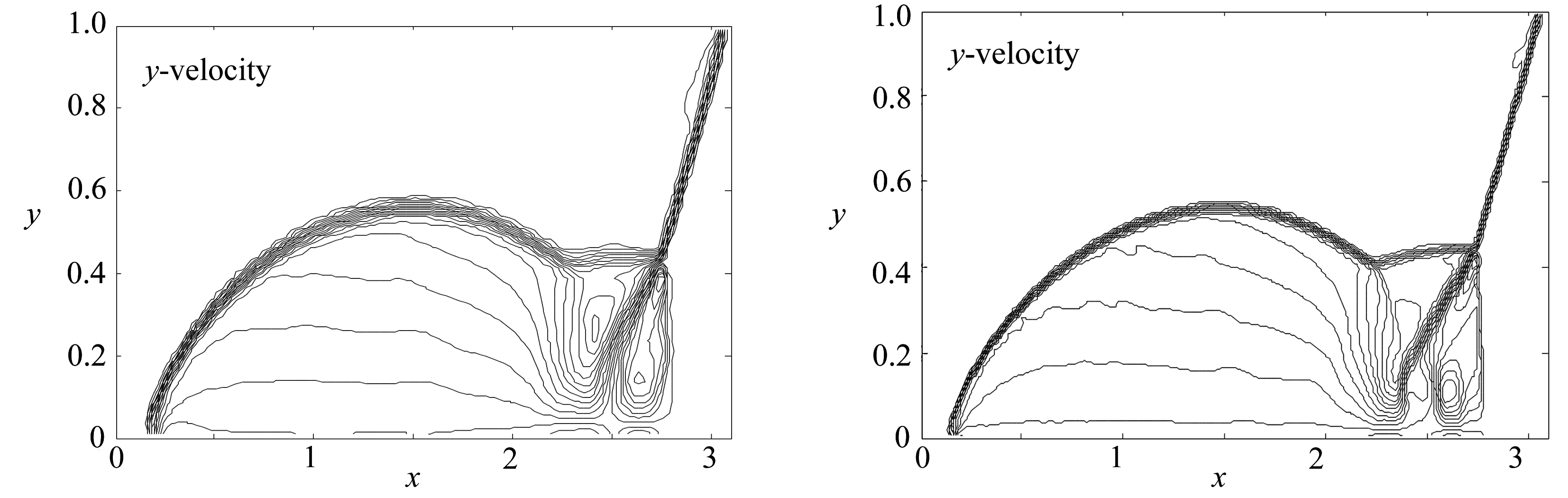

(a) 非混合格式结果 (b) 混合格式结果
(a) Non-mixed scheme results (b) Mixed scheme results
图4 等值线图(算例4)
Fig. 4 Contours(case 4)
5 总 结
本文构造了一个用于求解二维Euler方程的新旋转通量混合格式.利用旋转不变性将熵稳定格式和HLL格式耦合得到混合格式,通过数值算例分析表明,采用本文所提出的方法求解二维Euler方程,激波的过渡带明显变窄,该格式具有良好的间断捕捉能力,分辨率高.本文的通量函数只是一种特殊的组合,还可以采用其他的通量函数进行耦合.
[1] GODUNOV S. Finite difference method for numerical computation of discontinuous solutions of the equations of fluid dynamics[J]. ![]() Sbornik, 1959, 47(2): 271-306.
Sbornik, 1959, 47(2): 271-306.
[2] VAN LEER B. Towards the ultimate conservative difference scheme, Ⅴ: a second-order sequel to Godunov’s method[J]. Journal of Computational Physics, 1979, 32(1): 101-136.
[3] ROE P. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(1): 357-372.
[4] LION M S. Mass flux schemes and connection to shock instability[J]. Journal of Computational Physics, 2000, 160(2): 623-648.
[5] PANDOLFI M, AMBROSIO D. Numerical instabilities in upwind methods: analysis and cures for the “carbuncle” phenomenon[J]. Journal of Computational Physics, 2001, 166(2): 271-301.
[6] QUIRK J J. A contribution to the great Riemann solver debate[J]. International Journal for Numerical Methods in Fluids, 1994, 18(6): 550-569.
[7] SANDERS R, MORANO E, DRUGUET M. Multidimensional dissipation for upwind schemes: stability and applications to gas dynamics[J]. Journal of Computational Physics, 1998, 145(2): 511-537.
[8] LEVY D W, POWELL K G, VAN LEER B. Use of a rotated Riemann solver for the two-dimensional Euler equations[J]. Journal of Computational Physics, 1993, 106(2): 201-214.
[9] REN Y X. A robust shock-capturing scheme based on rotated Riemann solvers[J]. Computer & Fluids, 2003, 32(6): 1379-1403.
[10] NISHIKAWA H, KITAMURA K. Very simple, carbuncle-free, boundary-layer-resolving, rotated-hybrid Riemann solvers[J]. Journal of Computational Physics, 2008, 227(4): 2560-2581.
[11] ZHANG F, LIU J. Evaluation of rotated upwind schemes for contact discontinuity and strong shock[J]. Computer & Fluids, 2016, 134: 11-22.
[12] 刘友琼, 封建湖, 任烔, 等. 求解多维Euler方程的二阶旋转混合型格式[J]. 应用数学和力学, 2014, 35(5): 542-553.(LIU Youqiong, FENG Jianhu, REN Tong, et al. Second order rotational hybrid scheme for solving multi-dimensional Euler equation[J]. Applied Mathematics and Mechanics, 2014, 35(5): 542-553.(in Chinese))
[13] LAX P D. Weak solutions of nonlinear hyperbolic equations and their numerical computation[J]. Communications on Pure and Applied Mathematics, 1954, 7(1): 159-193.
[14] ISMAIL F, ROE P L. Affordable, entropy-consistent Euler flux functions Ⅱ: entropy production at shocks[J]. Journal of Computational Physics, 2009, 228(4): 5410-5436.
[15] TADMOR E. Entropy stable approximations of Navier-Stokes equations with no artificial numerical viscosity[J]. Journal of Hyperbolic Differential Equations, 2006, 3(3): 529-559.
[16] 郑素佩, 王令, 王苗苗. 求解二维浅水波方程的移动网格旋转通量法[J]. 应用数学和力学, 2020, 41(1): 42-53.(ZHENG Supei, WANG Ling, WANG Miaomiao. Solution of 2D shallow water wave equation with the moving-grid rotating-invariance method[J]. Applied Mathematics and Mechanics, 2020, 41(1): 42-53.(in Chinese))
[17] TORO F. Riemann Solvers and Numerical Methods for Fluid Dynamics[M]. Berlin: Springer, 2013.
[18] SHU C W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws[J]. National Aeronautics and Space Administration, 1997, 97(1): 206-253.
[19] TADMOR E. The numerical viscosity of entropy stable schemes for systems of conservation laws: Ⅰ[J]. Mathematics of Computation, 1987, 49(179): 91-103.
[20] TADMOR E. Entropy stability theory for difference approximations of nonlinear conservation laws and related time-dependent problems[J]. Acta Numerica, 2003, 12: 451-512.
[21] HARTEN A, LAX P D, VAN LEER B. On upstream differencing and Godunov-type schemes for hyperbolic conservation laws[J]. SIAM Review, 1983, 25(1): 35-61.
[22] LAX P, LIU X D. Solution of two-dimensional Riemann problems of gas dynamics by positive schemes[J]. SIAM Journal on Scientific Computing, 1998, 19(2): 319-340.
[23] WOODWARD P, COLELLA P. The numerical simulation of two-dimensional fluid flow with strong shocks[J]. Journal of Computation Physics, 1984, 54(1): 115-173.