引 言
平均曲率流方程是一类几何发展方程．它不仅是几何分析领域的典型研究对象(见文献[1-5]),而且在金属结晶等材料科学领域(见文献[6-8])、偏微分方程中边界层理论(见文献[9])等方面也有广泛的应用背景.
在数学上关于平均曲率的研究开始于20世纪80年代．1986年,Gage和Hamilton[1]研究了平面闭曲线Γt以如下方程运动的问题:V=κ, 其中V和κ分别表示曲线Γt的法向速度和曲率．他们证明了任何平面简单凸闭曲线将渐近收缩为一个圆点．1987年,Grayson[2]证明了平面上任何简单闭曲线(不必是凸的)在有限时间内变凸,然后再收缩为一个圆点．1992年和2001年,Chou和Zhu[3-4]考虑了比较一般的平面曲率流:
V=A(n)κ+B(n),
(1)
其中n表示平面简单曲线的单位法向量．在Γt上,他们也给出了闭曲线收敛于圆点的结论.
如果曲线不是闭的,特别是当曲线为函数图像时,关于曲率流也有许多研究．例如,在平面带状区域D={(x,y)|-1<x<1,y∈R},如果曲线Γt是某个函数y=u(x,t)的图像,那么
则方程(1)等价于
(2)
为了保证问题的适定性,当曲线与区域的边界相交时,需要附加一些边界条件．一类广泛使用的边界条件是曲线与区域边界成特定角度:ux(-1,t)=g1,ux(1,t)=g2(参见文献[5]).
1993年, Altschuler和Wu[5]考虑了A=1, B=0, g1<0<g2且g1, g2都是常数的情形, 证明了问题的无界解最终收敛到一个行波解(translating solution):u(x,t)=φ(x)+ct．2011年, Cai和Lou[10]考虑了gi=g±(t)(i=1,2),且gi是周期函数的情形,得到了无界解会收敛到一个周期行波解的结论．2019年,Yuan和Lou[11]考虑了g1=0,g2=g(t,u),且g(t,u(1,t))是渐近周期函数的情形．他们构造了一个整体解(详见下文),这个整体解把负无穷远处(时间和空间上)的周期行波和正无穷远处(时间和空间上)的周期行波连接起来.
由以上工作可知,研究者们已经考虑了对于方程(2)的边界角度为常数、周期函数等情况下的问题．本文将考虑方程中的系数和边界条件均为时间渐近周期的情形,即如下拟线性抛物方程的Neumann边值问题:
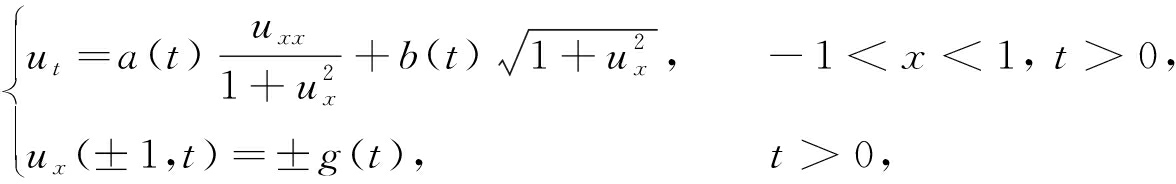
(3)
其中函数a(t),b(t),g(t)满足以下条件:
(H1) a(t),b(t),g(t)∈C1且a(t),b(t)>0.
(H2) 0<g0
inf g(t)<g0sup g(t)<∞.
(H3) 设a(t),b(t),g(t)都是正无穷方向的T+-渐近周期函数,其极限T+-周期函数A+(t),B+(t),G+(t)均为正;也假设它们是负无穷方向的T--渐近周期函数,其极限T--周期函数A-(t),B-(t),G-(t)均为正.
所谓渐近周期函数,其定义如下:
定义1 设p(t)是在R上有定义的函数,称它是正无穷方向上的T+-渐近周期函数:如果存在以T+为周期的函数P+(t), 使得limt→+∞|p(t)-P+(t)|=0．类似地,称它是负无穷方向的T--渐近周期函数:如果存在T--周期函数P-(t),使得limt→-∞|p(t)-P-(t)|=0.
本文将在条件(H1)～(H3)下讨论问题(3)的整体解．所谓整体解就是指时间定义于整个R上的解(见文献[12]及其参考文献)．行波解或周期行波解当然是整体解(关于反应扩散方程格动力系统的这类解参见文献[13-15]等及其参考文献,关于曲率流方程的这类解参见文献[5，10]等)．但是问题(3)中的a(t),b(t),g(t)非常数或周期函数,因此,它不存在行波解或周期行波解,但是我们可以证明它有整体解,而且在正负无穷时间处是渐近于周期行波解的.
1 整体解的存在唯一性
本节研究了整体解的存在性和唯一性.
1.1 整体解的存在性
为了研究问题(3)的整体解的存在性,考虑问题(3)的初值为u(x,0)=ψ(x),x∈[-1,1],其中ψ(x)∈C2([-1,1]),且ψ(x)满足相容性条件:ψ′(1)=g(0),ψ′(-1)=-g(0)．下面考虑一族特殊的问题：
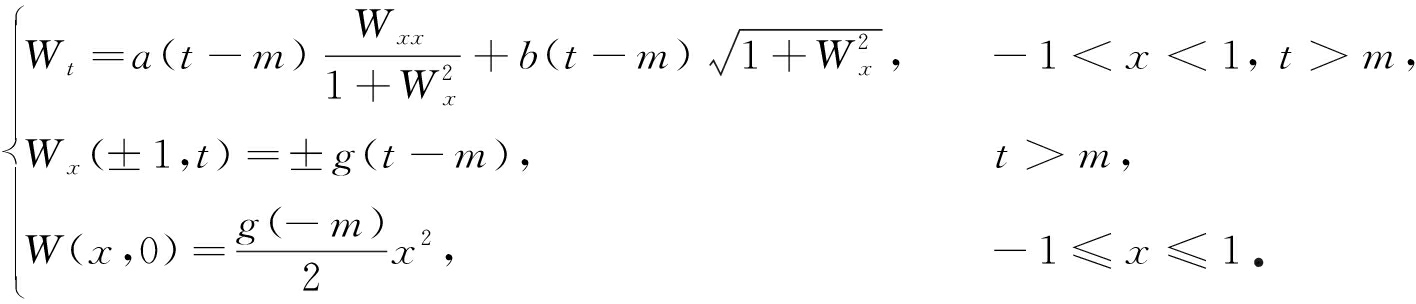
(4)
引理1 若问题(4)中的系数函数a,b,g满足条件(H1)～(H3),则问题(4)的任意全局古典解W(x,t)满足|Wx(x,t)|≤g0,(x,t)∈[-1,1]×[0,+∞).
证明 令η=Wx,对于η满足的问题，利用极值原理的方法可得出结论.
定义2 Um(x,t)=W(x,t+m)-W(0,m),(x,t)∈[-1,1]×[-m,+∞),则Um(0,0)=0.
引理2 由Um(x,t)的定义,得
|Umx(x,t)|≤g0, (x,t)∈[-1,1]×[-m,+∞).
(5)
证明 由Um(x,t)的定义得Umx(x,t)=Wx(x,t),由引理1可直接得出结论.
下面,我们将利用上下解方法对Um(x,t)进行估计．首先考虑如下常系数问题:
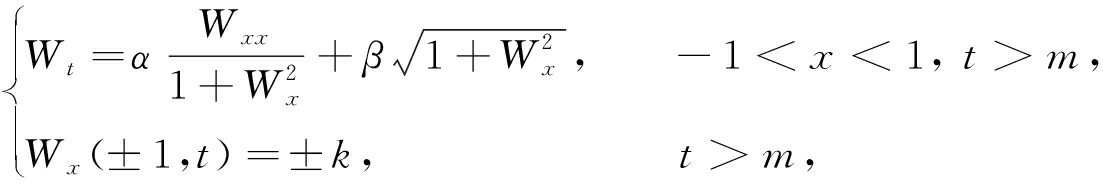
(6)
其中α,β,k都是正数．这个问题的行波解就是形如W(x,t)=φ(x)+ct的解,其中c>β[16]．这里(c,φ)是下面问题的解：
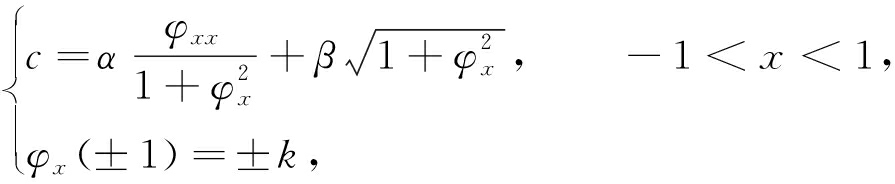
(7)
并且φ(x)满足正规化条件φ(0)=0．当问题(7)有解时,我们记为(c(α,β,k),φ(x;α,β,k)).
命题1[10] 对∀k>0,问题(7)有唯一解(c(α,β,k),φ(x;α,β,k)),且φ(x;α,β,k)满足
|φ(x;α,β,k)|≤k, |φx(x;α,β,k)|≤k, x∈[-1,1].
引理3 对于∀x∈[-1,1],t≥-m,s>-m,存在仅依赖于g0的M>0,使得
c0s-M≤Um(x,t+s)-Um(x,t)≤c0s+M, (x,t)∈[-1,1]×[0,+∞).
(8)
证明 对∀x∈[-1,1],t≥-m,s>-m,令h(x,s)Um(x,t+s)-Um(0,t),则h(x,s)满足
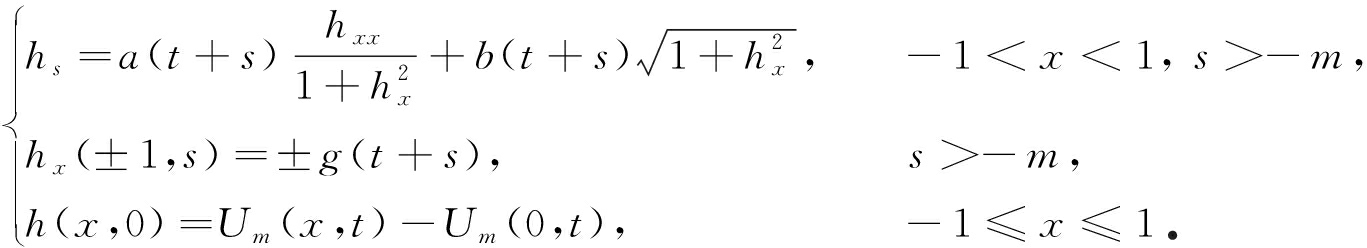
(9)
由式(5)得h(x,0)∈[-g0,g0]．易得到φ(x;a0,b0,g0)+c0s+g0和φ(x;a0,b0,g0)+c0s-g0分别是问题(9)的上下解．根据命题1得
c0s-2g0≤h(x,s)≤c0s+2g0.
(10)
又因为Um(x,t+s)-Um(x,t)=[Um(x,t+s)- Um(0,t)]-[Um(x,t)- Um(0,t)]=h(x,s)-h(x,0),所以c0s-3g0≤Um(x,t+s)-Um(x,t)≤c0s+3g0．令M=3g0,则
c0s-M≤Um(x,t+s)-Um(x,t)≤c0s+M.
引理4 由Um(x,t)的定义得，当t→±∞时,Um(·,t)→±∞.
证明 在式(8)中, 令t=0， 得c0s-M≤Um(x,s)-Um(x,0)≤c0s+M．再令s=t，得c0t-M≤Um(x,t)-Um(x,0)≤c0t+M．因为Um(0,0)=0,|Umx|≤g0,由Lagrange中值定理得|Um(x,0)|≤g0,因此
c0t-4g0≤Um(x,t)≤c0t+4g0.
(11)
由上式得当t→+∞时,Um(·,t)→+∞;当t→-∞时,Um(·,t)→-∞.
引理5 由Um(x,t)的定义得，对∀μ∈(0,1),τ>-m,有
‖Um(x,t)‖C2+μ,1+μ/2([-1,1]×[-τ,τ])≤c0τ+c.
(12)
证明 由式(11)得,当t∈[0,τ]时,-4g0≤Um(x,t)≤c0τ+4g0；当t∈[-τ,0]时,-c0τ-4g0≤Um(x,t)≤4g0．因此|Um(x,t)|≤c0τ+4g0,(x,t)∈[-1,1]×[-τ,τ]．由抛物方程的基本理论[10-11]得估计式(12).
定理1 假设条件(H1)～(H3)成立, 则问题(3)至少存在一个整体解U(x,t),且满足以下性质:
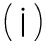U(x,t)∈C2+μ,1+μ/2([-1,1]×R);
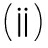|Ux|≤g0;
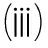对∀t∈R,s>0,x∈[-1,1],存在仅依赖于g0的M>0,使得
c0s-M≤U(x,t+s)-U(0,t)≤c0s+M；
当t→±∞时,U(·,t)→±∞.
证明 由Um(x,t)的定义可得,Um(x,t)满足
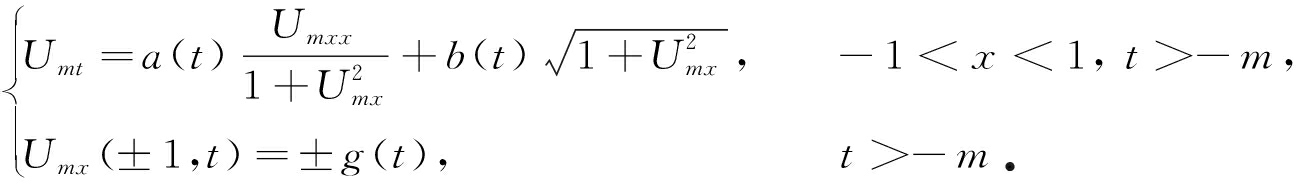
(13)
由式(5)和式(12)得，存在{m}的一个子列{mj}和函数Uτ(x,t)∈C2+μ,1+μ/2([-1,1]×[-τ,τ]),使得limj→∞‖Umj(x,t)-Uτ(x,t)‖C2,1([-1,1]×[-τ,τ])=0．利用Cantor对角化方法,得到{m}的一个子列{m′j}和函数U(x,t)∈C2+μ,1+μ/2([-1,1]×R),使得在
拓扑下,Um′j(x,t)→U(x,t),则U(x,t)是原问题的一个整体解.
令m=m′j,当m→∞时,问题(13)两边取极限,得整体解U(x,t)满足
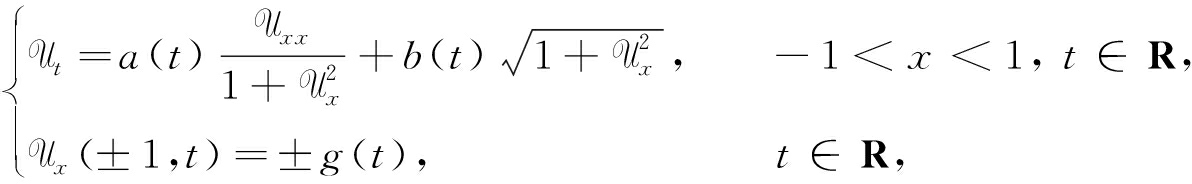
(14)
且 U(0,0)=0.
令m→∞，由式(5)可直接得结论.
由式(10)得c0s-M≤Um(x,t+s)-Um(0,t)≤c0s+M,令m→∞得出结论.
证明过程类似引理4.
1.2 整体解的唯一性
本小节主要研究整体解的唯一性．设U(x,t)和W(x,t)都是问题(3)的整体解,且都满足定理1中的性质～．下面将说明W(x,t)是U(x,t)的一个空间平移．首先对每一个固定的t∈R,定义
D(t)max{D|U(x,t)+D≤W(x,t), x∈[-1,1]},
Λ(t)min{Λ|W(x,t)≤U(x,t)+D(t)+Λ, x∈[-1,1]}.
引理6 函数D(t)和Λ(t)满足以下性质：
D(t)单调递增,Λ(t)单调递减.
当t≥0时,D(t)有界;当t∈R时,Λ(t)有界.
若∃t0,使得Λ(t0)=0,则∃D0∈R,使得对∀t>t0,U(·,t)+D0≡W(·,t);若∃t0, 使得Λ(t0)>0,则对∀t<t0,Λ(t)>0且Λ(t)严格单调递减.
证明 由D(t)和Λ(t)的定义得,对任意固定的t∈R,x∈[-1,1],有
U(x,t)+D(t)≤W(x,t)≤U(x,t)+D(t)+Λ(t).
(15)
令t=t+s,得
U(x,t+s)+D(t+s)≤W(x,t+s)≤U(x,t+s)+D(t+s)+Λ(t+s).
(16)
对式(15),利用极值原理得
U(x,t+s)+D(t)≤W(x,t+s)≤U(x,t+s)+D(t)+Λ(t).
(17)
比较式(16)和式(17),得D(t)≤D(t+s),D(t)+Λ(t)≥D(t+s)+Λ(t+s),所以D(t)单调递增,Λ(t)单调递减.
令χ(x,t)=W(x,t)-U(x,t),则
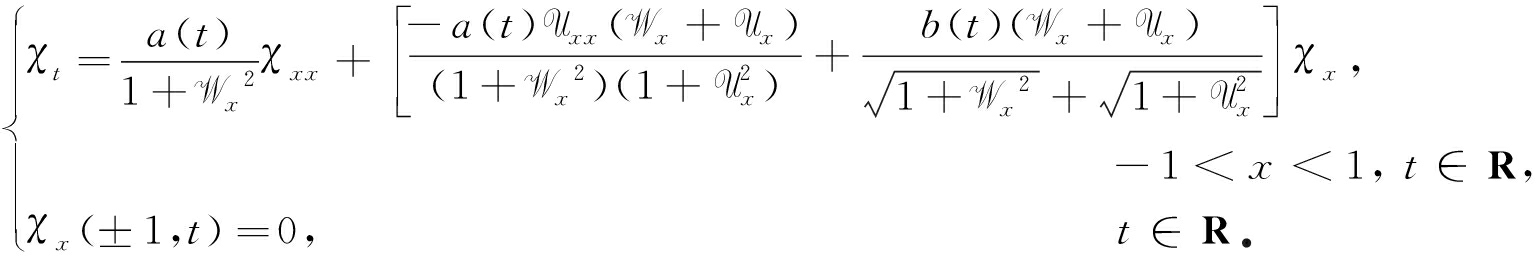
(18)
显然
‖χ(x,0)‖L∞是这个问题的上解,故
从而
由D(t)的定义可知当t≥0时,
下面再证Λ(t)有界．由D(t)和Λ(t)的定义可知,对任何t∈R,存在x1(t),x2(t)使得U(x1,t)+D(t)=W(x1,t),W(x2,t)=U(x2,t)+D(t)+Λ(t)．因此,由|Wx|,|Ux|≤g0及中值定理可得Λ(t)=W(x2,t)-U(x2,t)-D(t)≤4g0+W(x1,t)-U(x1,t)-D(t)=4g0.
若∃t0∈R,使得Λ(t0)=0,那么由D(t)和Λ(t)的定义可知
U(x,t0)+D(t0)≤W(x,t0)≤U(x,t0)+D(t0),
(19)
即U(x,t0)+D(t0)≡W(x,t0),由此可得U(x,t+t0)+D(t0)≡W(x,t+t0),x∈[-1,1],t≥t0．再由抛物方程倒向唯一性定理[17]可知U(x,t)+D(t0)≡W(x,t),x∈[-1,1],t∈R．结论得证.
下面再证∃t0∈R使得Λ(t0)>0的情况．对任何s>0,有
U(x,t0-s)+D(t0-s)≤, ≢W(x,t0-s),
W(x,t0-s)≤, ≢U(x,t0-s)+D(t0-s)+Λ(t0-s),
使用强极值原理,对任何t>0有
U(x,t0-s+t)+D(t0-s)
W(x,t0-s+t)
特别地,当t=s时,有U(x,t0)+D(t0-s)
定理2 设U(x,t)和W(x,t)都是问题(3)的整体解,都满足定理1中的性质～,则W(x,t)是U(x,t)的一个空间平移,即存在D0∈R使得
W(x,t)≡U(x,t)+D0, (x,t)∈[-1,1]×R．
证明 根据引理6,只需证明对∀t∈R,Λ(t)=0即可．设∃t0,使得Λ(t0)>0,由引理6得当t→-∞时,
定义
Un(x,t)U(x,t-n)-U(0,-n), (x,t)∈[-1,1]×R,
Wn(x,t)W(x,t-n)-U(0,-n), (x,t)∈[-1,1]×R,
则Un(0,0)=0,Wn(0,0)=W(0,-n)-U(0,-n)=χ(0,-n),且Un(x,t)满足
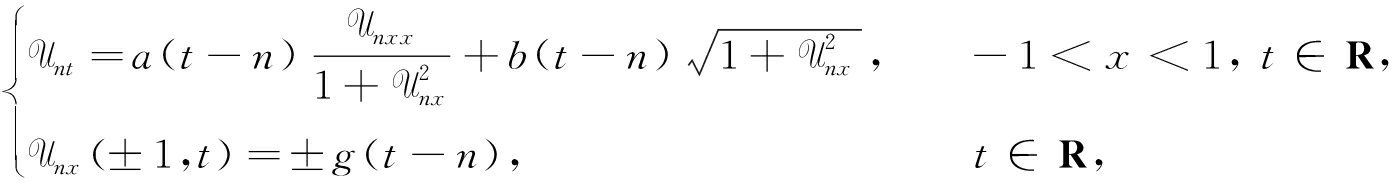
(20)
Wn(x,t)满足
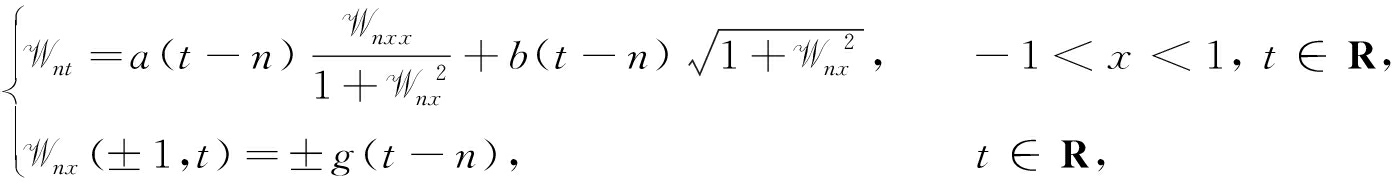
(21)
Un(x,t)和Wn(x,t)都满足定理1中的性质～．类似定理1的证明思路,可得到{n}的一个子列{nj}和问题(20)、(21)的整体解U∞,W∞,使得当j→∞时,在拓扑下,Unj(x,t)→U∞,Wnj(x,t)→W∞．对于整体解Unj(x,t),Wnj(x,t),可以定义对应的Λ(t),不妨记为ΛUnj,Wnj(t)．对于整体解U∞(x,t),W∞(x,t),也可以定义对应的Λ(t),不妨记为ΛU∞,W∞(t)．因此ΛUnj,Wnj(t)→ΛU∞,W∞(j→∞),另一方面
所以
这与引理6矛盾.
2 整体解的ω-和α-极限
本节主要研究整体解的性质,特别是ω-和α-极限．首先定义:
Uk(x,t)=U(x,t+kT+)-U(0,kT+), k∈N+, (x,t)∈[-1,1]×R,
(22)
则Uk(0,0)=0.
引理7 设Uk(x,t)满足式(22)的定义,则对∀μ∈(0,1),τ>-m,有
‖Uk(x,t)‖C2+μ,1+μ/2([-1,1]×[-τ,τ])≤c0τ+c.
(23)
证明 证明思路类似于引理5.
我们需要引用一个周期情况下的结论.
引理8[5] 假设条件(H1)、(H2)成立,如果a(t),b(t),g(t)都是光滑的周期函数,则问题(3)至少存在一个整体解
且
是一个周期行波.
定理3 假设条件(H1)～(H3)成立,则问题(3)的整体解U(x,t)把-∞处的周期行波和+∞处的周期行波连接起来,即
(24)
(25)
其中U+(x,t)和U-(x,t)都是极限问题的周期行波,且k∈N+.
证明 由Uk(x,t)的定义知,Uk(x,t)满足
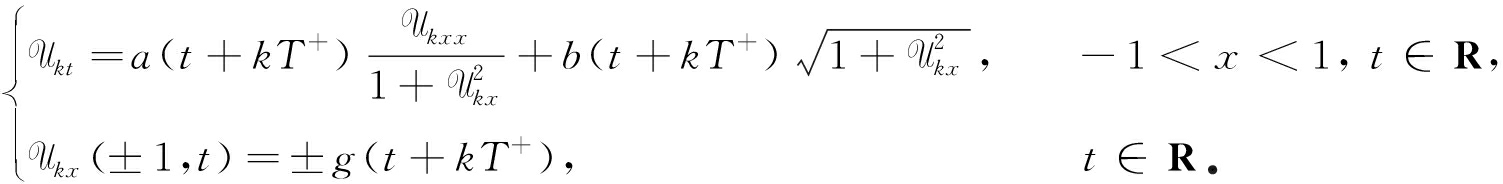
(26)
由|Ukx(x,t)|≤M1和引理7,得到{k}的一个子列{ki}和函数
使得
利用Cantor对角化方法,得到在
拓扑下,Uk′i(x,t)→U+(x,t)．令k=k′i, 当k→+∞时,得limk→+∞U(x,t+kT+)-U(0,kT+)=U+(x,t),即式(24)成立．问题(26)两边取极限得
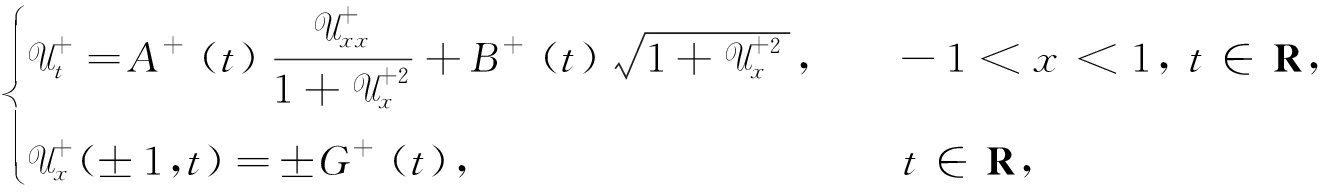
(27)
则U+(x,t)是问题(27)的一个整体解,且U+(0,0)=0．因为A+(t),B+(t),G+(t)是光滑的周期函数,由引理8得U+(x,t)是极限问题(27)的一个周期行波,因此原问题的整体解的ω-极限是一个周期行波.
为了证明式(25),定义U-k=U(x,t-kT-)-U(0,-kT-),k∈N+,利用类似的方法直接得到limk→-∞U(x,t-kT-)-U(0,-kT-)=U-(x,t),且U-(x,t)是相应极限问题的周期行波,因此原问题的整体解的α-极限是一个周期行波.
3 结 论
本文研究了带状区域中具有渐近周期系数和边界条件的曲率流方程,得到了一个时间定义于整个实数轴上的整体解,并刻画了该整体解在正负无穷时间处的ω- 和α-极限,具体地讲:
1) 我们首先考虑了一列特殊的初边值问题,对它们的全局解进行先验估计和重整,从而得到了原问题的一个整体解的结论,并采用向负无穷时间方向重整的办法,得到整体解(除去一个空间平移后)的唯一性.
2) 对于已经得到的整体解,通过向正/负无穷时间处做重整,并进行必要的先验估计,得到了整体解的ω-和α-极限,它们分别是相应的极限问题(不是原问题)的周期行波解．因此,我们的整体解可以理解为像空间中连接两个周期行波解的异宿轨.
本文在理论上有以下创新:所研究的问题具有渐近周期系数,这不同于以往被广泛研究的周期、几乎周期等问题,是有新意和广泛性的课题;对于整体解性质的细致刻画有助于了解原问题完整的动力学行为．此外,本文结论对应用领域中的一些问题也具有参考价值．本文所考虑的模型可以用来描述带状区域的相变过程、晶体生长问题．在表面张力的作用下，界面与区域边界可以形成特定的夹角，在某些情况下,由于区域边界材质的变化,所成夹角也会相应地变化．本文正是对这一类问题进行了研究,可以对相关的应用问题提供理论依据.
致谢 本文作者衷心感谢娄本东教授在论文的撰写过程中提供的细心帮助和指导，以及广东环境保护工程职业学院教研教改项目(J110118061906)对本文的支持.
[1] GAGE M, HAMILTON R S. The heat equation shrinking convex plane curves[J]. Journal of Differential Geometry, 1986, 23: 69-96.
[2] GRAYSON M. The heat equation shrinks embedded plane curves to round points[J]. Journal of Differential Geometry, 1987, 26: 285-314.
[3] CHOU K S, ZHU X P. The Curve Shortening Problem[M]. New York: Chapman & Hall, CRC, 2001.
[4] CHOU K S, ZHU X P. On the existence of two convex hypersurfaces with prescribed kth mean curvature[C]//Partial Differential Equations of Elliptic Type. Cortona, 1992.
[5] ALTSCHULER S J, WU L F. Convergence to translating solutions for a class of quasilinear parabolic boundary problems [J]. Mathematische Annalen, 1993, 295: 761-765.
[6] SMOLUCHOWSKI R. Theory of grain boundary motion[J]. Physical Review, 1951, 83(1): 69-70.
[7] TURNBULL D. Theory of grain boundary migration rates[J]. The Journal of the Minerals, Metals & Materials Society, 1951, 3(8): 661-665.
[8] MULLINS W W. Two-dimensional motion of idealized grain boundaries[J]. Journal of Applied Physics, 1956, 27(8): 900-904.
[9] NAKAMURA K I, MATANO H, HILHORST D, et al. Singular limit of a reaction-diffusion equation with a spatially inhomogeneous reaction term[J]. Journal of Statistical Physics, 1999, 95(5/6): 1165-1185.
[10] CAI J J, LOU B D. Convergence in a quasilinear parabolic equation with Neumann boundary conditions[J]. Nonlinear Analysis: Theory, Methods & Applications, 2011, 74(4): 1426-1435.
[11] YUAN L X, LOU B D. Entire solutions of a curvature flow in an undulating cylinder[J]. Bulletin of the Australian Mathematical Society, 2019, 99: 1-11.
[12] 薛雪. 具有全局交互作用的时滞周期格微分系统的 front-like 整体解[J]. 应用数学和力学, 2020, 41(2): 223-234.(XUE Xue. Front-like entire solutions to lattice periodic dynamic systems with delays and global interaction[J]. Applied Mathematics and Mechanics, 2020, 41(2): 223-234.(in Chinese))
[13] 叶其孝, 李正元, 王明新, 等. 反应扩散方程引论[M]. 北京: 科学出版社, 2011.(YE Qixiao, LI Zhengyuan, WANG Mingxin, et al. Introduction to Reaction-Diffusion Equation[M]. Beijing: Science Press, 2011.(in Chinese))
[14] 曹华荣, 吴事良. 一维格上时滞微分系统的行波解[J]. 应用数学和力学, 2018, 39(5): 592-610.(CAO Huarong, WU Shiliang. Traveling waves of a delayed differential system in a lattice[J]. Applied Mathematics and Mechanics, 2018, 39(5): 592-610.(in Chinese))
[15] 张秋, 陈广生. 一类具有非线性发生率与时滞的非局部扩散 SIR 模型的临界波的存在性[J]. 应用数学和力学, 2019, 40(7): 713-727.(ZHANG Qiu, CHEN Guangsheng. Existence of critical traveling waves for nonlocal dispersal SIR models with delay and nonlinear incidence[J]. Applied Mathematics and Mechanics, 2019, 40(7): 713-727.(in Chinese))
[16] LOU Bendong. Periodic traveling waves of a mean curvature flow in heterogeneous media[J]. Discrete and Continuous Dynamical Systems: A, 2009, 25(1): 231-249.
[17] FRIEDMAN A. Parabolic Differential Equations of Parabolic Type[M]. Englewood Cliffs, NJ: Prentice-Hall, Inc, 1964.