引 言

众所周知，Stokes问题在流体力学中具有广泛的应用．考虑摩擦型非线性滑动边界条件下Stokes方程控制的不可压缩流模型，其二维情形如下:

(1)

其中Ω⊂R2是有界的Lipschitz区域，u(x)是流速的待求向量函数，f(x)是外力的已知向量函数,p(x)是压力的标量函数,ν是黏滞系数且大于零[1-2]．本文考虑如下非线性滑动边界条件:

(2)

其中是标量函数，表示摩擦性能;un=u·n是流速的法向分量，uτ=u·τ是流速的切向分量，n和τ分别表示在边界S上的单位外法向向量和单位切向向量; σn(u)=σ·n是Cauchy压力张量的法向分量，满足σi=σi(u,p)=(νeij(u)-pδij)nj，其中eij(u)=∂ui/∂xj+∂uj/∂xi，i, j=1,2，当i=j时，δij=1,当i≠j时，δij=0.

滑动边界条件是指在边界S上，若切向压力小于给定的临界值g，则流体在边界上不发生滑动; 若切向压力超过临界值g，则流体在边界上发生滑动．针对Stokes问题，前人做了大量的研究工作，主要集中于其解的一些性质，如存在性、唯一性、正则性和连续依赖性等[3-4]．而对于非线性边界条件问题的算法研究相对较少[5-8]，且主要采用Uzawa方法处理非线性[9].

本文对求解具有滑动边界条件Stokes问题的Uzawa块松弛算法进行改进[10-13]，进一步对罚参数的选取给出具体可行的办法: 首先把问题转换为等价的变分问题[5]，再引入一个辅助变量，导出原问题的增广Lagrange函数，得到用其表示的鞍点问题．利用增广Lagrange乘子法，结合Uzawa块松弛算法求解该鞍点问题．由于事先难以通过估计确定合适的罚参数，为了避免其对收敛速度的影响，给出了自动调整罚参数的自适应法则[14]，此算法已成功应用于单侧障碍问题和Signorini问题[15-17]．最后对给出的算法进行收敛性分析，并用数值算例验证算法的有效性.

1 增广Lagrange乘子法

为了方便后面叙述，先定义函数空间:

V={u∈(H1(Ω))2, u|Γ=0, u·n|S=0},

Λ={μ∈L2(S), |μ(x)|≤1, a.e. on S};

和双线性形式:

a(u,v)ν(u,v), b(u,p)=(p，div u)，

其中(·,·)表示向量函数和纯量函数分别在空间(L2(Ω))2和L2(Ω)中的内积．双线性形式a(u,v) 满足正定性: 存在α>0，对∀u∈V有

双线性形式b(u,p) 满足上下确界条件: 存在β>0，对∀p∈M有

其中‖·‖V和‖·‖分别表示在空间V和L2(Ω)中的范数.

根据文献[5]可知，问题(1)和(2)的弱形式等价于以下变分不等式[7,11]:存在(u,p)∈V×M，使得

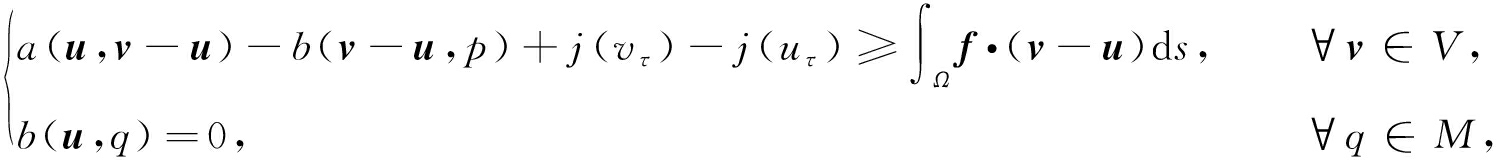
(3)

其中且变分不等式问题(3)等价于以下引理所述的变分等式问题(4).

引理1 假设(u,p)∈V×M是问题(3)的解，则当且仅当存在λ∈Λ使得下式成立:

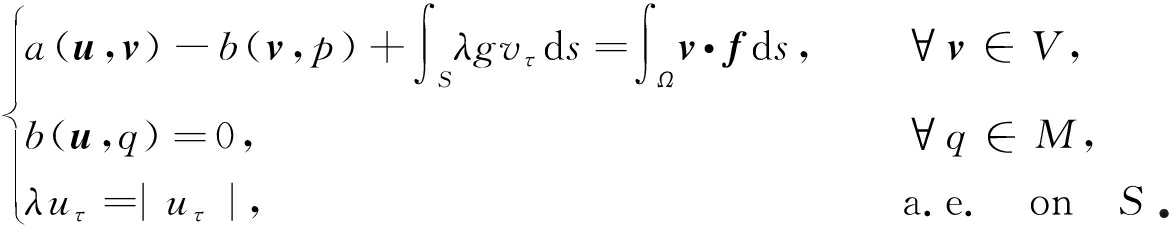
(4)

由文献[6]可知，上述变分问题的第三式等价于

λ=PΛ(λ+ρuτ)， ∀ρ > 0.

(5)

为了求解问题(4)，在边界S上引入辅助变量φ，使得uτ=φ，定义问题(4)的Lagrange函数L:V×M×L2(S)×Λ→R，

(6)

及其增广Lagrange函数:

(7)

其中ρ是罚参数，且ρ>0；v∈V，q∈M，ψ∈L2(S)，μ∈Λ是Lagrange乘子．考虑鞍点问题:寻找(u,p,φ,λ)∈V×M×L2(S)×Λ，使得

Lρ(u,p,φ,μ)≤Lρ(u,p,φ,λ)≤Lρ(v,q,ψ,λ)， ∀(v,q,ψ,μ)∈V×M×L2(S)×Λ.

(8)

由文献[3,5]，可得如下结果.

引理2 若{u,p,λ}是问题(4)的解，则{u,p,φ,λ}是鞍点问题(8)在V×M×L2(S)×Λ上唯一的解，且uτ=φ.

根据引理2，要得到问题(4)的解，只需求解鞍点问题(8)．由文献[10-12]知，可利用Uzawa块松弛算法求解该鞍点问题，算法过程如下.

算法1 Uzawa块松弛算法(UBRM)

第1步 任给初始函数{u(0),λ(0)}∈V×L2(S)，ρ>0，置n=0.

第2步 计算φ(n+1)∈L2(S)，使得

Lρ(u(n),p(n),φ(n+1),λ(n))≤Lρ(u(n),p(n),ψ,λ(n))， ∀ψ∈L2(S).

(9)

第3步 寻找(u(n+1),p(n+1))∈V×M，使得

Lρ(u(n+1),p(n+1),φ(n+1),λ(n))≤Lρ(v,q,φ(n+1),λ(n))， ∀(v,q)∈V×M.

(10)

第4步 更新Lagrange乘子：

λ(n+1)=λ(n)-ρg(u(n+1)-φ(n+1)).

(11)

第5步 给定某种判定条件，如果满足该条件则停止迭代得到数值解(u(n+1),p(n+1)); 否则，置n=n+1，返回第2步.

2 自适应Uzawa块松弛算法及收敛性分析

由于Uzawa块松弛算法的收敛速度显著依赖罚参数，并且事先很难确定合适的参数[10-12]．为了解决这个问题，本文将Uzawa块松弛算法与自适应法则相结合[14-17]，在算法1的基础上得到自适应Uzawa块松弛算法，其计算过程如下[11-12].

算法2 自适应Uzawa块松弛算法(SUBRM)

第1步 任给初始函数{u(0),λ(0)}∈V×L2(S)，ρ>0，置ρn=ρ，n=0.

第2步 计算辅助变量φ(n+1):

(12)

其中 PΛ(μ)=sup(-1,inf(1,μ)), ∀μ∈L2(S).

第3步 求解(u(n+1),p(n+1))∈V×M满足变分问题:

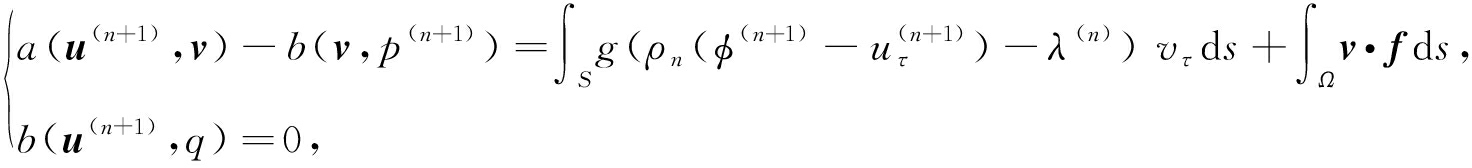
(13)

其中 ∀v∈V，∀q∈M.

第4步 更新Lagrange乘子：

(14)

第5步 选择罚参数ρn+1，使得

(15)

其中序列sn≥0且

关于算法2中第5步罚参数的选取将在数值算例部分详细说明．根据算法2，可得如下收敛性结果.

定理1 算法2产生的序列{u(n),φ(n),p(n),λ(n)} 收敛于{u,φ,p,λ}∈V×L2(S)×M×L2(S)，其中{u,p,λ}是问题(4)的解，且uτ=φ.

证明 令δu(n)=u(n)-u，δp(n)=p(n)-p，δλ(n)=λ(n)-λ,由算法2的第3步，对∀v∈V有

(16)

再由问题(4)有

(17)

将式(16)和(17)相减可得

(18)

因为所以

(19)

在上式中令v=u(n+1)-u，则有

(20)

分别由式(4)的第二式和式(13)的第二式有b(u(n+1)-u,p(n+1)-p)=0，于是可得

即

再根据双线性形式性质可知

(21)

对∀μ∈Λ，如果uτ≠0，因为

根据式(4)的第三式有 和所以

在上式中令得

(22)

由λ∈Λ和投影PΛ的性质可得

(23)

将式(22)、(23)相加得到

(24)

再由式(12)有

将上式代入式(24)得

整理得

(25)

按照算法2中的式(14)有

从而有

由上式及式(25)可得

(26)

由算法2知sn≥0，0<ρn+1<(1+sn)ρn，并由式(21)可得

(27)

将式(26)代入式(27)得

(28)

从而由式(21)有

(29)

令由可得

令

根据式(29)可得

(30)

上式表明：存在一个常数C，使得

(31)

再由式(21)可知{u(n)}和{λ(n)}有界．根据式(28)有

(32)

对上式两边求和可得

(33)

根据双线性性质(21)和式(31)、(33)有

(34)

其中ρL所以

即u(n)在H01(Ω)中收敛于u，进而有φ(n)在L2(Ω)中收敛于φ(φ=uτ).

下证序列{p(n)}收敛于p．在式(19)中取所以有

b(v,p-p(n+1))=a(u-u(n+1),v).

(35)

根据上下确界条件有

(36)

因为u(n)收敛于u，因此有

最后，证明{λ(n)}是收敛的．由于序列{λ(n)}有界，则必有收敛子列．设{λ(ni)}为其收敛子列，令

根据式(12)可得

(37)

因为φ(n)收敛于φ(φ=uτ)，所以对式(37)两边同时取极限可得

λ*=PΛ(λ*+ρnguτ).

(38)

由引理1可知式(38)等价于问题(4)中的第三式，由解的存在唯一性可得λ*=λ，所以{λ(ni)}收敛于λ．假设存在一个使得可得由于λ和u分别是{λ(n)}，{u(n)}的一个收敛点，则存在n0≥0使得

(39)

由式(21)、(30)和(39)可知，对∀ni≥n0，有

(40)

即对∀ni≥n0有

与假设矛盾，所以即{λ(n)}收敛于λ.

3 数 值 算 例

本文利用自适应Uzawa块松弛迭代算法求解具有滑动边界条件的Stokes问题，迭代过程中通过迭代函数自动调整罚参数，用变参数ρn代替固定参数ρ[14-17],从而达到提高算法效率的目的．下面具体考虑算法2中选取罚参数ρn的自适应法则．根据算法的收敛性证明，由式(27)知下式成立：

为了利用平衡加快收敛，我们希望

在上式中分别用替代λ，uτ可得

从而可采用如下法则选择变参数ρn: 给定一个正常数τ>0，若

则在下次迭代时ρn变小;若

则在下次迭代时ρn变大．综上，令

可得如下选取罚参数的自适应法则:

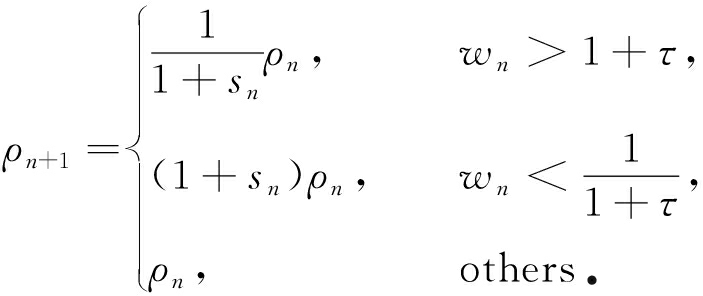
序列{sn}按照如下方式得到:

其中cmax是一个正常数，cn表示ρn改变的次数，即

显然序列{sn}满足在数值算例中，我们取τ=2和cmax=100.

为了验证算法的有效性，我们给出一个数值算例[6]．设Ω是单位正方形区域，边界∂Ω由Γ和S两部分组成，其中Γ={(0,x2)|0<x2<1}∪{(x1,0)|0≤x1≤1}∪{(1,x2)|0<x2<1}，S={(x1,1)|0≤x1≤1}．给出在黏性边界条件u|∂Ω=0下Stokes问题的解:

(41)

设黏性系数ν=1，其中外力f为

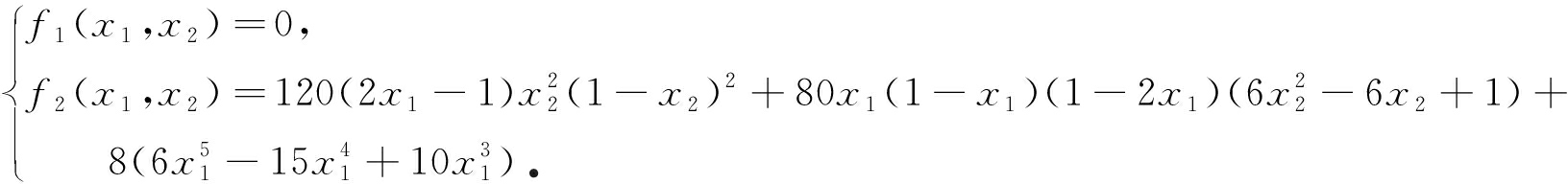
通过直接计算，可得

显然当摩擦因数g>1.25时，不发生滑动现象，根据式(41)可得精确解; g≤1.25时，则发生滑动现象,式(41)得到的解就不再是一个精确解，因此我们就需要更精细的网格的近似解作为参考[6]．取罚参数ρ=1和步长h=1/20，并用算法2求解，g=0.8 和g=2流速u的数值解分别如图1、图2所示.

从图中可以清晰地观察到，当g=0.8时发生滑动现象; 当g=2时不会发生滑动现象．这与理论分析和精确解结果是一致的.

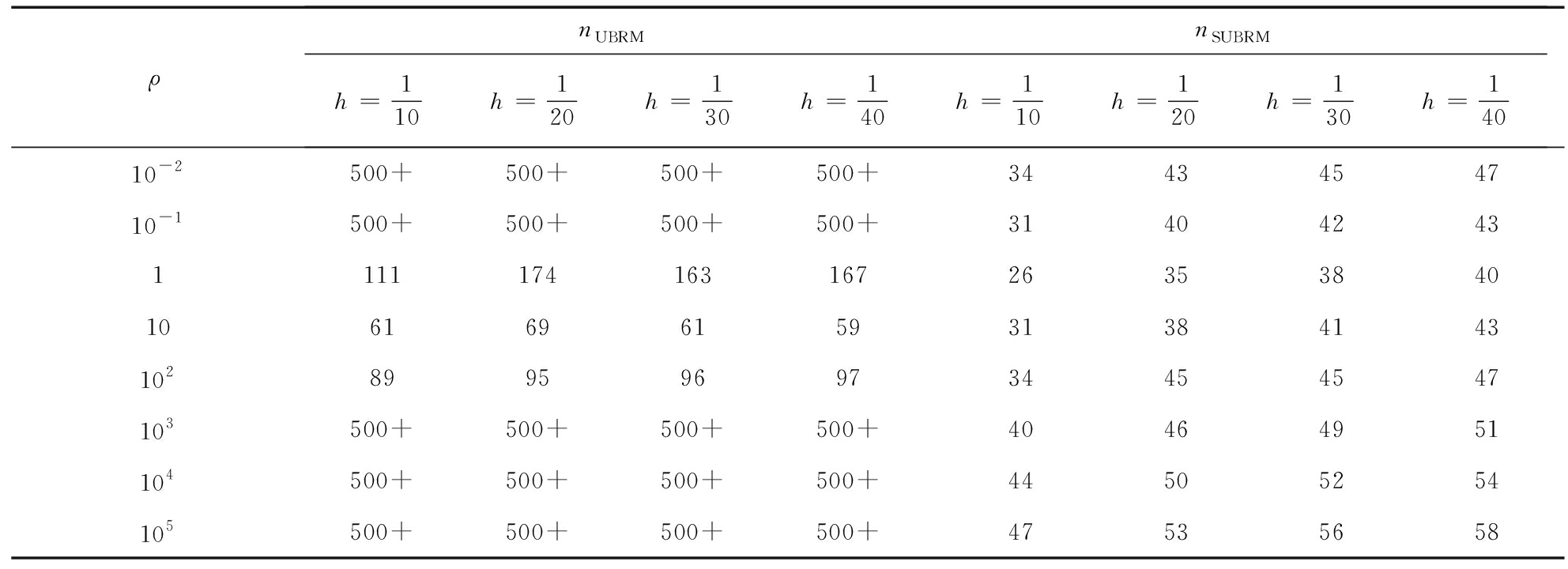
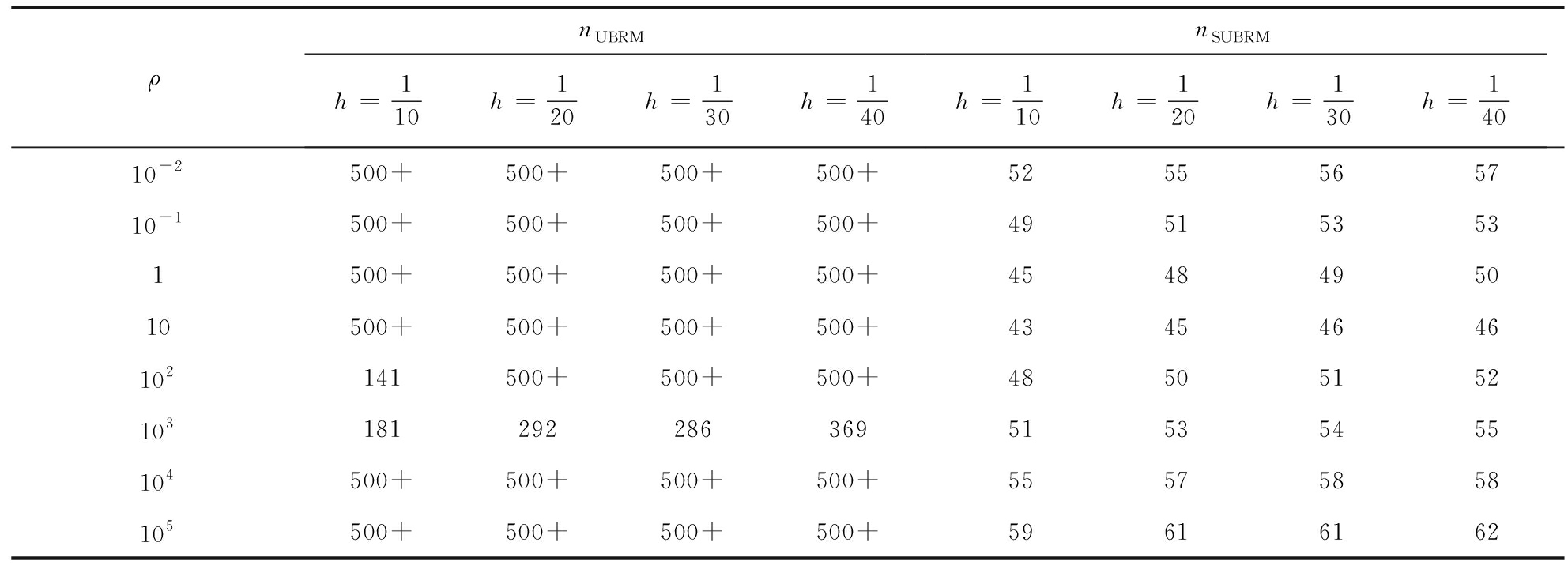
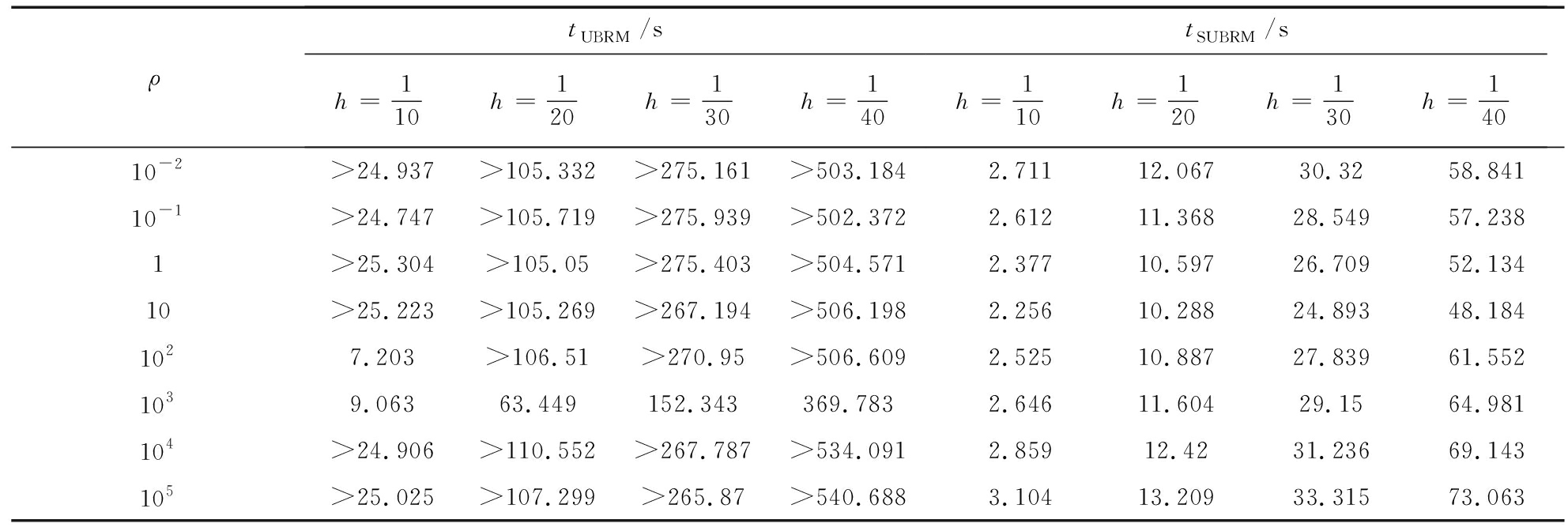
在此考查罚参数的自适应法则效果，取不同的初始罚参数ρ和步长h，分别采用Uzawa块松弛算法和自适应Uzawa块松弛算法对g=0.8和g=2的问题进行数值计算，所对应的迭代次数和CPU运行时间见表1～4，其中“500+”表示迭代次数超过500．表中数值结果表明，自适应Uzawa块松弛算法收敛速度及运行速度明显优于Uzawa块松弛算法，并且对所有的罚参数具有较好的稳定性.

4 结 论

本文提出了求解滑动边界条件下Stokes问题的自适应Uzawa块松弛算法．该算法不仅计算简单，并且给出的自适应法则可以利用迭代函数自动选择合适的罚参数，有效解决了Uzawa块松弛算法的迭代次数高度依赖于罚参数ρ的不足的问题，从而显著提高了算法性能．数值结果表明了该算法的优越性.

参考文献（References）：

[1] 黄鹏展, 何银年, 冯新龙. 解Stokes特征值问题的一种两水平稳定化有限元方法[J]. 应用数学和力学, 2012, 33(5): 588-597.(HUANG Pengzhan， HE Yinnian， FENG Xinlong. A two-level stabilized finite element method for the Stokes eigenvalue problem[J]. Applied Mathematics and Mechanics, 2012, 33(5): 588-597.(in Chinese))

[2] SHI D Y, PEI L F. Superconvergence of nonconforming finite element penalty scheme for Stokes problem using L2 projection method[J]. Applied Mathematics and Mechanics (English Edition), 2013, 34(7): 861-874.

[3] FUJITA H. A mathematical analysis of motions of viscous incompressible fluid under leak or slip boundary conditions[J]. RIMS Kky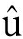roku, 1994, 888(1): 199-216.

[4] SAITO N. On the Stokes equation with the leak and slip boundary conditions of friction type: regularity of solutions[J]. Publications of the Research Institute for Mathematical Sciences, 2004, 40(2): 345-383.

[5] LI Y, LI K T. Uzawa iteration method for Stokes type variational inequality of the second kind[J]. Acta Mathematicae Applicatae Sinica(English Series), 2011, 27(2): 303-316.

[6] KASHIWABARA T. On a finite element approximation of the Stokes problem under leak or slip boundary conditions of friction type[J]. Japan Journal of Industrial and Applied Mathematics, 2013, 30(1): 227-261.

[7] JING F F, LI J, YAN W J. Discontinuous Galerkin methods for a stationary Navier-Stokes problem with a nonlinear slip boundary condition of friction type[J]. Applied Mathematics Letters, 2017, 73(2): 113-119.

[8] 周康瑞, 尚月强. 带非线性滑移边界条件的Stokes方程的一种并行有限元算法[J]. 西南师范大学学报(自然科学版), 2020, 45(5): 32-38.(ZHOU Kangrui, SHANG Yueqiang. A parallel finite element algorithm for Stokes equations with nonlinear slip boundary conditions[J]. Journal of Southwest China Normal University (Natural Science Edition), 2020, 45(5): 32-38.(in Chinese))

[9] 饶玲. 单调迭代结合虚拟区域法求解非线性障碍问题[J]. 应用数学和力学, 2018, 39(4): 485-492.(RAO Ling. Monotone iterations combined with fictitious domain methods for numerical solution of nonlinear obstacle problems[J]. Applied Mathematics and Mechanics, 2018, 39(4): 485-492.(in Chinese))

[10] GLOWINSKI R. Numerical Methods for Nonlinear Variational Problems[M]. Berlin: Springer-Verlag, 2008.

[11] KOKO J. Uzawa block relaxation method for the unilateral contact problem[J]. Journal of Computational and Applied Mathematics, 2011, 235(8): 2343-2356.

[12] DJOKO J K, KOKO J. Numerical methods for the Stokes and Navier-Stokes equations driven by threshold slip boundary conditions[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 305(15): 936-958.

[13] 王光辉, 王烈衡. 基于对偶混合变分形式的Uzawa型算法[J]. 应用数学和力学, 2002, 23(7): 682-688.(WANG Guanghui, WANG Lieheng. Uzawa type algorithm based on dual mixed variational formulation[J]. Applied Mathematics and Mechanics, 2002, 23(7): 682-688.(in Chinese))

[14] HE B S. Self-adaptive operator splitting methods for monotone variational inequalities[J]. Numerische Mathematik, 2013, 94(4): 715-737.

[15] 郭楠馨, 张守贵. 自由边界问题的自适应Uzawa块松弛算法[J]. 应用数学和力学, 2019, 40(6): 682-693.(GUO Nanxin, ZHANG Shougui. A self-adaptive Uzawa block relaxation algorithm for free boundary problems[J]. Applied Mathematics and Mechanics, 2019, 40(6): 682-693. (in Chinese))

[16] ZHANG S G. Projection and self-adaptive projection methods for the Signorini problem the BEM[J]. Applied Mathematics and Computation, 2017, 74(6): 1262-1273.

[17] ZHANG S G, LI X L. A self-adaptive projection method for contact problems with the BEM[J]. Applied Mathematical Modelling, 2018, 55: 145-159.

A Self-Adaptive Uzawa Block Relaxation Method for Stokes Problems With Slip Boundary Conditions

ZHANG Maolin, RAN Jing, ZHANG Shougui

(School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, P.R.China)

Abstract: A self-adaptive Uzawa block relaxation method was designed for Stokes problems under nonlinear slip boundary conditions. For the variational formulation of the problem, an auxiliary unknown was introduced to transform the problem into a saddle-point one based on an augmented Lagrangian function, which can be solved with the Uzawa block relaxation method. To improve the performance of the method, a self-adaptive rule was proposed with the proper penalty parameter chosen automatically. The main advantage of this method is that each iterative step consists of a linear problem while the auxiliary unknown can be computed explicitly. The convergence of the algorithm was analyzed. The numerical results show the feasibility and effectiveness of the proposed method.

Key words: Stokes problem; slip boundary; Uzawa block relaxation method; self-adaptive rule; augmented Lagrangian function

中图分类号： O221.6

文献标志码：A

DOI：10.21656/1000-0887.410170

*收稿日期： 2020-06-11； 修订日期：2020-07-25

基金项目： 国家自然科学基金(11971085);重庆市自然科学基金(cstc2020jcyj-msxmX0066);重庆市高校创新研究群体项目(CXQT19018);重庆市研究生教育优质课程项目(201949)

作者简介：

张茂林(1995—), 女, 硕士生(E-mail: 674003207@qq.com);

张守贵(1973—), 男, 教授, 博士, 硕士生导师(通讯作者. E-mail: shgzhnag@cqnu.edu.cn).

引用格式: 张茂林, 冉静, 张守贵. 具有滑动边界条件Stokes问题的自适应Uzawa块松弛算法[J]. 应用数学和力学, 2021, 42(2): 188-198.