引 言
传统的投资组合模型是结合收益和风险指导投资者的决策行为．Markowitz[1]最早提出了均值-方差的投资组合模型，模型的均值和方差分别表示投资组合的收益和风险，这成为了投资定量化研究的开端，为研究更加符合实际金融市场的投资组合模型提供了理论支持．均值-方差模型有效的前提是无摩擦因素市场，但近年来受国家政策以及投资者多样性等因素的限制，影响金融市场交易费用、背景风险等已不容忽视．Arnott等[2]研究表明忽视交易费用会导致投资组合达不到最优．Morton等[3]研究了固定交易费用对投资组合的影响，证明了即使较小的交易费用也对投资策略有较大的影响．另外，背景风险[4]也算是投资组合模型不容忽视的因素，背景风险是受收入状况、社会关系、生活开销以及健康状况等因素的影响，并且不能通过对资产的分配而分散的风险．Heaton等[5]研究了基于劳动收入的背景风险对投资组合的影响．李佳等[6]研究了是否含有背景风险和背景风险偏好度大小(包括背景风险为零和非零的情况)对投资组合的影响，证明了含有背景风险的投资组合模型优于不含有背景风险的模型．玄海燕等[7]研究了背景风险对个人投资者最优决策的影响，并证明了随着投资者对背景风险的偏好度的增加，其受影响程度会降低．此外，同样能够影响投资者决策的因素是证券的流动性，证券的流动性[6]是指证券的变现能力，是证券市场中衡量证券优劣的一个重要指标，目前使用较广泛的是用换手率度量证券流动性．一般认为，换手率越高，股票交易越频繁，资金进出市场较容易，具有较强的变现能力，即股票的流动性越好；反之，换手率越低，股票的流动性越差.
传统的投资组合模型往往依靠历史数据估计证券收益，但受各种经济因素和社会因素的影响，并不是总能得到精确可靠的历史数据．因此对于实际金融市场的不确定性，模糊集(数)是刻画模糊信息的一种重要的工具，这也为模糊投资组合的研究提供了有力的支撑．Dubois和Prade[8]定义了模糊数的区间期望值，并证明了模糊数具有可加性．Carlsson和Fuller[9]用模糊数表示投资组合的收益率，并对模糊数的上下可能性均值、清晰可能性均值以及清晰可能性方差和协方差的定义和性质加以运用和扩展．Zhang等[10]在上述研究的基础上，从新的视角对清晰可能性均值和方差重新定义和补充，并将其定义和性质与上述学者的成果进行对比分析，给出了它们之间的区别和联系．李婷、张卫国等[11]将非金融风险中的背景风险考虑进投资组合模型中，分析了一般模糊收益和模糊正态收益下的投资组合模型，并将可信度作为一个约束条件．邓雄、徐维军等[12]建立了以投资者满意度为目标，同时考虑背景风险和弹性增量等因素的模糊投资组合模型．李佳等[13]提出了基于最大满意度和背景风险的模糊投资组合模型，此模型将最大化投资组合收益与最小收益证券的差值作为目标函数.
在对模糊投资组合的研究中，绝大数学者均用方差度量投资组合的风险，而方差是通过非线性积分来定义的，若增加对风险资产的投资数量，则会导致方差和各风险资产之间的协方差计算量较大或者难以计算，较大地增加了模型的求解难度．针对上述的求解缺陷，本文利用二阶矩作为风险的度量函数，较方差优越的是其计算并不复杂且关于参数具有凸性，简化了模糊投资组合求解问题．为了符合现实金融市场不确定的发展特性，从模糊性的角度考虑投资组合问题，同时考虑了对投资者有较大影响的背景风险及证券的流动性，在前提为有交易费用的摩擦市场中，建立一个包含背景风险和证券流动性的模糊投资组合模型．然后，用梯形模糊数和固定可能性分布下的梯形模糊变量表示证券的收益率和换手率，用对称三角模糊数表示背景风险的收益率，用投资组合收益率的二阶矩作为风险的度量函数，在对预设期望收益率、期望换手率水平以及各风险资产的投资比例约束下建立目标为风险最小的模糊投资组合模型．最后，通过数值计算与分析，说明考虑背景风险和流动性的投资组合模型对实际金融市场具有适用性，为投资者提供一定程度上的模型参考.
1 预 备 知 识
我们首先回顾一些有用的定义和定理.
定义1[14] 假设论域为U，指定一个从U到[0,1]的映射
则称该映射在论域U上确定了一个模糊子集
简称为模糊集，表示为：
其中
表示u对模糊集
的隶属度函数，
称为u的隶属度．所有的模糊集一般用f(U)来表示.
定义2[15] 假设U为论域，且是U的模糊数，则需要满足4个条件：
1) 隶属度函数必须是上半连续函数；
2) 对于任意的
的γ-截集均为凸的；
是正规集，即∃u0∈U，有
的支集在论域U中存在有界性，即
是有界的.
定义3[10] 设A∈F(x)，∀γ∈[0,1]，记[A]γ={x∈X|A(x)≥γ}，称[A]γ为模糊集A的γ-截集，或称γ-水平集，记为[A]γ=[a1(γ),a2(γ)].
定义4[13] 若一个模糊数可以表示为
且隶属度函数满足下式，则称是一个梯形模糊数．其中，α表示梯形模糊数的左宽度，β表示右宽度，[a,b]称为容许区间．其隶属度函数如下，相应的函数图形如图1所示：
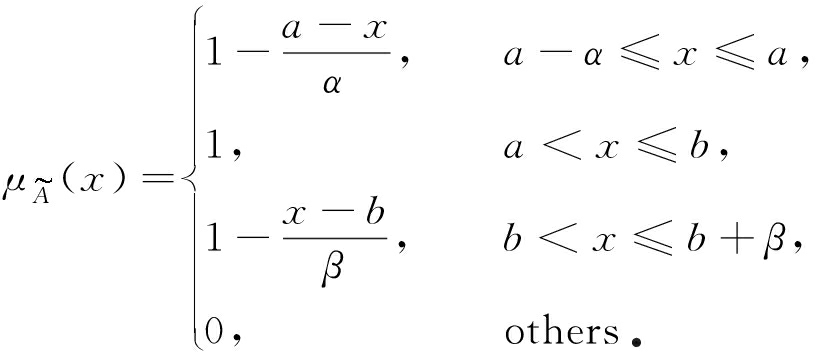
定义5[10] 若一个模糊数可以表示为
且隶属度函数满足下式，则称为三角模糊数．其中，α，β分别为三角模糊数的左、右宽度，且α>0,β>0，c为三角模糊数的中心，如果左、右宽度相等，则称为对称三角模糊数，记为
其隶属度函数如下，相应的函数图形如图2所示：
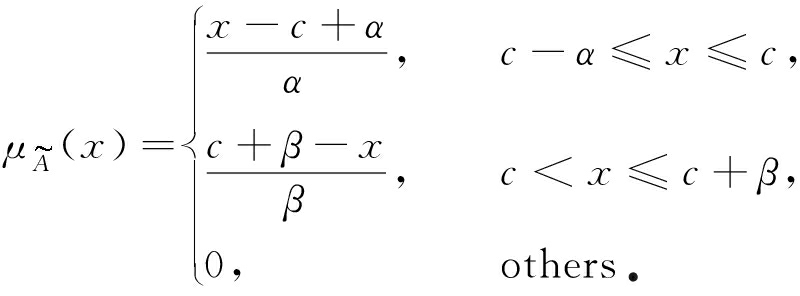
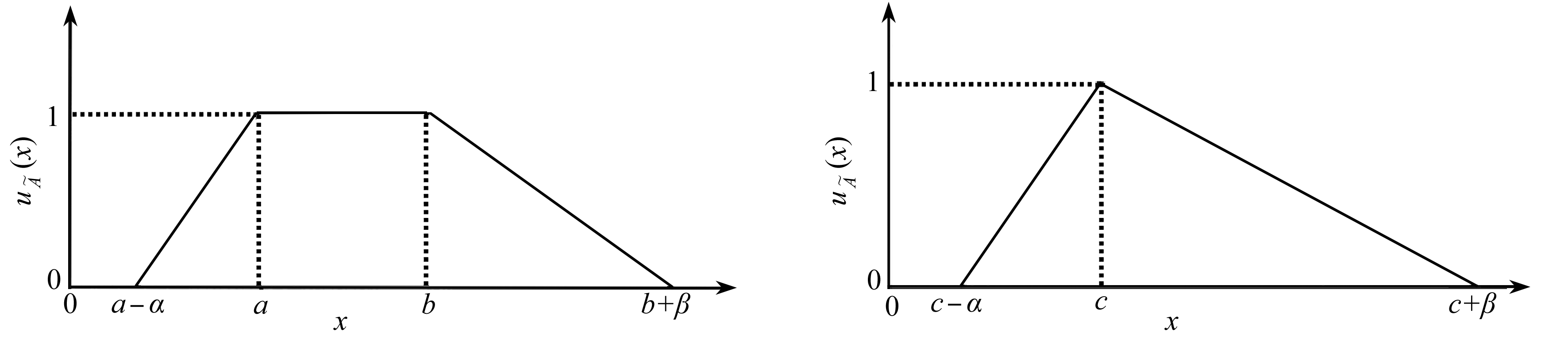
图1 梯形模糊数 图2 三角模糊数
Fig. 1 The trapezoidal fuzzy number Fig. 2 The triangular fuzzy number
定义6[16] 当是三角模糊数时，的上、下可能性均值分别为式(1)、(2)，则三角模糊数的清晰可能性均值为式(3)：
(1)
(2)
(3)
定义7[16] 当是梯形模糊数时，的上、下可能性均值分别为式(4)、(5)，则梯形模糊数的清晰可能性均值为式(6)：
(4)
(5)
(6)
定理1[17] 设ε是固定可能性分布下的梯形模糊变量(r1,r2,r3,r4)，且4个参数的大小关系为r1<r2<r3<r4．那么它的二阶矩为
(7)
其中n为模糊变量的个数.
定理2[17] 设ε是固定可能性分布下的三角模糊变量(r1,r2,r3)，其中r1<r2<r3，那么其二阶矩为
(r3-r2)(3r1-2r2-r3)3-(2r2-r1-r3)4]，
(8)
其中n为模糊变量的个数.
定理3[17] 设投资收益εi=(ri1,ri2,ri3,ri4)(i=1,2,3,…,n)是固定可能性分布下的相互独立的梯形模糊变量且构成的参数矩阵为
(9)
式(9)满足行满秩，那么二阶矩M2[ε]是决策向量x的二次凸函数，则二阶矩M2[ε]可等价表示为式(10)，其中D为半正定矩阵：
(10)
D=[5 1 -3 -3; 1 5 -3 -3; -3 -3 5 1; -3 -3 1 5].
2 考虑交易费用和背景风险的模糊投资组合选择模型
假设对n个风险资产和1个无风险资产进行投资，风险资产i的收益率ξi为梯形模糊数，xi(i=1,2,3,…,n)是风险资产i的投资比例，ξ0是无风险资产的利率，背景风险
的收益率为对称三角模糊数，由定义4和定义5计算出第i种风险资产的可能性均值、背景风险收益率的可能性均值和投资组合的收益分别如下：
(11)
(12)
(13)
式(13)中ki表示风险资产i的交易费用，
表示资产i初期的投资比例．由定义4和定义5可以计算出投资组合收益率的可能性均值为
(14)
本文采用模糊收益与其期望值的二次偏差，即模糊收益率的二阶矩M2[R]表示投资组合的风险．由式(10)可知，风险资产的二阶矩为M2[ε]=(1/48)xTSTDSx，背景风险的二阶矩为
则投资组合的风险函数可表示为式(15)．将换手率用于度量证券的流动性，由于证券流动性的大小往往与主观意愿有关，故将其作为模糊现象进行处理，假设风险资产i的模糊换手率为梯形模糊数：li=(lai,lbi,lαi,lβi)，由式(4)～(6)可知，资产i(i=1,2,3,…,n)的模糊换手率的可能性均值为
则投资组合x=(x1,x2,…,xn)的模糊换手率的可能性均值可表示为式(16)：
(15)
(16)
综合上述相关计算，建立以投资组合的风险，即二阶矩函数为目标函数，预设收益率、换手率的可能性均值要求水平以及风险资产的投资比例为约束条件的模糊投资组合模型，并要求在满足相应约束条件下，投资组合风险最小化．模型的数学形式如下所示：
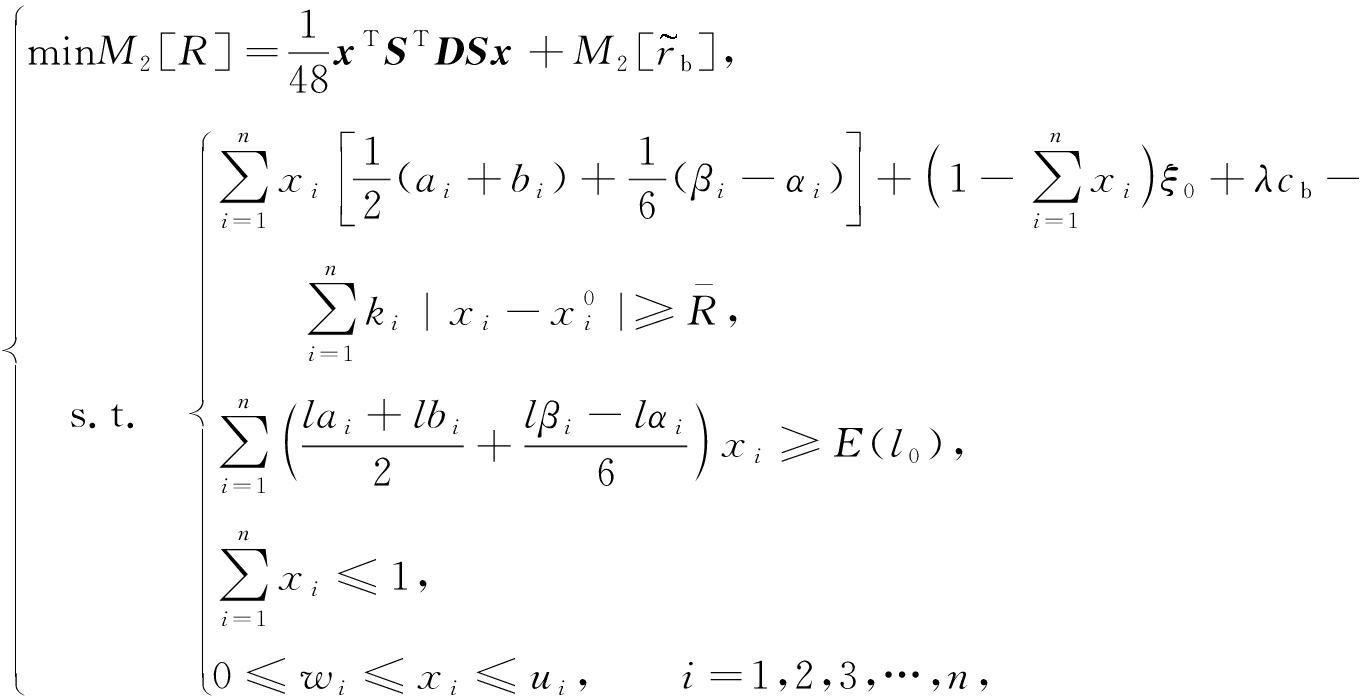
(17)
其中S为固定可能性分布下投资收益构成的参数矩阵,D为半正定矩阵，D=[5 1 -3 -3; 1 5 -3 -3; -3 -3 5 1; -3 -3 1 5],[ai,bi]和[lai,lbi]分别为风险资产i的收益率以及换手率的容许区间，[αi,βi]和[lαi,lβi]分别为收益率和换手率的左右宽度，λ为背景风险对投资组合收益率的影响因子，ki为风险资产的交易费用的比例系数，
为风险资产i期初的持有比例，
为预先给定的期望收益率，E(l0)为投资者对投资组合模糊换手率可能性均值的要求水平，wi，ui分别表示资产i投资比例的下界和上界.
3 数值计算与分析
本文选取中证100指数成分股中5支热门股票：贵州茅台(600519)、兴业银行(601166)、格力电器(000651)、美的集团(000333)、中国平安(601318)为分析对象，选取这5支股票2019年第一季度(2019年1月2日至2019年3月29日)所有交易日数据作为实证研究的基础数据，股票的收益率和换手率均为梯形模糊数．用客观模糊频数统计近似估计梯形模糊数的相关参数．下面以贵州茅台(600519)为例，具体方法为：计算该股票第一季度的日收益率，并给出收益率的频数分布图，如图3所示．从图3中可以看出，收益率集中在0.16～0.21和0.26～0.31，首先计算0.16～0.21间历史收益率的均值为0.193，并将其作为容许区间的左端点；然后计算0.26～0.31间历史收益率的均值为0.287，将其作为容许区间的右端点；将历史收益率按升序排列，选择0.06～0.11区间的第3个交易日的收益率0.042作为最小可能值，并将0.31～0.36区间的第2个交易日的历史收益率0.323作为最大可能值， 于是得到左宽度为0.086， 右宽度为0.061， 最后得到贵州茅台的梯形模糊数为(0.193,0.287,0.086,0.061)．为了便于求解，将梯形模糊数的最小可能值、 左端点、 右端点、 最大可能值依次作为固定可能性分布下的梯形模糊变量的4个参数值， 则贵州茅台固定可能性分布下的梯形模糊变量为(0.042,0.193,0.287,0.323).
图3 贵州茅台收益率频数分布图
Fig. 3 The frequency distribution map of the return rate of Kweichow Moutai
基于以上客观模糊频数统计近似估计方法的介绍，对证券收益率和换手率的模糊数参数估计和固定可能性分布下的梯形变量参数估计，均采用此方法进行相关参数的估计，分别统计计算出5支股票第一季度的收益率以及交易日的换手率，按照上述方法同理可得到5支股票收益率和换手率为梯形模糊数和固定可能性分布下的梯形模糊变量的参数分布，如表1所示．其中R(a,b,α,β)表示收益率为梯形模糊数的参数，R(r1,r2,r3,r4)表示收益率为固定可能性分布下的梯形模糊变量参数，L(a,b,α,β)表示换手率为梯形模糊数的相关参数，L(r1,r2,r3,r4)表示换手率为固定可能性分布下的梯形模糊变量参数.
表1 选取的5支股票模糊收益率和模糊换手率
Table 1 The fuzzy return rate and the fuzzy turnover rate of 5 selected stocks
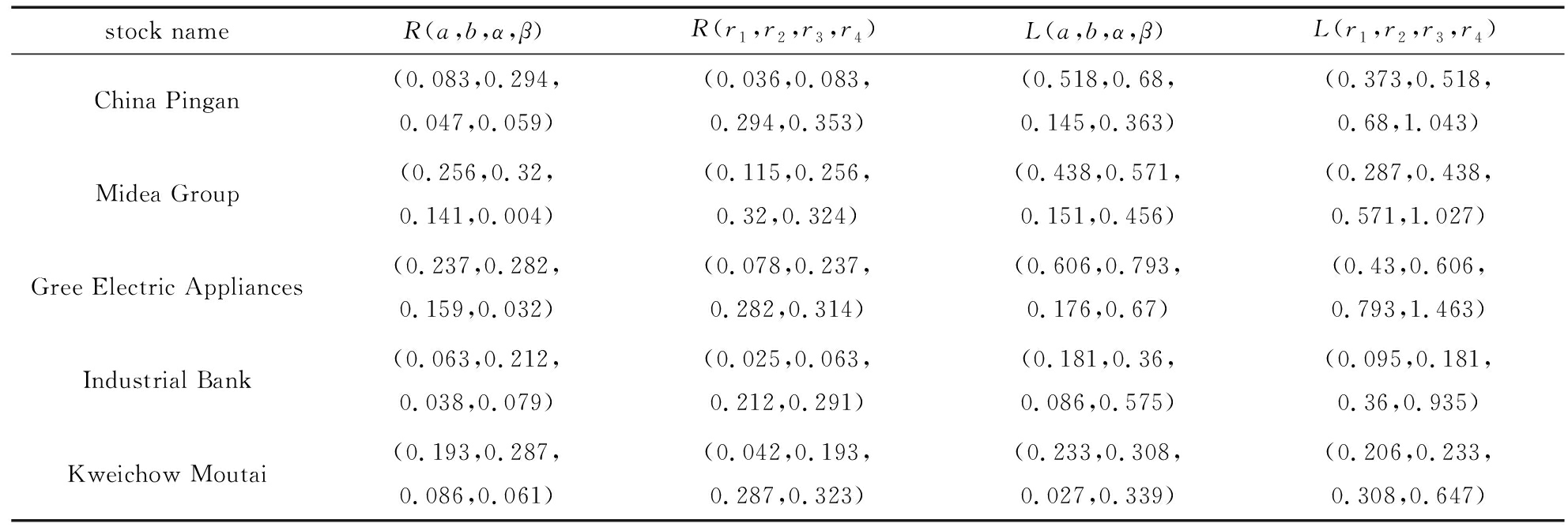
stock nameR(a,b,α,β)R(r1,r2,r3,r4)L(a,b,α,β)L(r1,r2,r3,r4)China Pingan(0.083,0.294,0.047,0.059)(0.036,0.083,0.294,0.353)(0.518,0.68,0.145,0.363)(0.373,0.518,0.68,1.043)Midea Group(0.256,0.32,0.141,0.004)(0.115,0.256,0.32,0.324)(0.438,0.571,0.151,0.456)(0.287,0.438,0.571,1.027)Gree Electric Appliances(0.237,0.282,0.159,0.032)(0.078,0.237,0.282,0.314)(0.606,0.793,0.176,0.67)(0.43,0.606,0.793,1.463)Industrial Bank(0.063,0.212,0.038,0.079)(0.025,0.063,0.212,0.291)(0.181,0.36,0.086,0.575)(0.095,0.181,0.36,0.935)Kweichow Moutai(0.193,0.287,0.086,0.061)(0.042,0.193,0.287,0.323)(0.233,0.308,0.027,0.339)(0.206,0.233,0.308,0.647)
本文将三个月定期存款作为无风险资产，年收益率为1.35%，月平均收益率为0.112 5%，交易费用ki=0.005．假设投资者初期拥有的资产比例为0，投资比例的下界限制为wi=0，上界限制为ui=0.8，λ=0.1．假设背景风险
的对称三角模糊数收益率为(0.8,0.2)，即固定可能性分布下三角模糊变量为(0.6,0.8,1)．设定期望收益率
分别计算这5支热门股票的平均换手率，再分别将其均值进行等比例加权平均，进而假设投资者对投资组合模糊换手率可能性均值的要求水平E(l0)=0.5．用MATLAB遗传算法进行求解， 得出在此期望收益率下， 对5支股票的投资比例为(0.102,0.127,0.672,0,0.099)时， 达到投资组合风险最小0.014，并调用绘图函数，绘制了最佳适应度值(best fitness)、最佳个体(best individual)、个体间平均距离(distance)以及期望(expectation)在个体进化过程中的变化情况，如图4所示，图形的变化说明了种群规模对算法性能产生了积极的影响.
图4 遗传过程个体的变化情况
Fig. 4 Individual changes in genetic processes
将预设投资收益率设置为0.23时，所得到的最优投资方案为(0.102,0.127,0.672,0,0.099)，即主要将资产分配在中国平安、美的集团和格力电器这三种证券上，不对或者较少地对兴业银行和贵州茅台投资，以期实现该预期收益下的风险最小，即模糊投资组合风险为0.014．将预设的期望收益控制在0.2～0.26之间，计算出不同预设期望收益率下资产投资比例和投资组合风险的变化，最终该模糊投资组合模型式(17)对应的有效投资组合如表2所示．由此可见，在投资者预设不同的期望收益率时，对各风险资产的分配也不尽相同．随着预期收益率的变化，对美的集团和贵州茅台的投资比例变动较大，这说明模型(17)在计算投资组合风险时，综合考虑了证券收益率和流动率对投资风险的影响．从表2还可以看出，对兴业银行的投资比例始终为0，说明兴业银行的平均收益率和平均换手率都比较低，即兴业银行证券的流动性较差.
表2 不同期望收益率下的有效投资组合
Table 2 Effective portfolio with different expected return
R-portfolio riskChina PinganMidea GroupGree Electric AppliancesIndustrial BankKweichow Moutai0.20.013 60.11200.800.0880.210.013 80.2250.0950.67800.0030.220.013 90.0790.1970.724000.230.0140.1020.1270.67200.0990.240.014 20.20200.54600.2520.250.014 40.2030.3660.37700.0550.260.014 50.0920.1460.76200
从表2中可以直观地看出，逐渐增加对投资组合期望收益的设定，随着期望收益的增大，投资风险也会相应增加，投资组合风险和收益的相关关系如图5所示．从图5中可以看出，模型式(17)的数值分析符合“高收益、高风险”的一般规律，验证了模型的有效性，因此说明考虑背景风险和流动性的模糊投资组合模型能较好地反应现实经济中的投资收益和风险的关系.
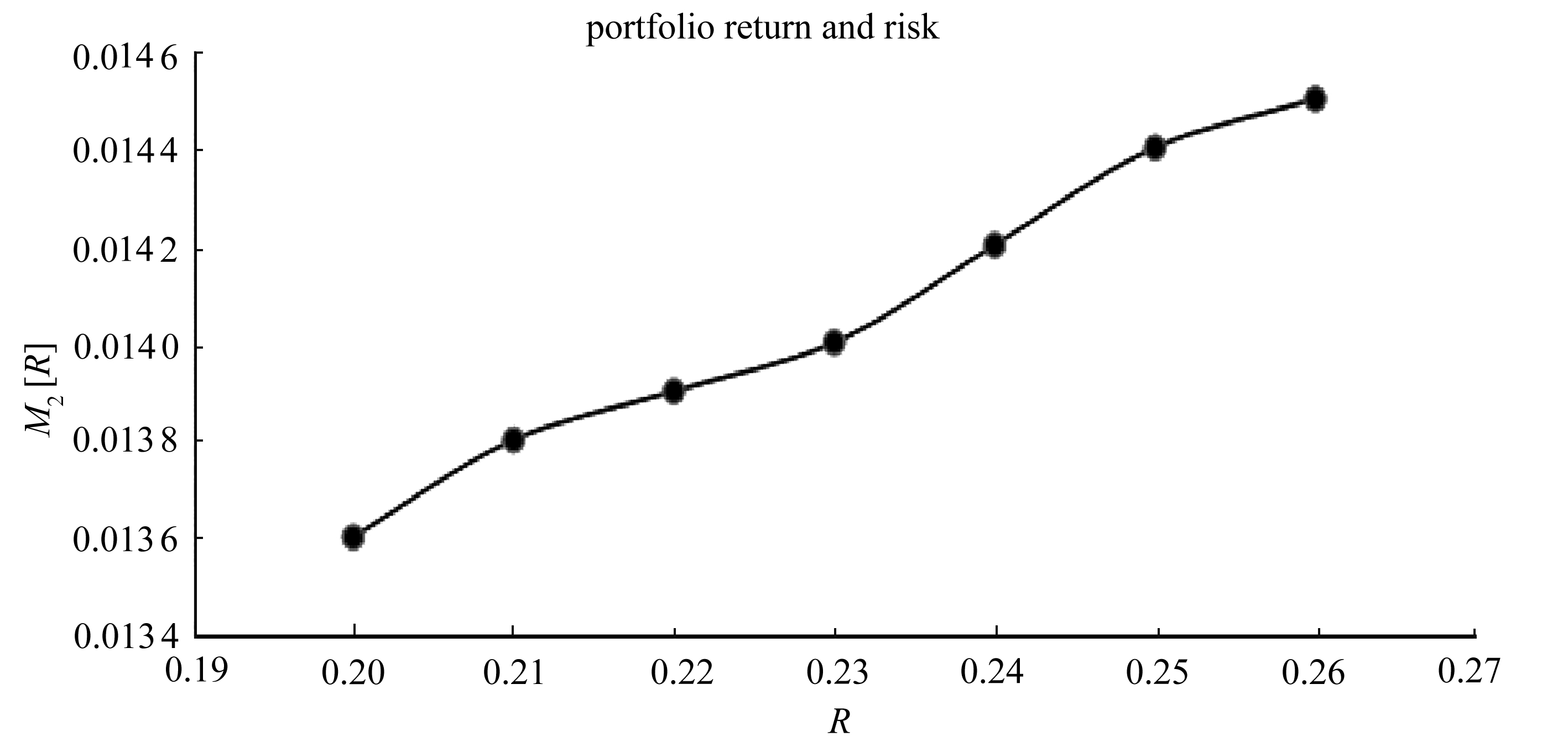
图5 投资收益与风险的关系
Fig. 5 The relation between portfolio return and risk
4 总 结
本文提出了一个考虑背景风险和流动性的模糊投资组合模型．将影响投资者决策的背景风险和证券换手率作为模型相应的约束条件，并用投资收益率的二阶矩作为投资组合风险度量函数，建立了要求投资组合风险最小的模糊投资组合模型．然后，选取真实市场的部分股票数据对模型进行验证，计算出不同期望收益率下的投资组合风险和各风险资产的投资比例，其计算结果符合“高收益、高风险”的一般规律，验证了考虑背景风险和收益率的模糊投资组合模型的有效性，也说明该模型能反映现实金融市场，为投资者提供了一定的参考.
本文的创新点具有以下几个方面：
1) 考虑了背景风险，并将其收益率作为对称三角模糊数，既全面分析了投资者面临的风险，又简化了模型计算；
2) 考虑了用换手率度量证券流动性，反映资金进出市场的情况；
3) 不同于一般的均值-方差模糊投资组合，本文将收益率的二阶矩作为风险的度量函数，模糊变量的二阶矩具有凸性，更有利于找到全局最优解；
4) 本文用客观模糊频数统计近似估计，梯形模糊数和固定可能性分布下的模糊变量的相关参数，具有一定的科学性.
[1] MARKOWITZ H. Portfolio Selection: Efficient Diversification of Investments[M]. New York: Wiley, 1959.
[2] ARNOTT R D, WAGNER W H. The measurement and control of trading costs[J]. Financial Analysis Journal, 1990, 46(6): 73-80.
[3] MORTON A J, PLISKA S R. Optimal portfolio management with fixed transaction costs[J]. Mathematical Finance, 1995, 5(4): 337-336.
[4] HUANG X X, YANG T T. How does background risk affect portfolio choice: an analysis based on uncertain mean-variance model with background risk[J]. Journal of Banking and Finance, 2020, 111: 105726.
[5] HEATON J, LUCAS D. Market frictions, savings behavior, and portfolio choice[J]. Macroeconomic Dynamics, 1997, 1(1): 76-101.
[6] 李佳, 徐维军, 张卫国. 含有背景风险的双目标投资组合模型研究[J]. 运筹与管理, 2017, 26(4): 118-123.(LI Jia, XU Weijun, ZHANG Weiguo. Bi objective portfolio selection model and algorithm with background risk[J]. Operations Research and Management Science, 2017, 26(4): 118-123.(in Chinese))
[7] 玄海燕, 金珍, 张玉春, 等. 基于背景风险的个人投资者投资决策研究[J]. 重庆师范大学学报(自然科学版), 2019, 36(4): 93-99.(XUAN Haiyan, JIN Zhen, ZHANG Yuchun, et al. Research on investment decision of individual investors based on background risk[J]. Journal of Chongqing Normal University(Natural Sciences), 2019, 36(4): 93-99.(in Chinese))
[8] DUBOIS D, PRADE H. Possibility Theory: an Approach to Computerized Processing of Uncertainty[M]. Springer, 1988.
[9] CARLSSON C, FULLER R. On possibilistic mean value and variance of fuzzy numbers[J]. Fuzzy Sets and Systems, 2001, 122(2): 315-326.
[10] ZHANG W G, XIAO W L, XU W J. A possibilistic portfolio adjusting model with new added assets[J]. Economic Modelling, 2010, 27(1): 208-213.
[11] 李婷, 张卫国, 徐维军. 考虑背景风险因素的模糊投资组合选择模型[J]. 系统工程理论与实践, 2012, 30(12): 33-38.(LI Ting, ZHANG Weiguo, XU Weijun. Fuzzy portfolio selection model considering background risk[J]. Theory and Practice of System Engineering, 2012, 30(12): 33-38.(in Chinese))
[12] 邓雄, 徐维军, 李佳, 等. 基于背景风险和弹性增量的模糊投资组合研究[J]. 数学的实践与认识, 2016, 46(1): 38-46.(DENG Xiong, XU Weijun, LI Jia, et al. Research on fuzzy portfolio based on the background risk and elastic increment[J]. Practice and Understanding of Mathematics, 2016, 46(1): 38-46.(in Chinese))
[13] 李佳, 邓雄, 徐维军. 基于最大期望满意度与背景风险的模糊投资组合模型研究[J]. 数学的实践与认识, 2016, 46(15): 140-149.(LI Jia, DENG Xiong, XU Weijun. Research on fuzzy portfolio model based on maximum expectation satisfaction and background risk[J]. Practice and Understanding of Mathematics, 2016, 46(15): 140-149.(in Chinese))
[14] 刘俊卿, 韩晶. 基于模糊数学理论的沥青路面结构可靠度分析[J]. 应用数学和力学, 2018, 39(9): 1081-1090.(LIU Junqing, HAN Jing. Reliability analysis of asphalt pavement structure based on fuzzy mathematics theory[J]. Applied Mathematics and Mechanics, 2018, 39(9): 1081-1090.(in Chinese))
[15] 方勇, 汪寿阳. 模糊投资组合优化: 理论与方法[M]. 北京: 高等教育出版社, 2005.(FANG Yong, WANG Shouyang. Fuzzy Portfolio Optimization: Theory and Method[M]. Beijing: Higher Education Press, 2005.(in Chinese))
[16] 陈国华, 陈收, 方勇, 等. 带有模糊收益率的投资组合选择模型[J]. 系统工程理论与实践, 2009, 29(7): 8-15.(CHEN Guohua, CHEN Shou, FANG Yong, et al. Portfolio selection model with fuzzy return[J]. Theory and Practice of System Engineering, 2009, 29(7): 8-15.(in Chinese))
[17] 刘彦奎, 白雪洁, 杨凯. 参数可信性优化方法[M]. 北京: 科学出版社, 2017.(LIU Yankui, BAI Xuejie, YANG Kai. Parameter Credibility Optimization Method[M]. Beijing: Science Press, 2017.(in Chinese))