引 言
反应扩散方程是一类特殊的非线性波方程,它在不同科学领域对各种非线性现象的定性描述中起着重要作用[1],是非线性科学研究中的一个热点问题.现实世界中大量的实际问题能够与反应扩散方程相联系,例如传热传质、流体力学、土壤湿度、病毒生长、生物种群等.反应扩散方程包括反应项和扩散项,其典型的形式如下:
(1)
其中u=u(x,t)表示关于x∈Rn和t∈R的密度或浓度.方程(1)等号右边的第一项描述的是扩散项,对∀u≥0,扩散函数D(u)满足D(u)>0;等号右边第二项是反应项.近年来,对于非线性波方程的孤立周期波的研究吸引了许多学者的兴趣.文献[2]研究了一类广义BBM方程的孤立波和周期波的存在性问题.文献[3]给出了一类奇异摄动高阶KdV方程的孤立波解.文献[4]讨论了细菌生长的反应扩散模型行波解的存在性且得到了一个近似解.文献[5]探索了振荡反应中周期行波发生的条件以及波的稳定性.
方程(1)的一个行波是形如u(x,t)=φ(x-ct)=φ(ξ)的解,其中c为波速,ξ=x-ct.一个周期波列是对应周期函数φ的行波.众所周知,许多非线性波方程可以通过行波变换转换为平面动力系统(行波系统),从而能够运用微分方程的定性理论和分支理论去研究.经典的研究方法可参阅文献[6].将u(x,t)=φ(x-ct)=φ(ξ)代入方程(1),可得
(2)
这里![]() 令v
令v![]()
![]() 及做尺度变换dξ/dτ=D(φ),系统(2)等价于下列平面动力系统(行波系统):
及做尺度变换dξ/dτ=D(φ),系统(2)等价于下列平面动力系统(行波系统):
(3)
在系统(3)的奇点是中心的情况下,会有连续的周期波列(周期行波解)展开于方程(1)的均匀稳态解[7].如果系统(3)在奇点的邻域出现m个极限环,那么会有m个孤立周期行波或孤立周期波列接近系统(1)的稳态解[7-8].我们可以通过研究中心类型奇点周期轨道的性质,从而了解围绕对应稳态解的连续周期波列的情况.文献[7]研究了一类含有常数扩散项和三次反应项的反应扩散方程,获得从稳态解最多能分支出4个小振幅孤立周期波(SAIPW)的结果.文献[8]中讨论了一类含有常数扩散项和四次反应项的反应扩散方程的情形.更多关于行波方程的周期行波和Hopf分支的研究可查看文献[9-10].此外,与中心和极限环紧密联系的一个重要领域是微分系统的局部临界周期.在1989年,文献[11]通过类比Bautin研究极限环的方法,首次引入细中心和局部临界周期分支的概念,建立了局部临界周期分支理论,且研究了二次系统的局部临界周期分支.对于从系统的细中心最多能分支出几个局部临界周期的问题,一些经典系统已经被研究且获得一些成果.对于线性中心经三次齐次非线性扰动的临界周期分支问题已经被解决[12].三次Kukles系统[13]、可逆三次系统[14]和四次Kukles系统[8]的临界周期分支问题也得到了解决.在文献[8]中,笔者用临界周期分支的方法讨论了一类反应扩散方程的周期波解和周期波长问题.
国内外学者对反应扩散方程的研究已经取得了一些成果,但对含更高次反应项的反应扩散方程和利用极限环理论去研究还较少.本文受到文献[8]的启发,考虑下述一类含有常数扩散项和五次反应项的反应扩散方程的SAIPW和局部临界周期波长问题:
(4)
这里u=u(x,t), fi, j∈R,d>0,λ![]() (d, f01,…, f14, f05).
(d, f01,…, f14, f05).
本文的结构如下:第1节给出一些必要的基础知识和结果.第2节首先运用行波变换将非线性波方程转换为对应的行波系统;然后利用奇点量方法计算出该系统的前几阶奇点量,探索该系统奇点的中心条件;证明了行波系统原点处能分支出的极限环最大个数,即对应的非线性反应扩散方程存在SAIPW解最多个数.第3节借助周期常数的计算,研究行波系统原点的细中心阶数,并证明该系统最多能分支出的局部临界周期个数;而后再通过分析行波系统的临界周期分支得到对应反应扩散方程有多少个临界周期波长.第4节给出本文的结论和展望.
1 预 备 知 识
考虑如下实多项式微分系统:
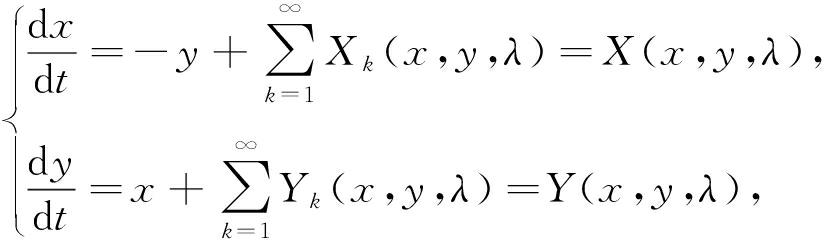
(5)
其中λ∈Λ,Λ是参数集.假设函数X(x,y,λ)和Y(x,y,λ)在原点的邻域内解析且原点是系统(5)的中心型奇点.利用变换![]() 微分系统(5)可转换为复系统:
微分系统(5)可转换为复系统:
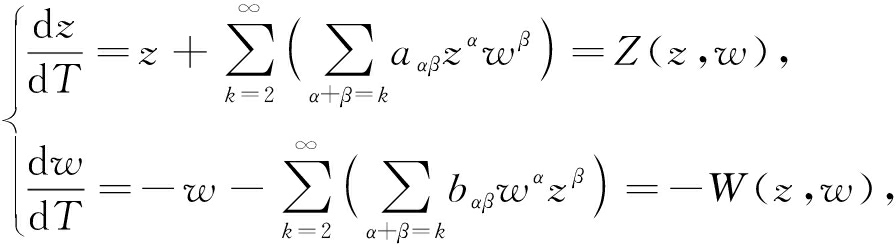
(6)
注意,系统(6)的系数是有共轭关系的,即![]() 我们称系统(6)是实系统(5)的伴随复系统[15].
我们称系统(6)是实系统(5)的伴随复系统[15].
对充分小的h,设P(h,λ)为系统(5)通过非零点(h,0)的闭轨的最小周期函数.文献[11]给出了周期函数P(h,λ)的表达式:
(7)
P2k称为系统(5)原点的第k阶周期常数.
定义1[11] 若存在k∈N,λ*∈Λ,使得P2(λ*)=P4(λ*)=…=P2k(λ*)=0,P2k+2(λ*)≠0,则称系统(5)的原点为对参数λ*的k阶细中心.若k=0,则原点是粗中心;若对∀k∈N,都有P2k(λ*)=0,则原点是等时中心.
定义2[11] 考虑有限函数族fj:RN→R, j=1,2,…,k.实(复)代数簇V(f1, f2,…, fk)定义为λ∈RN (CN)的集合,使得fj(λ)=0, j=1,2,…,k.对f:RN→R,如果
1) λ*∈RN的任一邻域包含有λ∈V(f1, f2,…, fk-1),使得fk(λ)f(λ)<0;
2) 代数簇V(f1, f2,…, fj),2≤j≤k-1,若λ∈V(f1, f2,…, fj)且fj+1(λ)≠0,则λ的任一邻域W包含有σ∈V(f1, f2,…, fj-1),使得fj(σ)fj+1(λ)<0;
3) 若λ∈V(f1)且f2(λ)≠0,则λ的任一开邻域包含一个σ,使得f1(σ)f2(λ)<0.
那么就说f1, f2,…, fk在λ*∈V(f1, f2,…, fk)关于f是无关的.
引理1[11] 若参数λ=λ*时,系统(5)的中心O是k阶细中心,则至多有k个临界周期从中心O分支出来.进一步地,如果周期常数P2,P4,…,P2k在λ*关于P2k+2是无关的,那么恰有m(m≤k)个临界周期从中心O分支出来.
由文献[16]中定理5.4可知,系统(5)原点的第一个非零周期常数P2k和系统(6)原点的第一个非零复周期常数τk满足以下关系:
P2k=-πτk.
(8)
计算系统(6)原点的复周期常数τk的详细方法见文献[17].
假设复周期常数τi取决于k个独立参数a1,a2,…,ak,即τi=τi(λ)=τi(a1,a2,…,ak).由等式(8)以及文献[18]中定理2, 我们有下述用于证明系统奇点存在局部临界周期的充分性引理.
引理2 [18] 对于系统(6)的原点,若存在λ*=(a1c,a2c,…,akc),使得
(9)
则通过对λ*的小扰动,系统(6)恰好有k个局部临界周期从原点分支出来.
2 奇点量、连续周期波列和SAIPW
在这一节中,我们将主要探索反应扩散方程(4)稳态解u(x,t)≡α的周期波列的性质,这一目标可通过研究方程(4)对应的行波系统细焦点(α,0)的性质来实现.通过计算行波系统的伴随复系统的前几阶奇点量,寻找系统奇点的中心条件以及最大SAIPW个数.
![]() 受到文献[9]的启发,提出了下述假设.这一假设构建了类型(1)非线性波方程的稳态解和对应行波系统的细焦点之间的桥梁,也是研究类型(1)非线性波方程行波解存在性的重要途径.
受到文献[9]的启发,提出了下述假设.这一假设构建了类型(1)非线性波方程的稳态解和对应行波系统的细焦点之间的桥梁,也是研究类型(1)非线性波方程行波解存在性的重要途径.
假设1 方程(1)中的扩散函数D(u)和反应项f(u,ux)满足以下条件:
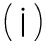 f(0,0)=f(1,0)=0,f(α,0)=0,对∀α∈(0,1);否则,f(u,0)≠0.
f(0,0)=f(1,0)=0,f(α,0)=0,对∀α∈(0,1);否则,f(u,0)≠0.
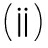 f(φ,v)∈Cω(R2),fφ(0,0)<0,fφ(α,0)>0且fφ(1,0)<0.
f(φ,v)∈Cω(R2),fφ(0,0)<0,fφ(α,0)>0且fφ(1,0)<0.
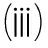 D(u)∈Cω(R),对∀u≥0,有D(u)>0.
D(u)∈Cω(R),对∀u≥0,有D(u)>0.
显然,在上述假设条件之下,点p0(0,0),p1(1,0)和pα(α,0)是系统(3)对应于方程(1)的稳态解的奇点,此外没有其他奇点.
我们记DX(φ*,0)为行波系统(3)在奇点(φ*,0)的线性化系统的系数矩阵,λspec(DX(φ*,0))为矩阵DX(φ*,0)的特征值,它们的表达式如下:
其中γφ*=-c-fv(φ*,0),Δφ*=(c+fv(φ*,0))2-4D(φ*)fφ(φ*,0).将假设1的条件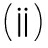 和
和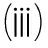 代入以上表达式计算可知,p0,p1是系统(3)的双曲鞍点.若Δα≥0,则pα是结点;若Δα<0且γα≠0,则pα是焦点.以上两种情况中,pα的稳定性由γα的符号决定.若γα=0,即当c=-fv(α,0)时,此时Δα<0,故λspec(DX(pα))∈iR;在这种情况下,pα是细焦点且从方程(1)的稳态解u(x,t)≡α可能分支出SAIPW [7].
代入以上表达式计算可知,p0,p1是系统(3)的双曲鞍点.若Δα≥0,则pα是结点;若Δα<0且γα≠0,则pα是焦点.以上两种情况中,pα的稳定性由γα的符号决定.若γα=0,即当c=-fv(α,0)时,此时Δα<0,故λspec(DX(pα))∈iR;在这种情况下,pα是细焦点且从方程(1)的稳态解u(x,t)≡α可能分支出SAIPW [7].
在下面的讨论中,除了特别说明之外,总是限制D(u)为常数,即方程(1)包含常数扩散项的情况.考虑如下含有五次反应项f(u,ux)的反应扩散方程:
(10)
其中d>0, fij∈R.令f10<0, f20=-f10(α+1)/α, f30=f10/α, f40=f50=0,α∈(0,1),显然,方程(10)满足假设1的条件.方程(10)可转换为形如系统(3)的行波系统:

(11)
对于这个系统,我们计算得
其中
γα=-c-(f01+f11α+f21α2+f31α3+f41α4),
我们令c=c*=-(f01+f11α+f21α2+f31α3+f41α4),得γα=0,Δα=-4df10(α-1)<0,所以λspec(DX(α,0))∈iR.由此可知,(α,0)是细焦点且从稳态解u(x,t)≡α可能分支SAIPW.
对于方程(4),对照上面有α=1/2,下面我们讨论方程(4)在稳态解u(x,t)≡1/2的SAIPW分支.为了讨论方便,我们将方程(4)对应的行波系统奇点(1/2,0)平移到坐标原点且进行尺度变换,即令![]() 且
且![]() 可得到方程(4)对应的平面微分系统:
可得到方程(4)对应的平面微分系统:

(12)
对系统(12)做变换![]() 我们得到它的伴随复系统:
我们得到它的伴随复系统:
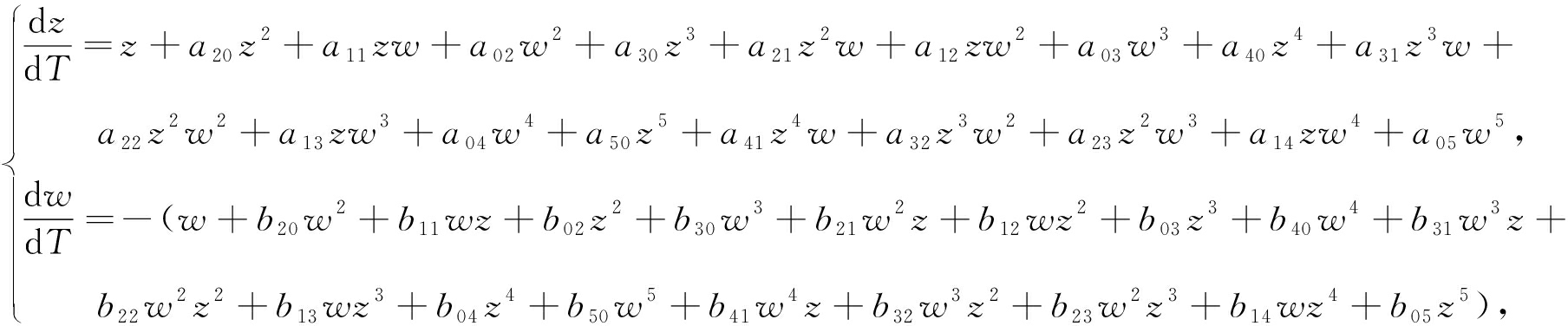
(13)
其中


通过计算复系统(13)原点的奇点量,再由实系统奇点的焦点量与伴随复系统奇点的奇点量之间的等价关系,可以确定从实系统(12)原点分支出的小振幅极限环个数,从而获得从方程(4)的稳态解u(x,t)≡1/2分支出的SAIPW数目.
运用文献[19]中定理2的递推公式进行仔细计算并分析计算结果,我们有以下定理.
定理1 复系统(13)的前8个奇点量全部为零,当且仅当满足下列条件之一:
K1={λ∈R9: f03=f05=f13=0};
K2={λ∈R9: 2f03+f13=0, f05=0, 2f04+f14=0, 2f02+f12=0}.
证明 必要性.将系统(13)的系数代入文献[19]中定理2的递推公式进行计算,可得![]() 令f03=-f13/2,得μ1=0且
令f03=-f13/2,得μ1=0且![]() 再令f05=6f13(2f02+f12)/5,得μ2=0且
再令f05=6f13(2f02+f12)/5,得μ2=0且![]() 取
取![]() 得μ3=0且
得μ3=0且
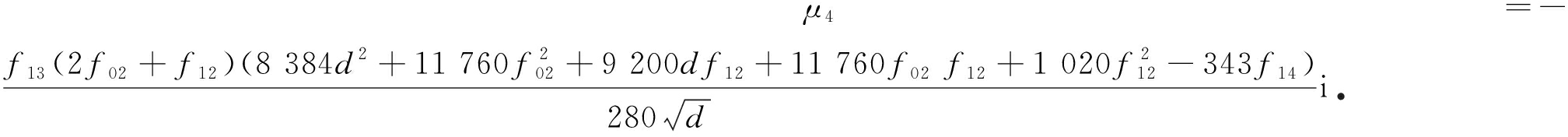
再取![]() 得μ4=0且
得μ4=0且
这里
F0=899 184 838 685 683 965 029 890 839 471 690 326 604 873 618 006 549
674 053 265 479 127 114 300 359 926 555 625 490 075 367 578 280d5/2,
F3和F4也为d, f02, f12的表达式,因其表达式较复杂,故在此省略.
若f13=0,则f05=f03=0且前8个奇点量全都为零.因此,我们得到条件K1.
若2f02+f12=0,则f04=-f14/2, f05=0, f03=-f13/2且前8个奇点量全都为零.因此,我们得到条件K2. 若f13(2f02+f12)≠0,不失一般性,我们取d=1,得
Res(F2,F3, f02)=M1,
Res(F2,F4, f02)=M2,
Res(M1,M2, f12)=50 096 392 356 781 803 791 886 937 692 913 903 439 852 161 558 375 638…,
其中,Res(Y1,Y2,x)是多项式Y1和Y2关于变量x的结式,M1和M2分别是f12的20次和28次幂多项式.因为Res(M1,M2, f12)≠0,所以M1=M2=0没有实根f12.所以,当f13(2f02+f12)≠0且d>0时,存在μ1=μ2=μ3=μ4=μ5=μ6=μ7=0,μ8≠0.因此,系统(13)的细奇点的最高阶数为8.
充分性.由必要性的证明过程容易看到,如果λ∈K1∪K2,那么
μ1=μ2=μ3=μ4=μ5=μ6=μ7=μ8=0.
由实系统(12)原点的焦点量与伴随复系统(13)原点的奇点量之间的等价关系,我们有以下定理.
定理2 实平面解析系统(12)的原点为中心点(系统(13)的原点为复中心点),或等价地说,非线性反应扩散方程(4)有连续的周期波列以恒定波速c=c*围绕稳态解u(x,t)≡1/2,当且仅当λ∈K1∪K2.
证明 当条件K1满足时,系统(12)可以写为

(14)
显然,系统(14)是关于x轴对称的.因此,若条件K1满足,则系统(12)的原点是一个中心点.
当条件K2满足时,系统(12)变为
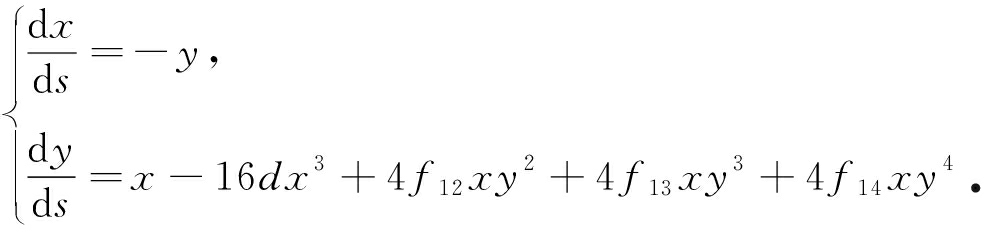
(15)
显然,系统(15)是关于y轴对称的.因此,若条件K2满足,则系统(12)的原点是一个中心点.
由定理1的证明过程,我们可得到以下结果.
定理3 系统(13)的原点是一个8阶细奇点(系统(12)的原点是一个8阶细焦点),当且仅当

(16)
接下来,不失一般性,我们假设d=1.通过解方程F1=F2=F3=0,可得到它的8个实数解,其中一个解可表示为

(17)
经过仔细地计算,我们得到下面的Jacobi行列式:
根据文献[14]中定理2以及焦点量和奇点量的等价关系[15],通过对参数λ=(d, f01,…, f14, f05)的临界值进行适当的扰动,使得从系统(12)的原点恰好能分支出8个小振幅极限环.由文献[7],我们得到本节的主要结果.
定理4 若非线性反应扩散方程(4)满足条件f10<0, f20=-f10(α+1)/α, f30=f10/α,则从方程(4)的稳态解u(x,t)≡1/2最多能分支出8个SAIPW.另外,存在参数值λ*,使得从非线性反应扩散方程(4)的稳态解u(x,t)≡1/2恰好能分支出8个SAIPW.
3 细中心和局部临界周期分支
由文献[20],我们得到非线性方程(1)的连续周期波列φ的波长等价于系统(3)原点O的周期函数P(h,λ).如果系统(3)原点O存在m个临界周期分支,则方程(1)的连续周期波列的波长的单调性发生m次变化,我们也称方程(1)具有m个临界周期波长.通过变换![]() 所以系统(4)在u(x,t)≡1/2附近的周期波列波长的单调性与系统(12)原点附近的周期轨的周期函数的单调性一致.由本文中的定理2我们知道,如果λ∈K1∪K2,那么系统(12)的原点为中心点.在此基础上,我们将继续讨论系统(12)的细中心和局部临界周期分支问题,分别考虑下述两种情形.
所以系统(4)在u(x,t)≡1/2附近的周期波列波长的单调性与系统(12)原点附近的周期轨的周期函数的单调性一致.由本文中的定理2我们知道,如果λ∈K1∪K2,那么系统(12)的原点为中心点.在此基础上,我们将继续讨论系统(12)的细中心和局部临界周期分支问题,分别考虑下述两种情形.
情形K1 f03=f05=f13=0.
我们将定理1的条件K1代入文献[17]中的定理3.1的递推公式进行仔细地计算.若f12=0,我们有![]() 此时τ1≠0,则系统(13)的原点是粗中心.若f12≠0,我们得到系统(13)原点的前两个复周期常数:
此时τ1≠0,则系统(13)的原点是粗中心.若f12≠0,我们得到系统(13)原点的前两个复周期常数:
其中
若f02=-f12/2,我们有τ1=f12-12d,令f12=12d,得τ1=0且τ2=(f14-192d2)/2.取f14=192d2,得τ2=0且![]() 不失一般性,我们假设d=1,容易发现
不失一般性,我们假设d=1,容易发现![]() 没有实数解, 故对d>0, 有τ1=τ2=0, τ3≠0.因此, 系统(13)的原点是至多2阶的细中心.若f02≠-f12/2,令
没有实数解, 故对d>0, 有τ1=τ2=0, τ3≠0.因此, 系统(13)的原点是至多2阶的细中心.若f02≠-f12/2,令
![]() f14-135df12 f14-12f02 f12
f14-135df12 f14-12f02 f12 ![]() f14)/(288d(2f02+f12)),
f14)/(288d(2f02+f12)),
(18)
得τ2=0.如果f14=0,我们有
这里
不失一般性,假设d=1,我们有
G1=Res(H1,H3, f02)=
20 615 156 961 164 666 018 463 744-9 642 662 634 659 388 504 145 920 f12+
经过计算,我们发现G1=0没有实数解.因此,没有实数解满足方程H1=H3=0.故对d>0,有τ1=τ2=0,τ3≠0,所以,系统(13)的原点是至多2阶的细中心.若f14≠0,我们有
这里
不失一般性,假设d=1, f14=1,我们有
G2=Res(H1,H4, f02)=
334 087 967 779 619 575 729 383 014 400-156 526 967 543 031 197 868 648 038 400 f12+
经过计算,我们发现G2=0没有实数解.因此,没有实数解满足方程H1=H4=0.故对d>0,有τ1=τ2=0,τ3≠0,所以,系统(13)的原点是至多2阶的细中心.
由以上讨论过程,我们得到以下结果.
定理5 若λ*∈K1,则系统(13)的原点是一个阶数最大为2的细中心.此外,系统(13)原点是m(m=0,1,2)阶细中心,当且仅当![]() 其中
其中
![]() R9: f03=f05=f13=0,H1≠0},
R9: f03=f05=f13=0,H1≠0},
![]() R9: f03=f05=f13=0,H1=0,H2≠0},
R9: f03=f05=f13=0,H1=0,H2≠0},
![]() R9: f03=f05=f13=0,H1=0,H2=0}.
R9: f03=f05=f13=0,H1=0,H2=0}.
由上述定理,我们有以下结论.
定理6 对于参数λ*,若![]() 系统(13)没有局部临界周期从原点分支出来;若
系统(13)没有局部临界周期从原点分支出来;若![]() 系统(13)至多有m个局部临界周期从原点分支出来.此外,对任意正整数n(0≤n≤m),系统(13)恰好有n个局部临界周期从原点分支出来.
系统(13)至多有m个局部临界周期从原点分支出来.此外,对任意正整数n(0≤n≤m),系统(13)恰好有n个局部临界周期从原点分支出来.
证明 我们只证明m=2的情形,其余情形证明方法类似.当f02=-f12/2时,由式(8)可得
P2=(12d-f12)π,P4=(192d2-f14)π/2, P6=(69 312d4+1 ![]()
我们只需证明P2,P4在![]() 关于P6是无关的.取
关于P6是无关的.取
λ*=(d, f01, f02, f12, f03, f13, f04, f14, f05)=
对λ*的任一邻域U,存在λ1=(d, f01,-6d,12d,0,0, f04,192d2+ε1,0)∈U⊂V(P2),这里ε1>0充分小,使得![]() 再取
再取
λ2=(d, f01,-6d,12d,0,0, f04,192d2-ε2,0)∈V(P2), P4(λ2)≠0,
其中ε2>0,对λ2的任一邻域U′,存在λ3=(d, f01,-6d-δ,12d+2δ,0,0, f04,192d2-ε2,0)∈U′,这里δ>0充分小,使得P2(λ3)P4(λ2)=-π2δε2<0.所以满足定义2的条件,故P2,P4在![]() 关于P6是无关的.由引理1可知,恰好有2个局部临界周期从系统(13)的原点分支出来.当f02≠-f12/2, f14=0时,计算得
关于P6是无关的.由引理1可知,恰好有2个局部临界周期从系统(13)的原点分支出来.当f02≠-f12/2, f14=0时,计算得
(19)
这里
进一步计算得
G3=Res(H1,H5, f12)=
易知G3=0没有实数解,故式(19)不等于零.由引理2可知,通过对λ*的小扰动,使得恰好有2个局部临界周期从系统(13)的原点分支出来.当(2f02+f12)f14≠0时,不失一般性,取f14=1,则
(20)
这里
进一步得![]() 我们发现G4=0没有实数解,所以式(20)不等于零.由引理2可知,通过对λ*的小扰动,使得恰好有2个局部临界周期从系统(13)的原点分支出来.
我们发现G4=0没有实数解,所以式(20)不等于零.由引理2可知,通过对λ*的小扰动,使得恰好有2个局部临界周期从系统(13)的原点分支出来.
定理7 在方程(4)的稳态解u(x,t)≡1/2邻域,若![]() 则没有临界周期波长,即连续周期波列的波长函数是单调的;若
则没有临界周期波长,即连续周期波列的波长函数是单调的;若![]() 则至多有m个临界周期波长.此外,对任意正整数n(0≤n≤m),恰好有n个临界周期波长.
则至多有m个临界周期波长.此外,对任意正整数n(0≤n≤m),恰好有n个临界周期波长.
情形K2 2f03+f13=0, f05=0, 2f04+f14=0, 2f02+f12=0.
我们将定理1的条件K2代入文献[17]中定理3.1的递推公式计算,得到τ1=f12-12d.令f12=12d,得τ1=0且τ2=(f14-192d2)/2.取f14=192d2,得τ2=0且τ3=-3(80d3/2-f13)(80d3/2+f13)/20.若f13=80d3/2,则τ3=0且τ4=-18 432d4;若f13=-80d3/2,则τ3=0且τ4=11 008d4;由于d>0,所以τ4都不为零.因此,系统(13)的原点是至多3阶的细中心.
定理8 若λ*∈K2,则系统(13)的原点是一个阶数最大为3的细中心.此外,系统(13)原点是m(m=0,1,2,3)阶细中心,当且仅当![]() 其中
其中
![]() R9: 2f03+f13=0, f05=0, 2f04+f14=0, f12=-2f02≠12d},
R9: 2f03+f13=0, f05=0, 2f04+f14=0, f12=-2f02≠12d},
![]() R9: 2f03+f13=0, f05=0, f14=-2f04≠192d2, f12=-2f02=12d},
R9: 2f03+f13=0, f05=0, f14=-2f04≠192d2, f12=-2f02=12d},
![]() R9: f13=-2f03,
R9: f13=-2f03, ![]() 400d3, f05=0, f14=-2f04=192d2, f12=-2f02=12d},
400d3, f05=0, f14=-2f04=192d2, f12=-2f02=12d},
![]() R9: f13=-2f03,
R9: f13=-2f03, ![]() 400d3, f05=0, f14=-2f04=192d2, f12=-2f02=12d}.
400d3, f05=0, f14=-2f04=192d2, f12=-2f02=12d}.
由定理8,我们有以下结果.
定理9 对于参数λ*,若![]() 则没有局部临界周期从系统(13)的原点分支出来;若
则没有局部临界周期从系统(13)的原点分支出来;若![]() 则至多有m个局部临界周期从系统(13)的原点分支出来;此外,对任意正整数n(0≤n≤m),恰好有n个局部临界周期从系统(13)的原点分支出来.
则至多有m个局部临界周期从系统(13)的原点分支出来;此外,对任意正整数n(0≤n≤m),恰好有n个局部临界周期从系统(13)的原点分支出来.
证明 我们只证明m=3的情形,其余情形证明方法类似.令
λ*=(d, f01, f02, f12, f03, f13, f04, f14, f05)=
对任意d>0,我们得到
由引理2可知,通过对λ*的小扰动,使得恰好有3个局部临界周期从系统(13)原点分支出来.
定理10 在方程(4)的稳态解u(x,t)≡1/2邻域,若![]() 则没有临界周期波长,即连续周期波列的波长函数是单调的;若
则没有临界周期波长,即连续周期波列的波长函数是单调的;若![]() 则至多有m个临界周期波长.此外,对任意正整数n(0≤n≤m),恰好有n个临界周期波长.
则至多有m个临界周期波长.此外,对任意正整数n(0≤n≤m),恰好有n个临界周期波长.
4 结论和展望
本文对一类含有五次非线性反应项和常数扩散项的反应扩散方程(4)的SAIPW和局部临界周期波长分支问题进行了研究.通过研究其行波系统(2)原点的中心条件和小振幅极限环个数,得到了反应扩散方程(4)具有连续的周期波列的条件,以及得到了该方程存在8个SAIPW.此外,本文还进一步得到了在周期波列条件下,反应扩散方程(4)最多具有3个临界周期波长,即连续周期波列的波长函数的单调性最多发生3次变化.对于反应扩散方程(1)是否存在等周期的周期波列,这是我们将需要考虑的一个问题; 另外, 对于一般的含有五次非线性反应项和常数扩散项的反应扩散方程, 其最多有多少个SAIPW, 也是值得进一步研究的.
[1] ARANSON I, KRAMER L. The world of the complex Ginzburg-Landau equation[J]. Review of Modern Physics, 2001, 74(1): 99-143.
[2] CHEN A Y, GUO L N, DENG X J. Existence of solitary waves and periodic waves for a perturbed generalized BBM equation[J]. Journal of Differential Equations, 2016, 261(10): 5324-5349.
[3] ZHUANG K G, DU Z J, LIN X J. Solitary waves solutions of singularly perturbed higher-order KdV equation via geometric singular perturbation method[J]. Nonlinear Dynamics, 2015, 80(1/2): 629-635.
[4] MANSOUR M B A. Traveling wave solutions of a reaction-diffusion model for bacterial growth[J]. Physica A: Statistical Mechanics and Its Applications, 2007, 383(2): 466-472.
[5] SHERRATT J A, SMITH M J. Periodic travelling waves in cyclic populations: field studies and reaction-diffusion models[J]. Journal of the Royal Society Interface, 2008, 5(22): 483-505.
[6] LI J B, WU J H, ZHU H P. Traveling waves for an integrable higher order KdV type wave equations[J]. International Journal of Bifurcation and Chaos, 2006, 16(8): 2235-2260.
[7] ![]() V. Periodic travelling waves in nonlinear reaction-diffusion equations via multiple Hopf bifurcation[J]. Chaos, Solitons and Fractals, 2003, 18(2): 241-257.
V. Periodic travelling waves in nonlinear reaction-diffusion equations via multiple Hopf bifurcation[J]. Chaos, Solitons and Fractals, 2003, 18(2): 241-257.
[8] HUANG W T, CHEN T, LI J B. Isolated periodic wave trains and local critical wave lengths for a nonlinear reaction-diffusion equation[J]. Communications in Nonlinear Science and Numerical Simulation, 2019, 74(5): 84-96.
[9] SANCHEAGARDUNO F, MAINI P K. Traveling wave phenomena in some degenerate reaction-diffusion equations[J]. Journal of Differential Equations, 1995, 117(2): 281-319.
[10] YANG G X. Hopf bifurcation of traveling wave solutions of delayed Fisher-KPP equation[J]. Applied Mathematics and Computation, 2013, 220(4): 213-220.
[11] CHICONE C, JACOBS M. Bifurcation of critical periods for plane vector fields[J]. Transactions of the American Mathematical Society, 1989, 312(2): 433-486.
[12] ROMANOVSKI V G, HAN M A. Critical period bifurcations of a cubic system[J]. Journal of Physics A: Mathematical and General, 2003, 36(18): 5011-5022.
[13] ROUSSEAU C, TONI B. Local bifurcations of critical periods in the reduced Kukles system[J]. Canadian Journal of Mathematics, 1997, 49(2): 338-358.
[14] YU P, HAN M A. Critical periods of planar revertible vector field with third-degree polynomial functions[J]. International Journal of Bifurcation and Chaos, 2009, 19(1): 419-433.
[15] LIU Y R, LI J B. Theory of values of singular point in complex autonomous differential systems[J]. Science in China (Series A), 1990, 33: 10-24.
[16] 黄文韬. 微分自治系统的几类极限环分支与等时中心问题[D]. 博士学位论文. 长沙: 中南大学, 2004. (HUANG Wentao. Several classes of bifurcations of limit cycles and isochronous centers for differential autonomous systems[D]. PhD Thesis. Changsha: Central South University, 2004. (in Chinese))
[17] LIU Y R, HUANG W T. A new method to determine isochronous center conditions for polynomial differential systems[J]. Bulletin des Sciences Mathématiques, 2003, 127(2): 133-148.
[18] YU P, HAN M A. Twelve limit cycles in a cubic case of the 16th Hilbert problem[J]. International Journal of Bifurcation and Chaos, 2005, 15(7): 2191-2205.
[19] CHEN H B, LIU Y R. Linear recursion formulas of quantities of singular point and applications[J]. Applied Mathematics and Computation, 2004, 148(1): 163-171.
[20] GEYER A, VILLADELPRAT J. On the wave length of smooth periodic traveling waves of the Camassa-Holm equation[J]. Journal of Differential Equations, 2015, 259(6): 2317-2332.