Research on Shear Lag Warping Displacement Modes of Frame-Tube Structures Based on the Hamiltonian Mechanics
-
摘要:
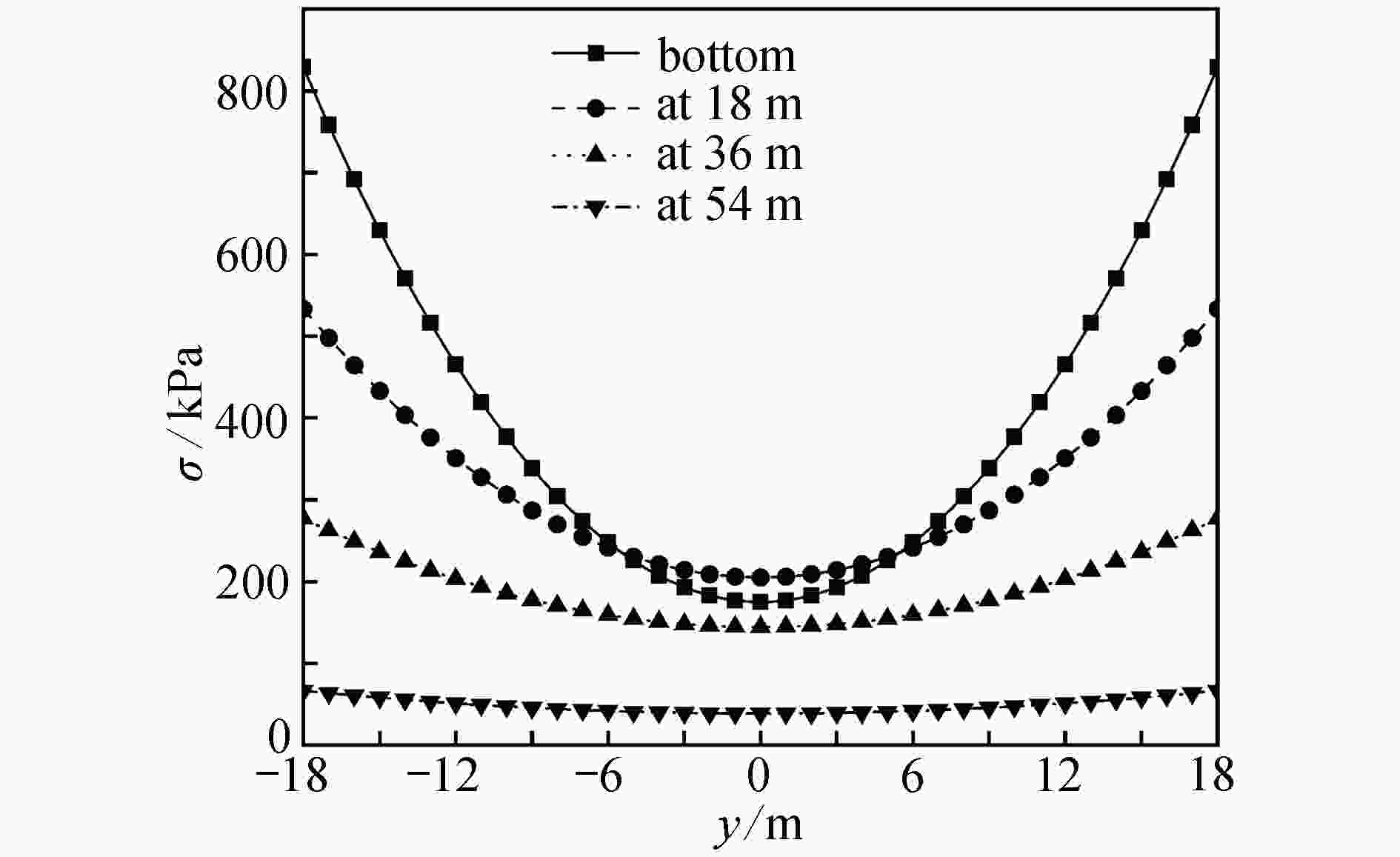
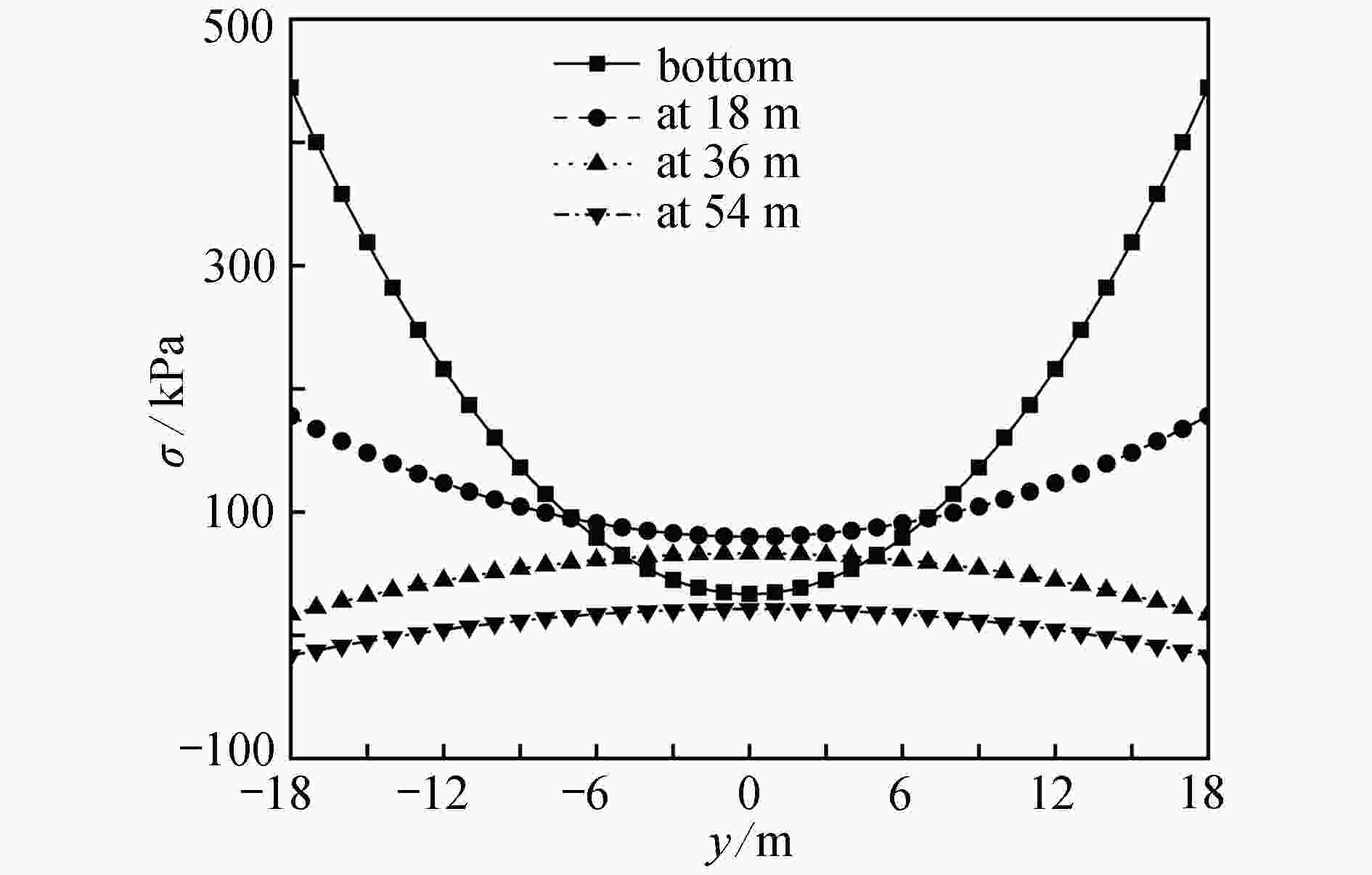
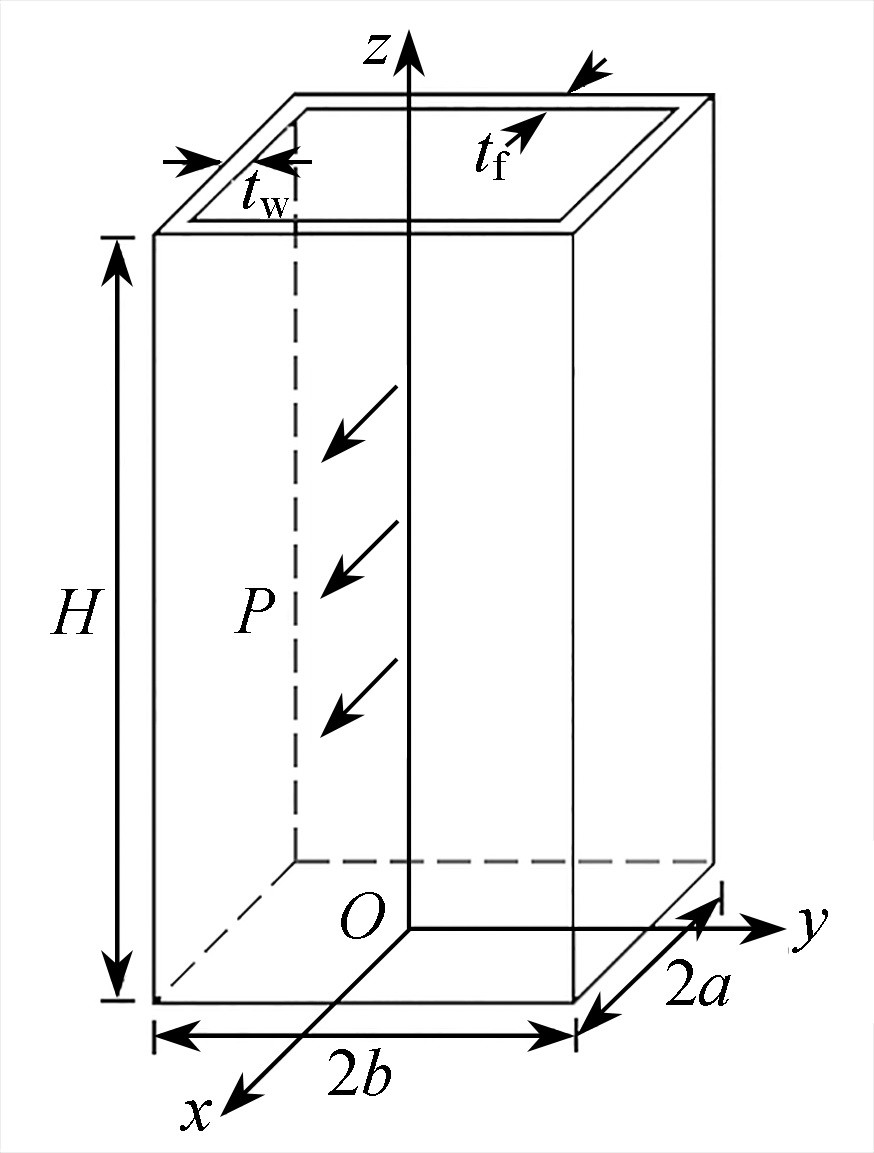
以等效连续化方法为基础，在Hamilton力学体系下进行框筒结构剪滞翘曲位移函数精度研究。选用不同类型的函数描述翼缘板的剪滞翘曲位移，考虑等效板的剪切变形以及纵向翘曲，得到不同位移函数下结构的总势能及对应的Lagrange函数。区别于传统变分法，该文在Hamilton力学体系下进行问题研究，导出框筒结构弯曲问题的Hamilton正则方程并利用精细积分法求解，进而计算出柱轴力并进行精度分析。算例验证结果表明：使用该方法分析框筒结构的剪力滞后效应是简单可行的；不同翘曲位移函数的选择对侧移计算结果影响不大，对轴力求解结果影响较大，二次抛物线最能反映等效翼缘板的实际翘曲位移；对比不同形式荷载作用下等效翼缘板中应力分布可知，随着外荷载合力作用点位置的升高，结构顶部负剪力滞后效应逐渐减弱至消失。
-
关键词:
- 框筒结构 /
- 剪力滞后效应 /
- 翘曲位移函数 /
- Hamilton对偶求解体系 /
- 精细积分法
Abstract:Based on the equivalent continuity method, the accuracy of the shear lag warping displacement functions for frame-tube structures was studied under the Hamiltonian mechanics. Different types of functions were selected to describe the shear lag warping displacement of the flange plate, and the shear deformation and longitudinal warping of the equivalent plate were considered. The total potential energy of the structure and the corresponding Lagrangian function under different displacement modes were obtained. Not with the traditional variational methods, the problem was studied under the Hamiltonian mechanics system. The Hamiltonian canonical equation for the frame-tube structure was derived and solved with the precise integration method, then the column axial force was calculated and the accuracy was analyzed. The verification results of the calculation examples show that, this method is simple and feasible to analyze the shear lag effects of the frame-tube structures. The choice of different warping displacement functions has little effect on the lateral displacement calculation results, but has great influence on the axial force solution, and the quadratic parabola can best reflect the actual warping displacement distribution of the flange. Comparison of the stress distributions in the equivalent flange under different types of loads indicate that, with the increase of the position of the external load resultant force, the negative shear-lag effect on the top gradually weakens to disappear.
-
图 4 不同翘曲函数下结构侧移曲线
Figure 4. Curves of structural lateral displacements with different warping functions
图 5 工况①下不同高度处翼缘应力分布
Figure 5. Flange stress distributions at different heights under working condition ①
图 6 工况②下不同高度处翼缘应力分布
Figure 6. Flange stress distributions at different heights under working condition ②
图 7 工况③下不同高度处翼缘应力分布
Figure 7. Flange stress distributions at different heights under working condition ③
表 1 工况①下结构底层柱轴力计算值及相对误差
Table 1. The axial force values and relative errors of the bottom floor column under working condition ①
column number ref. [1] N/kN function type N/kN relative error δ1/% quadratic function cosine function catenary function exponential function quadratic function cosine function catenary function exponential function 1 0 0 0 0 0 0 0 0 0 2 48.90 51.32 50.08 52.01 47.97 4.95 2.42 6.36 −1.90 3 105.80 108.53 106.07 109.85 102.20 2.58 0.26 3.83 −3.40 4 178.80 177.51 173.87 179.36 168.94 −0.72 −2.76 0.31 −5.52 5 275.90 264.15 259.38 266.35 254.44 −4.26 −6.00 −3.46 −7.78 6 698.00 644.80 636.71 647.67 629.60 −7.62 −8.78 −7.21 −9.80 7 304.50 283.86 291.09 278.81 288.19 −6.78 −4.41 −8.44 −5.36 8 223.00 210.29 220.09 204.51 223.82 −5.70 −1.30 −8.30 0.37 9 159.60 153.06 159.13 150.16 169.32 −4.10 −0.29 −5.92 6.09 10 114.40 112.19 112.36 113.11 123.20 −1.94 −1.79 −1.13 7.69 11 87.20 87.66 82.95 91.57 84.15 0.53 −4.87 5.01 −3.50 12 78.10 79.49 72.92 84.50 58.69 1.77 −6.63 8.20 −24.85 
下载: 导出CSV
表 2 工况①下结构最大侧移值及相对误差
Table 2. Maximum side shift values and relative errors of the structure under working condition ①
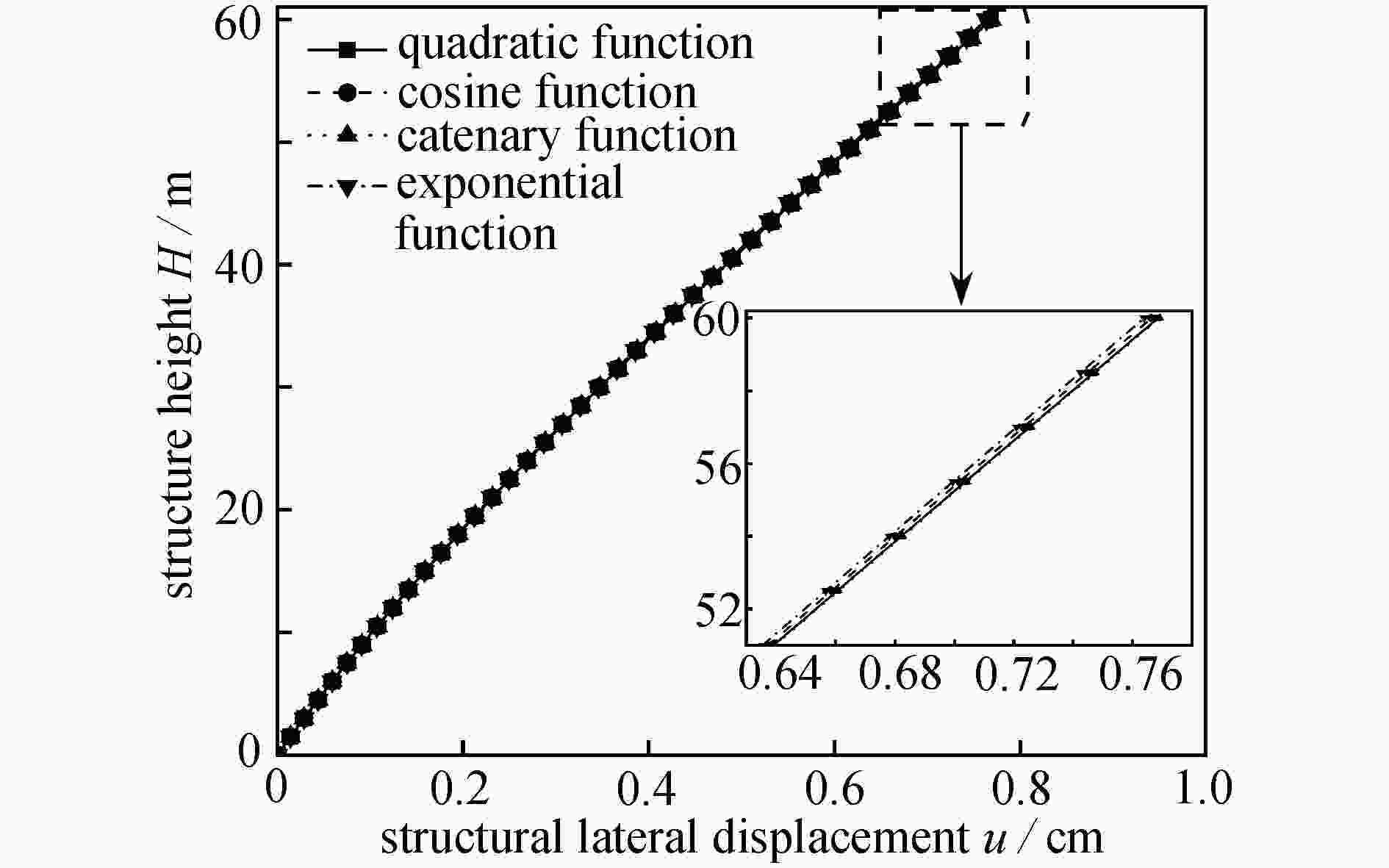
ref. [1] u/cm function type u/cm relative error δ2/% quadratic function cosine function catenary function exponential function quadratic function cosine function catenary function exponential function 0.75 0.7685 0.7663 0.7691 0.7638 2.47 2.17 2.55 1.84
下载: 导出CSV
-
[1] 包世华, 张铜生. 高层建筑结构设计和计算[M]. 北京: 高等教育出版社, 2013.BAO Shihua, ZHANG Tongsheng. Design and Analysis of Tall-Building Structure[M]. Beijing: Higher Education Press, 2013. (in Chinese) [2] 曾新, 马乐, 谢华. 框筒结构剪力滞后效应分析[J]. 广西大学学报(自然科学版), 2007, 32(S2): 453-456. (ZENG Xin, MA Le, XIE Hua. Analysis of shear-lag effect in framed tube structure[J]. Journal of Guangxi University (Natural Science) , 2007, 32(S2): 453-456.(in Chinese) [3] 刘中辉, 王全凤. 框筒结构长宽比对剪力滞后的影响及其分析[J]. 华侨大学学报(自然科学版), 2005, 26(3): 331-332. (LIU Zhonghui, WANG Quanfeng. Influence of length-width ratio of framed tube structure on shear lag and its analysis[J]. Journal of Huaqiao University (Natural Science) , 2005, 26(3): 331-332.(in Chinese) [4] 龚胡广, 方辉, 沈蒲生. 框筒结构的简化分析方法[J]. 建筑结构, 2006, 36(7): 79-82. (GONG Huguang, FANG Hui, SHEN Pusheng. Simplified method for calculating frame-tube structure[J]. Building Structure, 2006, 36(7): 79-82.(in Chinese) [5] 李耀庄, 翟治鹏, 项正良. 基于翘曲位移函数的框筒结构剪力滞后效应研究[J]. 铁道科学与工程学报, 2017, 14(7): 1505-1511. (LI Yaozhuang, ZHAI Zhipeng, XIANG Zhengliang. Research on shear lag effect of frame tube structure based on warping displacement function[J]. Journal of Railway Science and Engineering, 2017, 14(7): 1505-1511.(in Chinese) doi: 10.3969/j.issn.1672-7029.2017.07.022 [6] 张玉芳. 高层建筑框筒结构简化分析方法研究[D]. 硕士学位论文. 长沙: 湖南大学, 2005.ZHANG Yufang. Study on simplified methods to analyze framed-tube structures of high-rise buildings[D]. Master Thesis. Changsha: Hunan University, 2005. (in Chinese) [7] 金仁和, 魏德敏. 框筒结构剪力滞后研究现状与思考[J]. 建筑钢结构进展, 2008, 10(2): 23-27. (JIN Renhe, WEI Demin. Current investigation and expectation on the shear lag of framed-tube structures[J]. Progress in Steel Building Structures, 2008, 10(2): 23-27.(in Chinese) [8] 张玉平, 胡火全, 李传习, 等. 薄壁箱梁剪力滞翘曲位移函数的改进与对比分析[J]. 应用力学学报, 2016, 33(6): 1099-1105. (ZHANG Yuping, HU Huoquan, LI Chuanxi, et al. An improvement and comparative analysis of shear lag warping displacement function in thin-walled box girder[J]. Chinese Journal of Applied Mechanics, 2016, 33(6): 1099-1105.(in Chinese) [9] 赵庆友, 张元海, 邵江艳. 翼板变厚度箱形梁的剪力滞效应分析[J]. 应用数学和力学, 2019, 40(6): 609-619. (ZHAO Qingyou, ZHANG Yuanhai, SHAO Jiangyan. Analysis of shear lag effects in box girders with variable-thickness flanges[J]. Applied Mathematics and Mechanics, 2019, 40(6): 609-619.(in Chinese) [10] 蔡恒, 卢海林, 汤正. 考虑剪力滞效应的曲线箱梁自振特性研究[J]. 世界地震工程, 2016, 32(4): 239-244. (CAI Heng, LU Hailin, TANG Zheng. Vibration properties research on curved box girder considering shear lag effects[J]. World Earthquake Engineering, 2016, 32(4): 239-244.(in Chinese) [11] 甘亚南, 周广春. 薄壁箱梁纵向剪滞翘曲函数精度选择的研究[J]. 工程力学, 2008, 25(6): 100-106. (GAN Yanan, ZHOU Guangchun. An approach for precision selection of longitudinal shear lag warping displacement function of thin-walled box girders[J]. Engineering Mechanics, 2008, 25(6): 100-106.(in Chinese) [12] 胡启平, 卢明. 筒中筒结构协同分析新方法[J]. 工程力学, 2007, 24(S1): 150-153. (HU Qiping, LU Ming. New method for coordination analysis of tube-in-tube structures[J]. Engineering Mechanics, 2007, 24(S1): 150-153.(in Chinese) [13] 钟万勰. 应用力学对偶体系[M]. 北京: 科学出版社, 2002.ZHONG Wanxie. Dual System of Applied Mechanics[M]. Beijing: Science Press, 2002. (in Chinese) [14] 钟万勰. 应用力学的辛数学方法[M]. 北京: 高等教育出版社, 2006.ZHONG Wanxie. Symplectic Solution Methodology in Applied Mechanics[M]. Beijing: Higher Education Press, 2006. (in Chinese) [15] 胡启平, 王丽娟. 基础隔震框架结构动力时程分析的精细积分法[J]. 广西大学学报(自然科学版), 2016, 41(4): 939-944. (HU Qiping, WANG Lijuan. Precise integration method for dynamic time history analysis of base-isolation frame structures[J]. Journal of Guangxi University (Natural Science) , 2016, 41(4): 939-944.(in Chinese) [16] 汪梦甫, 周锡元. 结构动力方程的高斯精细时程积分法[J]. 工程力学, 2004, 21(4): 13-16. (WANG Mengfu, ZHOU Xiyuan. Gauss precise time-integration of structural dynamic analysis[J]. Engineering Mechanics, 2004, 21(4): 13-16.(in Chinese) doi: 10.3969/j.issn.1000-4750.2004.04.003 -
计量
- 文章访问数: 600
- HTML全文浏览量: 226
- PDF下载量: 47
- 被引次数: 0
渝公网安备50010802005915号