基于Kriging模型和提升小波变换的随机模型修正

吴雨程; 殷红; 彭珍瑞

doi:10.21656/1000-0887.420128

基于Kriging模型和提升小波变换的随机模型修正

doi: 10.21656/1000-0887.420128

兰州交通大学机电工程学院，兰州 730070

基金项目: 国家自然科学基金 (51768035)

详细信息

作者简介:
吴雨程（1997—），男，硕士生（E-mail：821085844@qq.com）

殷红（1978—），女，教授，博士，硕士生导师（E-mail：yinhong@mail.lzjtu.cn）

彭珍瑞（1972—），男，教授，博士，博士生导师（通讯作者. E-mail：pzrui@163.com）

中图分类号: O327
计量
- 文章访问数: 695
- HTML全文浏览量: 297
- PDF下载量: 37
- 被引次数: 0
出版历程
- 收稿日期: 2021-05-10
- 修回日期: 2021-06-17
- 刊出日期: 2022-07-15

Stochastic Model Updating Based on Kriging Model and Lifting Wavelet Transform

School of Mechanical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, P.R.China

摘要

摘要:
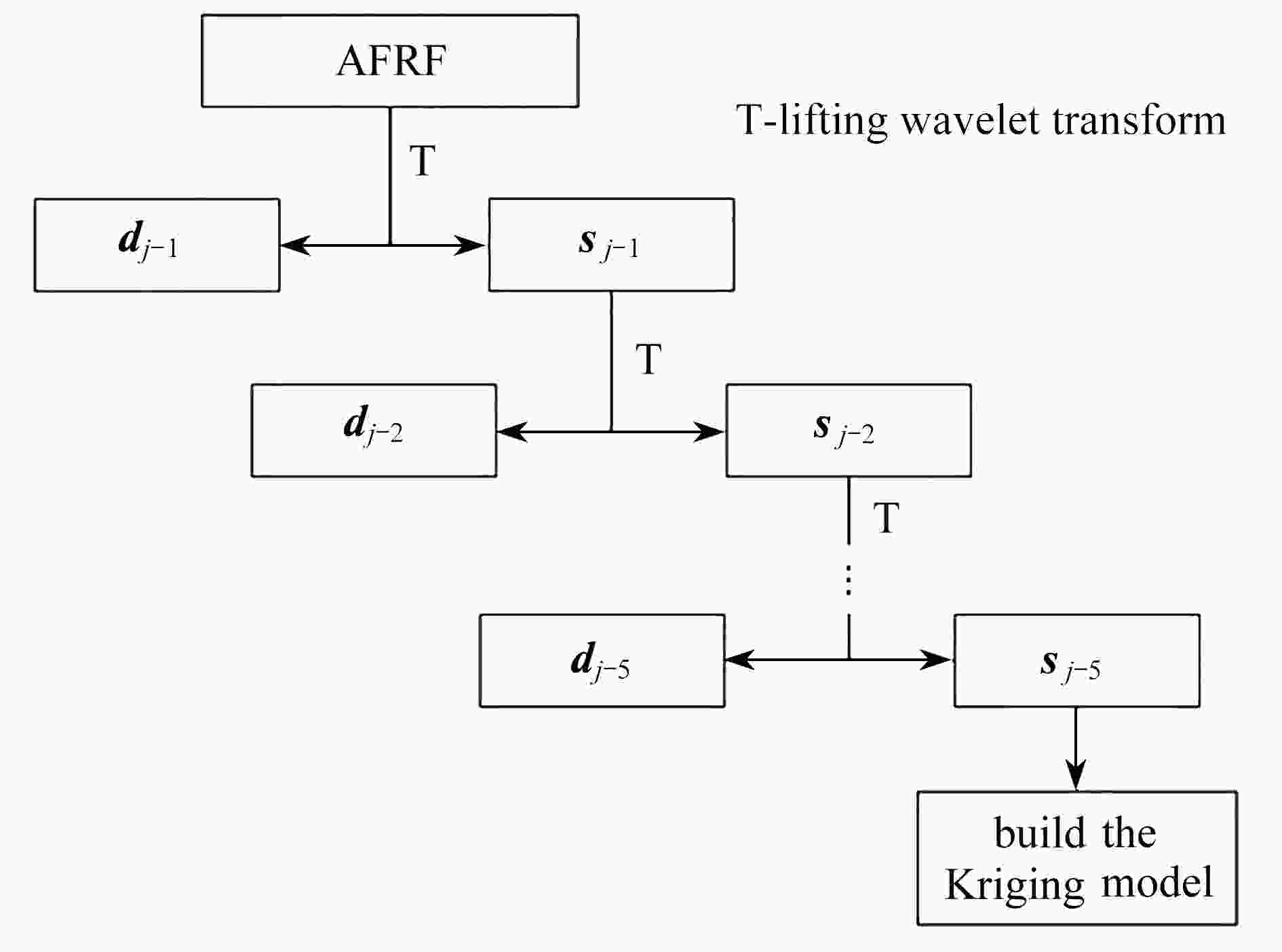
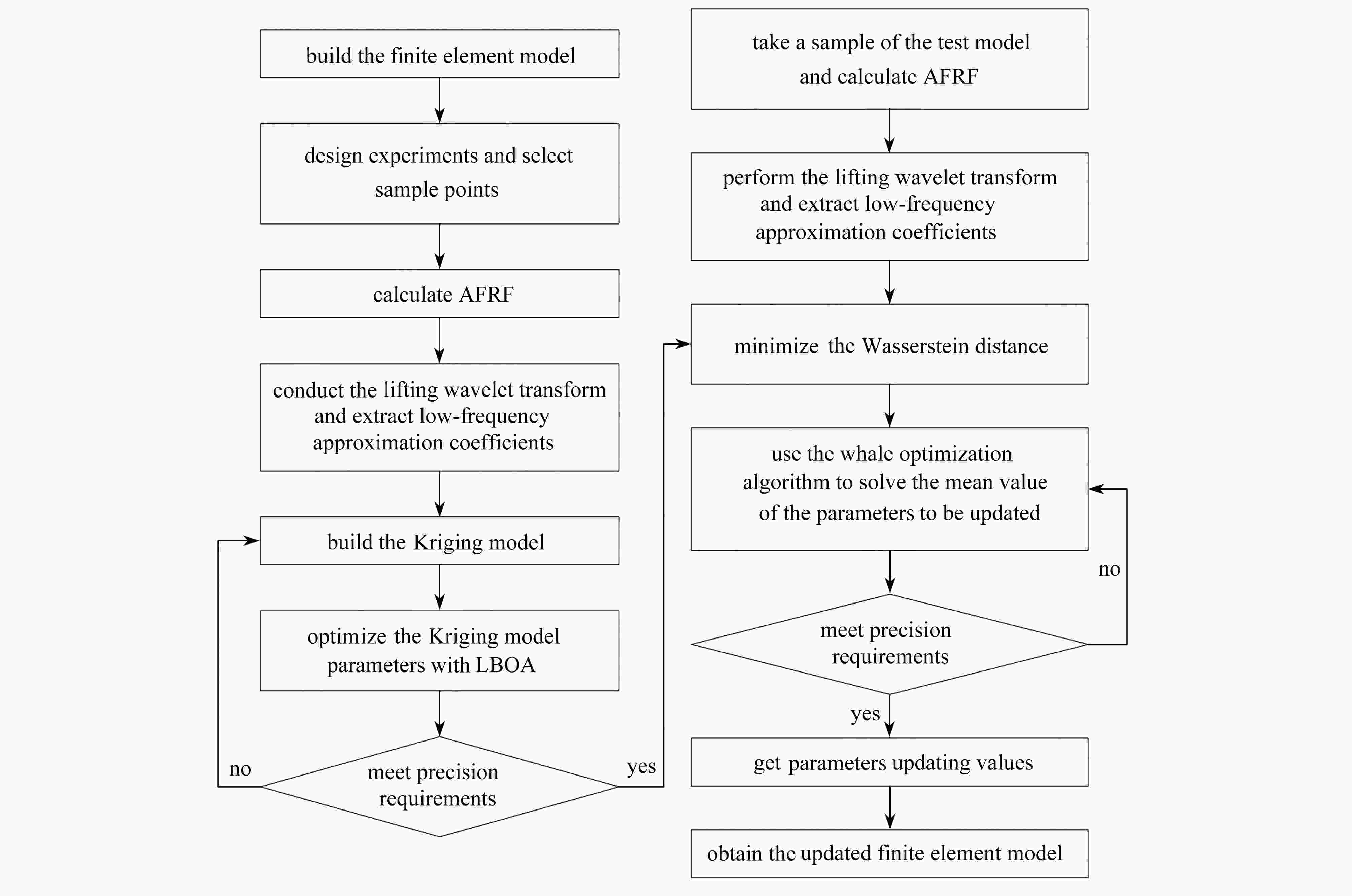
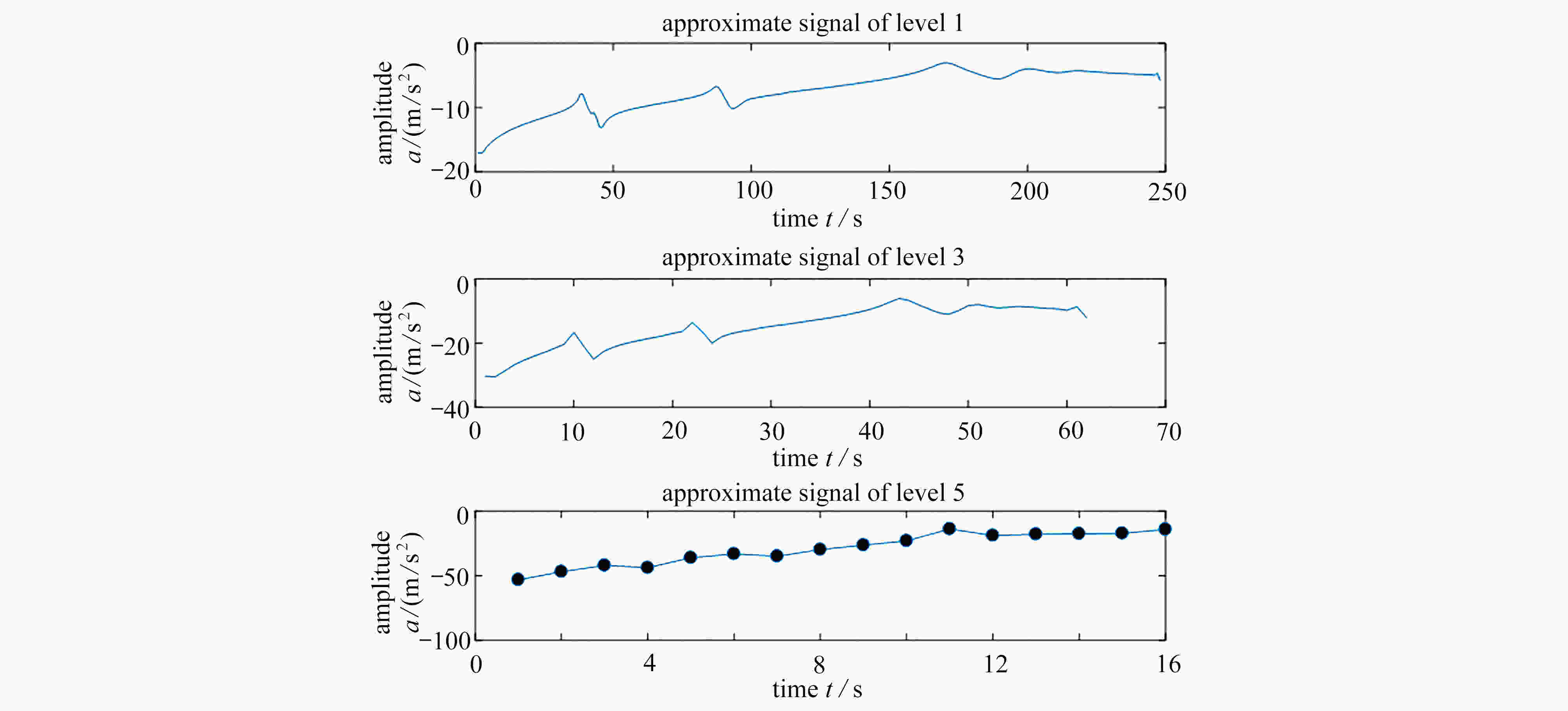
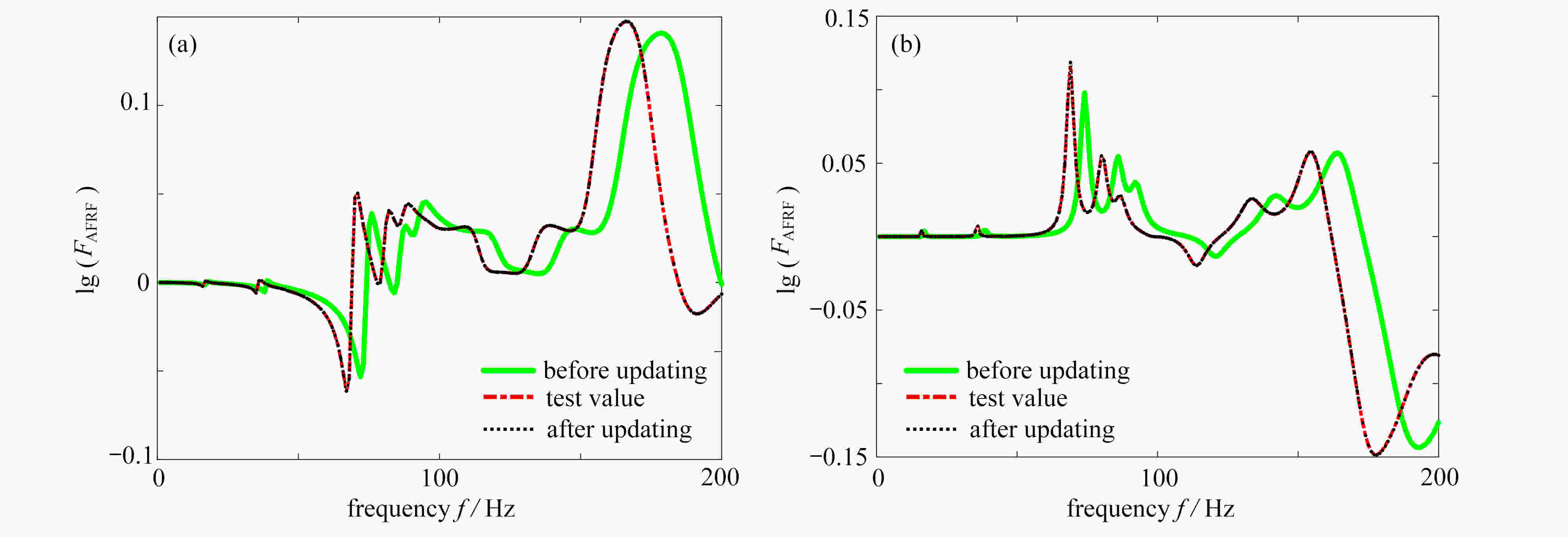
为提高随机模型修正效率，减小计算量，提出了一种基于Kriging模型和提升小波变换的随机模型修正方法。首先，对加速度频响函数进行提升小波变换，提取第5层近似系数代替原频响函数。其次，采用拉丁超立方抽样抽取待修正样本，将其作为Kriging模型的输入，对应的近似系数作为输出，构建Kriging模型。提出了一种引入莱维飞行(Lévy flight)的蝴蝶优化算法(LBOA)，并将其应用于Kriging模型相关参数的寻优中，提高Kriging模型的精度。最后，以最小化Wasserstein距离为目标，通过鲸鱼优化算法求解待修正参数的均值。测试函数结果表明，LBOA在寻优能力、收敛精度和稳定性等方面有了很大的提升。数值算例的修正误差均低于0.4%，验证了所提模型修正方法具有较高的修正精度和效率。
- 模型修正 /
- Kriging模型 /
- 提升小波变换 /
- Wasserstein距离 /
- 蝴蝶优化算法
Abstract:
In order to improve the efficiency of stochastic model updating and reduce the amount of calculation, a stochastic model updating method based on Kriging model and lifting wavelet transform was proposed. Firstly, the lifting wavelet transform was performed on the acceleration frequency response function, and the 5th-level approximate coefficients were extracted to replace the original frequency response function; secondly, the Latin hypercube sampling was applied to sample the parameters to be updated and the corresponding approximate coefficients as the outputs to build the Kriging model. A butterfly optimization algorithm with Lévy flight (LBOA) was proposed and used to improve the accuracy of Kriging model; finally, with the goal of minimizing the Wasserstein distance, the mean values of the parameters to be updated were solved with the whale optimization algorithm. The results of the test function show that, the LBOA greatly improves in terms of optimization, convergence accuracy and stability. The updating errors of the numerical examples are all less than 0.4%, and indicate the high accuracy and efficiency of the proposed model updating method.
- model updating /
- Kriging model /
- lifting wavelet transform /
- Wasserstein distance /
- butterfly optimization algorithm

HTML全文

图 1 f₆收敛曲线

Figure 1. Convergence curves of $ {f_6} $

下载: 全尺寸图片幻灯片

图 2 提升小波变换过程

Figure 2. The process of the lifting wavelet transform

下载: 全尺寸图片幻灯片

图 3 近似系数提取流程

Figure 3. The flow chart of extracting approximate coefficients

下载: 全尺寸图片幻灯片

图 4 模型修正流程图

Figure 4. The flowchart of model updating

下载: 全尺寸图片幻灯片

图 5 二维桁架结构

Figure 5. The 2D truss structure

下载: 全尺寸图片幻灯片

图 6 参数对结构AFRF的灵敏度

Figure 6. Sensitivity of structure AFRF to parameters

下载: 全尺寸图片幻灯片

图 7 Kriging模型精度评估

Figure 7. Accuracy evaluation of the Kriging model

下载: 全尺寸图片幻灯片

图 8 修正前后加速度频响函数曲线

Figure 8. AFRF curves before and after updating

下载: 全尺寸图片幻灯片

图 9 三维桁架结构

Figure 9. The 3D truss structure

下载: 全尺寸图片幻灯片

图 10 第1、3、5层近似系数

Figure 10. Approximate coefficients for the 1st, 3rd and 5th levels

下载: 全尺寸图片幻灯片

图 11 Kriging模型参数寻优曲线

Figure 11. Optimization curves of the Kriging model parameter

下载: 全尺寸图片幻灯片

图 12 Kriging模型精度评估

Figure 12. Accuracy evaluation of the Kriging model

下载: 全尺寸图片幻灯片

图 13 修正前后加速度频响函数曲线：(a)实部曲线；(b)虚部曲线

Figure 13. AFRF curves before and after updating: (a) real part curves; (b) imaginary part curves

下载: 全尺寸图片幻灯片

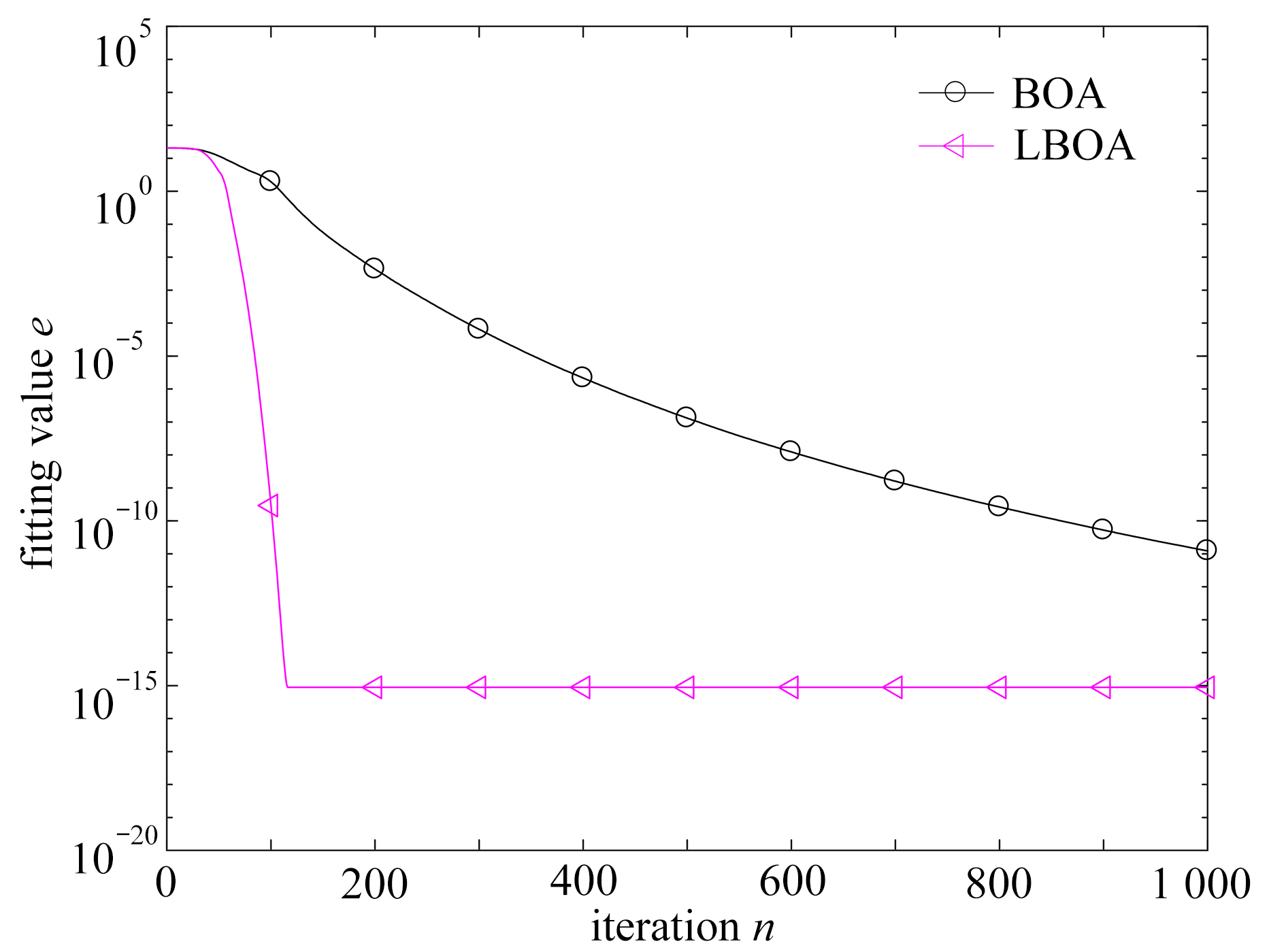
表 1 BOA改进算法寻优结果

Table 1. Optimization results of the improved BOA algorithm

function	BOA			LBOA
function	mean value	standard deviation	successful rate $\delta$/%	mean value	standard deviation	successful rate $\delta$/%
$ {f_1} $	1.80E−14	1.25E−15	100	0	0	100
$ {f_2} $	9.43E−12	3.40E−12	100	0	0	100
$ {f_3} $	7.67E−4	3.48E−4	0	4.37E−5	4.93E−5	86
$ {f_4} $	1.81E−15	2.24E−15	100	0	0	100
$ {f_5} $	1.90E+1	5.81E+1	80	0	0	100
$ {f_6} $	1.19E−11	1.95E−12	100	8.88E−16	0	100

下载: 导出CSV

表 2 寻优结果对比

Table 2. Comparison of optimization results

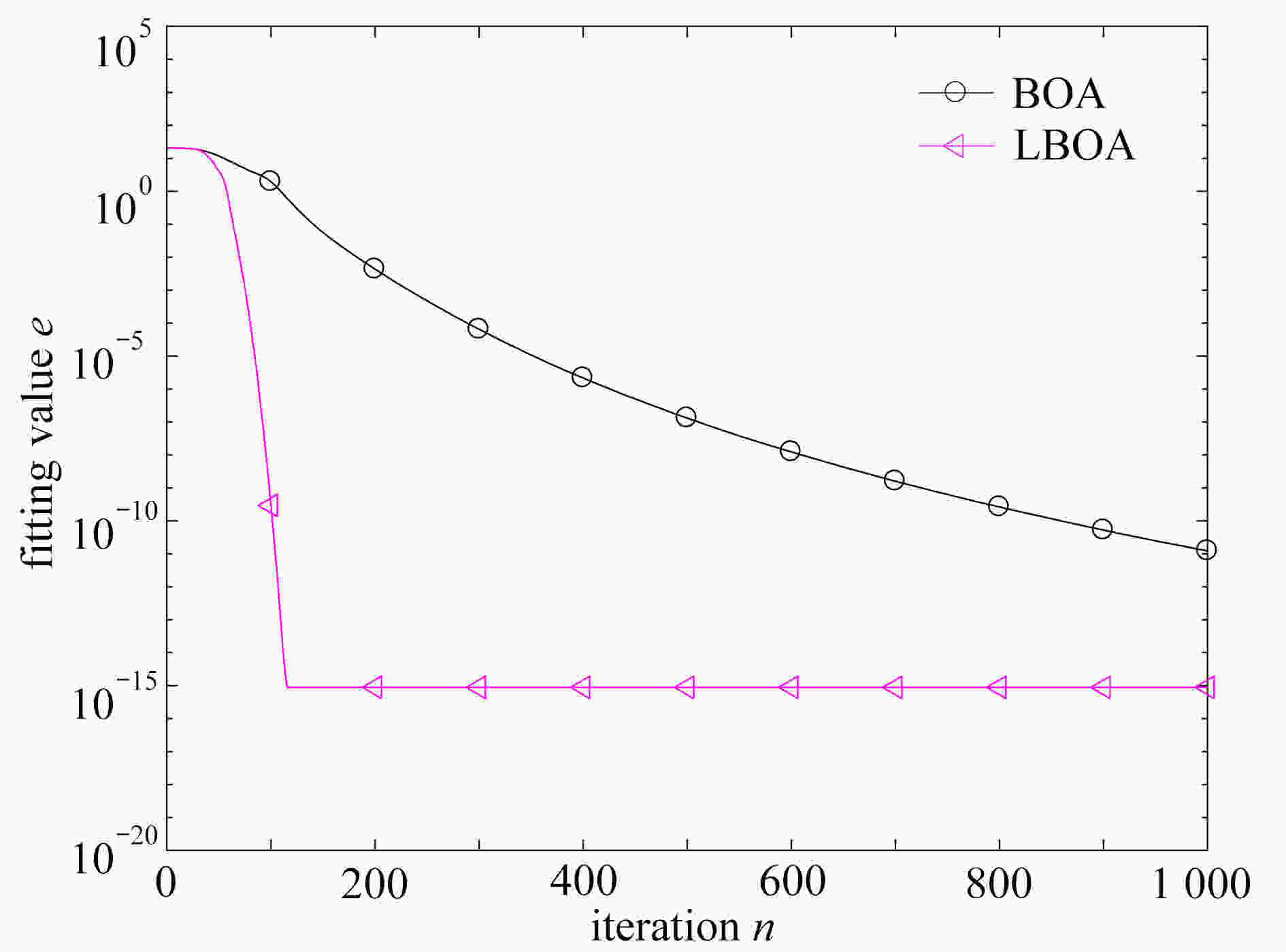
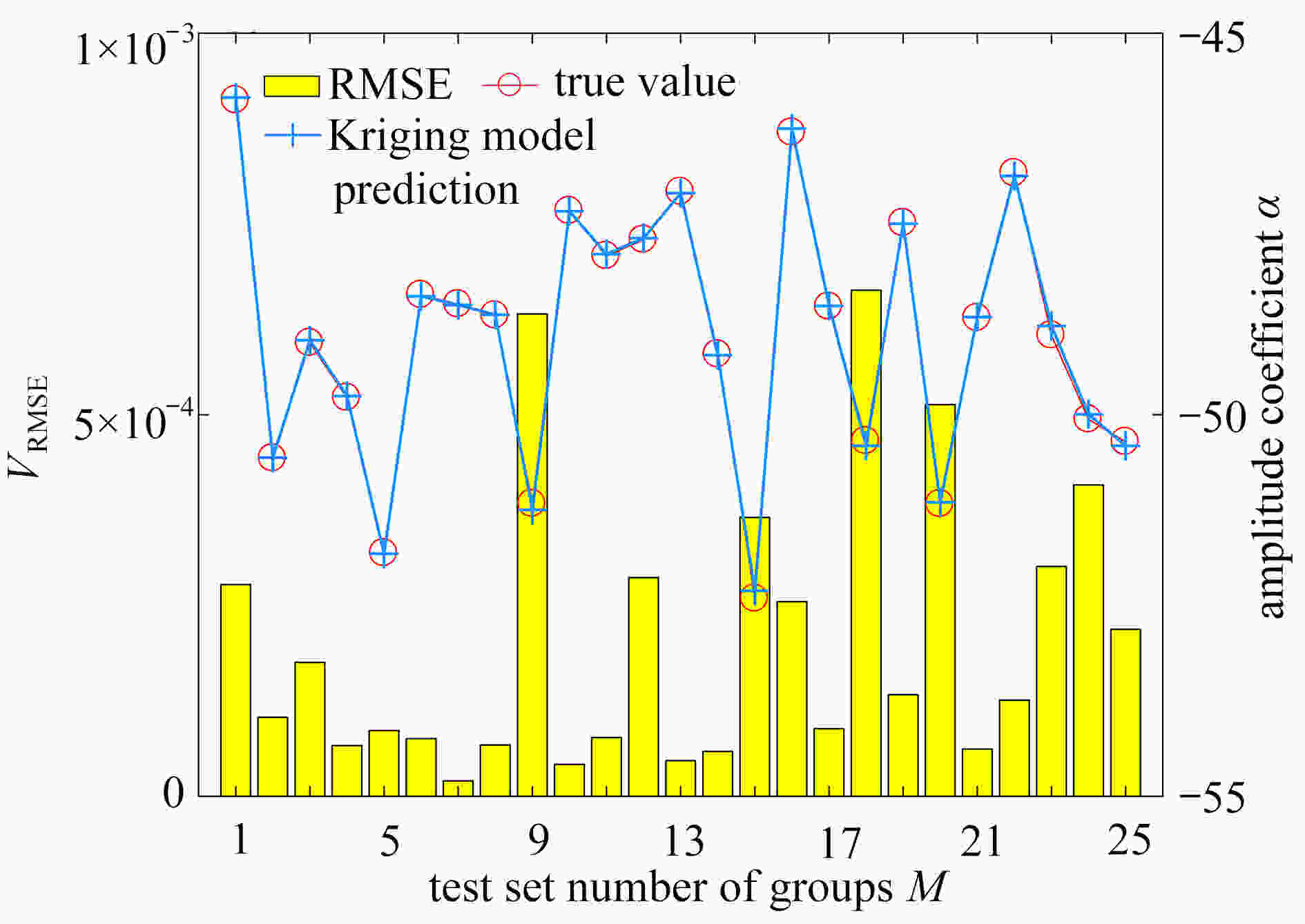
	LBOA	BOA
${\theta _k}$	4.064 5 × 10⁻³	3.320 5
fitting value e	7.396 2 × 10⁻¹⁴	6.941 9 × 10⁻⁸
running time t/s	27.2	27.7

下载: 导出CSV

表 3 桁架结构修正前后参数均值及误差

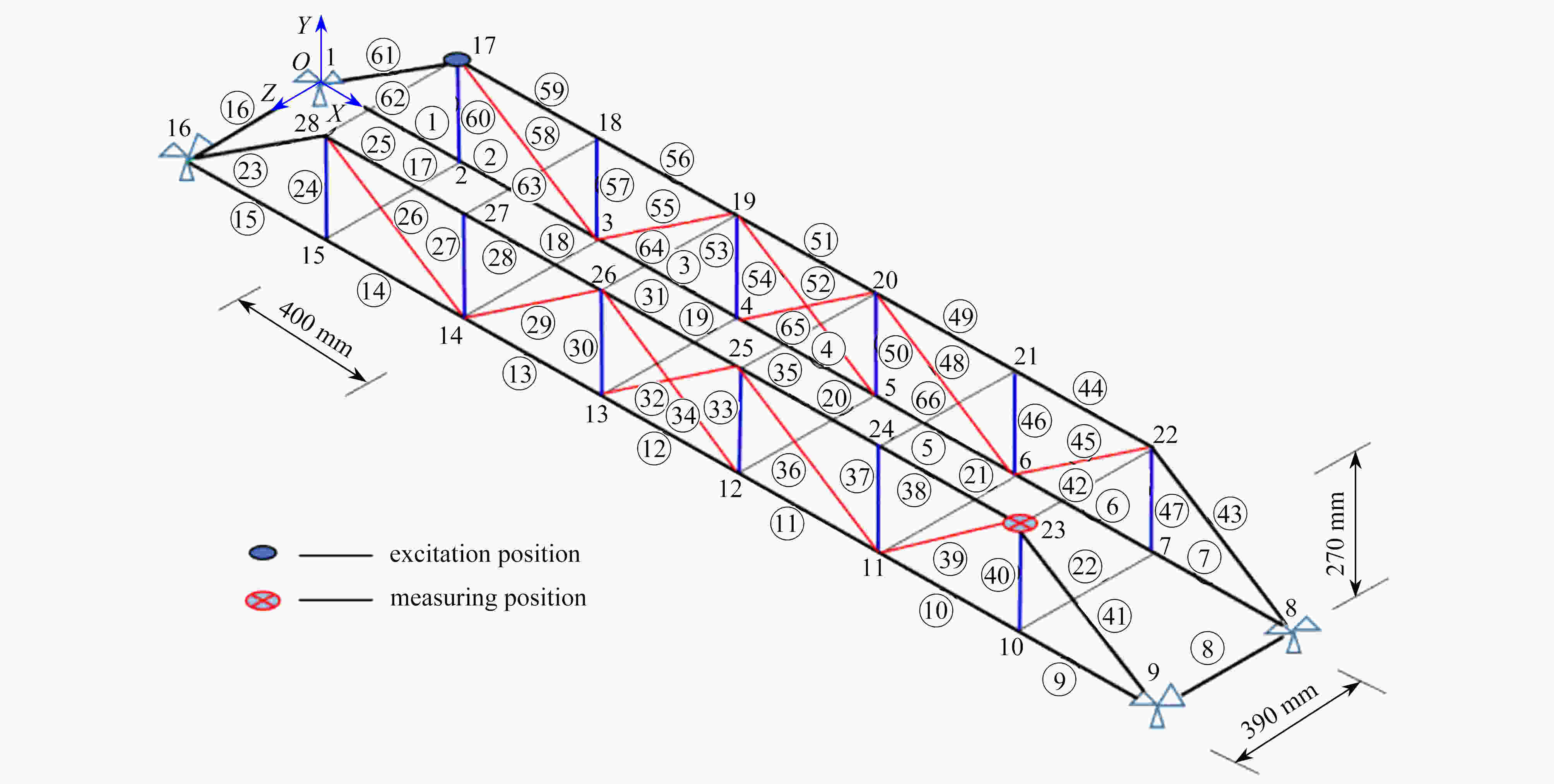
Table 3. Parameter mean values and errors of the truss structure before and after updating

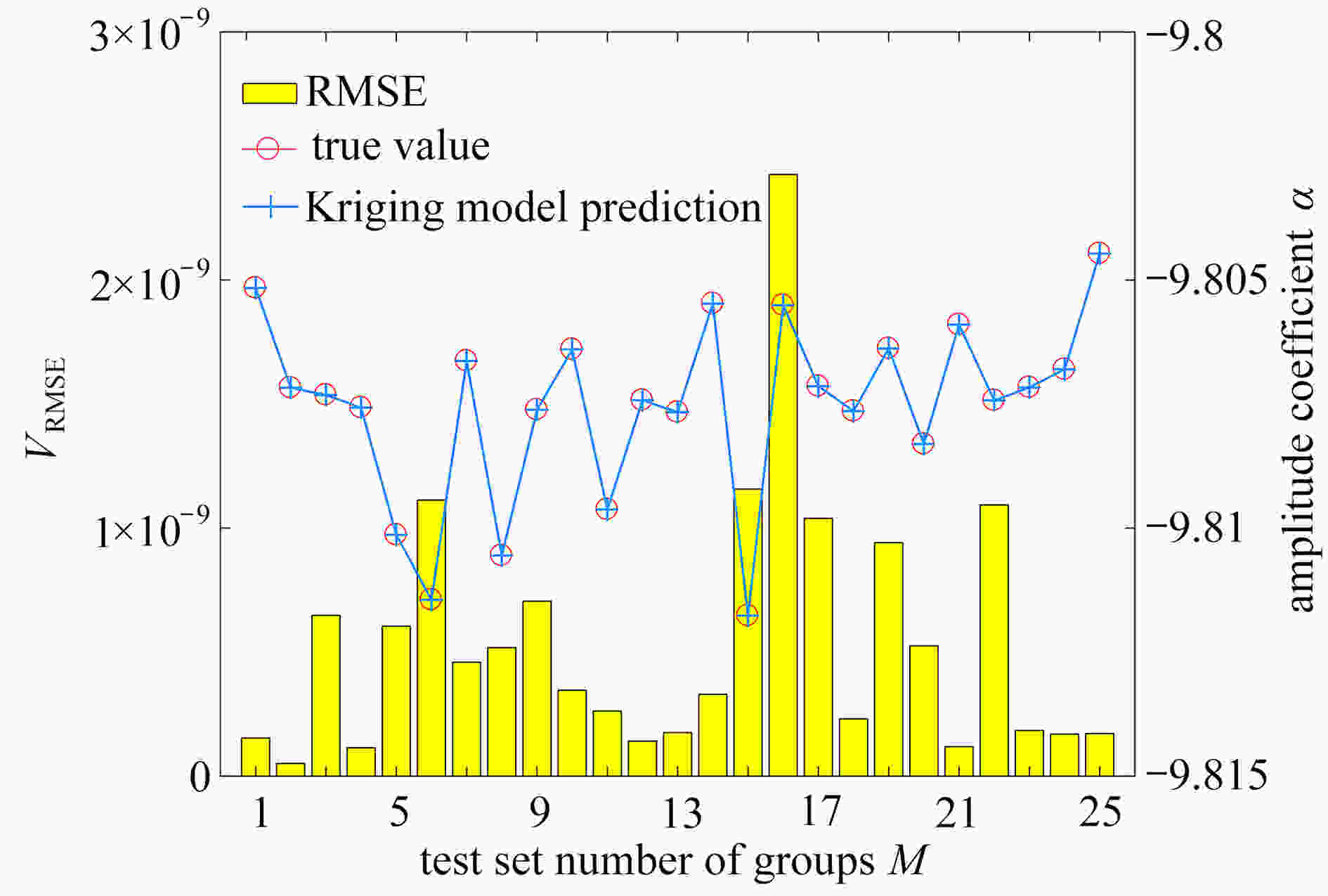
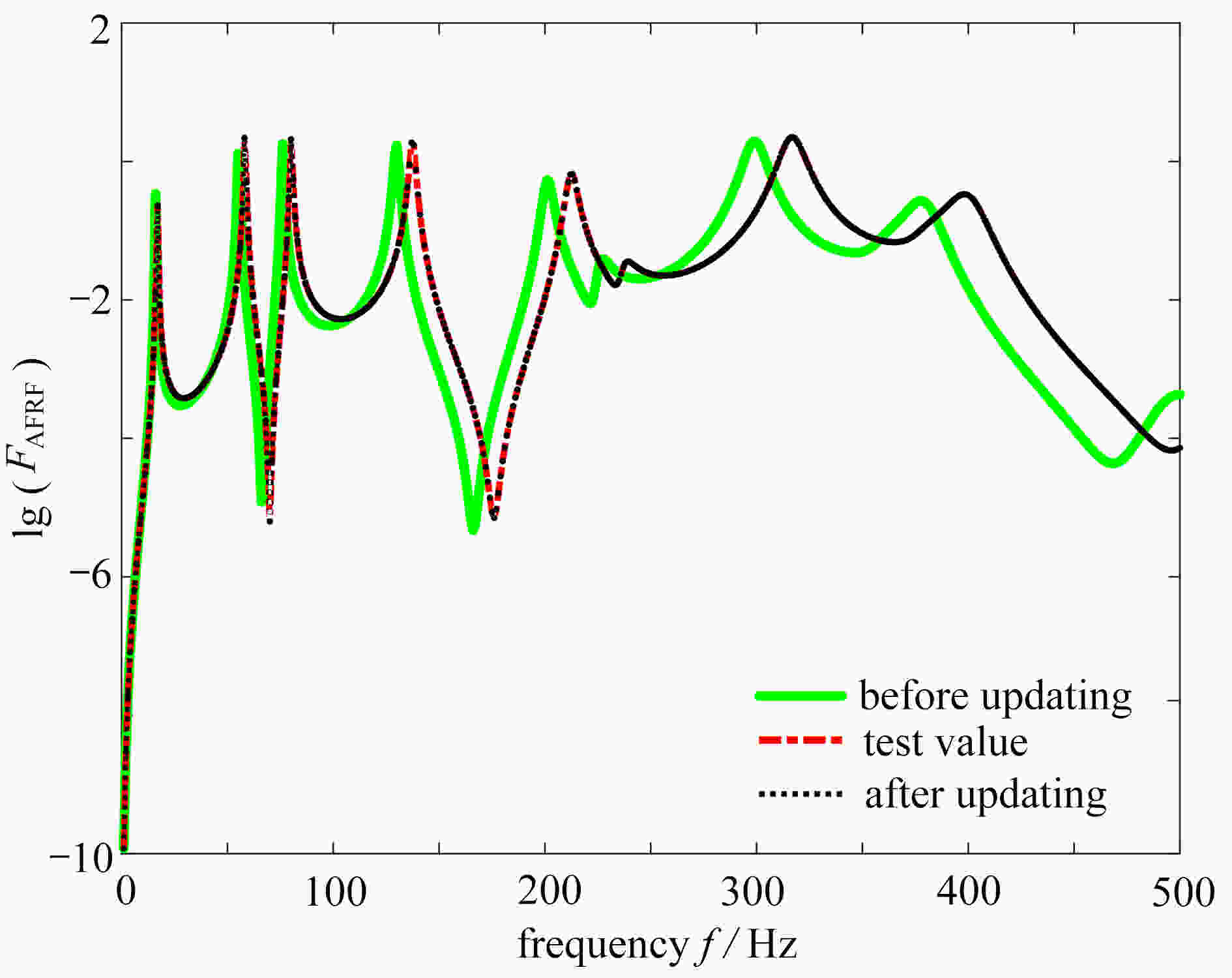
updated parameter	test value	finite element value	updated value	relative error δ/%
E_㉓/GPa	190	171	189.881	0.0626
E_⑱/GPa	190	209	190.009	0.0047
E_㉒/GPa	190	171	189.937	0.0331
E_⑫/GPa	190	209	189.971	0.0155

下载: 导出CSV

表 4 不同响应指标下的结果对比

Table 4. Comparison of results under different response indicators

response indicator	relative error of E_㉓ δ₁/%	relative error of E_⑱ δ₂/%	relative error of E_㉒ δ₃/%	relative error of E_⑫ δ₄/%	time consumed t/s
AFRF	1.8092	1.8907	0.9921	0.7739	92
approximate coefficient	0.0626	0.0047	0.0331	0.0155	27

下载: 导出CSV

表 5 桁架结构修正前后结构参数均值及误差

Table 5. Parameter mean values and errors of the truss structure before and after updating

updated parameter	test value	finite element value	updated value	relative error δ/%
E/GPa	190	209	189.607	0.207
$\rho /({\text{kg} } \cdot { {\text{m} }^{ { { - 3} } } })$	7800	7020	7773.562	0.339
A/mm²	85.5	95	85.662	0.189

下载: 导出CSV

参考文献(19)

[1]	张皓, 李东升, 李宏男. 有限元模型修正研究进展: 从线性到非线性[J]. 力学进展, 2019, 49: 542-575. (ZHANG Hao, LI Dongsheng, LI Hongnan. Recent progress on finite element model updating: from linearity to nonlinearity[J]. Advances in Mechanics, 2019, 49: 542-575.(in Chinese) ZHANG Hao, LI Dongsheng, LI Hongnan. Recent progress on finite element model updating: from linearity to nonlinearity[J]. Advances in Mechanics, 2019, 49: 542-575. (in Chinese))
[2]	STEENACKERS G, GUILLAUME P. Finite element model updating taking into account the uncertainty on the modal parameters estimates[J]. Journal of Sound and Vibration, 2006, 296(4/5): 919-934. doi: 10.1016/j.jsv.2006.03.023
[3]	TSHILIDZI M. Finite-Element-Model Updating Using Computional Intelligence Techniques[M]. London: Springer, 2010.
[4]	方圣恩, 林友勤, 夏樟华. 考虑结构参数不确定性的随机模型修正方法[J]. 振动、测试与诊断, 2014, 34(5): 832-837, 973. (FANG Sheng’en, LIN Youqin, XIA Zhanghua. Stochastic model updating method considering the uncertainties of structural parameters[J]. Journal of Vibration, Measurement and Diagnosis, 2014, 34(5): 832-837, 973.(in Chinese) doi: 10.3969/j.issn.1004-6801.2014.05.008 FANG Shengen, LIN Youqin, XIA Zhanghua. Stochastic model updating method considering the uncertainties of structural parameters[J]. Journal of Vibration Measurement and Diagnosis, 2014, 34(5): 832-837, 973. (in Chinese)) doi: 10.3969/j.issn.1004-6801.2014.05.008
[5]	DENG Z M, BI S F, SEZ A. Stochastic model updating using distance discrimination analysis[J]. Chinese Journal of Aeronautics, 2014, 27(5): 1188-1198. doi: 10.1016/j.cja.2014.08.008
[6]	万华平, 任伟新, 黄天立. 基于贝叶斯推理的随机模型修正方法[J]. 中国公路学报, 2016, 29(4): 67-76, 95. (WAN Huaping, REN Weixin, HUANG Tianli. Stochastic model updating approach by using Bayesian inference[J]. China Journal of Highway and Transport, 2016, 29(4): 67-76, 95.(in Chinese) doi: 10.3969/j.issn.1001-7372.2016.04.009 WAN Huaping, REN Weixin, HUANG Tianli. Stochastic model updating approach by using Bayesian inference[J]. China Journal of Highway and Transport, 2016, 29(4): 67-76, 95. (in Chinese)) doi: 10.3969/j.issn.1001-7372.2016.04.009
[7]	ZHAI X, FEI C W, CHOY Y S, et al. A stochastic model updating strategy-based improved response surface model and advanced Monte Carlo simulation[J]. Mechanical Systems and Signal Processing, 2017, 82: 323-338. doi: 10.1016/j.ymssp.2016.05.026
[8]	陈喆, 何欢, 陈国平, 等. 考虑不确定性因素的有限元模型修正方法研究[J]. 振动工程学报, 2017, 30(6): 921-928. (CHEN Zhe, HE Huan, CHEN Guoping, et al. The research of finite element model updating method considering the uncertainty[J]. Journal of Vibration Engineering, 2017, 30(6): 921-928.(in Chinese) CHEN Zhe, HE Huan, CHEN Guoping, et al. The research of finite element model updating method considering the uncertainty[J]. Journal of Vibration Engineering, 2017, 30(6): 921-928. (in Chinese))
[9]	JALALI H, KHODAPARAST H H, MADINEI H, et al. Stochastic modelling and updating of a joint contact interface[J]. Mechanical Systems and Signal Processing, 2019, 129: 645-658. doi: 10.1016/j.ymssp.2019.04.003
[10]	ZHAO Y L, DENG Z M, ZHANG X J. A robust stochastic model updating method with resampling processing[J]. Mechanical Systems and Signal Processing, 2020, 136: 106494. doi: 10.1016/j.ymssp.2019.106494
[11]	邓振鸿, 张保强, 苏国强, 等. 基于近似似然的频响函数不确定性模型修正[J]. 振动、测试与诊断, 2020, 40(3): 548-554, 628. (DENG Zhenhong, ZHANG Baoqiang, SU Guoqiang, et al. Uncertainty model updating of frequency response function based on approximate likelihood function[J]. Journal of Vibration, Measurement and Diagnosis, 2020, 40(3): 548-554, 628.(in Chinese) DENG Zhenhong, ZHANG Baoqiang, SU Guoqiang, et al. Uncertainty model updating of frequency response function based on approximate likelihood function[J]. Journal of Vibration, Measurement and Diagnosis, 2020, 40(3): 548-554, 628. (in Chinese))
[12]	韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. (HAN Zhonghua. Kriging surrogate model and its application to design optimization: a review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225.(in Chinese) HAN Zhonghua. Kriging surrogate model and its application to design optimization: A review of recent progress[J]. Acta Aeronautica ET Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese))
[13]	ARORA S, SINGH S. Butterfly optimization algorithm: a novel approach for global optimization[J]. Soft Computing, 2018, 23(3): 715-734.
[14]	宋国明, 王厚军, 刘红, 等. 基于提升小波变换和SVM的模拟电路故障诊断[J]. 电子测量与仪器学报, 2010, 24(1): 17-22. (SONG Guoming, WANG Houjun, LIU Hong, et al. Analog circuit fault diagnosis using lifting wavelet transform and SVM[J]. Journal of Electronic Measurement and Instrument, 2010, 24(1): 17-22.(in Chinese) doi: 10.3724/SP.J.1187.2010.00017 SONG Guoming, WANG Houjun, LIU Hong, et al. Analog circuit fault diagnosis using lifting wavelet transform and SVM[J]. Journal of Electronic Measurement And Instrument, 2010, 24(1): 17-22. (in Chinese)) doi: 10.3724/SP.J.1187.2010.00017
[15]	SWELDENS W. The lifting scheme: a construction of second generation wavelets[J]. SIAM Journal on Mathematical Analysis, 1998, 29(2): 511-546. doi: 10.1137/S0036141095289051
[16]	PANARETOS V M, YOAV ZEMEL Y. Statistical aspects of Wasserstein distances[J]. Annual Review of Statistics and Its Application, 2019, 6(1): 405-431. doi: 10.1146/annurev-statistics-030718-104938
[17]	周平, 赵向志. 面向建模误差PDF形状与趋势拟合优度的动态过程优化建模[J]. 自动化学报, 2021, 47(10): 2402-2411. (ZHOU Ping, ZHAO Xiangzhi. Optimized modeling of dynamic process oriented towards modeling error PDF shape and goodness of fit[J]. Acta Automatica Sinica, 2021, 47(10): 2402-2411.(in Chinese) ZHOU Ping, ZHAO Xiangzhi. Optimized modeling of dynamic process oriented towards modeling error pdf shape and goodness of fit[J]. Acta Automatica Sinica, 2021, 47(10): 2402-2411. (in Chinese))
[18]	肖先勇, 桂良宇, 李成鑫, 等. 基于Wasserstein距离的多电压暂降事件同源检测方法[J]. 电网技术, 2020, 44(12): 4684-4693. (XIAO Xianyong, GUI Liangyu, LI Chengxin, et al. Multiple voltage sag events homology detection based on Wasserstein distance[J]. Power System Technology, 2020, 44(12): 4684-4693.(in Chinese) XIAO Xianyong, GUI Liangyu, LI Chengxin, et al. Multiple voltage sag events homology detection based on Wasserstein distance[J]. Power System Technology, 2020, 44(12): 4684-4693. (in Chinese))
[19]	SEYEDALI M, ANDREW L. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95(5): 51-67.