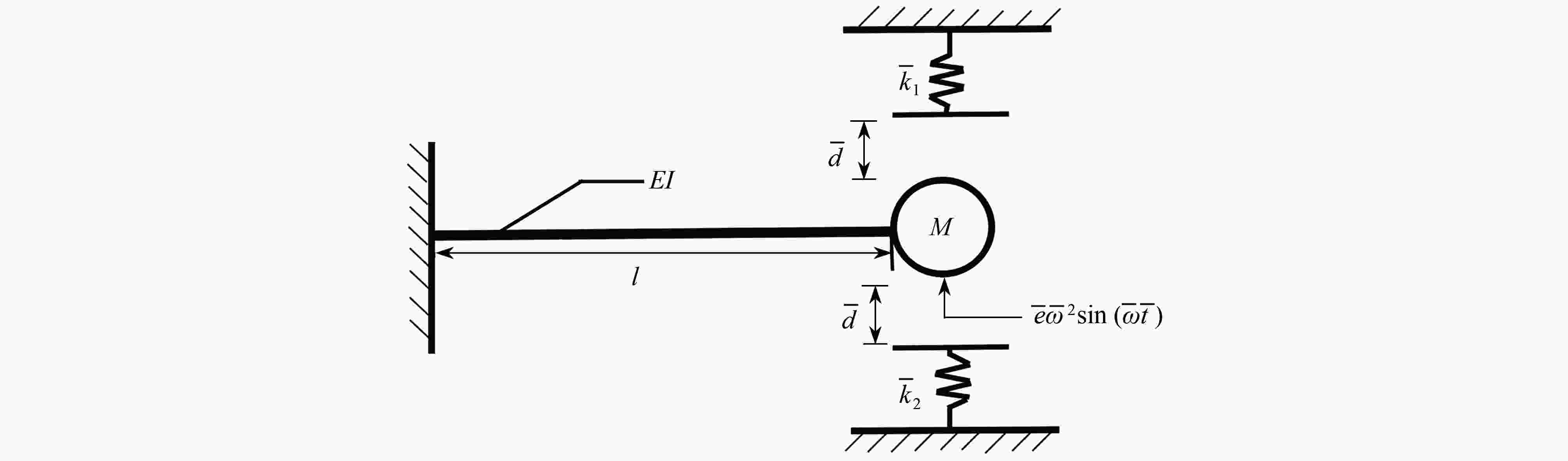
Non-Smooth Grazing Dynamics for Cantilever Beams With Bilateral Elastic Constraints
-
摘要:
研究了具有双侧弹性约束的单自由度悬臂梁系统擦边诱导的非光滑动力学行为。首先，基于弹性碰撞悬臂梁的动力学方程和擦边点的定义，分析了双侧擦边周期运动的存在性条件。其次，选取零速度的Poincaré截面，推导了双侧擦边轨道附近带参数的高阶不连续映射。然后，结合光滑流映射和高阶不连续映射建立了新的复合分段范式映射。最后，将基于低阶范式映射和高阶范式映射得到的分岔图进行对比，分析验证了高阶范式映射的有效性，并通过数值仿真进一步揭示了弹性碰撞悬臂梁的擦边动力学。
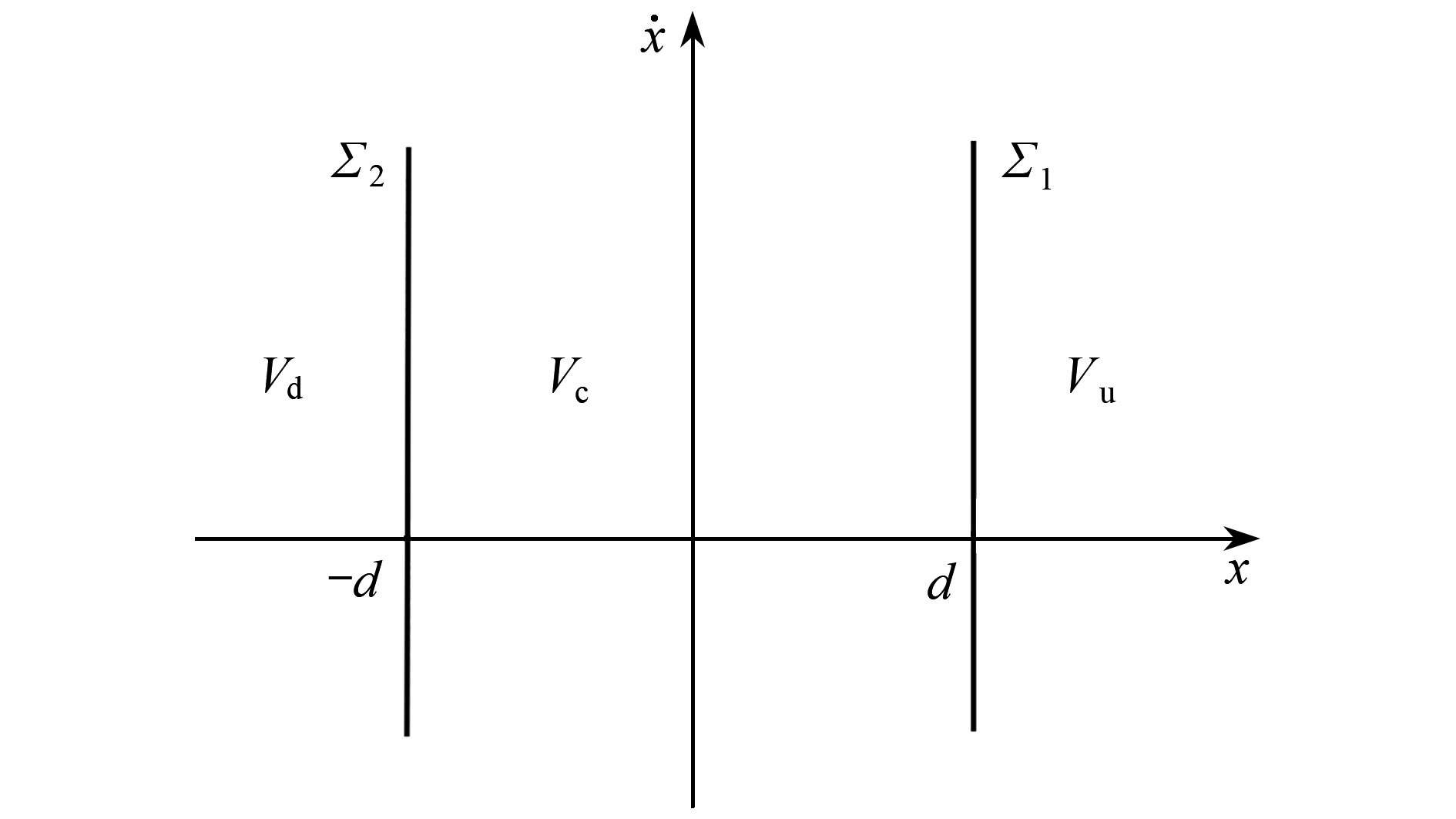
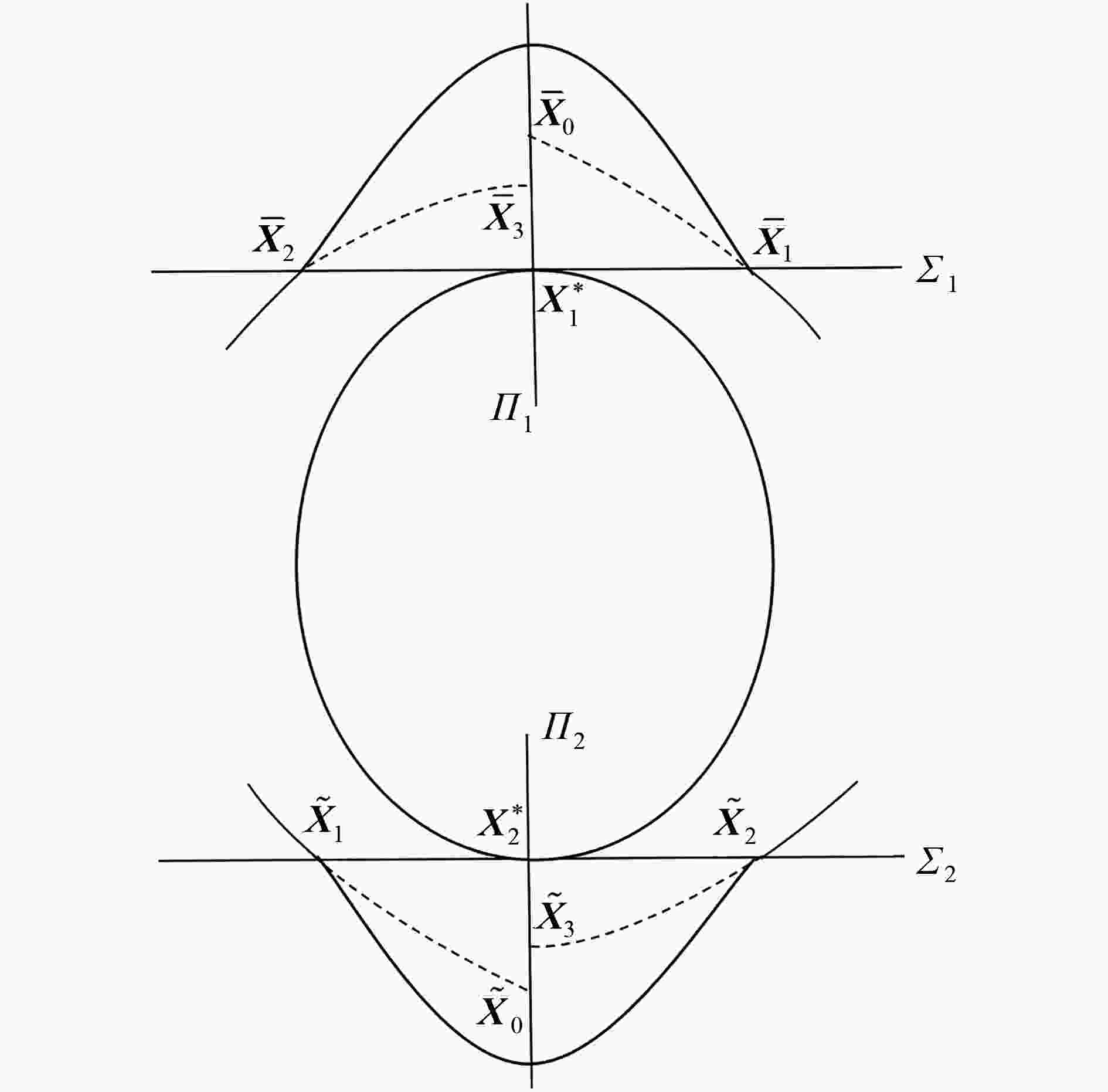
Abstract:The grazing-induced non-smooth dynamical behaviors of single-degree-of-freedom cantilever beam systems with bilateral elastic constraints were studied. Firstly, based on the dynamical equations for the cantilever beam under elastic impacts and the definition of grazing points, the existence condition for the bilateral grazing periodic motion was analyzed. Secondly, the zero-velocity Poincaré section was selected to derive the high-order discontinuous mapping with parameters near bilateral grazing orbits. Then a new composite piecewise normal form mapping was established through combination of the smooth flow mapping and the high-order discontinuous mapping. Finally, the validity of the high-order mapping was verified through comparison of the bifurcation diagram of the low-order mapping with that of the high-order mapping, and the grazing dynamics of the cantilever beam under elastic impacts were further revealed through numerical simulation.
-
图 1 双侧弹性碰撞悬臂梁系统模型
Figure 1. The cantilever beam system under bilateral elastic impacts
图 2 弹性碰撞悬臂梁系统 (2) 的二维相平面
Figure 2. The 2D phase plane of the cantilever beam system under bilateral elastic impacts (2)
图 3 擦边点附近不连续映射
${\boldsymbol{P}}_ {\rm{PDM1}}$ 和${\boldsymbol{P}}_ {\rm{PDM2}}$ 的示意图Figure 3. The schematic diagram of the discontinuity mappings
${\boldsymbol{P}}_ {\rm{PDM1}}$ and${\boldsymbol{P}}_ {\rm{PDM2}}$ near grazing points
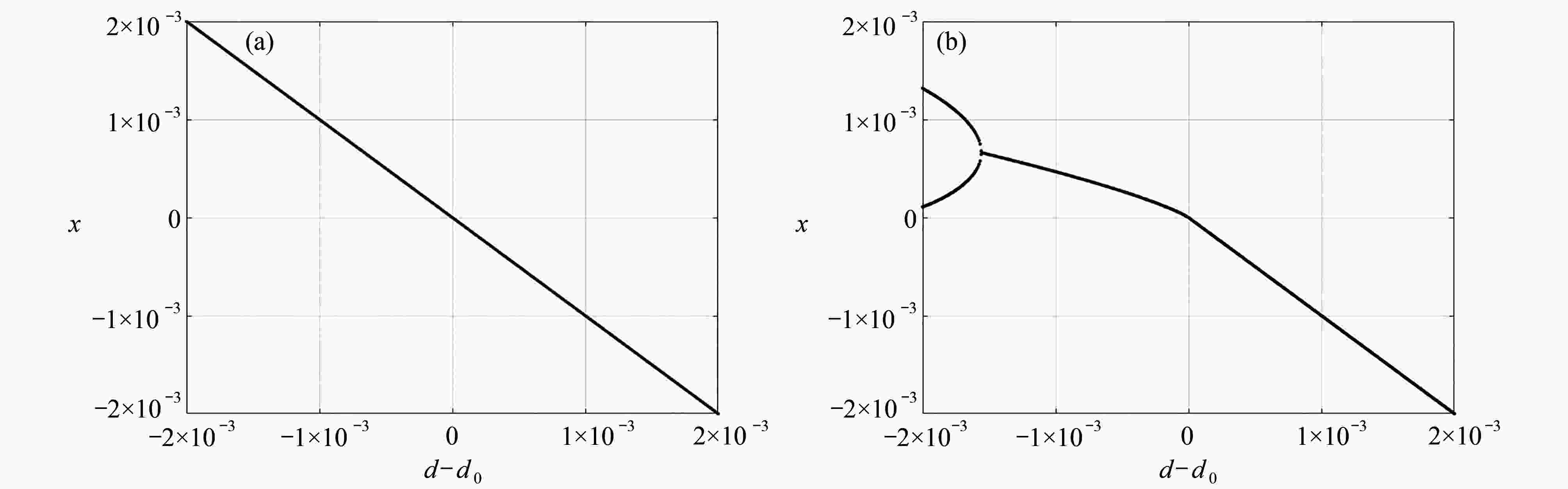
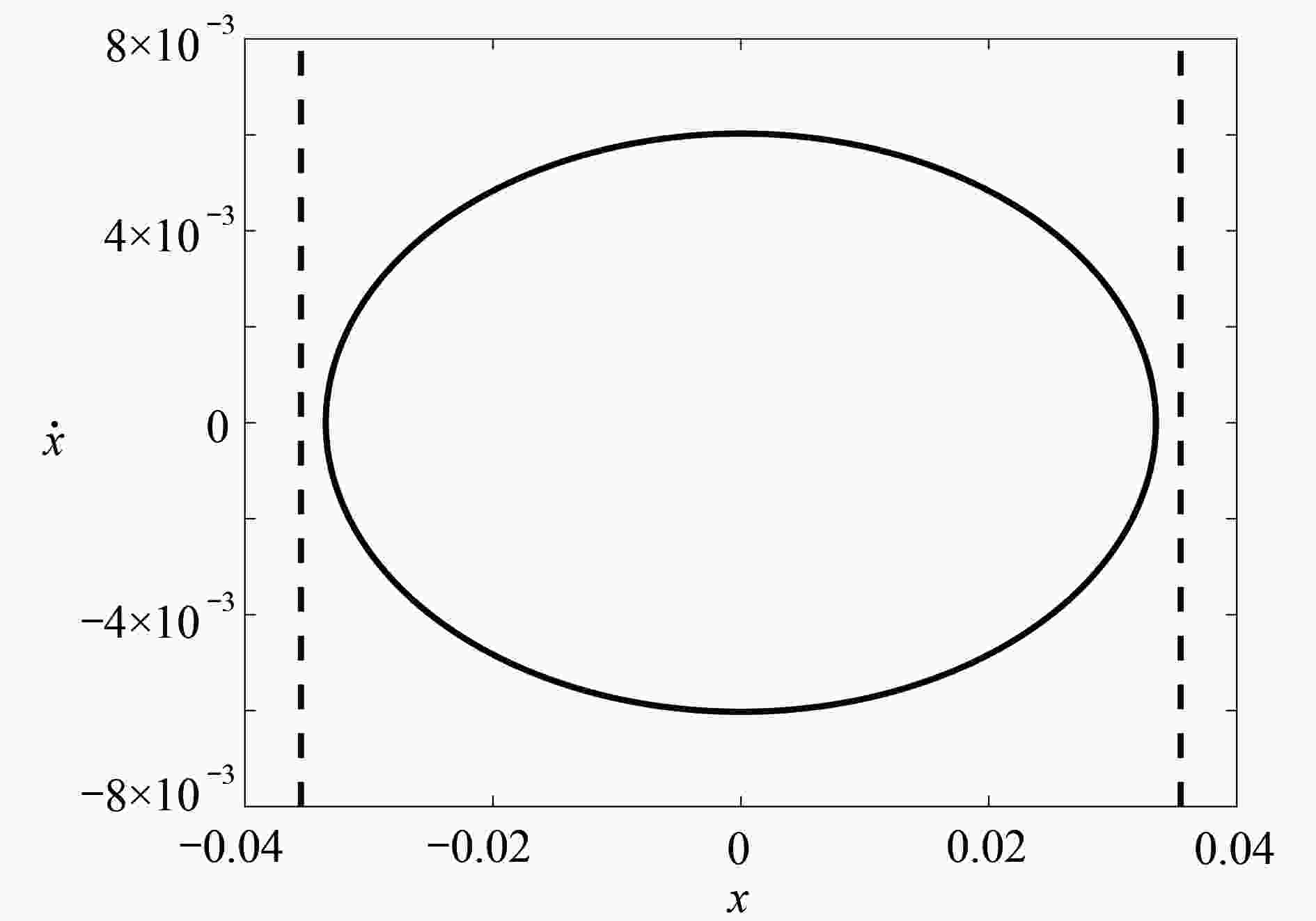
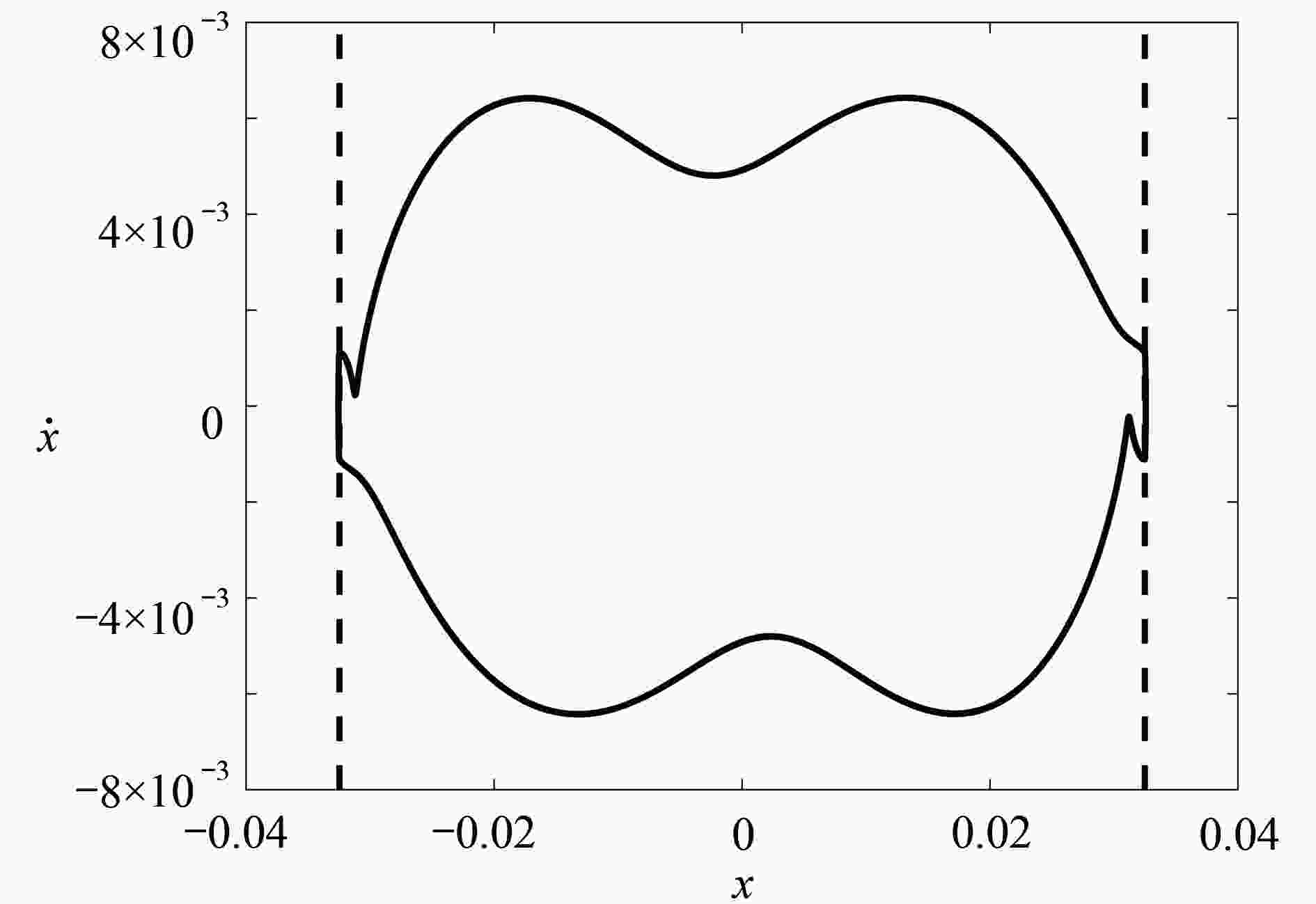
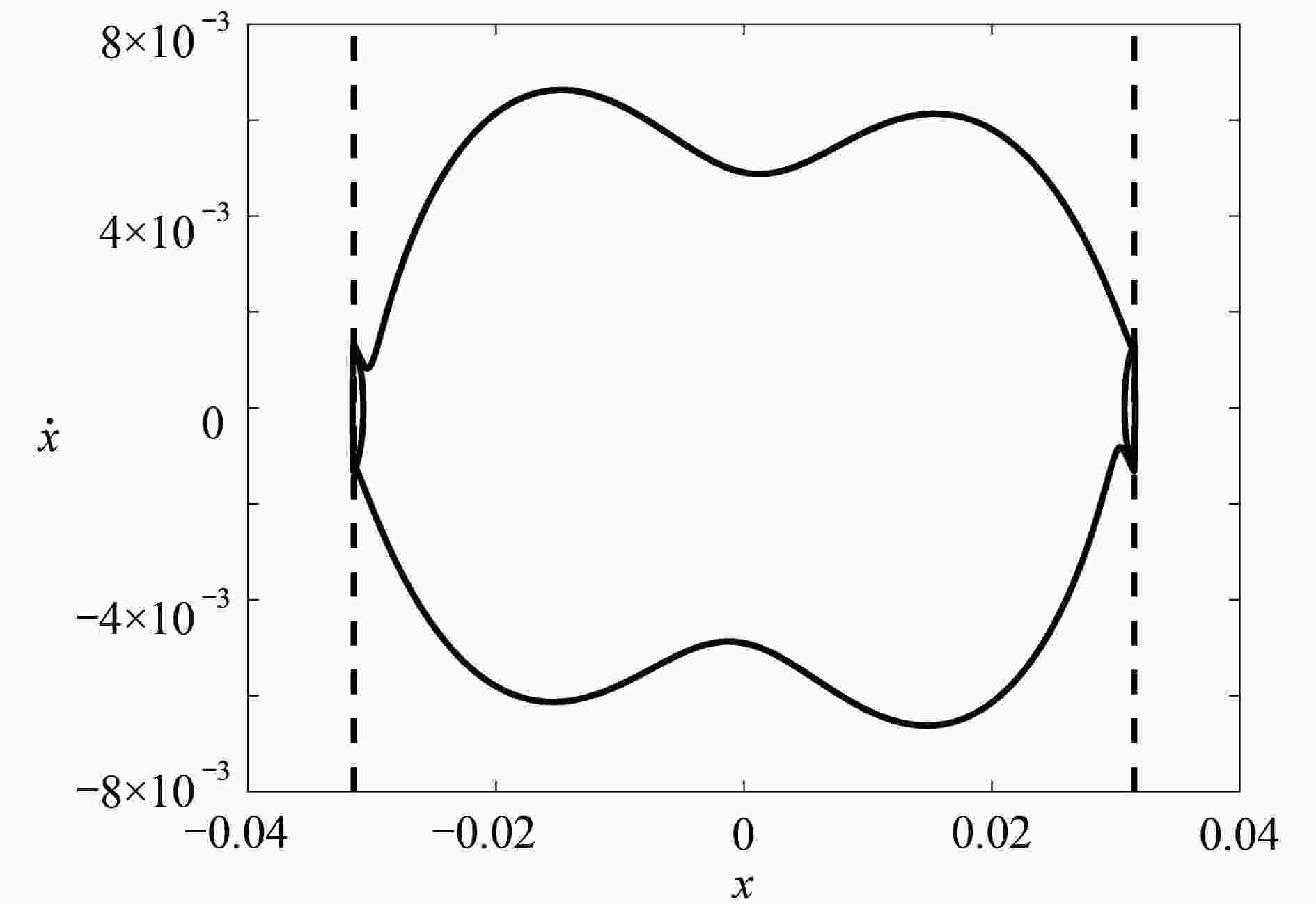
图 4 系统 (2) 擦边轨道附近的分岔图：(a) 基于低阶映射 (43) 得到的擦边轨道附近的分岔图；(b) 基于高阶映射 (49) 得到的擦边轨道附近的分岔图
Figure 4. The bifurcation diagram of system (2) near the grazing orbit: (a) the bifurcation diagram near the grazing orbit obtained based on low-order mapping (43); (b) the bifurcation diagram near the grazing orbit obtained based on high-order mapping (49)
图 5 在
$ d=d_{0}+0.002\; $ 处的非碰撞单周期运动Figure 5. The non-impact single periodic motion at
$ d=d_{0}+0.002\; $ 
图 6 在
$ d=d_{0}\; $ 处的双擦边周期运动Figure 6. The double grazing periodic motion at
$ d=d_{0}\; $ 
图 7 在
$ d=d_{0}-0.001\; $ 处的 1-1-1 碰撞周期运动Figure 7. The 1-1-1 impact periodic motion at
$ d=d_{0}-0.001\; $ -
[1] NORDMARK A B. Non-periodic motion caused by grazing incidence in an impact oscillator[J]. Journal of Sound and Vibration, 1991, 145(2): 279-297.NORDMARK A B. Non-periodic motion caused by grazing incidence in an impact oscillator[J]. Journal of Sound and Vibration, 1991, 145(2): 279-297. [2] CHIN W, OTT E, NUSEE H E, et al. Grazing bifurcations in impact oscillators[J]. Physical Review E, 1994, 50(6): 4427-4444.CHIN W, OTT E, NUSEE H E, et al. Grazing bifurcations in impact oscillators[J]. Physical Review E, 1994, 50(6): 4427-4444. [3] LAMBA H, BUDD C J. Scaling of Lyapunov exponents at nonsmooth bifurcations[J]. Physical Review E, 1994, 50(1): 84-90.LAMBA H, BUDD C J. Scaling of Lyapunov exponents at nonsmooth bifurcations[J]. Physical Review E, 1994, 50(1): 84-90. [4] FREDRIKSSON M H, NORDMARK A B. Bifurcations caused by grazing incidence in many degrees of freedom impact oscillators[J]. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, 1997, 453(1961): 1261-1276.FREDRIKSSON M H, NORDMARK A B. Bifurcations caused by grazing incidence in many degrees of freedom impact oscillators[J]. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, 1997, 453(1961): 1261-1276. [5] LI Q H, WEI L M, AN J Y, et al. Double grazing periodic motions and bifurcations in a vibro-impact system with bilateral stops[J]. Hindawi Publishing Corporation Abstract and Applied Analysis, 2014: 1-9.LI Q H, WEI L M, AN J Y, et al. Double grazing periodic motions and bifurcations in a vibro-impact system with bilateral stops[J]. Abstract and Applied Analysis, 2014, 2014: 642589. [6] XU J Q, CHEN P, LI Q H. Theoretical analysis of co-dimension-two grazing bifurcations in n-degree-of-freedom impact oscillator with symmetrical constrains[J]. Nonlinear Dynamics, 2015, 82: 1641-1657.XU J Q, CHEN P, LI Q H. Theoretical analysis of co-dimension-two grazing bifurcations in n-degree-of-freedom impact oscillator with symmetrical constrains[J]. Nonlinear Dynamics, 2015, 82: 1641-1657. [7] WEGER J D, WILLEM V D W, MOLENAAR J. Grazing impact oscillations[J]. Physical Review E, 2000, 62(2): 2030.WEGER J D, WILLEM V D W, MOLENAAR J. Grazing impact oscillations[J]. Physical Review E, 2000, 62(2): 2030. [8] MOLENAAR J, WEGER J D, WILLEM V D W. Mappings of grazing-impact oscillators[J]. Nonlinearity, 2001, 14(2): 301-321.MOLENAAR J, WEGER J D, WILLEM V D W. Mappings of grazing-impact oscillators[J]. Nonlinearity, 2001, 14(2): 301-321. [9] ZHAO X P. Discontinuity mapping for near-grazing dynamics in vibro-impact oscillators[J]. Vibro-Impact Dynamics of Ocean Systems and Related Problems, 2009, 44: 275-285.ZHAO X P. Discontinuity mapping for near-grazing dynamics in vibro-impact oscillators[J]. Vibro-Impact Dynamics of Ocean Systems and Related Problems, 2009, 44: 275-285. [10] YIN S, WEN G L, XU H D, et al. Higher order zero time discontinuity mapping for analysis of degenerate grazing bifurcations of impacting oscillators[J]. Journal of Sound and Vibration, 2018, 437: 209-222.YIN S, WEN G L, XU H D, et al. Higher order zero time discontinuity mapping for analysis of degenerate grazing bifurcations of impacting oscillators[J]. Journal of Sound and Vibration, 2018, 437: 209-222. [11] CZOLCZYNSKI K, OKOLEWSKI A, BLAZEJCZK-OKOLEWSKA B. Lyapunov exponents in discrete modelling of a cantilever beam impacting on a moving base[J]. International Journal of Non-Linear Mechanics, 2017, 88: 74-84.CZOLCZYNSKI K, OKOLEWSKI A, BLAZEJCZK-OKOLEWSKA B. Lyapunov exponents in discrete modelling of a cantilever beam impacting on a moving base[J]. International Journal of Non-Linear Mechanics, 2017, 88: 74-84. [12] BLAZEJCZK-OKOLEWSKA B, CZOLCZYNSKI K, KAPITANIAK T. Dynamics of a two-degree-of-freedom cantilever beam with impacts[J]. Chaos, Solitons and Fractals, 2009, 40(4): 1991-2006.BLAZEJCZK-OKOLEWSKA B, CZOLCZYNSKI K, KAPITANIAK T. Dynamics of a two-degree-of-freedom cantilever beam with impacts[J]. Chaos, Solitons and Fractals, 2009, 40(4): 1991-2006. -
下载:
计量
- 文章访问数: 506
- HTML全文浏览量: 305
- PDF下载量: 48
- 被引次数: 0
渝公网安备50010802005915号