基于变体积约束的阻尼材料微结构拓扑优化研究

张东东; 栾福强; 赵礼辉; 郑玲

doi:10.21656/1000-0887.420206

基于变体积约束的阻尼材料微结构拓扑优化研究

doi: 10.21656/1000-0887.420206

张东东^{1, 2, ,},
栾福强¹,
赵礼辉^{1, 2},
郑玲³

1.
上海理工大学机械工程学院，上海 200093
2.
上海市新能源汽车可靠性评价公共技术平台，上海 200093
3.
重庆大学机械与运载工程学院，重庆 400044

基金项目: 上海市青年科技英才扬帆计划（18YF1418500）

详细信息

作者简介:
张东东（1986—），男，副教授，博士，硕士生导师（通讯作者. E-mail：dongdongzhang@usst.edu.cn）

中图分类号: TB53
计量
- 文章访问数: 580
- HTML全文浏览量: 427
- PDF下载量: 55
- 被引次数: 0
出版历程
- 收稿日期: 2021-07-06
- 修回日期: 2021-11-27
- 网络出版日期: 2022-05-26
- 刊出日期: 2022-06-30

Research on Topology Optimization of Damping Material Microstructures With Varied Volume Constraints

ZHANG Dongdong^{1, 2
, ,},
LUAN Fuqiang¹,
ZHAO Lihui^{1, 2},
ZHENG Ling³

1.
School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, P.R.China
2.
Shanghai Technology Service Platform of Reliability Evaluation for New Energy Vehicles, Shanghai 200093, P.R.China
3.
College of Mechanical and Vehicle Engineering, Chongqing University, Chongqing 400044, P.R.China

摘要

摘要:
阻尼复合结构的抑振性能取决于材料布局和阻尼材料特性。该文提出了一种变体积约束的阻尼材料微结构拓扑优化方法，旨在以最小的材料用量获得具有期望性能的阻尼材料微结构。基于均匀化方法，建立阻尼材料三维微结构有限元模型，得到阻尼材料的等效弹性矩阵。逆用Hashin-Shtrikman界限理论，估计对应于期望等效模量的阻尼材料体积分数限，并构建阻尼材料体积约束限的移动准则。将获得阻尼材料微结构期望性能的优化问题转化为体积约束下最大化等效模量的优化问题，建立阻尼材料微结构的拓扑优化模型。利用优化准则法更新设计变量，实现最小材料用量下的阻尼材料微结构最优拓扑设计。通过典型数值算例验证了该方法的可行性和有效性，并讨论了初始微构型、网格依赖性和弹性模量等对阻尼材料微结构的影响。
- 阻尼材料 /
- 变体积约束 /
- 等效模量 /
- 均匀化方法 /
- Hashin-Shtrikman界限理论
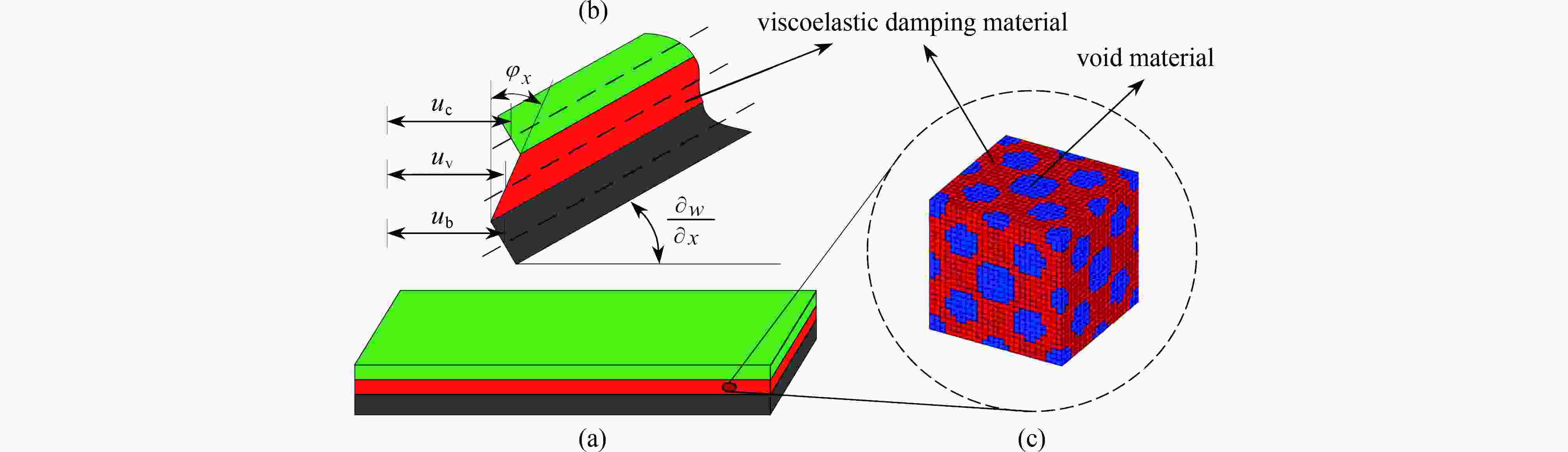
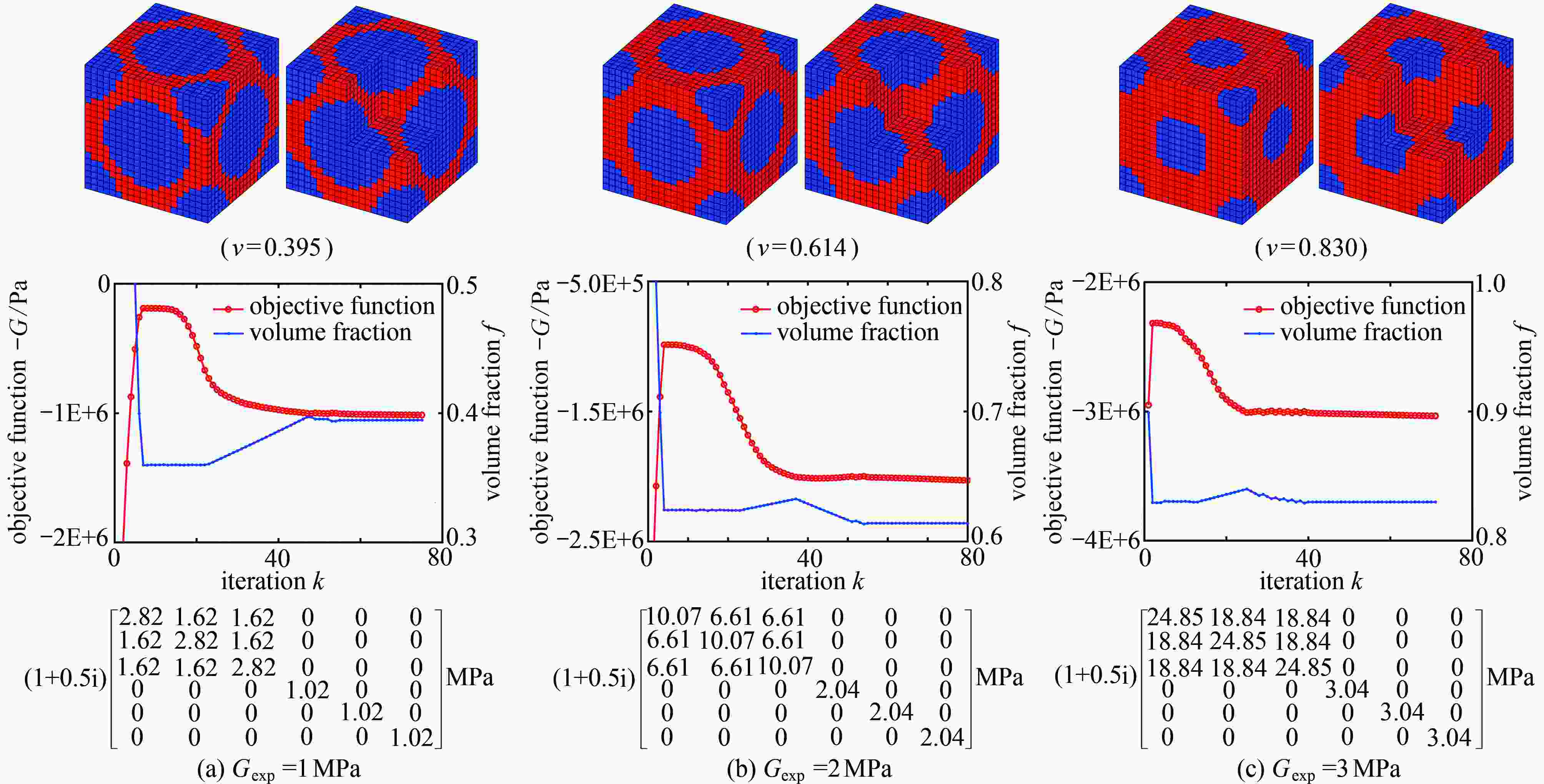
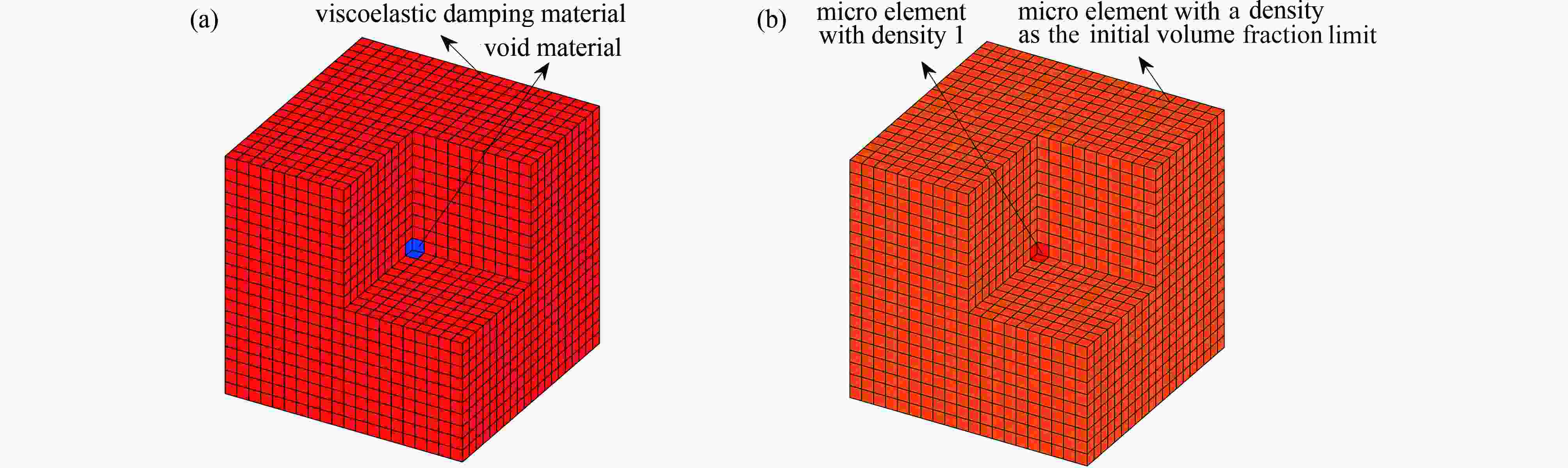
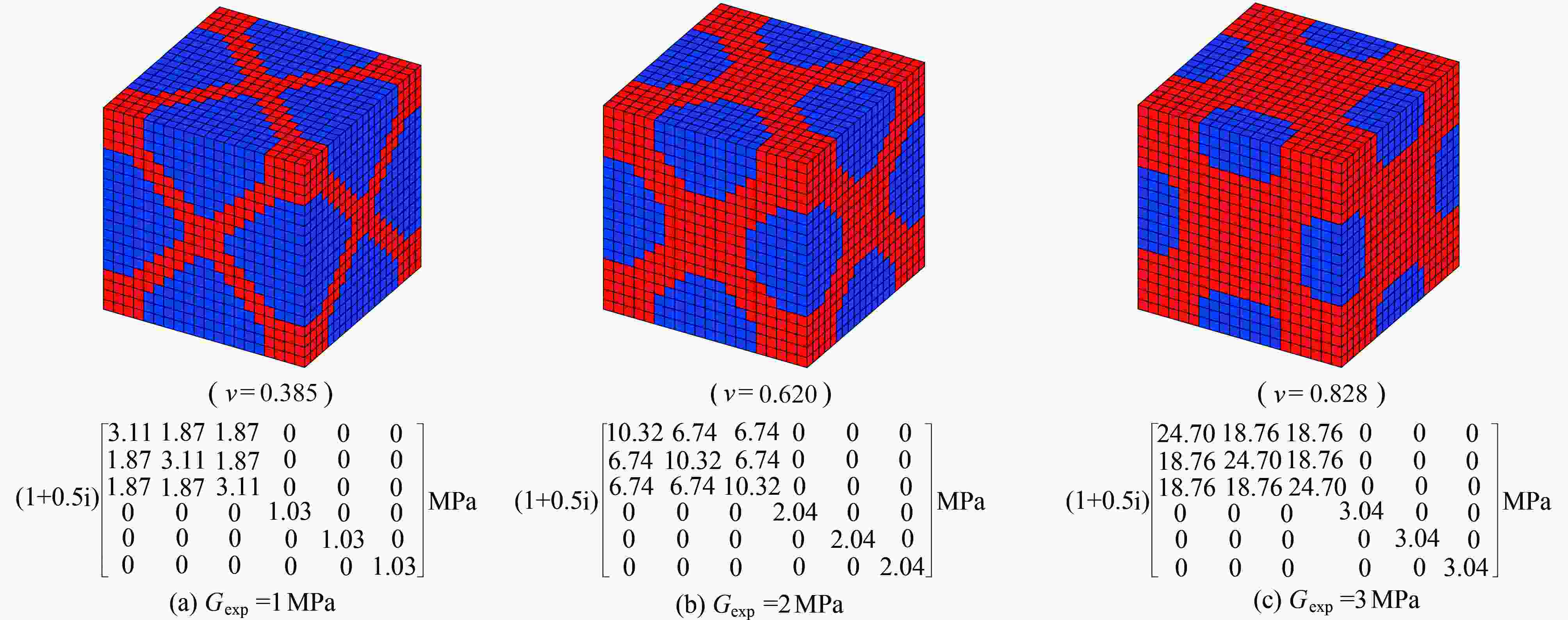
Abstract:
The vibration suppression performance of a damping composite structure depends on the material layout and the damping material properties. A topology optimization method was proposed for damping material microstructures with varied volume constraints, to obtain the damping material microstructure with desired properties under the smallest material consumption. Based on the homogenization method, a 3D finite element model for the damping material was established, and the effective elastic matrix of the damping material was formulated. The Hashin-Shtrikman bounds theory was used inversely to estimate the volume fraction bound of the damping material corresponding to the desired effective modulus, and a movement criterion for volume constraint bounds of damping materials was constructed. Then the optimization problem of achieving the desired properties of damping materials with microstructures was converted to another problem of maximizing the desired modulus under volume constraints, and a topology optimization model for the damping material microstructure was established. The optimality criteria method was employed to update the design variables, and the optimized topology configurations of damping material microstructures were obtained. The feasibility and effectiveness of the proposed method were verified with several numerical examples, and the influences of the initial configurations, the mesh density and Young’s modulus on the microstructure configurations of the damping material were also discussed.
- damping material /
- varied volume constraint /
- effective modulus /
- homogenization method /
- Hashin-Shtrikman bounds theory

HTML全文

图 1 含阻尼材料微结构的夹层阻尼结构示意图：(a) 夹层阻尼结构；(b)阻尼材料变形图；(c)阻尼材料三维微结构

Figure 1. Schematic drawings of a sandwich damping structure with a damping core microstructure: (a) the sandwich damping structure; (b) the deformation of the damping core; (c) the 3D microstructure of the damping core

下载: 全尺寸图片幻灯片

图 2 阻尼材料单胞初始构型A

Figure 2. Initial configuration A of the damping material unit cell

下载: 全尺寸图片幻灯片

图 3 基于初始构型A获得阻尼材料单胞微结构拓扑优化结果

Figure 3. Topology optimization results of the damping material unit cell microstructure for initial configuration A

下载: 全尺寸图片幻灯片

图 4 阻尼材料初始构型：(a) 阻尼材料初始构型B； (b) 阻尼材料初始构型C

Figure 4. The initial configurations of the damping material unit cell：(a) initial configuration B of the damping material unit cell; (b) initial configuration C of the damping material unit cell

下载: 全尺寸图片幻灯片

图 5 基于初始构型B获得阻尼材料单胞微结构拓扑优化结果

Figure 5. Topology optimization results of the damping material unit cell microstructure for initial configuration B

下载: 全尺寸图片幻灯片

图 6 基于初始构型C获得阻尼材料单胞微结构拓扑优化结果

Figure 6. Topology optimization results of the damping material unit cell microstructure for initial configuration C

下载: 全尺寸图片幻灯片

图 7 单胞初始构型A优化结果(15 × 15 × 15)

Figure 7. Topology optimization results of initial configuration A (15 × 15 × 15)

下载: 全尺寸图片幻灯片

图 8 单胞初始构型A优化结果(25 × 25 × 25)

Figure 8. Topology optimization results of initial configuration A (25 × 25 × 25)

下载: 全尺寸图片幻灯片

图 9 单胞初始构型A优化结果(30 × 30 × 30)

Figure 9. Topology optimization results of initial configuration A (30 × 30 × 30)

下载: 全尺寸图片幻灯片

图 10 基于初始构型A的拓扑优化结果(E_v=10 MPa)

Figure 10. Topology optimization results of initial configuration A (E_v=10 MPa)

下载: 全尺寸图片幻灯片

图 11 基于初始构型A的拓扑优化结果(E_v=15 MPa)

Figure 11. Topology optimization results of initial configuration A (E_v=15 MPa)

下载: 全尺寸图片幻灯片

参考文献(20)

[1]	曾昭阳, 范红伟, 焦映厚, 等. 基于三明治夹层约束阻尼结构的潜艇降噪[J]. 科学技术与工程, 2020, 20(22): 8975-8982. (ZENG Zhaoyang, FANG Hongwei, JIAO Yinghou, et al. Noise reduction of submarine based on sandwich constrained layer damping structure[J]. Science Technology and Engineering, 2020, 20(22): 8975-8982.(in Chinese) doi: 10.3969/j.issn.1671-1815.2020.22.018 ZENG Zhaoyang, FANG Hongwei, JIAO Yinghou, et al. Noise reduction of submarine based on sandwich constrained layer damping structure[J]. Science Technology and Engineering, 2020, 20(22): 8975-8982. (in Chinese)) doi: 10.3969/j.issn.1671-1815.2020.22.018
[2]	ANSARI M, KHAJEPOUR A, ESMAILZADEH E. Application of level set method to optimal vibration control of plate structures[J]. Journal of Sound and Vibration, 2013, 332(4): 687-700. doi: 10.1016/j.jsv.2012.09.006
[3]	FANG Z P, ZHENG L. Topology optimization for minimizing the resonant response of plates with constrained layer damping treatment[J]. Shock and Vibration, 2015, 2015(2): 1-11.
[4]	PANG J, ZHENG W G, YANG L, et al. Topology optimization of free damping treatments on plates using level set method[J]. Shock and Vibration, 2020, 2020: 5084167.
[5]	CHEN W J, LIU S T. Topology optimization of microstructures of viscoelastic damping materials for a prescribed shear modulus[J]. Structural and Multidisciplinary Optimization, 2014, 50(2): 287-296. doi: 10.1007/s00158-014-1049-3
[6]	YANG R Z, DU J B. Microstructural topology optimization with respect to sound power radiation[J]. Structural and Multidisciplinary Optimization, 2013, 47(2): 191-206. doi: 10.1007/s00158-012-0838-9
[7]	CHEN W J, LIU S T. Microstructural topology optimization of viscoelastic materials for maximum modal loss factor of macrostructures[J]. Structural and Multidisciplinary Optimization, 2016, 53(1): 1-14. doi: 10.1007/s00158-015-1305-1
[8]	FANG Z P, LEI Y, TIAN S X, et al. Microstructural topology optimization of constrained layer damping on plates for maximum modal loss factor of macrostructures[J]. Shock and Vibration, 2020, 2020: 8837610.
[9]	ANDREASEN C S, ANDREASSEN E, JENSEN J S, et al. On the realization of the bulk modulus bounds for two-phase viscoelastic composites[J]. Journal of the Mechanics and Physics of Solids, 2014, 63(1): 228-241.
[10]	HUANG X D, ZHOU S W, SUN G Y, et al. Topology optimization for microstructures of viscoelastic composite materials[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 283: 503-516. doi: 10.1016/j.cma.2014.10.007
[11]	HASHIN Z, SHTRIKMAN S. A variational approach to the theory of the elastic behaviour of multiphase materials[J]. Journal of the Mechanics and Physics of Solids, 1963, 11(2): 127-140. doi: 10.1016/0022-5096(63)90060-7
[12]	HASHIN Z. Complex moduli of viscoelastic composites, Ⅰ: general theory and application to particulate composites[J]. International Journal of Solids and Structures, 1970, 6(5): 539-552. doi: 10.1016/0020-7683(70)90029-6
[13]	杨大鹏, 刘新田. 复合材料有效弹性模量的上、下限的求解[J]. 郑州大学学报(工学版), 2002, 23(2): 106-109. (YANG Dapeng, LIU Xintian. Solution to the upper and lower bounds of the effective elastic modulus of composite materials[J]. Journal of Zhengzhou University (Engineering Edition), 2002, 23(2): 106-109.(in Chinese) YANG Dapeng, LIU Xintian. Solution to the upper and lower bounds of the effective elastic modulus of composite materials[J]. Journal of Zhengzhou University (Engineering Edition), 2002, 23(2): 106-109. (in Chinese))
[14]	LIU Q M, RUAN D, HUANG X. Topology optimization of viscoelastic materials on damping and frequency of macrostructures[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 337: 305-323. doi: 10.1016/j.cma.2018.03.044
[15]	程可朋, 王宪杰, 张洵安, 等. 周期性复合材料构型及结构一体化优化[J]. 应用数学和力学, 2015, 36(7): 725-732. (CHENG Kepeng, WANG Xianjie, ZHANG Xun’an, et al. Collaborative optimization of structures with periodic composite materials[J]. Applied Mathematics and Mechanics, 2015, 36(7): 725-732.(in Chinese) doi: 10.3879/j.issn.1000-0887.2015.07.005 CHENG Kepeng, WANG Xianjie, ZHANG Xunan, et al. Collaborative optimization of structures with periodic composite materials[J]. Applied Mathematics and Mechanics, 2015, 36(7): 725-732. (in Chinese)) doi: 10.3879/j.issn.1000-0887.2015.07.005
[16]	SIGMUND O. Materials with prescribed constitutive parameters: an inverse homogenization problem[J]. International Journal of Solids and Structures, 1994, 31(17): 2313-2329. doi: 10.1016/0020-7683(94)90154-6
[17]	XIA L, BREITKOPF P. Design of materials using topology optimization and energy-based homogenization approach in Matlab[J]. Structural and Multidisciplinary Optimization, 2015, 52(6): 1229-1241. doi: 10.1007/s00158-015-1294-0
[18]	GAO J, LI H, GAO L, et al. Topological shape optimization of 3D micro-structured materials using energy-based homogenization method[J]. Advances in Engineering Software, 2018, 116: 89-102. doi: 10.1016/j.advengsoft.2017.12.002
[19]	SIGMUND O. Morphology-based black and white filters for topology optimization[J]. Structural and Multidisciplinary Optimization, 2007, 33(4): 401-424.
[20]	ZHANG D D, WU Y H, LU X, et al. Topology optimization of constrained layer damping plates with frequency- and temperature-dependent viscoelastic core via parametric level set method[J]. Mechanics of Advanced Materials and Structures, 2021, 29(1): 154-170.