双移动机械臂空间协作动力学建模研究

董方方; 喻斌; 赵晓敏; 陈珊

doi:10.21656/1000-0887.420223

双移动机械臂空间协作动力学建模研究

doi: 10.21656/1000-0887.420223

董方方^{1, 2},
喻斌¹,
赵晓敏^3, ,,
陈珊¹

1.
合肥工业大学机械工程学院，合肥 230009
2.
安徽省智能数控技术及装备工程实验室，合肥 230009
3.
合肥工业大学汽车与交通工程学院，合肥 230009

基金项目: 国家自然科学基金(51905140)；安徽省自然科学基金(2208085ME126)

详细信息

作者简介:
董方方（1988— ），男，副教授，硕士生导师（E-mail：fangfangdong@hfut.edu.cn）

赵晓敏（1986— ），女，副教授，硕士生导师（通讯作者. E-mail：zhaoxiaomin@hfut.edu.cn）

中图分类号: O313.3
计量
- 文章访问数: 591
- HTML全文浏览量: 264
- PDF下载量: 52
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-02
- 修回日期: 2021-11-02
- 网络出版日期: 2022-07-05
- 刊出日期: 2022-08-01

Dynamic Modeling of Spatial Cooperation Between Dual-Arm Mobile Manipulators

DONG Fangfang^{1, 2},
YU Bin¹,
ZHAO Xiaomin^{3
, ,},
CHEN Shan¹

1.
School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, P.R.China
2.
Anhui Engineering Laboratory of Intelligent CNC Technology and Equipment, Hefei 230009, P.R.China
3.
School of Automotive and Transportation Engineering, Hefei University of Technology, Hefei 230009, P.R.China

摘要

摘要:
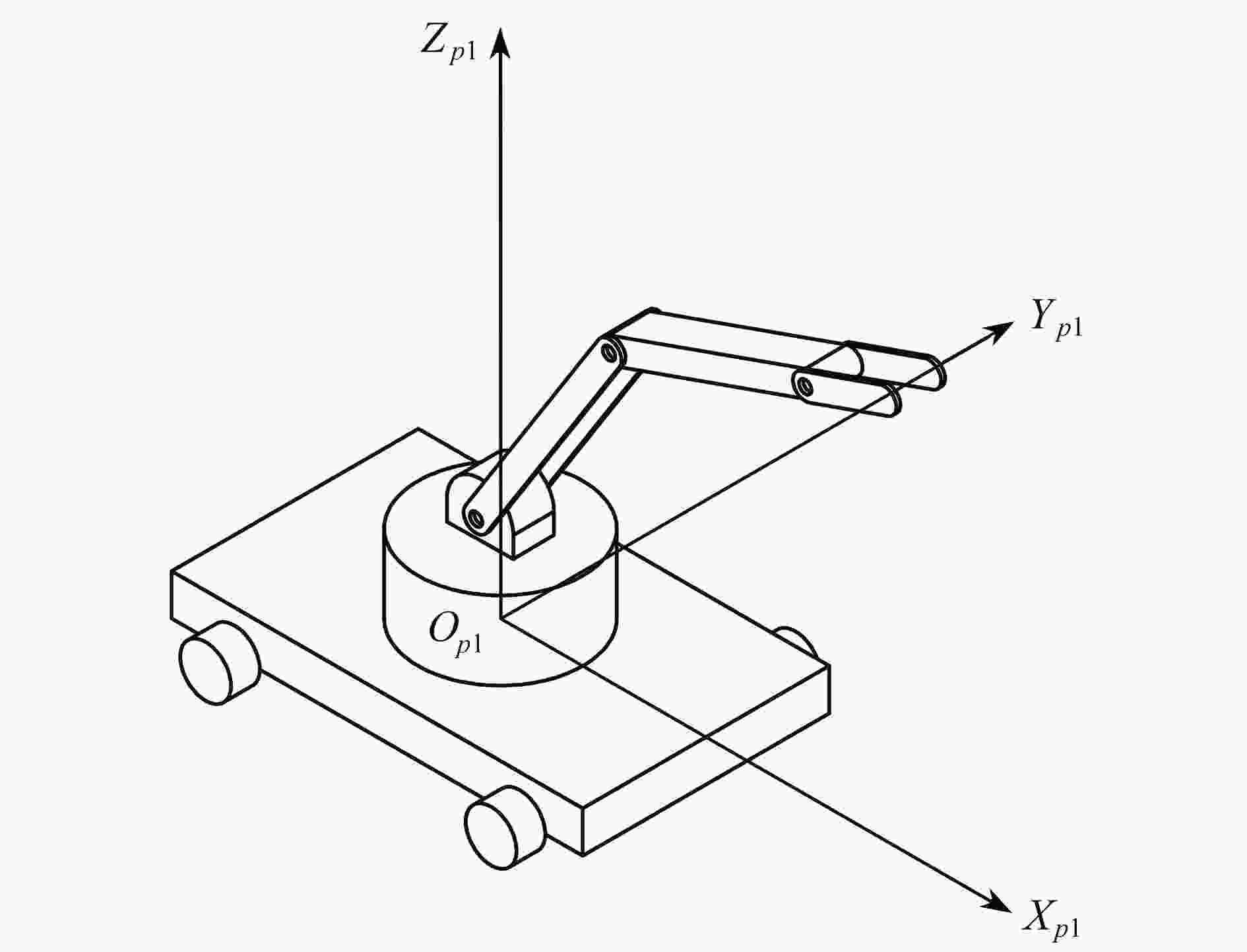
移动机械臂进行空间协作时会产生复杂的非线性耦合，使得采用Lagrange方程或Newton-Euler法直接进行建模极为繁琐。针对双移动机械臂空间协作问题，提出了一种结合Udwadia-Kalaba (U-K)方法与Lagrange方程建立动力学模型的方法。在建模过程中，将负载简化为连杆，选择负载中心断开的方式对系统进行分解，从而避免了机械臂末端关节断开导致的末端关节转角与连杆转角的约束信息缺失问题；将分割形成的两个子系统通过Lagrange方程进行建模，得到了子系统的动力学模型；再将协作系统的固有几何关系通过约束形式引入，应用U-K方法得到了协作系统动力学模型，减少了建立动力学模型所需要的计算量；最后通过数值仿真验证了该方法所得到的动力学模型的准确性。
- Udwadia-Kalaba方法 /
- 动力学建模 /
- 协作机械臂 /
- 移动机械臂
Abstract:
The complex nonlinear coupling in the spatial cooperation process of mobile manipulators, makes it extremely tedious to directly model the spatial cooperative systems with the Lagrange equation or the Newton-Euler method. A dynamic modeling method, combining the Udwadia-Kalaba (U-K) method with the Lagrange equation, was proposed for spatial cooperation of dual-arm mobile manipulators. The load was simplified as a connecting link during modeling. The load center was selected to be disconnected for decomposition, so that the lack of constraint information was avoided between the end joint angle and the end link angle caused by the disconnection of the manipulator end joint; the segmented 2 subsystems were modeled with the Lagrange equation, thus, the dynamic model for the subsystems was obtained. The inherent geometric relationships of the cooperative system were introduced in the form of constraints, and the U-K method was applied to obtain the dynamic model for the cooperative system. The computation for modeling was reduced. The numerical simulation verifies the accuracy of the model.
- Udwadia-Kalaba method /
- dynamic modeling /
- cooperative manipulator /
- mobile manipulator

HTML全文

图 1 移动机械臂示意图

Figure 1. The schematic of the mobile manipulator

下载: 全尺寸图片幻灯片

图 2 双移动机械臂空间协作系统示意图： (a) 主视图；(b) 俯视图

Figure 2. The schematic of dual-system cooperative handling mobile manipulators: (a) the main view; (b) the vertical view

下载: 全尺寸图片幻灯片

图 3 断开处轨迹示意图

Figure 3. Trajectories at disconnection points

下载: 全尺寸图片幻灯片

图 5 移动平台位移示意图

Figure 5. Displacements of mobile platforms

下载: 全尺寸图片幻灯片

图 4 关节角度约束示意图

Figure 4. Joint angle constraints

下载: 全尺寸图片幻灯片

图 6 子系统转角示意图：(a) 左半子系统；(b)右半子系统

Figure 6. Rotation angles of subsystems: (a) the left subsystem; (b) the right subsystem

下载: 全尺寸图片幻灯片

表 1 系统动力学参数表

Table 1. Dynamic parameters of system

object	mass $ m / \mathrm{k}\mathrm{g}$	moment of inertia $I / (\mathrm{k}\mathrm{g}\cdot {\mathrm{m} }^{2})$	length $ l / \mathrm{m} $
mobile platform $ {v}_{1} $	$ 50 $	$ 0 $	$ 0 $
joint $ {r}_{1} $	$ 2 $	$0.062\;5$	$ 0.5 $
link $ 1 $	$ 3 $	$0.490\;0$	$ 0.7 $
link $ 2 $	$ 4 $	$0.855\;0$	$ 0.8 $
link $ 3 $	$ 1 $	$0.080\;0$	$ 0.4 $
mobile platform $ {v}_{2} $	$ 50 $	$ 0 $	$ 0 $
joint $ {r}_{2} $	$ 2 $	$0.062\;5$	$ 0.5 $
link $ 4 $	$ 3 $	$0.490\;0$	$ 0.7 $
link $ 5 $	$ 4 $	$0.855\;0$	$ 0.8 $
link $ 6 $	$ 1 $	$0.080\;0$	$ 0.4 $

下载: 导出CSV

参考文献(25)

[1]	TSUJI T, JAZIDIE A, KANEKO M. Distributed trajectory generation for cooperative multi-arm robots via virtual force interactions[J]. IEEE Transactions on Systems, Man, and Cybernetics (Part B): Cybernetics, 1997, 27(5): 862-867. doi: 10.1109/3477.623238
[2]	YAN Z, JOUANDEAU N, CHERIF A A. A survey and analysis of multi-robot coordination[J]. International Journal of Advanced Robotic Systems, 2013, 10(12): 283-290.
[3]	沈显庆, 孙启智, 马志鹏. 基于双闭环P+前馈的移动机器人路径跟随控制[J]. 黑龙江科技大学学报, 2021, 31(2): 223-228 doi: 10.3969/j.issn.2095-7262.2021.02.015 SHEN Xianqing, SUN Qizhi, MA Zhipeng. Path following control of mobile robot based on double closed loop P+ with feedforward compensation[J]. Journal of Heilongjiang University of Science and Technology, 2021, 31(2): 223-228.(in Chinese) doi: 10.3969/j.issn.2095-7262.2021.02.015
[4]	郭隆臻, 徐定明, 李子信. 移动送料机器人地图构建与运动控制研究[J]. 智能计算机与应用, 2021, 11(1): 55-60 doi: 10.3969/j.issn.2095-2163.2021.01.013 GUO Longzhen, XU Dingming, LI Zixin. Research on map construction and motion control of mobile feeding robot[J]. Intelligent Computer and Applications, 2021, 11(1): 55-60.(in Chinese) doi: 10.3969/j.issn.2095-2163.2021.01.013
[5]	杨秀清. 机电液耦合的搬运机械手虚拟样机研究[D]. 博士学位论文. 合肥: 中国科学技术大学, 2008. YANG Xiuqing. Research on virtual prototyping of mechanical-electrical-hydraulic coupling manipulator[D]. PhD Thesis. Hefei: University of Science and Technology of China, 2008. (in Chinese)
[6]	姜峣, 李铁民, 王立平. 过约束并联机构动力学建模方法[J]. 机械工程学报, 2013, 49(17): 123-129 doi: 10.3901/JME.2013.17.123 JIANG Yao, LI Tiemin, WANG Liping. Research on the dynamic model of an over-constrained parallel mechanism[J]. Journal of Mechanical Engineering, 2013, 49(17): 123-129.(in Chinese) doi: 10.3901/JME.2013.17.123
[7]	刘铖, 胡海岩. 基于李群局部标架的多柔体系统动力学建模与计算[J]. 力学学报, 2021, 53(1): 213-233 LIU Cheng, HU Haiyan. Dynamic modeling and computation for flexible multibody systems based on the local frame of Lie group[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(1): 213-233.(in Chinese)
[8]	陈俊斌. 双柔性机械臂多刚体模拟方法研究[D]. 硕士学位论文. 福州: 福州大学, 2006. CHEN Junbin. Using multirigid-body method for the simulation of two flexible manipulators[D]. Master Thesis. Fuzhou: Fuzhou University, 2006. (in Chinese)
[9]	JORGE G L, ARTEAGA M A. Dynamic model and simulation of cooperative robots: a case study[J]. Robotica, 2005, 23(5): 615-624. doi: 10.1017/S0263574704001213
[10]	PARRA-VEGA V, RODRÍGUEZ-ANGELES A, ARIMOTO S, et al. High precision constrained grasping with cooperative adaptive handcontrol[J]. Journal of Intelligent & Robotic Systems, 2001, 32(3): 235-254.
[11]	FLIXEDER S, T GLÜCK, KUGI A. Force-based cooperative handling and lay-up of deformable materials: mechatronic design, modeling, and control of a demonstrator[J]. Mechatronics, 2017, 47: 246-261. doi: 10.1016/j.mechatronics.2016.10.003
[12]	章定国. 多杆空间柔性机器人递推Lagrange动力学建模和仿真[J]. 应用数学和力学, 2009, 30(10): 1202-1212 doi: 10.3879/j.issn.1000-0887.2009.10.008 ZHANG Dingguo. Recursive Lagrangian dynamic modeling and simulation of multi-link spatial flexible manipulator arms[J]. Applied Mathematics and Mechanics, 2009, 30(10): 1202-1212.(in Chinese) doi: 10.3879/j.issn.1000-0887.2009.10.008
[13]	郭益深, 陈力. 双臂空间机器人姿态、关节协调运动基于RBF神经网络的自适应控制算法[J]. 应用数学和力学, 2008, 29(9): 1028-1036 doi: 10.3879/j.issn.1000-0887.2008.09.003 GUO Yishen, CHEN Li. Adaptive neural network control for coordinated motion of dual-arm space robot system with uncertain parameters[J]. Applied Mathematics and Mechanics, 2008, 29(9): 1028-1036.(in Chinese) doi: 10.3879/j.issn.1000-0887.2008.09.003
[14]	REZA M, S. MEHDI R, ALI T. A new observer-based adaptive controller for cooperative handling of an unknown object[J]. Robotica, 2014, 34(7): 1437-1463.
[15]	UDWADIA F E, KALABA R E. A new perspective on constrained motion[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1992, 439(1906): 407-410.
[16]	UDWADIA F E. A new perspective on tracking control of nonlinear structural and mechanical systems[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2003, 459(2035): 1783-1800. doi: 10.1098/rspa.2002.1062
[17]	韩江, 汪鹏, 董方方, 等. 基于Udwadia-Kalaba方法的平面冗余并联机器人建模与轨迹跟踪控制[J]. 应用数学和力学, 2020, 41(11): 1183-1196 HAN Jiang, WANG Peng, DONG Fangfang, et al. Modeling and control of planar redundant parallel robots based on the Udwadia-Kalaba method[J]. Applied Mathematics and Mechanics, 2020, 41(11): 1183-1196.(in Chinese)
[18]	HUANG J, CHEN Y H, ZHIHUA Z. Udwadia-Kalaba approach for parallel manipulator dynamics[J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 135(6): 061003-061014. doi: 10.1115/1.4024600
[19]	韩江, 王凡志, 董方方, 等. 基于Udwadia-Kalaba理论的协作机器人轨迹跟踪控制[J]. 组合机床与自动化加工技术, 2021(1): 78-83 HAN Jiang, WANG Fanzhi, DONG Fangfang, et al. A novel trajectory tracking control of collaborative robot based on Udwadia-Kalaba theory[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2021(1): 78-83.(in Chinese)
[20]	刘佳, 刘荣. 双臂协调机械手动力学建模的新方法[J]. 北京航空航天大学学报, 2016, 42(9): 1903-1910 doi: 10.13700/j.bh.1001-5965.2015.0555 LIU Jia, LIU Rong. New approach for dynamics modeling of dual-arm cooperating manipulators[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(9): 1903-1910.(in Chinese) doi: 10.13700/j.bh.1001-5965.2015.0555
[21]	ZHEN S. Study on Lyapunov-based deterministic robust control (LDRC) of uncertain mechanical systems[D]. PhD Thesis. Hefei: Hefei University of Technology, 2014.
[22]	UDWADIA F E, KALABA R E. Analytical Dynamics: a New Approach[M]. Cambridge: Cambridge University Press, 1996.
[23]	CHEN Y H, LEITMANN G, CHEN J S. Robust control for rigid serial manipulators: a general setting[C]// IEEE American Control Conference (ACC). 1998, 2: 912-916.
[24]	SPONG M W, HUTCHINSON S, VIDYASAGAR M. Robot Modeling and Control[M]. New Jersey: John Wiley & Sons Inc, 2006.
[25]	SLOTINE J J, LI W. Applied Nonlinear Control[M]. New Jersey: Prentice Hall, 1991.