New Exact Solutions to a Class of Fractional-Order Modified Unstable Schrödinger Equations
-
摘要:
研究了分数阶修正的不稳定Schrödinger方程(FMUSE)，该方程描述了光脉冲在非均匀光纤系统中传播的色散、非线性、增益或吸收变化的普适问题。首先适当地利用广义分数波变换将FMUSE转化为常微分方程，分离实部和虚部并分别令为零，得到了色散关系。再利用修改的(G'/G)-展开法，求得了一系列带参数的新精确解析解，其中包括三角函数解、双曲函数解和有理函数解，并给出了保证解存在的约束条件。最后当参数取特殊值时得到暗孤波和周期波解。
-
关键词:
- 修改的(G'/G)-展开法 /
- 分数阶修正的不稳定Schrödinger方程 /
- 精确解
Abstract:The fractional-order modified unstable Schrödinger equation (FMUSE) was studied, which describes the dispersion, nonlinearity, gain or absorption variation of optical pulses propagating in nonuniform fiber systems. First, the generalized fractional wave transform was appropriately used to convert the FMUSE into an ordinary differential equation, and the real and imaginary parts were separated and set as zero respectively, and the dispersion relation was obtained. By means of the modified (G'/G)-expansion method, a series of new exact analytical solutions with parameters were obtained, including trigonometric solutions, hyperbolic solutions and rational solutions, and the constraints ensuring the existence of solutions were given. Finally, the solutions of the dark solitary wave and the periodic wave were obtained with the parameters of special values.
-
图 1
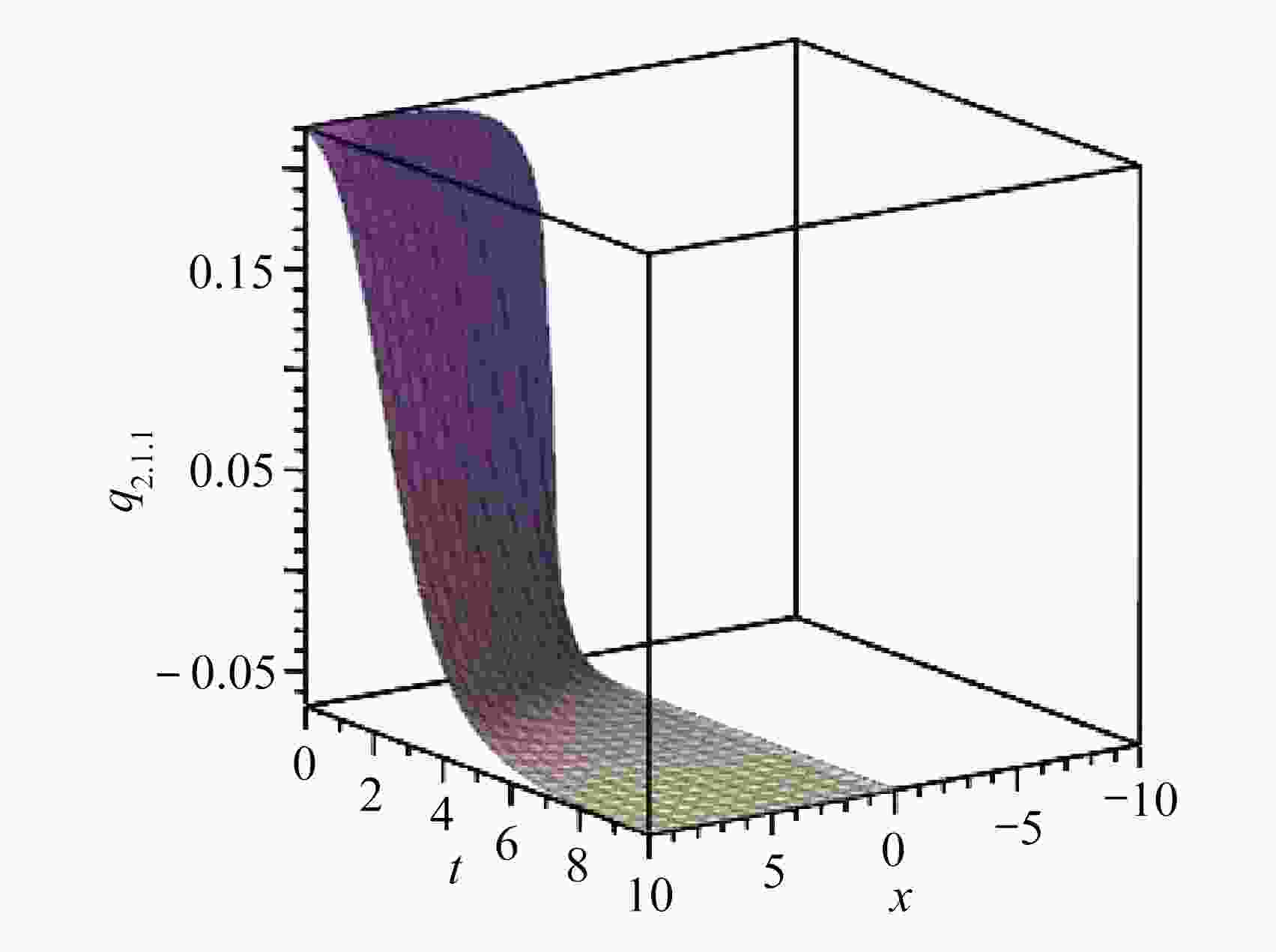
$ \lambda = 3,{\kern 1pt} \mu = 2,{\kern 1pt} K = 1,{\kern 1pt} {\kern 1pt} v = 1,{\kern 1pt} {\kern 1pt} \beta = - 1,{\kern 1pt} $ $c = 1,{\kern 1pt} {\kern 1pt} s = - 15,{\kern 1pt} {\kern 1pt} \alpha = {1}/{2}$ 时，${q}_{2.1.1}$ 的图像Figure 1. The graphic corresponding to
${q}_{2.1.1}$ ($ \lambda = 3,{\kern 1pt} \mu = 2,{\kern 1pt} K = 1,{\kern 1pt} {\kern 1pt} v = 1,{\kern 1pt} {\kern 1pt} \beta = - 1,{\kern 1pt} $ $c = 1,{\kern 1pt} {\kern 1pt} s = - 15,{\kern 1pt} {\kern 1pt} \alpha = {1}/{2}$ )
图 2
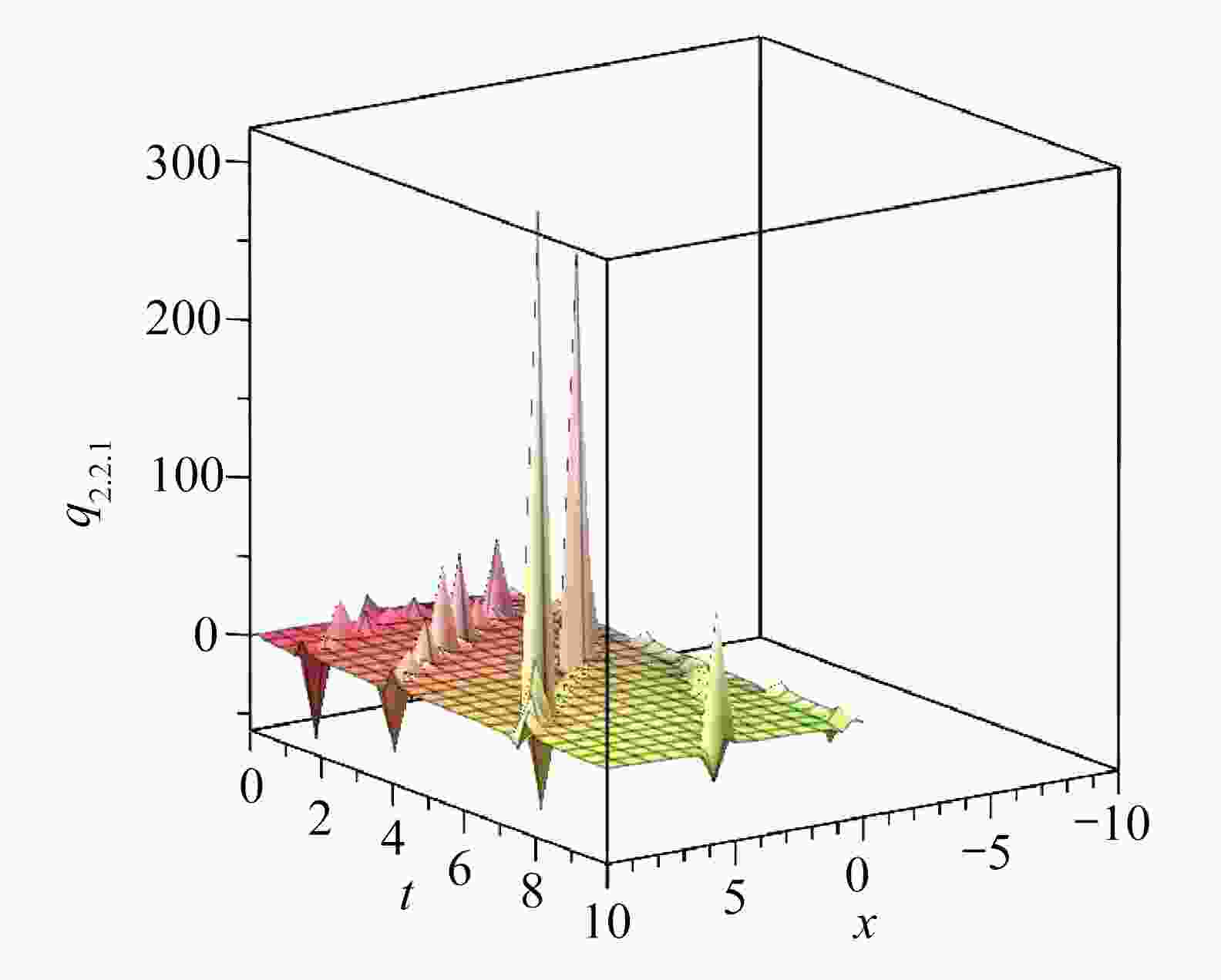
$\lambda = 2,\;\mu = 2,\;K = 1,\;v = 1,\;\beta = - 1,\; c = 1,\;s =-5,\;\alpha = {1}/{2}$ 时，$ {q_{2.2.1}} $ 的图像Figure 2. The graphic corresponding to
$ {q_{2.2.1}} $ ($\lambda = 2,{\kern 1pt} \mu = 2,{\kern 1pt} K = 1, v = 1, $ $ {\kern 1pt} \beta = - 1,{\kern 1pt}$ $c = 1,{\kern 1pt} {\kern 1pt} s = - 5,{\kern 1pt} {\kern 1pt} \alpha = {1}/{2}$ )
图 3
$\lambda = 2,\; \mu = 2, \;K = 1, \; v = 1,\; \beta = - 1,\;c = 1, \; s = - 5, \; \alpha = {1}/{2}$ 时，$ {q_{2.2.2}} $ 的图像Figure 3. The graphic corresponding to
$ {q_{2.2.2}} $ ($\lambda = 2, \mu = 2, K = 1, v = 1, $ $ \beta = - 1,$ $c = 1, s = - 5, \alpha = {1}/{2}$ ) -
[1] ZULFIQAR A, AHMAD J. Soliton solutions of fractional modified unstable Schrödinger equation using exp-function method[J]. Results in Physics, 2020, 19: 103476. doi: 10.1016/j.rinp.2020.103476 [2] MIRZAZADEH M, YILDIRIM Y, YASAR E, et al. Optical solitons and conservation law of Kundu-Eckhaus equation[J]. Optik, 2018, 154: 551-557. doi: 10.1016/j.ijleo.2017.10.084 [3] ZHOU Q, MIRZAZADEH M, ZERRAD E, et al. Bright, dark, and singular solitons in optical fibers with spatio-temporal dispersion and spatially dependent coefficients[J]. Journal of Modern Optics, 2016, 63(10): 950-954. doi: 10.1080/09500340.2015.1111456 [4] KARA A H, RAZBOROVA P, BISWAS A. Solitons and conservation laws of coupled Ostrovsky equation for internal waves[J]. Applied Mathematics and Computation, 2015, 258: 95-99. doi: 10.1016/j.amc.2015.01.093 [5] SEADAWY A R, IQBAL M, LU D. Construction of soliton solutions of the modify unstable nonlinear Schrödinger dynamical equation in fiber optics[J]. Indian Journal of Physics, 2020, 94: 823-832. doi: 10.1007/s12648-019-01532-5 [6] HONG B, LU D, CHEN W. Exact and approximate solutions for the fractional Schrödinger equation with variable coefficients[J]. Advances in Differences Equations, 2019, 2019(1): 370. doi: 10.1186/s13662-019-2313-z [7] DODD R K, EILBECK J C, GIBBON J D, et al. Solitons and Nonlinear Wave Equations[M]. Academic Press Inc, 1982. [8] SAVESCU M, BHRAWY A H, ALSHAERY A A, et al. Optical solitons in nonlinear directional couplers with spatio-temporal dispersion[J]. Journal of Modern Optics, 2014, 61(5): 441-458. doi: 10.1080/09500340.2014.894149 [9] ARSHAD M, SEADAWY A R, LU D. Bright-dark solitary wave solutions of generalized higher-order nonlinear Schrödinger equation and its applications in optics[J]. Journal of Electromagn Waves and Applications, 2017, 31(16): 1711-1121. doi: 10.1080/09205071.2017.1362361 [10] YANG Z J, ZHANG S M, LI X L, et al. Variable sinh-Gaussian solitons in nonlocal nonlinear Schrödinger equation[J]. Applied Mathematics Letters, 2018, 82: 64-70. doi: 10.1016/j.aml.2018.02.018 [11] JIA R R, GUO R. Breather and rogue wave solutions for the (2+1)-dimensional nonlinear Schrödinger-Maxwell-Bloch equation[J]. Applied Mathematics Letters, 2019, 93: 117-123. doi: 10.1016/j.aml.2019.02.001 [12] 江林, 孙峪怀, 张雪, 等.2+1)维时空分数阶Nizhnik-Novikov-Veslov方程的精确行波解及其分支[J]. 应用数学和力学, 2018, 39(11): 1313-1322. (JIANG Lin, SUN Yuhuai, ZHANG Xue, et al. Exact traveling wave solutions and bifurcations of (2+1)-dimensional space-time fractional-order Nizhnik-Novikov-Veslov equations[J]. Applied Mathematics and Mechanics, 2018, 39(11): 1313-1322. (in Chinese) [13] 石兰芳, 聂子文. 应用全新(G'/G)-展开方法求解广义非线性Schrödinger方程和耦合非线性Schrödinger方程组[J]. 应用数学和力学, 2017, 38(5): 539-552SHI Lanfang, NIE Ziwen. Solutions to the nonlinear Schrödinger equation and coupled nonlinear Schrödinger equations with a new (G'/G)-expansion method[J]. Applied Mathematics and Mechanics, 2017, 38(5): 539-552.(in Chinese) [14] ZAYED E, GEPREEL K A. The Modified (G′/G)-Expansion Method and Its Applications to Construct Exact Solutions for Nonlinear PDEs[M]. World Scientific and Engineering Academy and Society (WSEAS), 2011. [15] KUMAR V. Modified (G'/G)-expansion method for finding traveling wave solutions of the coupled Benjamin-Bona-Mahony-KdV equation[J]. Journal of Ocean Engineering and Science, 2019, 4(3): 252-255. doi: 10.1016/j.joes.2019.04.008 [16] JUMARIE G. Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results[J]. Computers and Mathematics With Applications, 2006, 51(9/10): 1367-1376. -
下载:
计量
- 文章访问数: 524
- HTML全文浏览量: 227
- PDF下载量: 101
- 被引次数: 0
渝公网安备50010802005915号