A Green’s Function Construction Method of the Single Well Seepage Model for Asymmetric Fractures
-
摘要:
不对称裂缝渗流规律可借助Green函数方法进行求解。根据基本渗流理论,建立了不对称裂缝点源数学模型,采用无因次化与Laplace变换,得到了Laplace空间的无因次点源数学模型微分方程。将未知Green函数与点源微分方程相结合,并考虑点源微分方程的齐次条件以及点源微分方程的特征,给出了如何构造Green函数使之满足点源微分方程齐次边界以及未知目标函数求解的一般方法。根据空间Green函数的对称性和连续性,得出了不对称裂缝点源模型Green函数的形式。最后通过不对称裂缝压裂直井渗流数学模型,验证了该文给出的Green函数两种形式与文献和商业试井分析软件Saphir的数值计算结果一致。
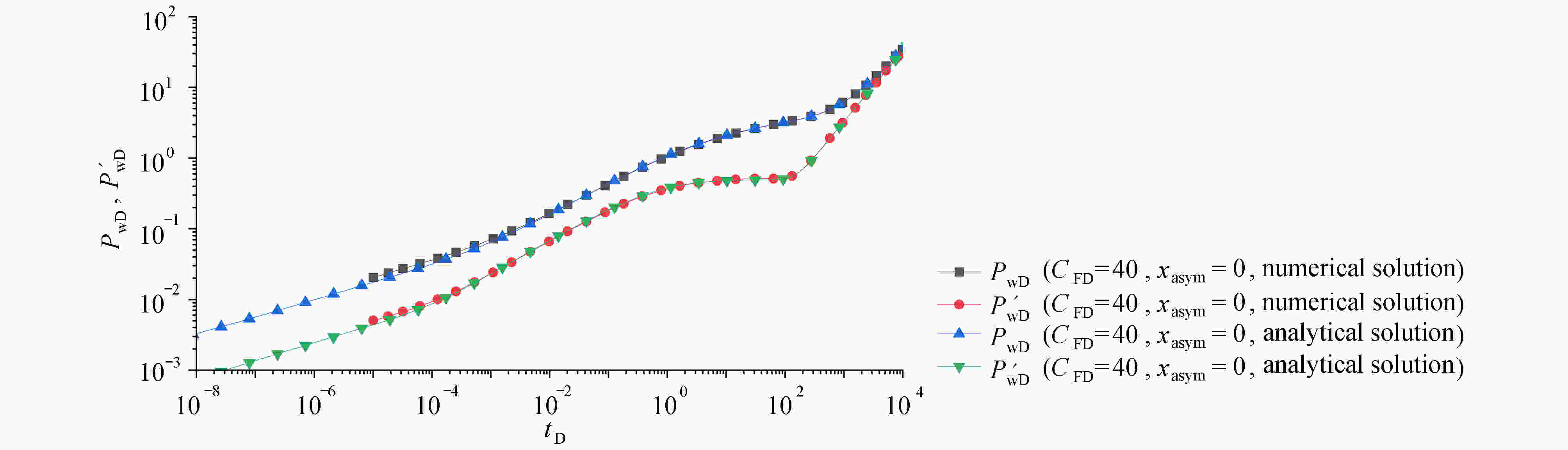
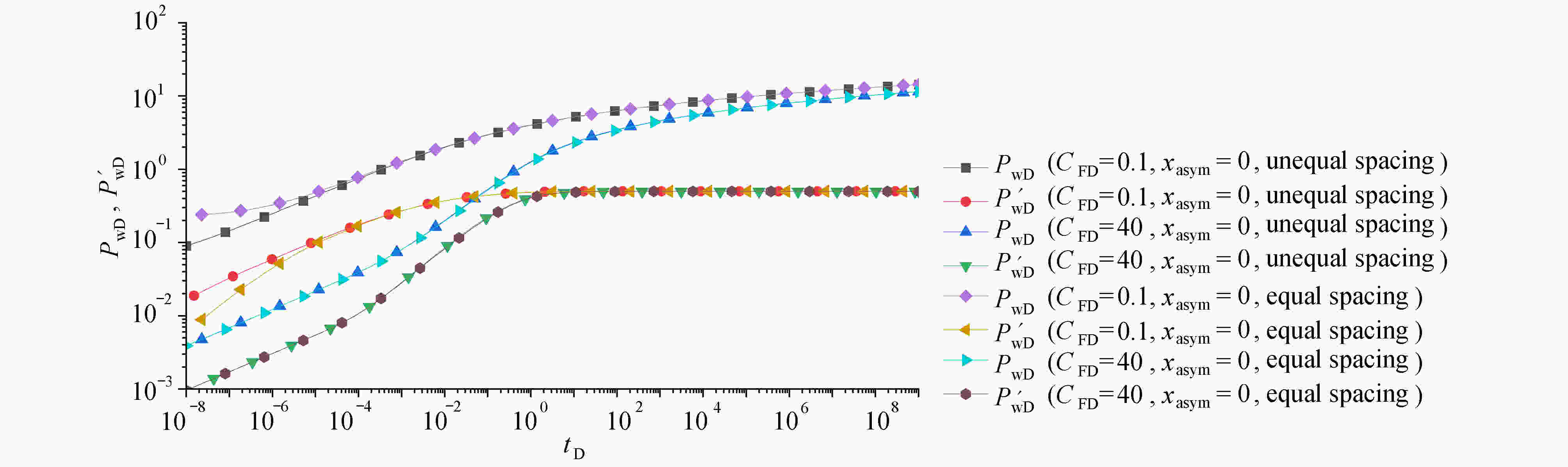
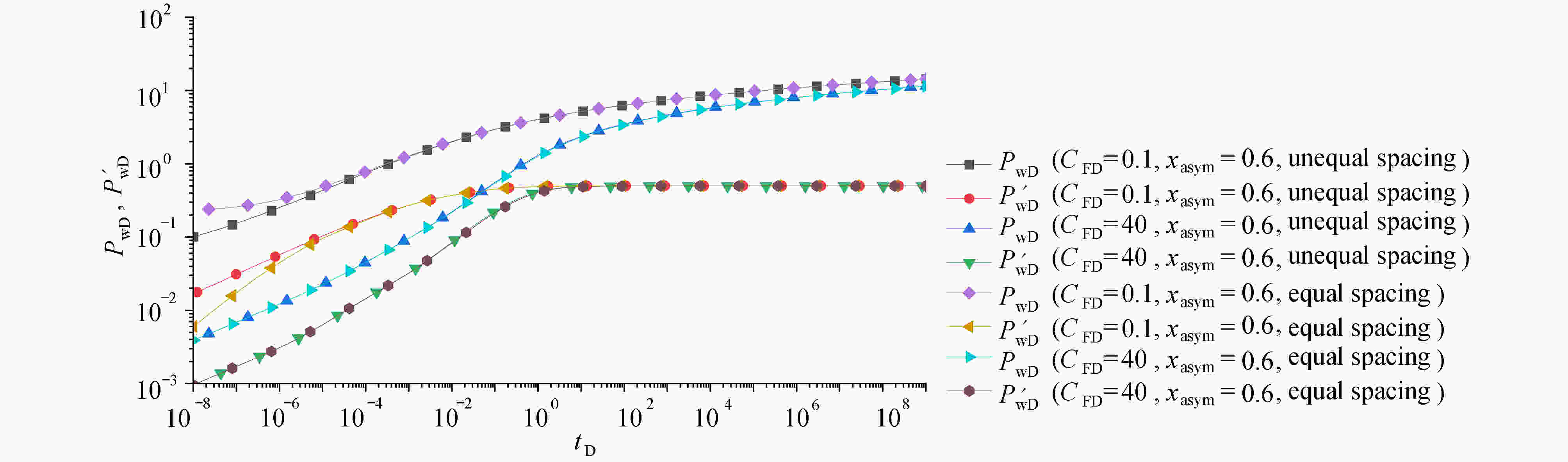
Abstract:The seepage law for asymmetric fractures can be solved by the Green’s function method. According to the basic seepage theory, the point source mathematical model for asymmetric fractures was established. The dimensionless point source mathematical model differential equation in the Laplacian space was obtained through the dimensionless transformation and the Laplacian transformation. By means of the unknown Green’s function combined with the point source differential equation, and in view of the homogeneous boundary conditions for the point source differential equation and the characteristics of the point source differential equation, a general construction method for Green’s function was given to meet the homogeneous boundary conditions for the point source differential equation and the solution of the unknown objective function. According to the symmetry and continuity of spatial Green’s function, the Green form of the asymmetric fracture point source model was obtained. Finally, through the seepage mathematical model for the asymmetric-fracture vertical well, it was verified that the 2 forms of Green’s function are consistent with the results calculated in references and with the commercial well test analysis software Saphir.
-
Key words:
- Green’s function /
- asymmetric fracture /
- fractured well /
- unequal-spacing grid
-
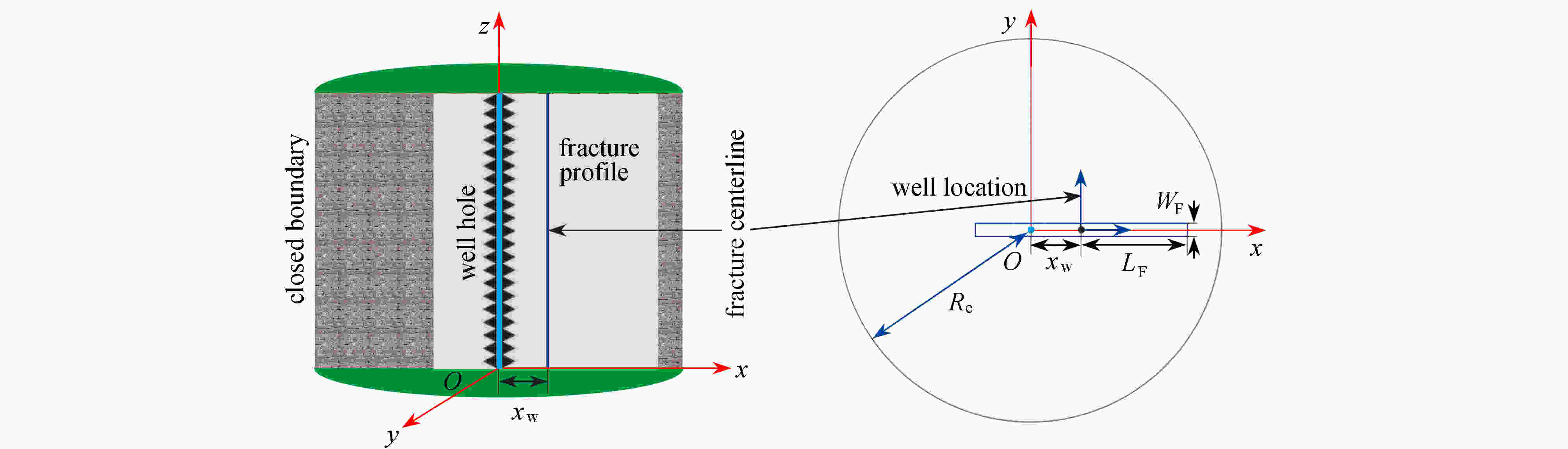
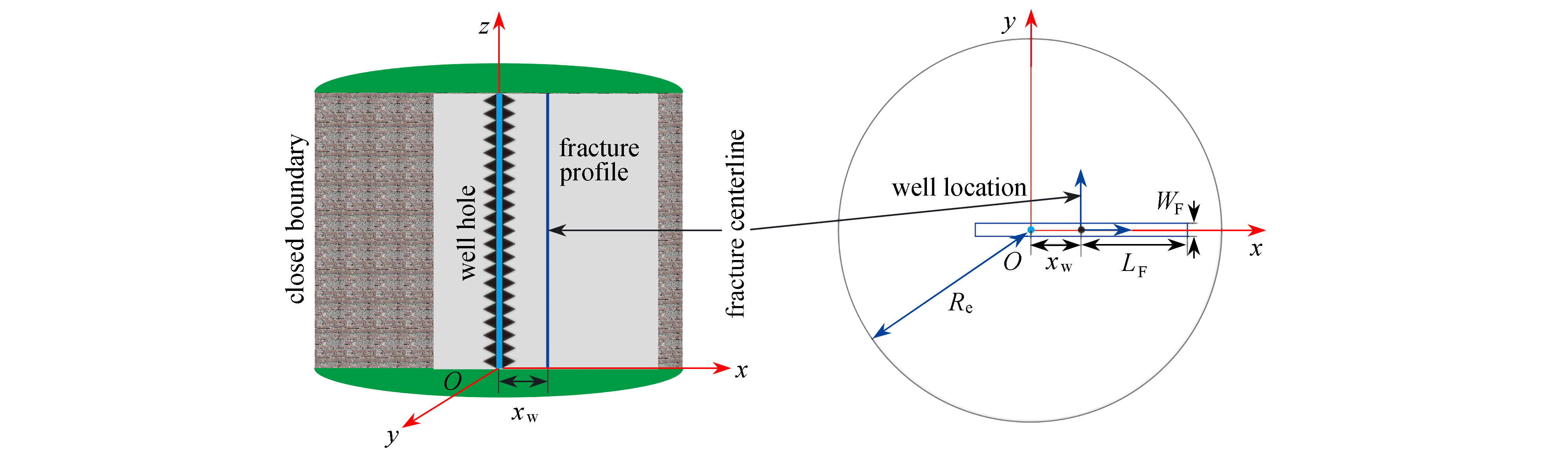
符号说明 $ {x_{\text{w}}} $ 井偏离裂缝中心位置的位移,m $ {L_{\text{F}}} $ 裂缝的半长,m $ {W_{\text{F}}} $ 裂缝的宽度,m $ {k_{\text{F}}} $ 裂缝的渗透率,m2 $ {p_{\text{F}}} $ 裂缝中流体压力,Pa $ \mu $ 流体的黏度,Pa.s $ q $ 1/2裂缝单元总流量,m3/s $ h $ 储层厚度,m $ {L_{{\text{ref}}}} $ 参考长度,一般取裂缝的半长,m ${\text{δ} }\left( {x - {x_{\text{w} } } } \right)$ Dirac函数 $ k $ 储层的有效渗透率,m2 $ G\left( {{x_{\text{D}}};\alpha } \right) $ 空间位置Green函数 $ s $ Laplace变量 $ {G'}\left( {{x_{\text{D}}};\alpha } \right) $ Green函数一阶导数 $ p $ 地层中任意位置的压力,Pa ${G'' }\left( { {x_{\text{D} } };\alpha } \right)$ Green函数二阶导数 $ {x_{{\text{asmy}}}} $ 不对称因子,无因次 $ \eta \left( {{x_{\text{D}}} - \alpha } \right) $ 单位阶跃函数 $ \alpha $ 空间位置Green函数原像位置,m $ {C_{{\text{FD}}}} $ 无因次裂缝导流能力,无因次 $ {q_{\text{F}}} $ 单位长度裂缝线流量,m3/s $ {{\text{K}}_0}\left( x \right) $ 第二类零阶修正Bessel函数 ${p_{\rm{i}}}$ 原始地层压力,Pa $ {{\text{I}}_0}\left( x \right) $ 第一类零阶Bessel函数 $ {r_{{\text{eD}}}} $ 外边界无因次半径,无因次 $ {x_{{\text{midD}}\left( i \right)}} $ 裂缝离散第i个网格的中点 $ {x_{{\text{D}}\left( j \right)}} $ 裂缝离散第j个网格的左边界 $ {x_{{\text{D}}\left( {j + 1} \right)}} $ 裂缝离散第j个网格的右边界 $ {(\cdot)_{\text{D}}} $ 无因次变量 $ \overline{(\cdot)} $ Laplace空间参数 -
[1] JING L, HEDAN S, AO Z, et al. Non-Darcy binomial deliverability equations for partially penetrating vertical gas wells and horizontal gas wells[J]. Journal of Energy Resources Technology, 2011, 133(4): 043101. doi: 10.1115/1.4005240 [2] WANG L, WANG X D, LI J Q, et al. Simulation of pressure transient behavior for asymmetrically finite-conductivity fractured wells in coal reservoirs[J]. Transport in Porous Media, 013, 7(3): 353-372. [3] WANG L, WANG X D, DING X M, et al. Rate decline curves analysis of a vertical fractured well with fracture face damage[J]. Journal of Energy Resources Technology, 2012, 134(3): 032803. doi: 10.1115/1.4006865 [4] GRINGARTEN A C, RAMEY H J, RAGHAVAN R. Applied pressure analysis for fractured wells[J]. Journal of Petroleum Technology, 1975, 27(7): 887-892. doi: 10.2118/5496-PA [5] CINCOLEY H, HEBER, SAMANIEGO V F, DOMINGUEZ A N. Transient pressure behavior for a well with a finite-conductivity vertical fracture[J]. Society of Petroleum Engineers Journal, 1978, 18(4): 253-264. doi: 10.2118/6014-PA [6] CINCOLEY H, FERNANDO SAMANIEGO V F. Transient pressure analysis for fractured wells[J]. Journal of Petroleum Technology, 1981, 33(9): 1749-1766. doi: 10.2118/7490-PA [7] CRAWFORD P B, LANDRUM B L. Effect of unsymmetrical vertical fractures on production capacity[J]. Transactions of the AIME, 1955, 204(1): 251-254. doi: 10.2118/433-G [8] NARASIMHAN T N, PALEN W A. A purely numerical approach for analyzing flow to a well intercepting a vertical fracture: SPE7983[R]. Department of Energy, USA, 1979. [9] BENNETT C O, ROSATO N D, REYNOLDS A C. Influence of fracture heterogeneity and wing length on the response of vertically fractured wells[J]. Society of Petroleum Engineers Journal, 1983, 23(2): 219-230. doi: 10.2118/9886-PA [10] RESURREICAO C, FERNANDO R. Transient rate behavior of finite-conductivity asymmetrically fractured wells producing at constant pressure[C]//SPE Annual Technical Conference and Exhibition. Dallas, Texas, 1991: SPE-22657-MS. [11] BERUMEN S, TIAB D, RODRIGUEZ F. Constant rate solutions for a fractured well with an asymmetric fracture[J]. Journal of Petroleum Science and Engineering, 2000, 25(1/2): 49-58. [12] TIAB D, JING L, NGUYEN H, et al. Evaluation of fracture asymmetry of finite-conductivity fractured wells[J]. Journal of Energy Resources Technology, 2010, 132(1): 36-49. [13] 田建涛, 赵超峰, 张伟, 等. 水力压裂井中监测方法不对称压裂裂缝分析[J]. 石油物探, 2019, 58(4): 563-571. (TIAN Jiantao, ZHAO Chaofeng, ZHANG Wei, et al. Analysis of asymmetric hydraulic fracture for borehole microseismic monitoring[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 563-571.(in Chinese) doi: 10.3969/j.issn.1000-1441.2019.04.011 [14] 万义钊, 刘曰武, 吴能友, 等. 基于离散裂缝的多段压裂水平井数值试井模型及应用[J]. 力学学报, 2018, 50(1): 147-156. (WAN Yizhao, LIU Yuewu, WU Nengyou, et al. A numerical well test model for multi-fractured horizontal wells based on discrete-fracture model and its application[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(1): 147-156.(in Chinese) doi: 10.6052/0459-1879-17-319 [15] CHEN Z M, LIAO X W, HUANG C H, et al. Productivity estimations for vertically fractured wells with asymmetrical multiple fractures[J]. Journal of Natural Gas Science & Engineering, 2014, 21: 1048-1060. [16] WANG L, WANG X D. Type curves analysis for asymmetrically fractured wells[J]. Journal of Energy Resources Technology, 2014, 136(1): 203101-203108. [17] 王镜惠, 梅明华, 梁正中, 等. 水平井多段压裂非常规裂缝压力动态特征[J]. 新疆石油地质, 2018, 50(1): 147-156. (WANG Jinghui, MEI Minghua, LIANG Zhengzhong, et al. Dynamic pressure characteristics of unconventional fractures during multi-staged fracturing in horizontal wells[J]. Xinjiang Petroleum Geology, 2018, 50(1): 147-156.(in Chinese) [18] 姬安召, 王玉风, 张光生. 不对称垂直裂缝压力动态特征[J]. 计算物理, 2019, 36(1): 47-53. (JI Anzhao, WANG Yufeng, ZHANG Guangsheng. Dynamic pressure characteristics of unconventional fractures during multi-staged fracturing in horizontal wells[J]. Chinese Journal of Computational Physics, 2019, 36(1): 47-53.(in Chinese) [19] MENG M L, CHEN Z M, LIAO X W, et al. A well-testing method for parameter evaluation of multiple fractured horizontal wells with non-uniform fractures in shale oil reservoirs[J]. Advances in Geo-Energy Research, 2020, 4(2): 187-198. doi: 10.26804/ager.2020.02.07 [20] 徐有杰. 水力压裂井复杂裂缝试井模型研究[D]. 硕士学位论文. 成都: 西南石油大学, 2019.XU Youjie. Study on well test model of hydraulic fractured well considering complex fractures[D]. Master Thesis. Chengdu: Southwest Petroleum University, 2019. (in Chinese) [21] OZKAN E, RAGHAVAN R. New solutions for well-test-analysis problems, part 1: analytical considerations[J]. Society of Petroleum Engineers Formation Evaluation, 1991, 6(3): 359-368. [22] OZKAN E, RAGHAVAN R. New solutions for well-test-analysis problems, part 2: computional considerations[J]. Society of Petroleum Engineers Formation Evaluation, 1992, 29(3): 160-175. -




 下载:
下载:

 渝公网安备50010802005915号
渝公网安备50010802005915号