Study of the Optimal Integrated Control of a Dengue Transmission Model
-
摘要:
建立了一个登革热在蚊子和人之间传播的模型，引入了Wolbachia、自我保护和杀虫剂三种控制措施，分别从常数控制和时变控制两个方面进行探讨。首先，分析了常数控制对模型基本再生数的影响，研究发现：Wolbachia有助于减小基本再生数，且基本再生数与自我保护和杀虫剂呈负相关。其次，以使得感染数最少且实施成本最低为目标，使用Pontryagin极值原理讨论最优控制。最后，通过数值模拟展示了最优控制的效果。
Abstract:A transmission model for dengue fever between mosquitoes and human beings was established. Three control measures: Wolbachia, self-protection and insecticide were introduced. The constant control and the time-varying control were discussed respectively. Firstly, the influences of the constant control on the basic regeneration number of the model were analyzed. It is shown that Wolbachia helps reduce the basic regeneration number, and the basic regeneration number is negatively correlated with self-protection and insecticide. Secondly, in order to minimize the number of infections and the implementation cost, the optimal control was discussed with Pontryagin’s extreme value principle. Finally, the effects of the optimal control was demonstrated through numerical simulation.
-
Key words:
- dengue /
- transmission model /
- optimal control /
- numerical simulation
-
图 1 常数控制对登革热感染人数的影响
Figure 1. Effects of constant control on the number of dengue infections
图 2 控制策略对登革热感染人数的影响
Figure 2. Effects of the control strategy on the number of dengue infections
图 3 最优综合控制与单一控制的比较：(a) 两种控制策略下
$u_{1}$ 的变化图；(b) 两种控制策略下$u_{2}$ 的变化图Figure 3. Comparison between the optimal integrated control and the single control: (a) the variation diagram of
$u_{1}$ under 2 control strategies; (b) the variation diagram of$u_{2}$ under 2 control strategies
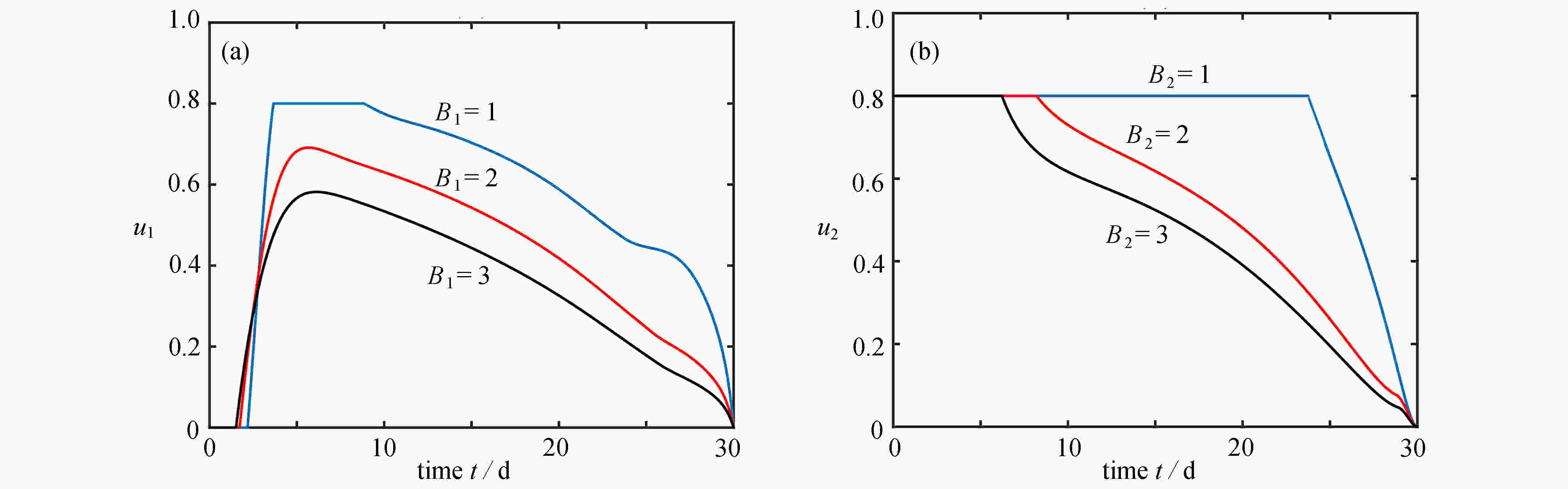
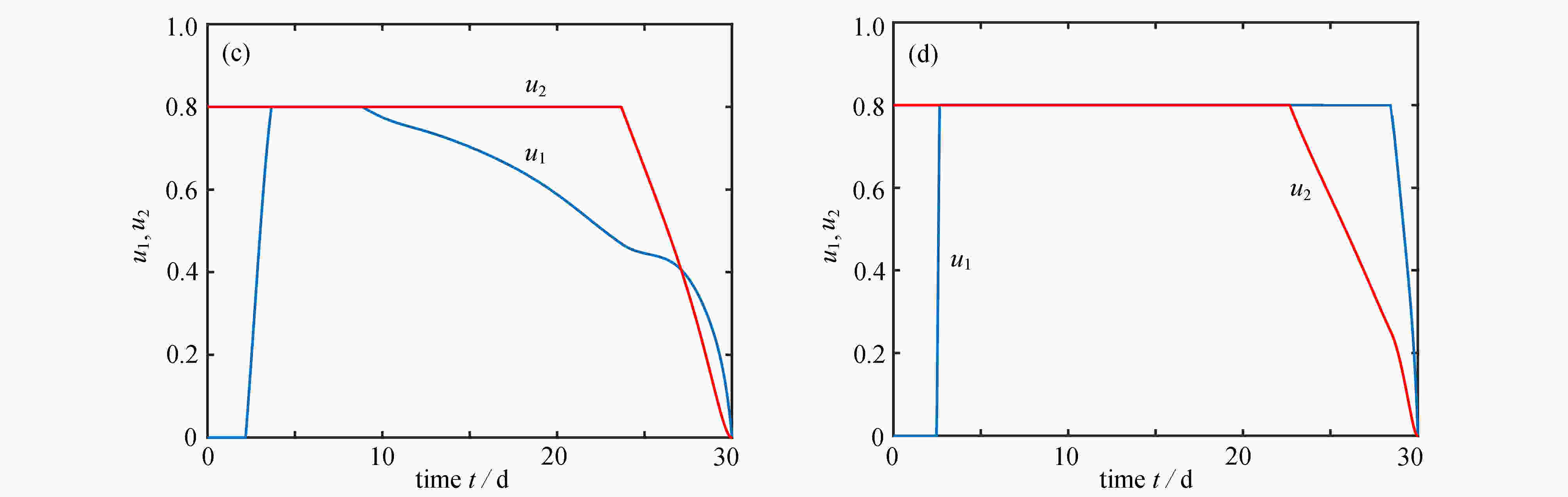
4 不同权重对控制变量的影响：(a) 改变
$B_{1}$ 对$u_1$ 的影响，$A=1, B_{2}=1$ ；(b) 改变$B_{2}$ 对$u_2$ 的影响，$A=1, B_{1}=1$ ；(c) A=1时，$u_{1}, u_{2}$ 的变化图，$B_{1}=1, B_{2}=1$ ；(d)$A=5$ 时，$u_{1}, u_{2}$ 的变化图，$B_{1}=1, B_{2}=1$ 4. The influences of different weights on control variables: (a) the influence of
$B_{1}$ on$u_{1}$ ,$A=1, B_{2}=1$ ; (b) the influence of$B_{2}$ on$u_{2}$ ,$A=1, B_{1}=1$ ; (c) the variation diagram of$u_{1}\; {\rm{and}} \;u_{2},$ $A=1, B_{1}=1, B_{2}=1$ ; (d) the variation diagram of$u_{1}\; {\rm{and}} \;u_{2},$ $A=5$ ,$B_{1}=1, B_{2}=1$ 表 1 模型(1)中各状态变量的含义
Table 1. The meanings of variables in model (1)
state variable biological meaning $S_{{\rm{mi}}}$ mosquito population infected with W and susceptible to D $S_{{\rm{mu}}}$ mosquito population not infected with W and susceptible to D $E_{{\rm{mi}}}$ mosquito population infected with W and in the incubation period of D $E_{{\rm{mu}}}$ mosquito population not infected with W and in the incubation period of D $I_{{\rm{mi}}}$ mosquito population infected with W and D $I_{{\rm{mu}}}$ mosquito population not infected with W but infected with D $S_{{\rm{h}}}$ human population susceptible to D $I_{{\rm{h}}}$ human population infected with D 
下载: 导出CSV
表 2 模型(1)中各参数的含义
Table 2. The meanings of parameters in model (1)
parameter biological meanings $w$ recruitment rate of human beings $b_{{\rm{m}}}$ birth rate of mosquitoes $d_{{\rm{h}}}$ natural death rate of human beings $d_{{\rm{m}}}$ natural death rate of mosquitoes $\beta_{{\rm{h}}}$ D infection rate of human beings bitten by W-free mosquitoes $e_{{\rm{m}}}$ rate at which exposed mosquitoes become infectious $\overline{\beta}_{{\rm{h}}}=q\beta_{{\rm{h}}}$ D infection rate of human beings bitten by W-infected mosquitoes (q<1, which reflects the inhibition effect of W) $\beta_{{\rm{m}}}$ D infection rate of mosquitoes biting D-infected human beings $\gamma_{{\rm{h}}}$ recovery rate of infectious human beings
下载: 导出CSV
-
[1] World Health Organization. Dengue and severe dengue: treatment[EB/OL]. [2021-09-15]. https://www.who.int/health-topics/dengue-and-severe-dengue#tab=tab_3. [2] World Health Organization. Dengue and severe dengue: symptoms[EB/OL]. [2021-09-15]. https://www.who.int/health-topics/dengue-and-severe-dengue#tab=tab_2. [3] AGUSTO F B, KHAN M A. Optimal control strategies for dengue transmission in Pakistan[J]. Mathematical Biosciences, 2018, 305: 102-121. doi: 10.1016/j.mbs.2018.09.007 [4] PRASETYO T A, SARAGIH R, HANDAYANI D. Optimal control on the mathematical models of dengue epidemic by giving vaccination and repellent strategies[J]. Journal of Physics: Conference Series, 2020, 1490(1): 012034. [5] XUE L, REN X, MAGPANTAY F, et al. Optimal control of mitigation strategies for dengue virus transmission[J]. Bulletin of Mathematical Biology, 2021, 83(2): 8. doi: 10.1007/s11538-020-00839-3 [6] FISTER K R, MCCARTHY M L, OPPENHEIMER S F, et al. Optimal control of insects through sterile insect release and habitat modification[J]. Mathematical Biosciences: an International Journal, 2013, 244(2): 201-212. doi: 10.1016/j.mbs.2013.05.008 [7] MASUD M A, KIM B N, KIM Y. Optimal control problems of mosquito-borne disease subject to changes in feeding behavior of Aedes mosquitoes[J]. Biosystems, 2017, 156/157: 23-39. doi: 10.1016/j.biosystems.2017.03.005 [8] DORIGATTI I, MCCORMACK C, NEDJATI-GILANI G, et al. Using Wolbachia for dengue control: insights from modelling[J]. Trends in Parasitology, 2018, 34(2): 102-113. doi: 10.1016/j.pt.2017.11.002 [9] CHITNIS N, HYMAN J M, CUSHING J M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model[J]. Bulletin of Mathematical Biology, 2008, 70: 1272-1296. doi: 10.1007/s11538-008-9299-0 [10] 王小娥, 蔺小林, 李建全. 具有Holling IV型功能反应捕食系统的状态反馈控制[J]. 应用数学和力学, 2021, 41(12): 1369-1380. (WANG Xiaoe, LIN Xiaolin, LI Jianquan. State feedback control of predator-prey systems with holling Ⅳ functional responses[J]. Applied Mathematics and Mechanics, 2021, 41(12): 1369-1380.(in Chinese) [11] 王昕炜, 彭海军, 钟万勰. 具有潜伏期时滞的时变SEIR模型的最优疫苗接种策略[J]. 应用数学和力学, 2019, 40(7): 701-712. (WANG Xinwei, PENG Haijun, ZHONG Wanxie. Optimal vaccination strategies for a time-varying SEIR epidemic model with latent delay[J]. Applied Mathematics and Mechanics, 2019, 40(7): 701-712.(in Chinese) [12] PONTRYAGIN L S, BOLTYANSKII V G, GAMKRELIDZE R V, et al. The Mathematical Theory of Optimal Processes[M]. New Jersey: Willey, 1962. [13] LENHART S, WORKMAN J. Optimal Control Applied to Biological Models[M]. Florida: CRC Press, 2007. -
计量
- 文章访问数: 723
- HTML全文浏览量: 216
- PDF下载量: 56
- 被引次数: 0
渝公网安备50010802005915号