粒子群优化与Kriging模型相结合的结构非概率可靠性分析

乔心州; 陈永婧; 刘鹏; 方秀荣

doi:10.21656/1000-0887.420308

粒子群优化与Kriging模型相结合的结构非概率可靠性分析

doi: 10.21656/1000-0887.420308

西安科技大学机械工程学院，西安 710054

基金项目: 陕西省自然科学基础研究计划(2019JQ-796)

详细信息

作者简介:
乔心州（1974—），男，副教授，硕士生导师（通讯作者. E-mail：qiaoxinzhou@xust.edu.cn）

中图分类号: O213.2
计量
- 文章访问数: 519
- HTML全文浏览量: 247
- PDF下载量: 54
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-11
- 录用日期: 2022-03-10
- 修回日期: 2021-12-08
- 网络出版日期: 2022-11-03
- 刊出日期: 2022-12-01

Non-Probabilistic Structural Reliability Analysis Integrating the PSO and the Kriging Model

College of Mechanical Engineering, Xi’an University of Science and Technology, Xi’an 710054, P.R.China

摘要

摘要:
针对复杂结构可靠性分析中面临的隐式功能函数和小样本问题，提出了一种粒子群优化和Kriging模型相结合的结构非概率可靠性分析方法。采用多维椭球描述结构不确定参数，运用粒子群优化对模型相关参数进行求解，并构建隐式功能函数的Kriging模型进行可靠性分析。三个算例结果表明所提方法有效可行，精度和效率均优于基于Kriging模型的非概率可靠性分析方法。
- 粒子群优化 /
- Kriging模型 /
- 非概率可靠性分析
Abstract:
In view of the problems with implicit performance functions and limited experimental data in the reliability analysis of complex structures, a non-probabilistic reliability method combining the particle swarm optimization (PSO) with the Kriging model was presented. A multidimensional ellipsoid was first used to characterize the uncertain parameters of structures. The Kriging model was then constructed for the implicit performance function, wherein its optimal related parameters was determined through the PSO. Based on the proposed model the reliability analysis was explicitly conducted. The results of 3 numerical examples show that, the proposed method is of effectiveness and feasibility, and has higher accuracy and efficiency than those based on the traditional Kriging model.
- particle swarm optimization /
- Kriging model /
- non-probabilistic reliability analysis

HTML全文

图 1 线性变换与可靠性指标

Figure 1. The linear transform and the reliability index

下载: 全尺寸图片幻灯片

图 2 算法流程图

Figure 2. The flowchart for the proposed method

下载: 全尺寸图片幻灯片

图 3 相对误差对比图（算例1）

Figure 3. Comparison of relative errors (example 1)

下载: 全尺寸图片幻灯片

图 4 链轮

Figure 4. A chain wheel

下载: 全尺寸图片幻灯片

图 5 相对误差对比图（算例2）

Figure 5. Comparison of relative errors (example 2)

下载: 全尺寸图片幻灯片

图 6 25杆桁架

Figure 6. A 25-bar truss structure

下载: 全尺寸图片幻灯片

图 7 相对误差对比图（算例3）

Figure 7. Comparison of relative errors (example 3)

下载: 全尺寸图片幻灯片

表 1 相关系数为0.2的迭代过程

Table 1. The iterative process for a correlation coefficient of 0.2

iteration step	design point	reliability index
0	(−2.4442, 4.2332)	4.8882
1	(−1.8607, 4.1064)	4.5083
2	(−1.8641, 4.1039)	4.5074
reference value	(−1.8692, 4.1017)	4.5075

下载: 导出CSV

表 2 不同相关系数的可靠性指标（算例1）

Table 2. Reliability indexes for different correlation coefficients (example 1)

correlation coefficient	PSO-Kriging	iterations	CPU time	Kriging	iterations	CPU time	reference value
0	4.1704	2	0.45703 s	4.1653	5	1.00112 s	4.1701
0.2	4.5073	2	0.38524 s	4.5002	6	1.20133 s	4.5075
0.5	5.2134	3	0.68554 s	5.2039	5	1.01367 s	5.2138
0.7	5.9237	3	0.88563 s	5.9355	7	1.40156 s	5.9235
0.9	7.0337	2	0.57889 s	7.0302	6	1.16778 s	7.0339

下载: 导出CSV

表 3 相关系数为0.9的迭代过程

Table 3. The iterative process for a correlation coefficient of 0.9

iteration step	design point	reliability index
0	(0.0662, 0.0265, 0.0088, 0.00650.4059)	0.4123
1	(−0.0031, −0.0004, 0.0146, 0.0141, 0.3458)	0.3464
2	(−0.0040, −0.0005, 0.0124, 0.0176, 0.3415)	0.3422
3	(−0.0044, −0.0007, 0.00132, 0.0179, 0.3441)	0.3448
4	(−0.0042, −0.0007, 0.0134, 0.0181, 0.3439)	0.3447
reference value	(−0.0058, −0.0015, 0.0146, 0.0155, 0.3437)	0.3444

下载: 导出CSV

表 4 不同相关系数的可靠性指标（算例2）

Table 4. Reliability indexes for different correlation coefficients (example 2)

correlation coefficient	PSO-Kriging	iterations	CPU time	Kriging	iterations	CPU time	reference value
0	0.3469	4	16.15572 s	0.3406	7	27.16953 s	0.3465
0.3	0.3504	5	20.19465 s	0.3466	9	34.93226 s	0.3509
0.5	0.3517	4	17.23898 s	0.3612	7	26.35562 s	0.3513
0.7	0.3487	5	21.56773 s	0.3454	8	31.05089 s	0.3490
0.9	0.3447	4	18.06577 s	0.3404	7	28.09947 s	0.3444

下载: 导出CSV

表 5 MCS求解的95%置信区间（算例2）

Table 5. The 95% confidence intervals of MCS solutions (example 2)

MCS value	mean value	deviation	lower bound	upper bound
0.3465	0.3469	0.0029	0.3463	0.3475
0.3509	0.3506	0.0029	0.3500	0.3511
0.3513	0.3511	0.0030	0.3505	0.3517
0.3490	0.3491	0.0030	0.3485	0.3497
0.3444	0.3448	0.0031	0.3442	0.3454

下载: 导出CSV

表 6 不确定变量的分布参数

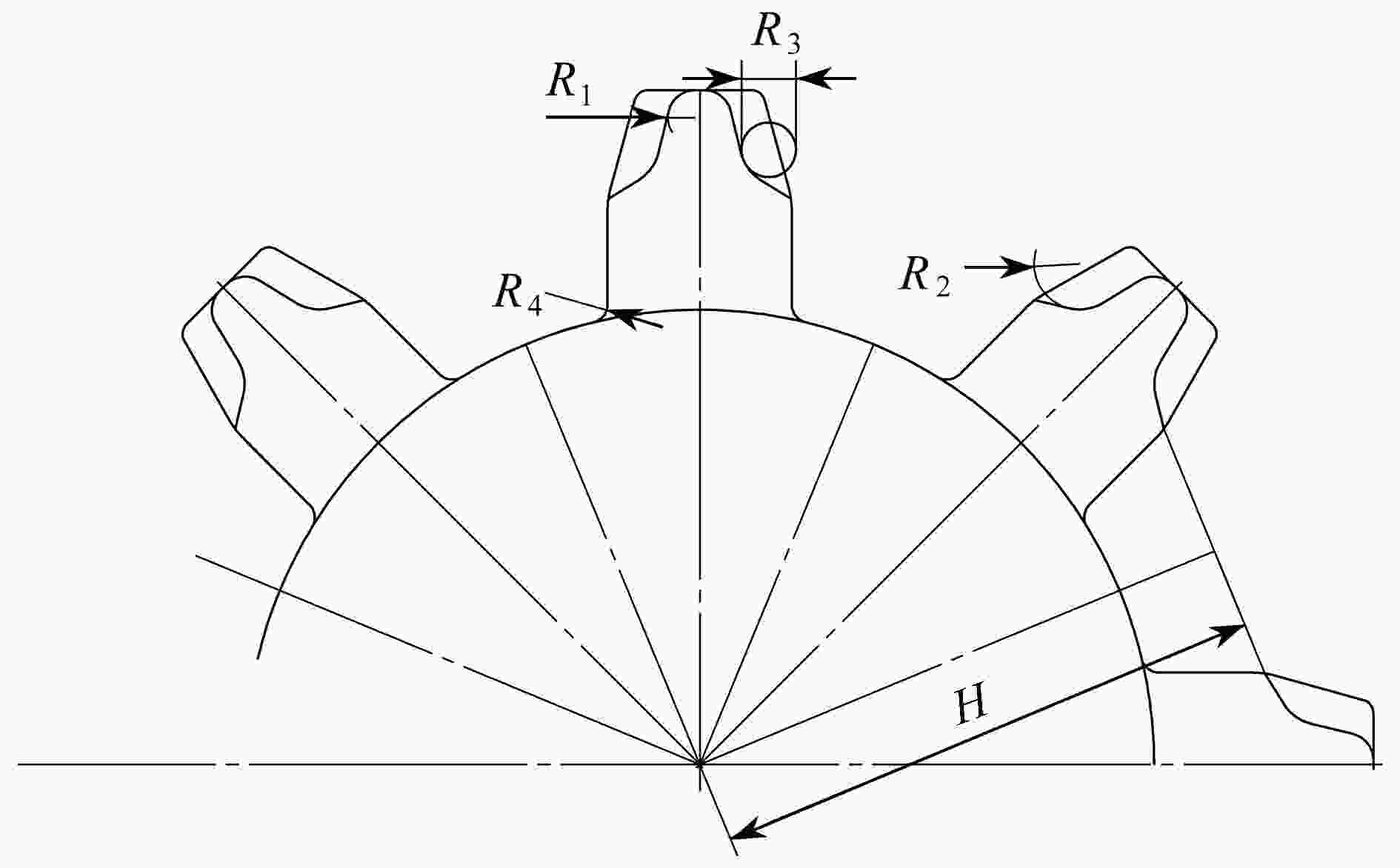
Table 6. The distribution parameters of uncertain variables

uncertain variable	mean value	radius
$ {A_1} $/mm²	700	70
$ {A_2} $/mm²	6200	620
$ {A_3} $/mm²	5300	530
$ {A_4} $/mm²	8800	880
$ L $/mm	15000	1500

下载: 导出CSV

表 7 相关系数为0的迭代过程

Table 7. The iterative process for a correlation coefficient of 0

iteration step	design point	reliability index
0	(−0.0083, −0.4266, −0.3646, −0.0519, 0.8256)	0.9997
1	(−0.0109, −0.5652, −0.4831, −0.0587, 0.9338)	1.1952
2	(−0.0100, −0.5201, −0.4446, −0.0540, 0.8593)	1.0997
3	(−0.0089, −0.4827, −0.4126, −0.0478, 0.7875)	1.0870
4	(−0.0084, −0.5107, −0.4222, −0.0509, 0.8504)	1.0793
5	(−0.0105, −0.5065, −0.4289, −0.0465, 0.8372)	1.0694
6	(−0.0094, 0.5032, −0.4301, −0.0431, 0.8356)	1.0669
reference value	(−0.0092, −0.5043, −0.4280, −0.0484, 0.8340)	1.0656

下载: 导出CSV

表 8 不同相关系数的可靠性指标（算例3）

Table 8. Reliability indexes for different correlation coefficients (example 3)

correlation coefficient	PSO-Kriging	iterations	CPU time	Kriging	iterations	CPU time	reference value
0	1.0669	6	27.02193 s	0.9944	9	37.73403 s	1.0656
0.3	1.2683	7	31.52558 s	1.1793	10	41.92578 s	1.2679
0.5	1.4906	6	28.02193 s	1.3997	10	40.44356 s	1.4917
0.7	1.9043	6	26.02193 s	1.8253	9	38.37882 s	1.9023
0.9	3.1439	7	31.52558 s	2.9934	11	46.11937 s	3.1431

下载: 导出CSV

表 9 MCS求解的95%置信区间（算例3）

Table 9. The 95% confidence intervals of MCS solutions (example 3)

MCS value	mean value	deviation	lower bound	upper bound
1.0656	1.0659	0.0029	1.0653	1.0665
1.2679	1.2672	0.0028	1.2667	1.2679
1.4917	1.4919	0.0025	1.4914	1.4924
1.9023	1.9023	0.0028	1.9017	1.9029
3.1431	3.1430	0.0029	3.1424	3.1435

下载: 导出CSV

参考文献(17)

[1]	BEN-HAIM Y. A non-probabilistic concept of reliability[J]. Structural Safety, 1994, 14(4): 227-245. doi: 10.1016/0167-4730(94)90013-2
[2]	ELISHAKOFF I, BEN-HAIM Y. Discussion on: a non-probabilistic concept of reliability[J]. Structural Safety, 1995, 17(3): 195-199. doi: 10.1016/0167-4730(95)00010-2
[3]	郭书祥, 吕震宙, 冯元生. 基于区间分析的结构非概率可靠性模型[J]. 计算力学学报, 2001, 18(1): 56-60 GUO Shuxiang, LÜ Zhengzhou, FENG Yuansheng. A non-probabilistic model of structural reliability based on interval analysis[J]. Chinese Journal of Computational Mechanics, 2001, 18(1): 56-60.(in Chinese)
[4]	JIANG T, CHEN J J, XU Y L. A semi-analytic method for calculating non-probabilistic reliability index based on interval models[J]. Applied Mathematical Modelling, 2007, 31(7): 1362-1370. doi: 10.1016/j.apm.2006.02.013
[5]	曹鸿钧, 段宝岩. 基于凸集合模型的非概率可靠性研究[J]. 计算力学学报, 2005, 22(5): 546-549, 578 CAO Hongjun, DUAN Baoyan. An approach on the non-probabilistic reliability of structures based on uncertainty convex models[J]. Chinese Journal of Computational Mechanics, 2005, 22(5): 546-549, 578.(in Chinese)
[6]	JIANG C, LU G Y, HAN X, et al. Some important issues on first-order reliability analysis with non-probabilistic convex models[J]. ASME Journal of Mechanical Design, 2014, 136(3): 034501. doi: 10.1115/1.4026261
[7]	MENG Z, HU H, ZHOU H L. Super parametric convex model and its application for non-probabilistic reliability-based design optimization[J]. Applied Mathematical Modelling, 2018, 55: 354-370. doi: 10.1016/j.apm.2017.11.001
[8]	MENG Z, ZHANG Z, ZHOU H L. A novel experimental data-driven exponential convex model for reliability assessment with uncertain-but-bounded parameters[J]. Applied Mathematical Modelling, 2020, 77(1): 773-787.
[9]	WANG X, QIU Z P, ELISHAKOFF I. Non-probabilistic set-theoretic model for structural safety measure[J]. Acta Mechanica, 2008, 198: 51-64. doi: 10.1007/s00707-007-0518-9
[10]	JIANG C, BI R G, LU G Y, et al. Structural reliability analysis using non-probabilistic convex model[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 254: 83-98. doi: 10.1016/j.cma.2012.10.020
[11]	陈江义, 文尉超, 王迎佳. 基于响应面方法的结构非概率可靠性分析[J]. 郑州大学学报(工学版), 2015, 36(5): 121-124 CHEN Jiangyi, WEN Weichao, WANG Yingjia. Analysis of structural non-probabilistic reliability based on response surface method[J]. Journal of Zhengzhou University (Engineering Science), 2015, 36(5): 121-124.(in Chinese)
[12]	BAI Y C, HAN X, JIANG C, et al. A response-surface-based structural reliability analysis method by using non-probability convex model[J]. Applied Mathematical Modelling, 2014, 38(15/16): 3834-3847.
[13]	马超, 吕震宙. 隐式极限状态方程的非概率可靠性分析[J]. 机械强度, 2009, 31(1): 45-50 doi: 10.3321/j.issn:1001-9669.2009.01.010 MA Chao, LÜ Zhengzhou. Non-probablistic reliability analysis method for implicit limit state function[J]. Journal of Mechanical Strength, 2009, 31(1): 45-50.(in Chinese) doi: 10.3321/j.issn:1001-9669.2009.01.010
[14]	潘林锋, 周昌玉, 陈士诚. 基于Kriging模型的非概率可靠度计算[J]. 应用力学学报, 2010, 27(4): 791-794 PAN Linfeng, ZHOU Changyu, CHEN Shicheng. Non-probability reliability calculation based on Kriging model[J]. Chinese Journal of Applied Mechanics, 2010, 27(4): 791-794.(in Chinese)
[15]	郑严. 基于智能算法的结构可靠性分析及优化设计研究[D]. 博士学位论文. 成都: 西南交通大学, 2012. ZHEN Yan. Research on structural reliability analysis and optimization based on intelligence algorithm[D]. PhD Thesis. Chengdu: Southwest Jiaotong University, 2012.(in Chinese)
[16]	JIANG C, HAN X, LU G Y, et al. Correlation analysis of non-probabilistic convex model and corresponding structural reliability technique[J]. Computer Methods in Applied Mechanics & Engineering, 2011, 200(33/36): 2528-2546.
[17]	屈力刚, 刘洪侠, 李铭, 等. 基于Sobol序列采样点分布策略的研究与应用[J]. 锻压装备与制造技术, 2019, 54(6): 101-105 doi: 10.16316/j.issn.1672-0121.2019.06.030 QU Ligang, LIU Hongxia, LI Ming, et al. Research and application of sampling point distribution strategy based on Sobol sequence[J]. China Metalforming Equipment & Manufacturing Technology, 2019, 54(6): 101-105.(in Chinese) doi: 10.16316/j.issn.1672-0121.2019.06.030