A Fractal Model for Thermal Dispersion Coefficients of Porous Media
-
摘要:
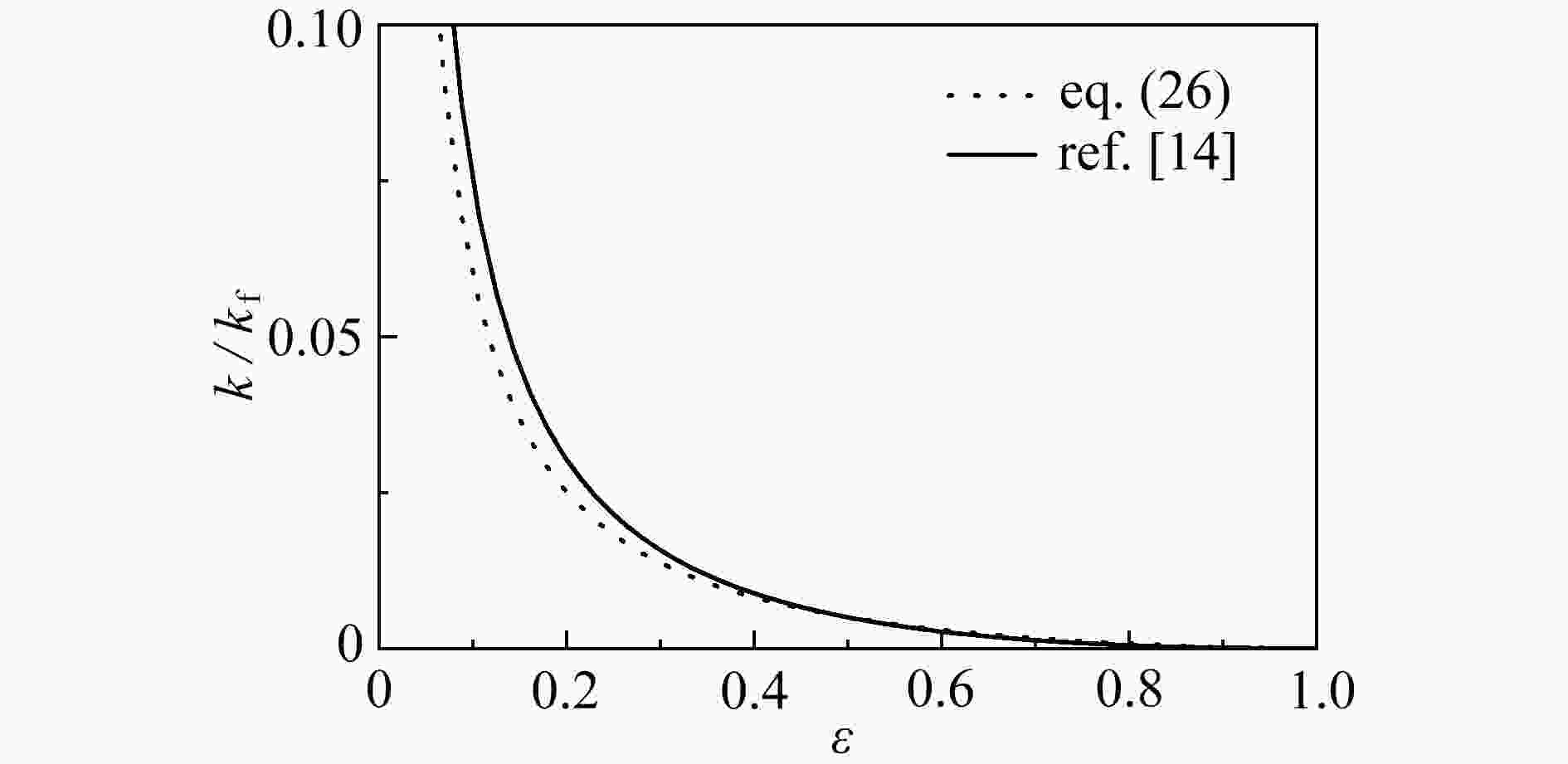
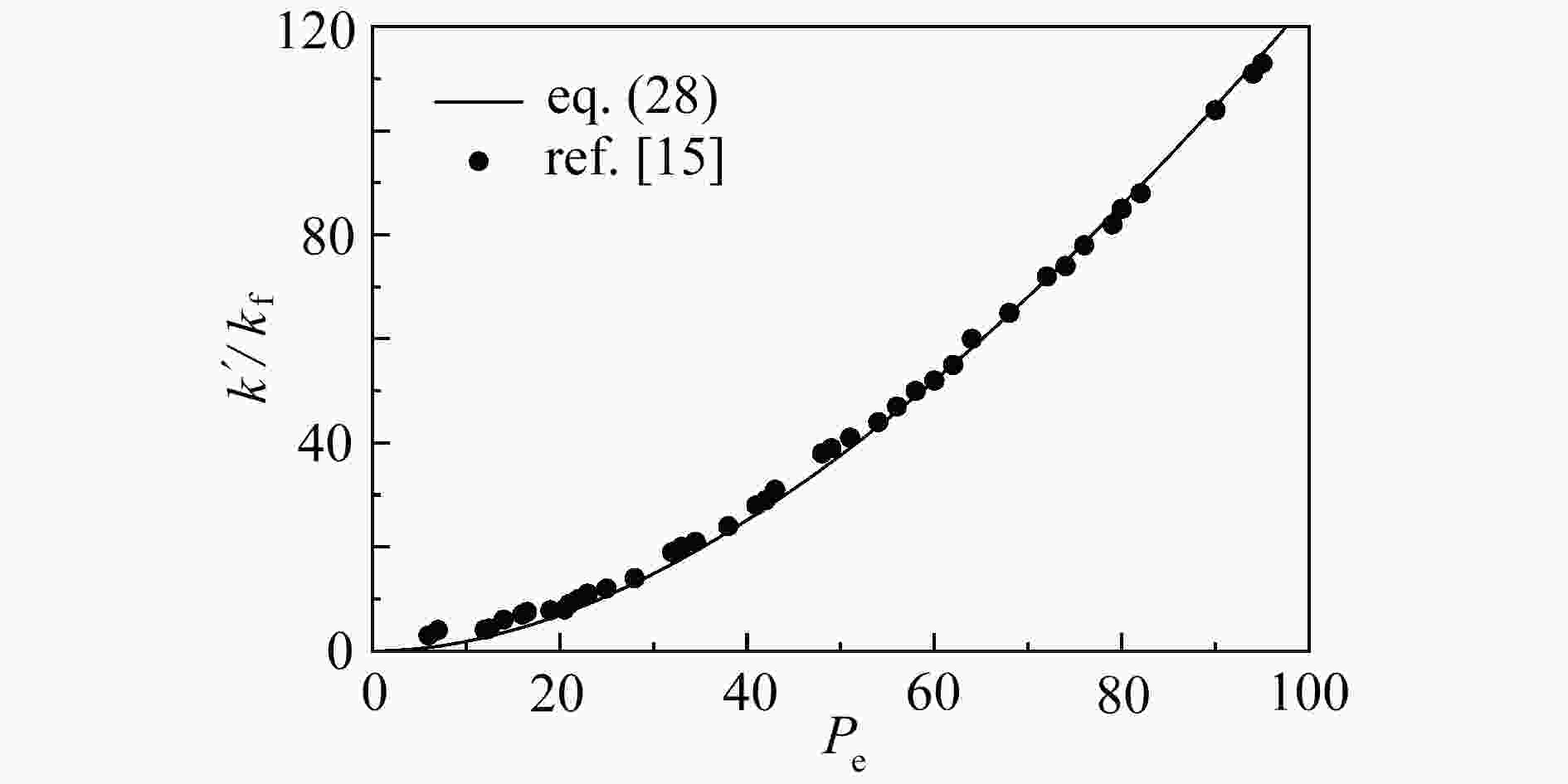
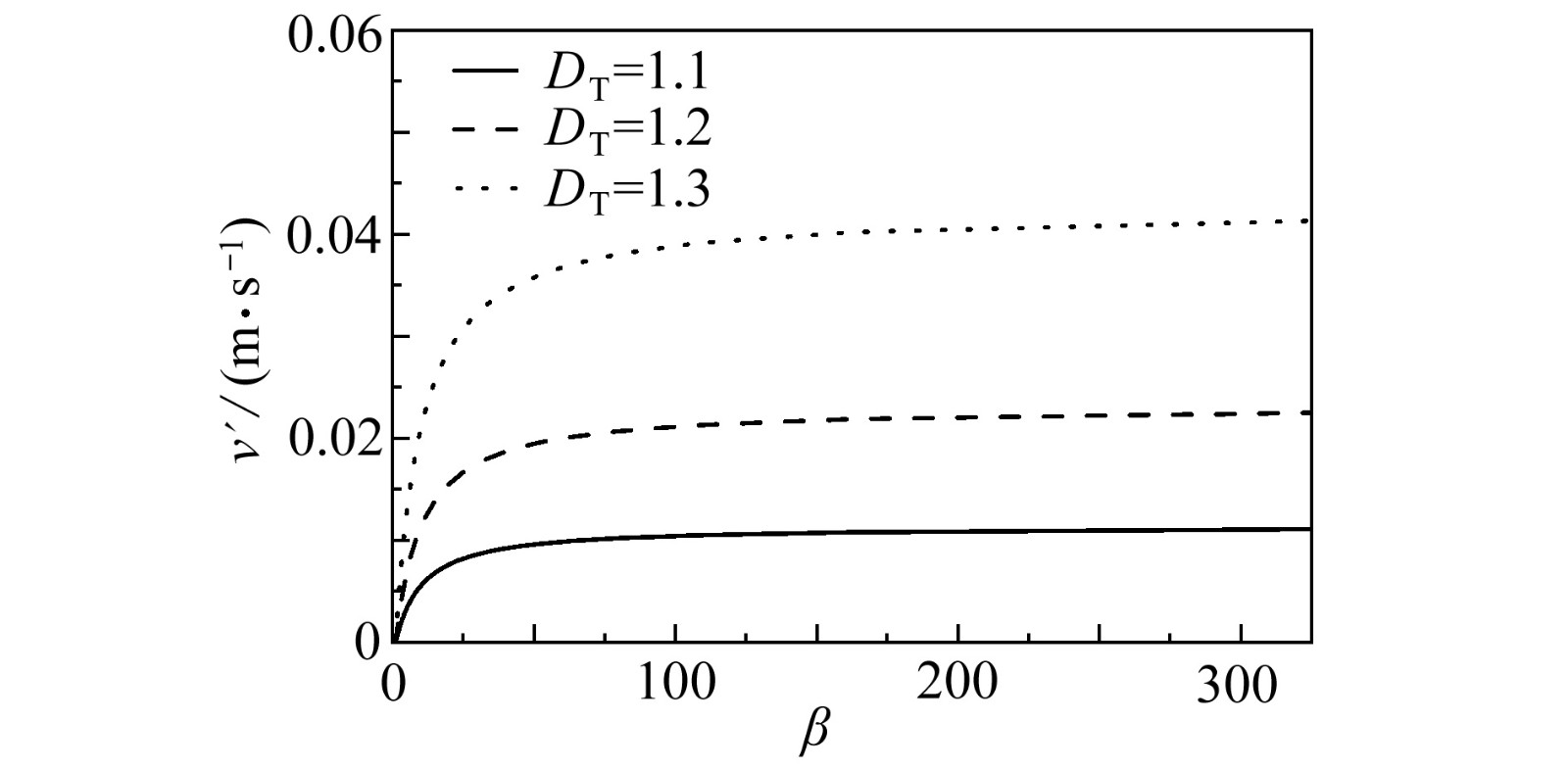
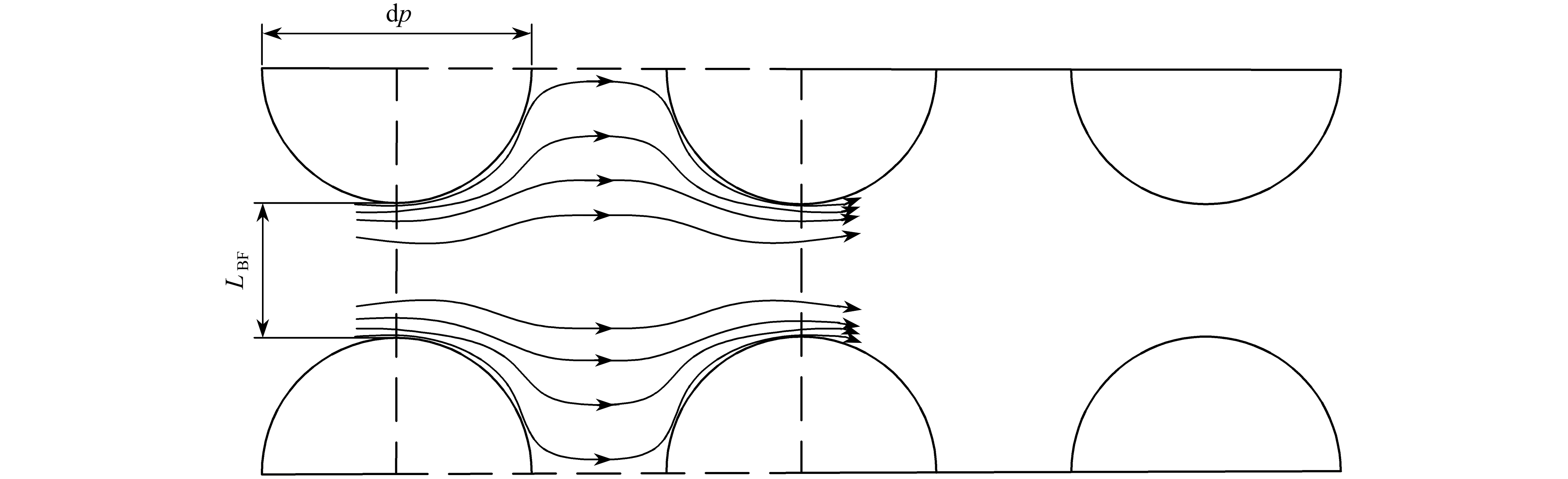
热弥散系数是与流体的物性和多孔介质结构有关的，表征多孔介质传热传质强弱的重要参数。该文建立了分形多孔介质的孔喉结构模型，研究了在孔喉结构处流体由湍流状态变为层流状态的局部水头损失和速度弥散效应，在考虑微观孔喉结构和速度弥散效应的影响下，推导了热弥散系数关系式。研究表明，热弥散系数与孔喉比、孔喉结构个数和迂曲分形维数成正比，与孔隙率和面积分形维数成反比。进一步研究发现，孔喉比在1~150范围内对速度弥散效应有显著影响，流体在孔喉结构处存在局部水头损失，导致速度弥散效应增强，热弥散系数增大。
Abstract:The thermal dispersion coefficient is an important parameter to characterize heat and mass transfer in porous media, which is related to the physical properties of fluid and the structure of porous media. The pore-throat structure model for fractal porous media was established, and the local head loss and the velocity dispersion effect were studied for the fluid changing from the turbulent state to the laminar state around the pore-throat structure. The thermal dispersion coefficient formula was derived under the influences of the micropore-throat structure and the velocity dispersion effect. The results show that, the thermal dispersion coefficient is directly proportional to the pore-throat ratio, the number of pore-throat structures and the tortuous fractal dimension, and is inversely proportional to the porosity and the area fractal dimension. Furthermore, in the range of 1~150, the pore-throat ratio has a significant influence on the velocity dispersion effect, and the fluid has a local head loss around the pore-throat structure, which leads to an enhancement of the velocity dispersion effect and an increase of the thermal dispersion coefficient.
-
Key words:
- porous media /
- pore-throat ratio /
- local head loss /
- fractal /
- heat dispersion
-
图 3 热弥散系数分形模型与常规模型对比
Figure 3. Comparison between the fractal model for the thermal dispersion coefficient and the conventional model
图 4 热弥散系数分形模型与实验值对比
Figure 4. Comparison between the fractal model for the thermal dispersion coefficient and experimental values
图 5 孔喉比对速度弥散效应的影响
Figure 5. Influences of the pore-throat ratio on the velocity dispersion effect
图 6 面积分形维数对热弥散系数的影响
Figure 6. Influences of the area fractal dimension on the thermal dispersion coefficient
图 7 迂曲分形维数对热弥散系数的影响
Figure 7. Influences of the tortuous fractal dimension on the thermal dispersion coefficient
图 8 孔喉结构个数对热弥散系数的影响
Figure 8. Influences of the number of pore-throat structures on the thermal dispersion coefficient
表 1 分形模型中部分参数与数值
Table 1. Some parameters and values in the fractal model
parameter value pore diameter λ / m 1×10−6~1×10−4 minimum pore diameter λmin / m 1×10−6 solid particles dp / m 1×10−4 viscosityµ / (Pa·s) 1.2×10−5 density ρ / (kg·m−3) 8.9×10−2 specific heat capacity cp / (J·kg−1·K−1) 1.43×104 
下载: 导出CSV
-
[1] SHOKOUHMAND H, BAGHERZADE P, FAZLI M, et al. Thermal dispersion effects on heat transfer of laminar gas flow in a microtube filled with porous medium[J]. International Journal of Thermal Sciences, 2017, 122: 281-291. doi: 10.1016/j.ijthermalsci.2017.09.002 [2] 李晓宇, 徐宏阳, 代敏, 等. 热弥散对地埋管换热器全尺度传热的影响[J]. 化工学报, 2021, 72(5): 2547-2559. (LI Xiaoyu, XU Hongyang, DAI Min, et al. Impact of thermal dispersion on full-scale heat transfer of borehole heat exchanges[J]. CIESC Journal, 2021, 72(5): 2547-2559.(in Chinese) [3] 陈仲山. 多孔介质内热质弥散及湍流预混火焰特性的双尺度研究[D]. 博士学位论文. 大连: 大连理工大学, 2015.CHEN Zhongshan. Double-scale study on heat and mass dispersion and turbulent premixed flame characteristics in porous media[D]. PhD Thesis. Dalian: Dalian University of Technology, 2015. (in Chinese) [4] 郁伯铭, 徐鹏, 邹明清, 等. 分形多孔介质输运物理[M]. 北京: 科学出版社, 2014.YU Boming, XU Peng, ZOU Mingqing, et al. Transport Physics of Fractal Porous Media[M]. Beijing: Science Press, 2014. (in Chinese) [5] 周焕林, 严俊, 余波, 等. 识别含热源瞬态热传导问题的热扩散系数[J]. 应用数学和力学, 2018, 39(2): 160-169. (ZHOU Huanlin, YAN Jun, YU Bo, et al. Identification of thermal diffusion coefficients for transient heat conduction problems with heat sources[J]. Applied Mathematics and Mechanics, 2018, 39(2): 160-169.(in Chinese) [6] JOUYBARI N F, LUNDSTRÖM T S, HELLSTRÖM J. Investigation of thermal dispersion and intra-pore turbulent heat flux in porous media[J]. International Journal of Heat and Fluid Flow, 2020, 81: 108523. doi: 10.1016/j.ijheatfluidflow.2019.108523 [7] VADASZ P. Heat flux dispersion in natural convection in porous media[J]. International Journal of Heat and Mass Transfer, 2015, 53(17/18): 3394-3404. [8] 戚涛, 胡勇, 李骞, 等. 多孔介质速度场和流量场分布[J]. 天然气地球科学, 2020, 208(3): 28-35. (QI Tao, HU Yong, LI Qian, et al. Velocity and flow field in porous media[J]. Natural Gas Geoscience, 2020, 208(3): 28-35.(in Chinese) [9] MOYNE C, DIDIERJEAN S, SOUTO H, et al. Thermal dispersion in porous media: one-equation model[J]. International Journal of Heat and Mass Transfer, 2000, 43(20): 3853-3867. [10] HUNT M L, TIEN C L. Effects of thermal dispersion on forced convection in fibrous media[J]. International Journal of Heat and Mass Transfer, 1988, 31(2): 301-309. [11] YU B M, CHENG P. A fractal permeability model for bi-dispersed porous media[J]. International Journal of Heat and Mass Transfer, 2002, 45(14): 2983-2993. [12] 张赛, 陈君若, 刘显茜. 气体有效扩散系数的分形模型[J]. 化学工程, 2013, 41(5): 39-43. (ZHANG Sai, CHEN Junruo, LIU Xianxi. Fractal model of gas effective diffusivity[J]. Chemical Engineering, 2013, 41(5): 39-43.(in Chinese) doi: 10.3969/j.issn.1005-9954.2013.05.009 [13] WU J S, YU B M. A fractal resistance model for flow through porous media[J]. International Journal of Heat and Mass Transfer, 2007, 50(19/20): 3925-3932. [14] HSU C T, CHENG P. Thermal dispersion in a porous medium[J]. International Journal of Heat and Mass Transfer, 1990, 33(8): 1587-1597. [15] METZGER T, DIDIERJEAN S, MAILLET D. Optimal experimental estimation of thermal dispersion coefficients in porous media[J]. International Journal of Heat and Mass Transfer, 2004, 47(14/16): 3341-3353. doi: 10.1016/j.ijheatmasstransfer.2004.02.024 -
计量
- 文章访问数: 774
- HTML全文浏览量: 333
- PDF下载量: 71
- 被引次数: 0
渝公网安备50010802005915号