Mesoscopic Numerical Study on Flow Boiling Heat Transfer Performance in Channels With Multiple Rectangular Heaters
-
摘要:
采用格子Boltzmann方法对恒定壁温条件下含多个矩形加热器通道内流动沸腾现象进行了数值研究。主要研究了加热器间距、加热器长度和加热器表面润湿性对气泡形态、生成气泡面积以及加热器表面热流密度大小的影响。结果表明，气泡生长速率随着加热器间距的增大而加快，较大的气泡面积促使成核气泡提前从加热器表面离开，加热器间距从250个格子增加到1000个格子时，对应的沸腾传热性能提高了12%。另一方面，加热器长度越长，气泡成核时间以及与加热器表面脱离的时间越早、沸腾传热性能越好，加热器长度从16个格子增加到22个格子时，其传热性能可以提高13%。此外, 亲水性表面的气泡成核时间晚于疏水性表面的气泡成核时间，与亲水性表面相比，疏水性表面在气泡脱离加热器之后存在残余气泡。且亲水性表面的平均热流密度和产生的气泡面积小于疏水性表面，当接触角从77°变化到120°时，其传热性能提高了26%。最后通过正交试验方案发现，加热器表面的润湿性对流动沸腾传热性能的影响最大，加热器长度对流动沸腾传热性能的影响最小。
-
关键词:
- 格子Boltzmann方法 /
- 流动沸腾 /
- 多矩形加热器
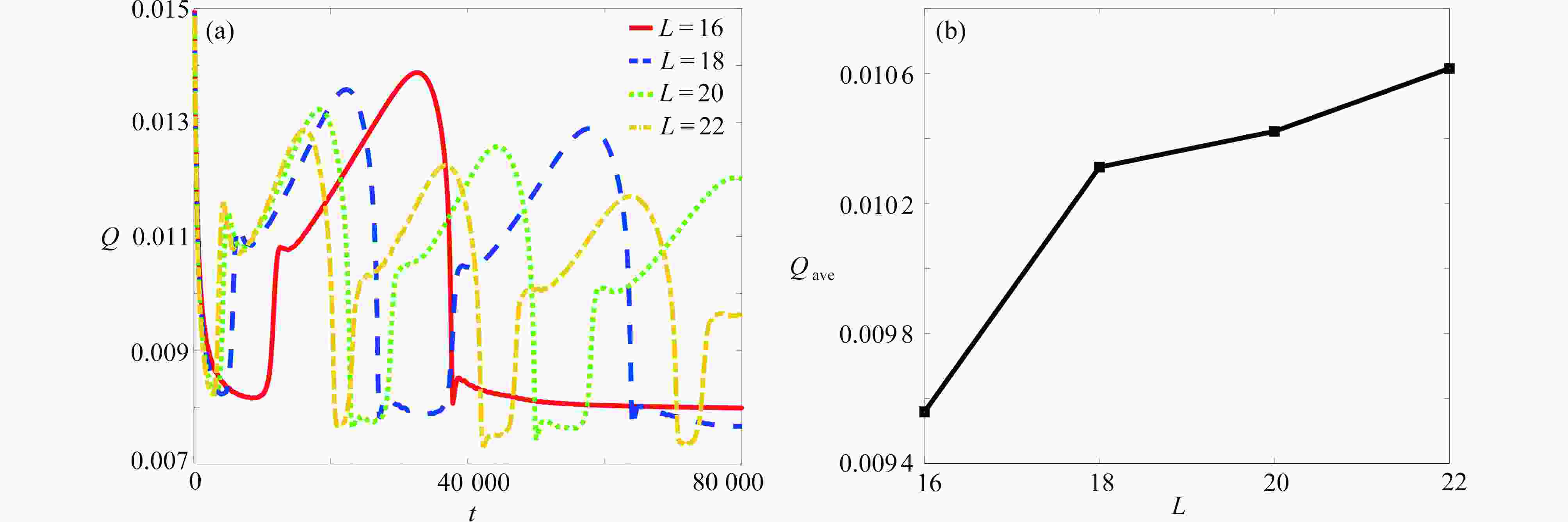
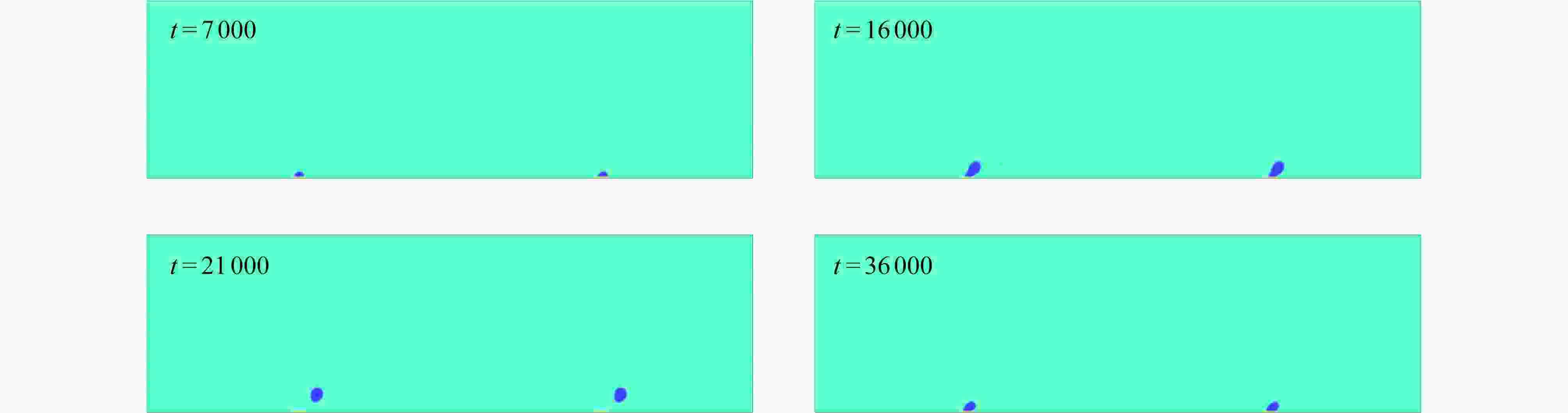
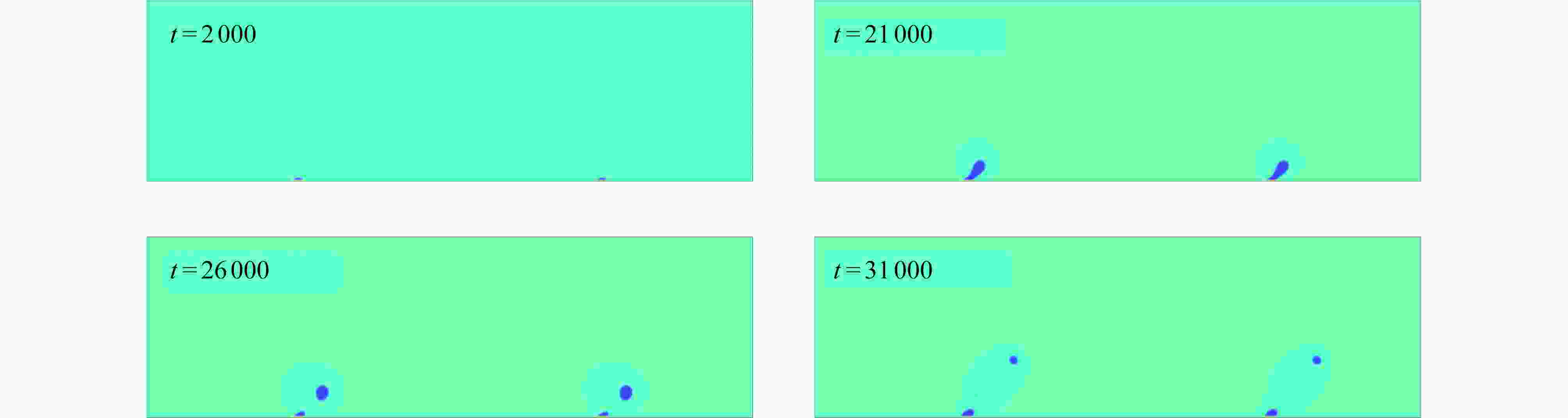
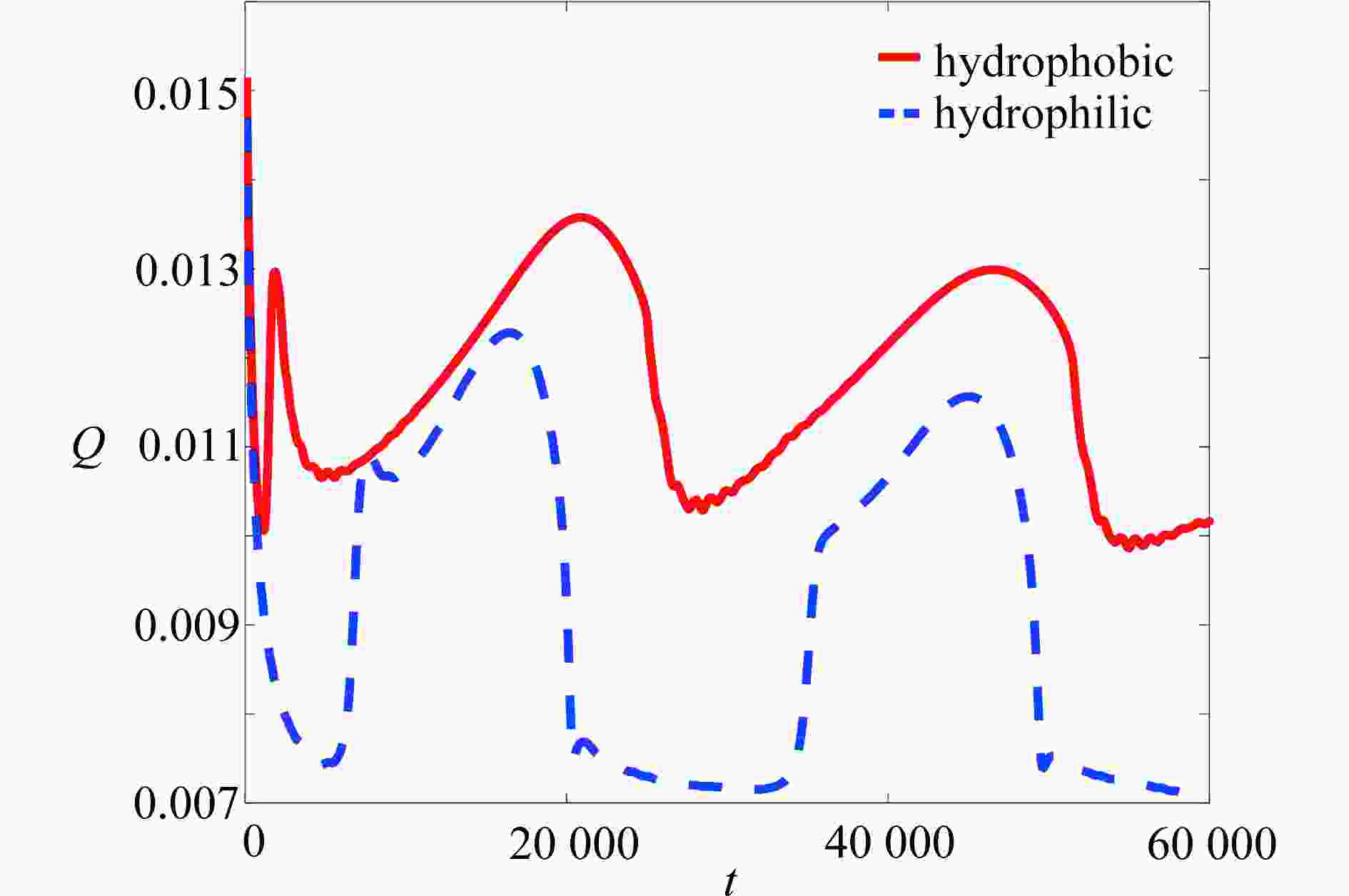
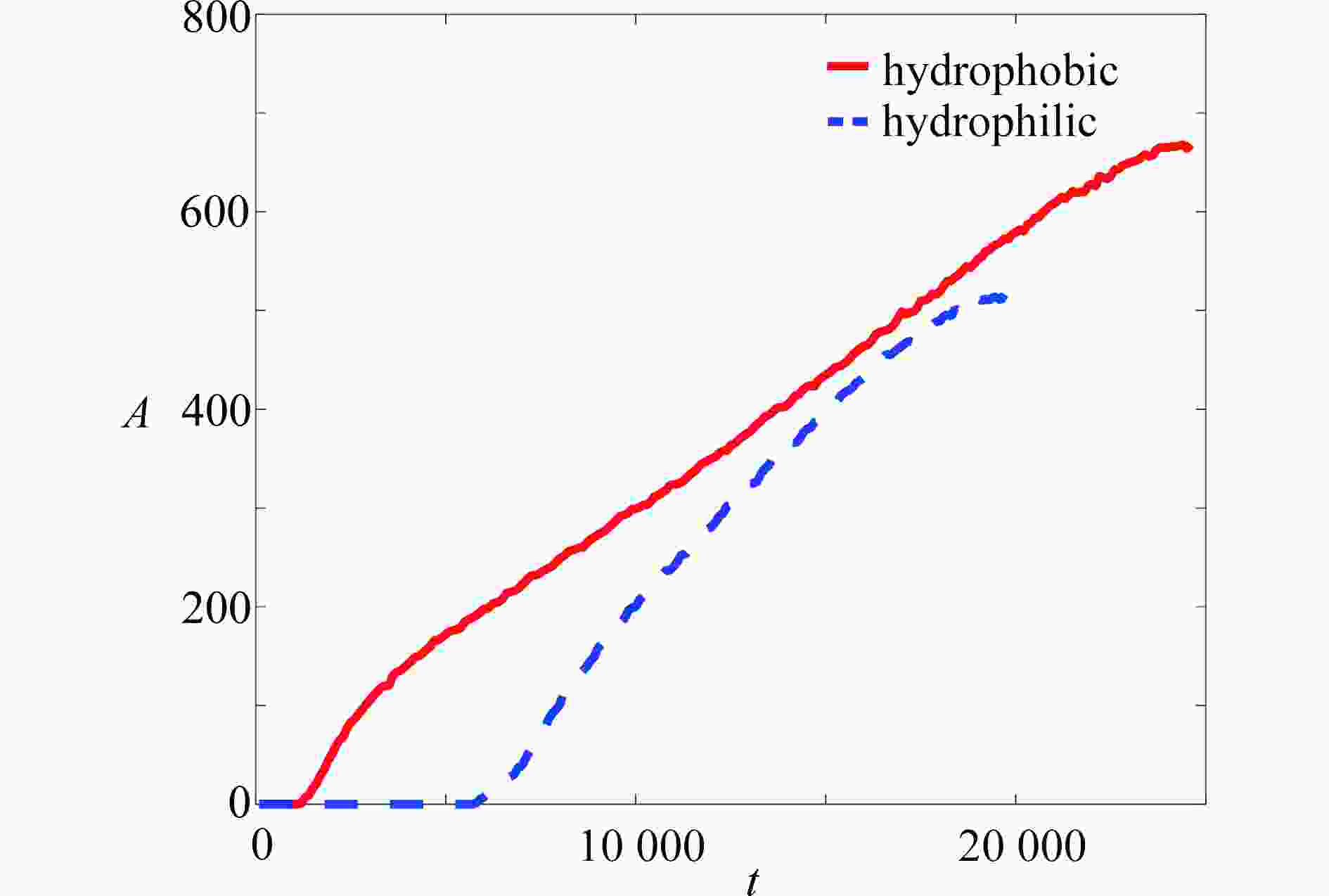
Abstract:The flow boiling phenomenon in a channel with multiple rectangular heaters under a constant wall temperature was numerically studied with the lattice Boltzmann method. The effects of spacings between heaters, heater lengths and heater surface wettabilities on the bubble morphology, the bubble area and the heat flux on the heater surface, were studied. The results show that, the bubble growth rate increases with the spacing between heaters. The larger the bubble area is, the earlier the nucleated bubbles will leave the heater surface. The corresponding boiling heat transfer performance increases by 12% with the spacing between heaters growing from 250 lattices to 1 000 lattices. On the other hand, the longer the heater length is, the earlier the bubble will nucleate and leave the heater surface, and the better the boiling heat transfer performance will be. The boiling heat transfer performance increases by 13% with the heater length rising from 16 lattices to 22 lattices. In addition, the bubble nucleates later on the hydrophilic surface than on the hydrophobic surface. Compared with the hydrophilic surface, the hydrophobic surface retains residual bubbles after the leaving of bubbles from the heater. The average heat flux and the bubble area of the hydrophilic surface are less than those of the hydrophobic surface. With the contact angle changing from 77° to 120°, the heat transfer performance increases by 26%. Finally, the orthogonal test results indicate that, the wettability of the heat exchanger surface has the greatest influence on the flow boiling heat transfer performance, while the heater length has the least influence.
-
Key words:
- lattice Boltzmann method /
- flow boiling /
- multiple rectangular heaters
-
图 2 重力加速度g与气泡脱离直径d之间的关系
Figure 2. The relationship between gravitational acceleration g and bubble departure diameter d
图 4 不同加热器间距时计算域的密度分布：（a）D=500；（b）D=333；（c）D=250
Figure 4. Density distributions with different heater spacings: (a)D=500; (b) D=333; (c) D=250
图 6 不同加热器间距下加热器表面平均热流密度的变化：（a）加热器表面空间平均热流密度随时间的变化；（b）加热器表面空间-时间平均热流密度
Figure 6. Heat fluxes on the heater surface with different heater spacings: (a) temporal variations of the spatial average heat flux on the heater surface; (b) the temporal and spatial average heat flux on the heater surface
图 7 不同加热器长度时计算域的密度分布：（a）L=16；（b）L=18；（c）L=20；（d）L=22
Figure 7. Density distributions with different heater lengths: (a) L=16; (b) L=18; (c) L=20; (d) L=22
图 9 不同加热器长度下加热器表面平均热流密度的变化：（a）加热器表面空间平均热流密度随时间的变化；（b）加热器表面空间-时间平均热流密度
Figure 9. Heat fluxes on the heater surface with different heater lengths: (a) temporal variations of the spatial average heat flux on the heater surface; (b) the temporal and spatial average heat flux on the heater surface
图 10 亲水性表面（θ=77°）时计算域的密度分布
Figure 10. Density distributions on the hydrophilic surface（θ=77°）
图 11 疏水性表面（θ=120°）时计算域的密度分布
Figure 11. Density distributions on the hydrophobic surface（θ=120°）
图 12 不同润湿性表面下加热器表面平均热流密度随时间的变化
Figure 12. Temporal variations of the spatial average heat flux on the heater surface with different wettabilities
表 1 网格无关性
Table 1. Grid independence
mesh size mean heat flux Qave Lx × Ly=500 × 150 1.027 × 10−2 Lx × Ly=1000 × 300 1.179 × 10−2 Lx × Ly=2000 × 600 1.184 × 10−2 
下载: 导出CSV
表 2 正交试验表及数据分析
Table 2. The orthogonal test table and data analysis
test number length L distance D contact angle θ test index （mean heat flux） Qave 1 18（①） 333（①） 77°（①） 8.463 × 10−3 2 18（①） 500（②） 90°（②） 1.043 × 10−2 3 18（①） 1000（③） 120°（③） 1.264 × 10−2 4 20（②） 333（①） 90°（②） 1.032 × 10−2 5 20（②） 500（②） 120°（③） 1.273 × 10−2 6 20（②） 1000（③） 77°（①） 9.856 × 10−3 7 22（③） 333（①） 120°（③） 1.327 × 10−2 8 22（③） 500（②） 77°（①） 9.087 × 10−3 9 22（③） 1000（③） 90°（②） 1.116 × 10−2 A 1.051 × 10−2 1.069 × 10−2 9.135 × 10−3 – B 1.097 × 10−2 1.075 × 10−2 1.064 × 10−2 – C 1.117 × 10−2 1.122 × 10−2 1.288 × 10−2 – R 6.611 × 10−4 5.353 × 10−4 3.748 × 10−3 –
下载: 导出CSV
-
[1] KANG M. Effect of surface roughness on pool boiling heat transfer[J]. International Journal of Heat and Mass Transfer, 2000, 43(22): 4073-4085. doi: 10.1016/S0017-9310(00)00043-0 [2] GOEL P, NAYAK A K, KULKARNI P P, et al. Experimental study on bubble departure characteristics in subcooled nucleate pool boiling[J]. International Journal of Multiphase Flow, 2017, 89: 163-176. doi: 10.1016/j.ijmultiphaseflow.2016.10.012 [3] HE H, LIU Y, LIU L, et al. Numerical simulation of bubble growth on and departure from the heated surface by an improved lattice Boltzmann model[J]. Kerntechnik, 2018, 83: 186-192. doi: 10.3139/124.110877 [4] GONG S, CHENG P. A lattice Boltzmann method for simulation of liquid-vapor phase-change heat transfer[J]. International Journal of Heat and Mass Transfer, 2012, 55(17/18): 4923-4927. doi: 10.1016/j.ijheatmasstransfer.2012.04.037 [5] WANG H, LOU Q, LI L. Mesoscale simulations of saturated flow boiling heat transfer in a horizontal microchannel[J]. Numerical Heat Transfer(Part A) : Applications, 2020, 78(4): 107-124. doi: 10.1080/10407782.2020.1786290 [6] DONG Z, XU J, JIANG F, et al. Numerical study of vapor bubble effect on flow and heat transfer in microchannel[J]. International Journal of Thermal Sciences, 2012, 54: 22-32. doi: 10.1016/j.ijthermalsci.2011.11.019 [7] NIE D, GUAN G. Study on boiling heat transfer in a shear flow through the lattice Boltzmann method[J]. Physics of Fluids, 2012, 33: 043314. [8] GONG S, CHENG P. Numerical investigation of saturated flow boiling in microchannels by the lattice Boltzmann method[J]. Numerical Heat Transfer(Part A) : Applications, 2014, 65: 644-661. doi: 10.1080/10407782.2013.836025 [9] TAN K, HU Y, HE Y. Effect of wettability on flow boiling heat transfer in a microtube[J]. Case Studies in Thermal Engineering, 2021, 26: 101018. doi: 10.1016/j.csite.2021.101018 [10] YIN X, TIAN Y, ZHOU D, et al. Numerical study of flow boiling in an intermediate-scale vertical tube under low heat flux[J]. Applied Thermal Engineering, 2019, 153: 739-747. doi: 10.1016/j.applthermaleng.2019.03.067 [11] AZIZIFAR S, AMERI M, IMAN B. An experimental study of subcooled flow boiling of water in the horizontal and vertical direction of a metal-foam tube[J]. Thermal Science and Engineering Progress, 2020, 20(1): 100748. [12] WANG J, CHENG Y, LI X B, et al. Experimental and LBM simulation study on the effect of bubbles merging on flow boiling[J]. International Journal of Heat and Mass Transfer, 2019, 132: 1053-1061. doi: 10.1016/j.ijheatmasstransfer.2018.11.140 [13] VONTAS K, ANDREDAKI M, GEORGOULAS A, et al. The effect of surface wettability on flow boiling characteristics within microchannels[J]. International Journal of Heat and Mass Transfer, 2021, 172: 121133. doi: 10.1016/j.ijheatmasstransfer.2021.121133 [14] SUN T, GUI N, YANG X, et al. Numerical study of patterns and influencing factors on flow boiling in vertical tubes by thermal LBM simulation[J]. International Communications in Heat and Mass Transfer, 2017, 86: 32-41. doi: 10.1016/j.icheatmasstransfer.2017.05.014 [15] YADAV A, ROY S. Void fraction distribution for convective boiling flows in single and multiple heater rods assembly[J]. Chemical Engineering Science, 2022, 247: 117063. doi: 10.1016/j.ces.2021.117063 [16] BALTIS C, GELD C. Experimental investigation of the thermal interactions of nucleation sites in flow boiling[J]. International Journal of Heat and Mass Transfer, 2014, 78(11): 1208-1218. [17] CHENG M, ZHANG B, LOU J. A hybrid LBM for flow with particles and drops[J]. Computers & Fluids, 2017, 155(20): 62-67. [18] SONG F, WANG W, LI J. A lattice Boltzmann method for particle-fluid two-phase flow[J]. Chemical Engineering Science, 2013, 102: 442-450. doi: 10.1016/j.ces.2013.08.037 [19] LI Q, KANG Q, FRANCOIS M, et al. Lattice Boltzmann modeling of boiling heat transfer: the boiling curve and the effects of wettability[J]. International Journal of Heat and Mass Transfer, 2015, 85: 787-796. doi: 10.1016/j.ijheatmasstransfer.2015.01.136 [20] YUAN P, SCHAEFER L. Equations of state in a lattice Boltzmann model[J]. Physics of Fluids, 2006, 18: 042101. doi: 10.1063/1.2187070 [21] ZHANG T, SHI B, GUO Z, et al. General bounce-back scheme for concentration boundary condition in the lattice-Boltzmann method[J]. Physical Review E, 2012, 85: 016701. doi: 10.1103/PhysRevE.85.016701 [22] FRITZ W. Berechnung des maximal volumes von Dampfblasen[J]. Physik Zeitschr, 1935, 36: 379-384. [23] FENG Y, CHANG F, HU Z, et al. Investigation of pool boiling heat transfer on hydrophilic-hydrophobic mixed surface with micro-pillars using LBM[J]. International Journal of Thermal Sciences, 2021, 163: 106814. doi: 10.1016/j.ijthermalsci.2020.106814 [24] GONG S, CHENG P. Lattice Boltzmann simulations for surface wettability effects in saturated pool boiling heat transfer[J]. International Journal of Heat and Mass Transfer, 2015, 85: 635-646. doi: 10.1016/j.ijheatmasstransfer.2015.02.008 [25] GONG S, CHENG P. Lattice Boltzmann simulation of periodic bubble nucleation, growth and departure from a heated surface in pool boiling[J]. International Journal of Heat and Mass Transfer, 2013, 64: 122-132. doi: 10.1016/j.ijheatmasstransfer.2013.03.058 -
计量
- 文章访问数: 528
- HTML全文浏览量: 303
- PDF下载量: 49
- 被引次数: 0
渝公网安备50010802005915号