Structural Crack Identification Based on the Variational Mode Decomposition
-
摘要:
为完善桥梁损伤检测方法，进一步提高桥梁损伤识别的精度，以动载作用下带裂纹简支梁模型为研究对象，提出了一种不基于完整有限元模型的裂纹检测方法。该方法在不阻塞交通的前提下，仅需对简支梁跨中加速度响应进行分析处理，减少了实际工程中传感器的装卸及维护工作。同时，基于该模型推导出了简支裂纹梁跨中加速度解析式。在理论推导的支撑下，利用变分模态分解和Hilbert变换构造出了瞬时能量和均值能量差，这两个裂纹识别指标能够有效地识别出裂纹深度占比为5%的小裂纹。基于此，开展了不同轮载大小、环境噪声以及损伤程度对检测结果影响的研究。结果表明：① 瞬时频率对裂纹位置具有较好的识别效果；② 均值能量差对不同裂纹深度占比以及轮载大小具有一定的敏感度；③ 该方法具有较强的噪声鲁棒性。
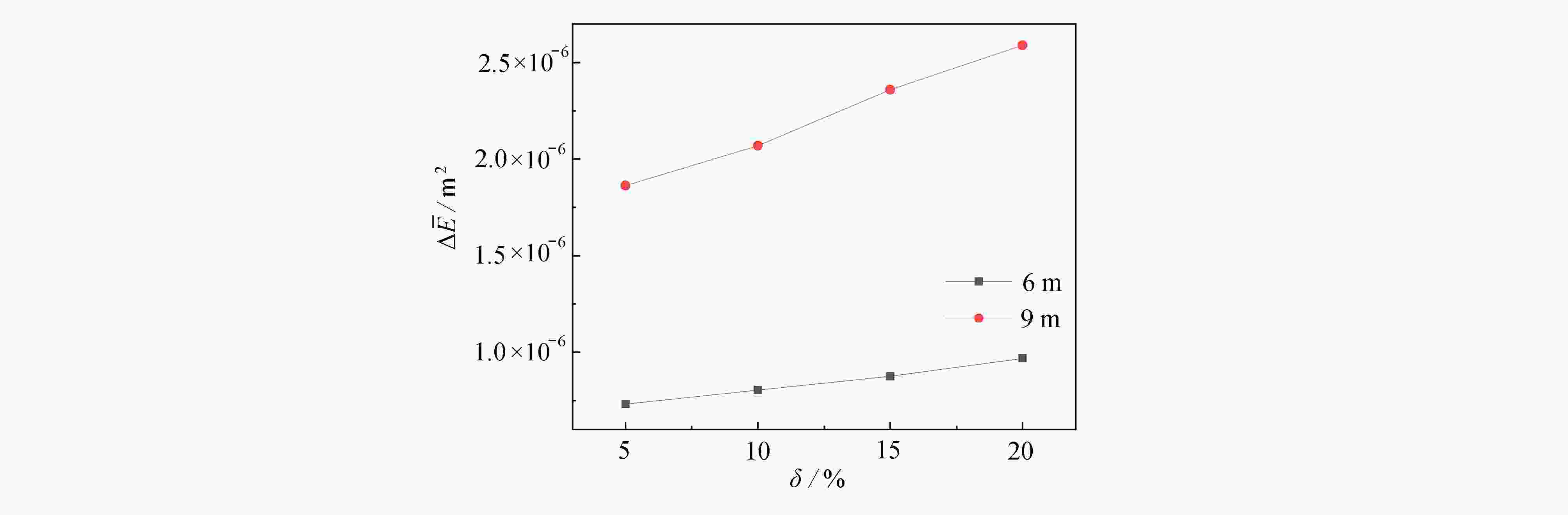
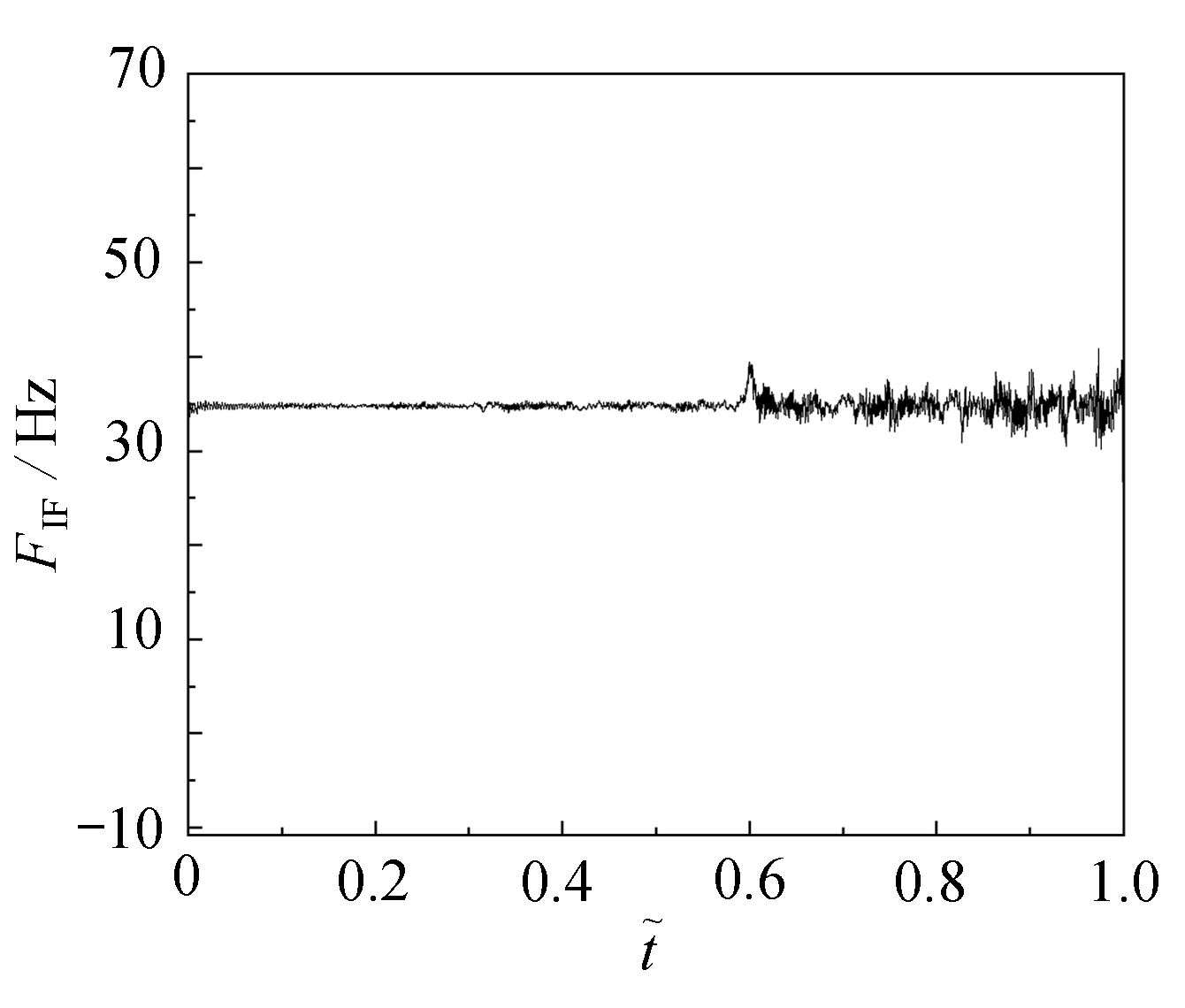
Abstract:In order to enrich the bridge damage detection method and further improve the accuracy of bridge damage identification, a detection method for simply supported beams with cracks under dynamic loads was proposed not based on the complete finite element model. Under the premise of not blocking traffic, the method only needs to analyze and deal with the acceleration responses of the simply supported beam span, which reduces the mounting, dismounting and maintenance of sensors in practical engineering. At the same time, based on the model, an analytical formula of the acceleration at the midspan of the simply supported cracked beam was derived. Based on the theoretical derivation, the instantaneous energy and the mean energy difference were constructed through the variational mode decomposition and the Hilbert transform, and these 2 crack identification indexes were used to effectively identify small cracks with a crack depth ratio of only 5%. Then the influences of different wheel loads, environmental noises and damage degrees on detection results were studied. The results show that: ① the instantaneous frequency has a better recognition effect for crack positions; ② the mean energy difference is sensitive to crack depth ratio δ and the wheel load magnitude; ③ this method has strong noise robustness.
-
图 5 车轮荷载：（a） 集中荷载；（b） 非均布荷载
Figure 5. The wheel load: (a) a concentrated load; (b) an ununiform load
图 9
$ \delta $ 为2$ 0\text{%} $ ，15$ \text{%} $ ，$ 10\text{%} $ ，5$ \text{%} $ 的瞬时频率对比Figure 9. Comparison of instantaneous frequencies for
$\delta $ = 20%, 15%, 10%, 5%
图 10
$ \delta $ 为$ 20\text{%} $ ，15$ \text{%} $ ，$ 10\text{%} $ ，5$ \text{%} $ 的瞬时能量对比Figure 10. Comparison of instantaneous energy for
$\delta $ = 20%, 15%, 10%, 5%
图 12 三种轮载大小作用下瞬时能量对比
Figure 12. Comparison of instantaneous energies under 3 wheel loads
图 14
$ \delta $ 为2$ 0\text{%} $ ，15$ \text{%} $ ，$ 10\text{%} $ ，5$ \text{%} $ 的瞬时频率对比（双位置）Figure 14. Comparison of instantaneous frequencies for
$\delta $ = 20%, 15%, 10%, 5% (2 positions)
图 15
$ \delta $ 为$ 20\text{%} $ ，15$ \text{%} $ ，$ 10\text{%} $ ，5$ \text{%} $ 的瞬时能量对比（双位置）Figure 15. Comparison of instantaneous energy for
$\delta $ = 20%, 15%, 10%, 5% (2 positions)表 1 模拟工况
Table 1. The simulation condition
condition elastic modulus
Et /($ {\rm{N}}/{{\rm{m}}}^{3} $)density
$ \rho $/($ {\rm{kg}}/{{\rm{m}}}^{3} $)Poisson’s ratio $ \mu $ moving load
velocity $ V/({\rm{km/h}} )$wheel load
P $/{\rm{kN} }$crack location
$ {L}_{1} $/mcrack depth
ratio $ \delta $ = d/H1 $ 4.54\times {10}^{10} $ $ 2\;549 $ $ 0.2 $ $ 6 $ $ 10 $ $ 9 $ 0.15 
下载: 导出CSV
-
[1] ZHU J, ZHANG Y. Damage detection in bridge structures under moving vehicle loads using delay vector variance method[J]. Journal of Performance of Constructed Facilities, 2019, 33(5): 4019049. [2] ZHU X Q, LAW S S. Wavelet-based crack identification of bridge beam from operational deflection time history[J]. International Journal of Solids and Structures, 2006, 43(7): 2299-2317. [3] 刘光耀, 刘习军, 张素侠, 等. 基于小波分析和变异系数的简支梁桥损伤识别[J]. 应用力学学报, 2020, 37(5): 1915-1922LIU Guangyao, LIU Xijun, ZHANG Suxia, et al. Damage identification of simply supported beam bridge based on wavelet analysis and variation coefficient[J]. Chinese Journal of Applied Mechanics, 2020, 37(5): 1915-1922.(in Chinese) [4] KHORRAM A, BAKHTIARI-NEJAD F, REZAEIAN M. Comparison studies between two wavelet based crack detection methods of a beam subjected to a moving load[J]. International Journal of Engineering Science, 2012, 51: 204-215. doi: 10.1016/j.ijengsci.2011.10.001 [5] 刘小靖, 周又和, 王记增. 小波方法及其力学应用研究进展[J]. 应用数学和力学, 2022, 43(1): 1-13 doi: 10.1007/s10483-021-2795-5LIU Xiaojing, ZHOU Youhe, WANG Jizeng. Research progresses of wavelet methods and their applications in mechanics[J]. Applied Mathematics and Mechanics, 2022, 43(1): 1-13.(in Chinese) doi: 10.1007/s10483-021-2795-5 [6] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. doi: 10.1098/rspa.1998.0193 [7] MEREDITH J, GONZÁLEZ A, HESTER D. Empirical mode decomposition of the acceleration response of a prismatic beam subject to a moving load to identify multiple damage locations[J]. Shock and Vibration, 2012, 19(5): 845-856. doi: 10.1155/2012/804590 [8] ROVERI N, CARCATERRA A. Damage detection in structures under traveling loads by Hilbert-Huang transform[J]. Mechanical Systems and Signal Processing, 2012, 28: 128-144. doi: 10.1016/j.ymssp.2011.06.018 [9] 孟宗, 季艳, 谷伟明, 等. 基于支持向量机和窗函数的DEMD端点效应抑制方法[J]. 计量学报, 2016, 37(2): 180-184MENG Zong, JI Yan, GU Weiming, at el. End effects restraining of DEMD based on support vector machine and window function[J]. Acta Metrologica Sinica, 2016, 37(2): 180-184.(in Chinese) [10] 邢昀, 荣剑. 常见不同模态信号分解方法探讨[J]. 现代计算机, 2018, 36: 7-11XING Yun, RONG Jian. Discussion on the signal decomposition methods of common modes[J]. Modern Computer, 2018, 36: 7-11.(in Chinese) [11] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. doi: 10.1109/TSP.2013.2288675 [12] 赵岩, 朱均超, 张宝峰, 等. 基于VMD与Hilbert谱的旋转机械碰摩故障诊断方法[J]. 振动、测试与诊断, 2018, 38(2): 381-386 doi: 10.16450/j.cnki.issn.1004-6801.2018.02.026ZHAO Yan, ZHU Junchao, ZHANG Baofeng, et al. Rub-impact fault diagnosis of rotating machinery based on VMD and Hilbert spectrum[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(2): 381-386.(in Chinese) doi: 10.16450/j.cnki.issn.1004-6801.2018.02.026 [13] 唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5): 73-81 doi: 10.7652/xjtuxb201505012TANG Guiji, WANG Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J]. Journal of Xi’an Jiaotong University, 2015, 49(5): 73-81.(in Chinese) doi: 10.7652/xjtuxb201505012 [14] 赵昕海, 张术臣, 李志深, 等. 基于VMD的故障特征信号提取方法[J]. 振动、测试与诊断, 2018, 38(1): 11-19ZHAO Xinhai, ZHANG Shuchen, LI Zhishen, et al. Application of new denoising method based on VMD in fault feature extraction[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(1): 11-19.(in Chinese) [15] BAGHERI A, ALIPOUR M, OZBULUT O E, et al. Identification of flexural rigidity in bridges with limited structural information[J]. Journal of Structural Engineering, 2018, 144(8): 4018126. doi: 10.1061/(ASCE)ST.1943-541X.0002131 [16] 王超, 毛羚. 基于VMD和广义Morse小波的结构瞬时频率识别[J]. 振动、测试与诊断, 2020, 40(5): 957-962WANG Chao, MAO Ling. Instantaneous frequency identification of a structure using variational mode decomposition and generalized Morse wavelets[J]. Journal of Vibration, Measurement & Diagnosis, 2020, 40(5): 957-962.(in Chinese) [17] MOUSAVI M, HOLLOWAY D, OLIVIER J C, et al. Beam damage detection using synchronisation of peaks in instantaneous frequency and amplitude of vibration data[J]. Measurement, 2021, 168: 1-14. [18] CHONDROS T G, DIMAROGONAS A D, YAO J. A continuous cracked beam vibration theory[J]. Journal of Sound and Vibration, 1998, 215(1): 17-34. doi: 10.1006/jsvi.1998.1640 [19] 王扬. 复杂轮胎力作用下沥青路面力学行为研究[D]. 博士学位论文. 北京: 北京交通大学, 2017.WANG Yang. Study on mechanical behaviors of asphalt pavement under complicated tire force[D]. PhD Thesis. Beijing: Beijing Jiaotong University, 2017. (in Chinese) -
点击查看大图
计量
- 文章访问数: 341
- HTML全文浏览量: 154
- PDF下载量: 42
- 被引次数: 0
