Effects of Time Delay on Bifurcation and Synchronization of Flux-Coupled and Chemically Coupled Neurons
-
摘要:
以化学突触耦合神经元模型为基础,讨论了抑制性及兴奋性条件下达到同步的区别及同步的类型。并根据磁通耦合对神经元放电的影响,讨论了具有时滞、磁通耦合和化学耦合Morris-Lecar (ML)神经元模型的放电状态、分岔类型及其同步情况。发现具有磁通耦合和化学耦合ML神经元系统在不同参数下会产生丰富的逆倍周期分岔或加周期分岔行为。而时滞的引入,虽然可以增加系统的周期性,但同时也会破环系统同步。相反,适当的耦合强度能够增加同步。
Abstract:Based on the chemical synaptic coupled neuron model, the differences and types of synchronization under inhibitory and excitatory conditions were discussed. According to the effect of the magnetic flow coupling on neuron discharge, the discharge states, bifurcation types and synchronization of the Morris-Lecar (ML) neuron models with time delay, magnetic flux coupling and chemical coupling, were analyzed. The results show that, the ML neuronal systems with magnetic flow coupling and chemical coupling can produce rich inverse periodic bifurcation or incremental periodic bifurcation behaviors under different parameters. The introduction of time delay, although can increase the periodicity of the system, will also break the system synchronization. Conversely, an appropriate coupling strength can enhance synchronization.
-
Key words:
- time delay /
- flux-coupled /
- bifurcation /
- synchronization
-
引 言
神经元是神经系统的基本单位,神经元的基本结构有胞体、树突和轴突,主要通过突触进行信息传递,其中化学突触是一种主要的信息传递方式,通过突触前膜释放神经递质,刺激突触后膜产生动作电位,在神经元之间进行信息传递[1]。文献[2]研究了化学突触中时滞及耦合强度对耦合神经元系统同步的影响,揭示了时滞对耦合神经元同步有促进作用。由于细胞间各带电离子进行跨膜运动时产生的放电行为会在细胞周围产生小范围的磁场,影响神经元的电位变化,而电位的变化又会引起磁场的改变,导致神经元之间信息传递始终处于一个微弱磁场当中,这势必会对其放电模式及其同步状态产生影响[3]。Ma等[4-5]通过对单个神经元模型在电磁辐射下的多模式放电行为的研究,揭示了电磁对神经元放电的影响。文献[6]揭示了周期电磁刺激对单个神经元和神经元网络系统动力学行为的显著调控能力。文献[7]研究了磁流对化学突触与电突触神经元系统同步的影响。Guo等[8]在改进的电磁感应神经元模型基础上,研究了链式连接下耦合神经元模型的场耦合效应,揭示了稳定性与耦合强度之间的关系。然而突触间总存在着间隙,使神经元信息之间的传递总存在着一定的延迟,这种现象称之为时滞[9]。时滞的出现,使原本神经系统从有限维转变为无限维,使其本身复杂的动力学行为研究更具有挑战性,国内外学者纷纷在这方面进行探索与研究。文献[10]研究了传导延迟对具有抑制性突触神经元系统破裂同步的影响,揭示了只有通过传导延迟来抑制混沌,才能有效增强耦合系统的同步。文献[11]研究了两个具有时滞的突触耦合FHN神经元的分岔和同步问题,揭示了随着时滞的引入,耦合神经元会出现由混沌运动向周期运动的过渡,并且小的时间延迟可以产生新的周期窗口。Wang等[12]通过对引入时滞的耦合混沌Morris-Lecar (ML)神经元同步研究,发现时滞不仅能提高耦合神经元的同步,还能引发其丰富的放电模式。
为观察化学突触、电磁和时滞等作用对神经元动力学特性的影响,本文在ML神经元模型的基础上,首先通过化学突触耦合,建立耦合神经元系统,运用相似函数,通过数值模拟方法,探究抑制性与兴奋性化学突触对耦合系统同步的影响,并用时间历程图与相图进行验证,讨论了不同类型的化学突触对神经元特性的影响。之后,在此基础上增加磁通量,建立了具有磁通的耦合ML神经元模型,通过数值仿真探究耦合神经元系统的分岔与同步,探究了时滞对耦合系统分岔与同步的影响,并运用双参数图研究了多个参数改变对分岔及同步的影响。
1. 模型描述与数值模拟
1.1 模型描述
ML神经元模型是描述北极鹅肌肉纤维电活动的一个神经元模型,也是产生动作电位最简单的模型之一。在ML模型中引入化学突触[1],得到如下模型:
$$ \left\{ \begin{aligned} & \dfrac{\text{d}{V}_{1{,}2}}{\text{d}t}=-g{}_{{\rm{Ca}}}m{}_{\infty }({V}_{1{,}2})({V}_{1{,}2}-{V}_{{\rm{Ca}}})-g{}_{{\rm{K}}}w{}_{1{,}2}({V}_{1{,}2}-{V}_{{\rm{K}}})-{g}_{{\rm{l}}}({V}_{1{,}2}-{V}_{{\rm{l}}})-{u}_{1{,}2} +\\& \qquad \dfrac{D({V}_{{\rm{syn}}}-{V}_{1{,}2})}{1 + \mathrm{exp}[-\sigma ({V}_{2{,}1}-\theta )]},\\& \dfrac{\text{d}{w}_{1{,}2}}{\text{d}t}=\lambda ({V}_{1{,}2})({w}_{\infty }({V}_{1{,}2})-{w}_{1{,}2}),\\& \dfrac{\text{d}{u}_{1{,}2}}{\text{d}t}=\mu (0.2 + {V}_{1{,}2}), \end{aligned}\right.$$ (1) 其中
$ {m_\infty },{w_\infty },\lambda \left( V \right) $ 的表达式分别为$$ {m}_{\infty }=\dfrac{1}{2}\left(1 + \mathrm{tanh}\dfrac{V-{v}_{1}}{{v}_{2}}\right),{w}_{\infty }=\dfrac{1}{2}\left(1 + \mathrm{tanh}\dfrac{V-{v}_{3}}{{v}_{4}}\right),\lambda (V)=\dfrac{1}{3}\mathrm{cosh}\left(\dfrac{V-{v}_{3}}{2{v}_{4}}\right), $$ 这里
$ V $ ,$ w $ ,$ u $ 分别表示神经元的膜电位、恢复变量、调节$ V $ 和$ w $ 的慢变量;D表示由化学突触建立耦合关系的耦合强度;$ {V_{{\rm{syn}}}} $ 表示突触反转电压,它依赖于前突触神经元和接受者。耦合是兴奋性的还是抑制性的,依赖于$ {V_{{\rm{syn}}}} $ 的取值,根据文献[2],抑制性条件下,设置$ {V_{{\rm{syn}}}} = - 0.5 $ ,兴奋性条件下,设置$ {V_{{\rm{syn}}}} = 0.3 $ 。突触阈值$ \theta = - 0.35 $ ,比率常数$ \sigma = 5.0 $ ,其余为系统参数,取值为${g_{\rm{l}}} = 0.5$ ,${g_{\rm{K}}} = 2.0$ ,${g_{{\rm{Ca}}}} = 1.2$ ,${V_{{{\rm{l}}}}} = - 0.5$ ,${V_{\rm{K}}} = - 1$ ,${V_{{\rm{Ca}}}} = 1.0$ ,${v_1} = - 0.01$ ,${v_2} = 0.15$ ,${v_3} = 0.1$ ,${v_4} = 0.05$ ,$\mu = 0.005$ 。1.2 数值模拟与结果
为分析耦合神经元系统的同步情况,在此处引入一个统计量[2]——相似函数,其表达式如下:
$$ S(\tau ){\text{ = }}\sqrt {\frac{{\langle {{{({V_{\text{1}}}(t) - {V_2}(t - \tau ))}^2}} \rangle }}{{\sqrt {\langle {V_1^2(t)} \rangle \langle {V_2^2(t)} \rangle } }}}, $$ 这里
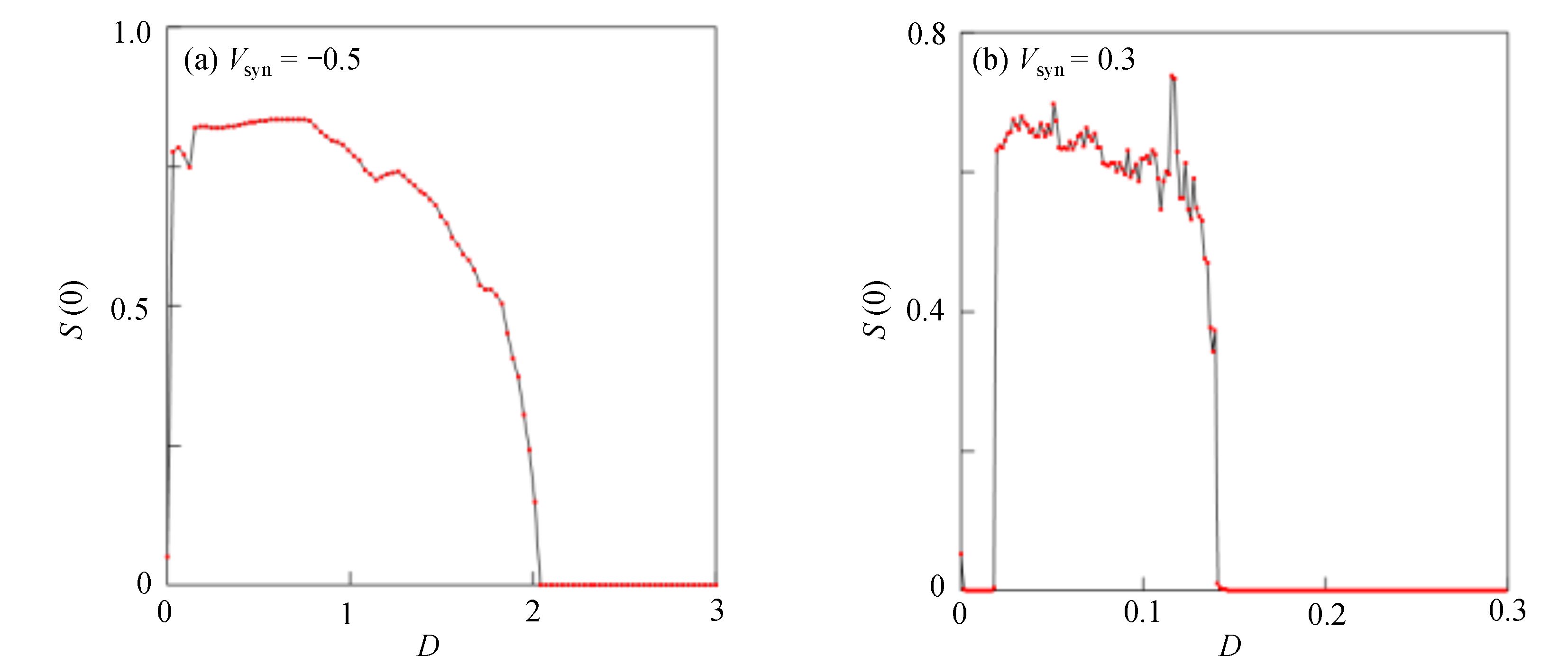
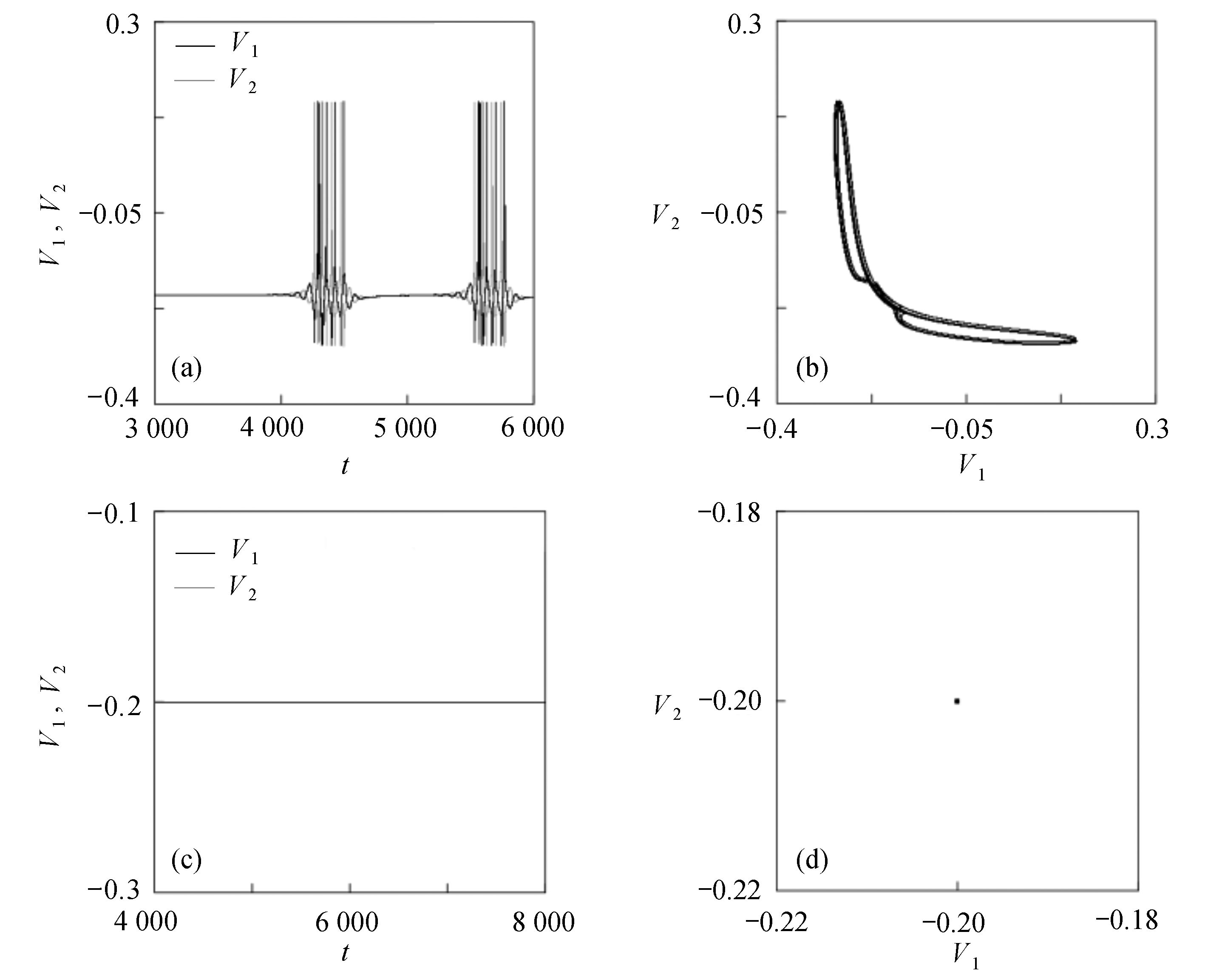
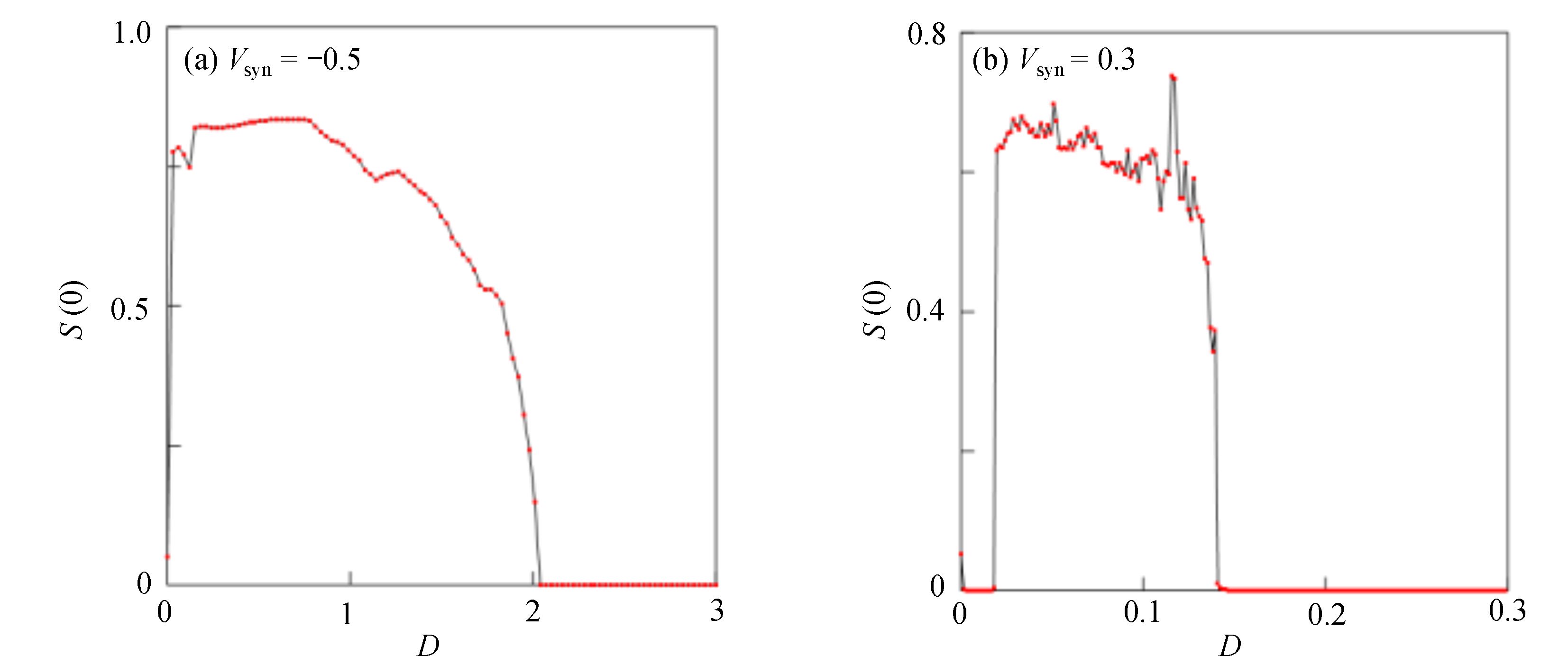
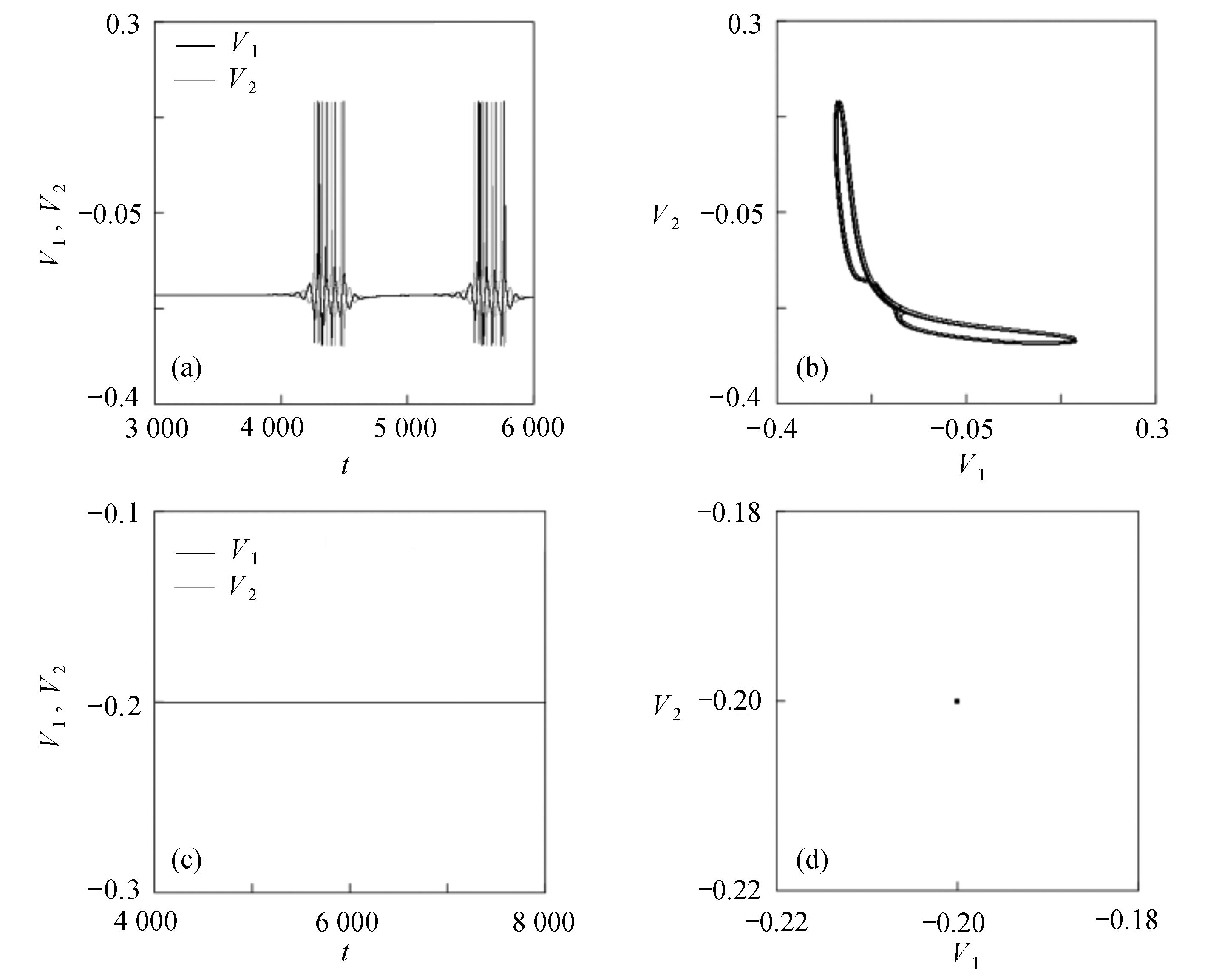
$\langle\; \cdot\;\rangle$ 表示对时间的平均,$ \tau $ 表示时滞,表达式中衡量了两个耦合系统的膜电位${V_1}\left( t \right)$ 和${V_2}\left( t \right)$ 随时间变化时的相关性。当两个神经元之间的放电节律彼此独立时,那么对所有的时滞$ \tau $ ,$S \left( \tau \right) \ne 0$ ;若两个耦合神经元之间的放电模式具有一定的相关性,即存在一个时滞$ \tau $ ,使得$S \left( \tau \right) = 0$ ,那么说明两个神经元之间的放电节律,存在一个时间延迟$ \tau $ 的同步。特别需要指出的是,若两个耦合神经元系统的放电状态是完全同步的,则存在$ \tau = 0 $ ,使$S \left( \tau \right) = 0$ ,即$S \left( 0 \right) = 0$ ,即耦合系统达到完全同步状态。相应地,若相似函数值越小,则表明耦合系统越相关,即同步度越高[13]。对化学突触的ML神经元模型,其抑制性与兴奋性条件下的相似函数图如图1所示,图1(a)反映了抑制性条件下相似函数值S(0)与耦合强度D的关系,可以发现耦合系统在耦合强度D=2.04时达到同步。图1(b)反映了兴奋性条件下相似函数值S(0)与耦合强度D的关系,发现系统在耦合强度D=0.006时同步,但并不稳定,耦合强度继续变大,耦合系统不再同步。直到耦合强度D=0.175时,耦合系统达到同步,并趋于稳定。图2与图3是进一步对相似函数变化图的验证,反映了耦合系统随时间尺度的增大,耦合系统放电的状态和同步的情况。抑制性条件下的时间历程图与相图如图2所示。取耦合强度D=1.98,S(0)=0.239。其时间历程图与相图如图2(a)、图2(b)所示。图2(a)中黑色表示第一个神经元的放电节律,红色为第二个神经元的放电节律,两个神经元放电开始为静息态,之后随时间的增加,两个神经元开始放电,但两个神经元的放电节律存在错位,表示两个神经元之间不同步。图2(b)中的相图也说明两个神经元之间不同步。取耦合强度D=2.04 ,S(0)=0。其时间历程图与相图如图2(c)、图2(d)所示。图2(c)中时间历程图呈现为一条水平直线,两个神经元都处于静息状态,为静息同步。图2(d)中,相图在
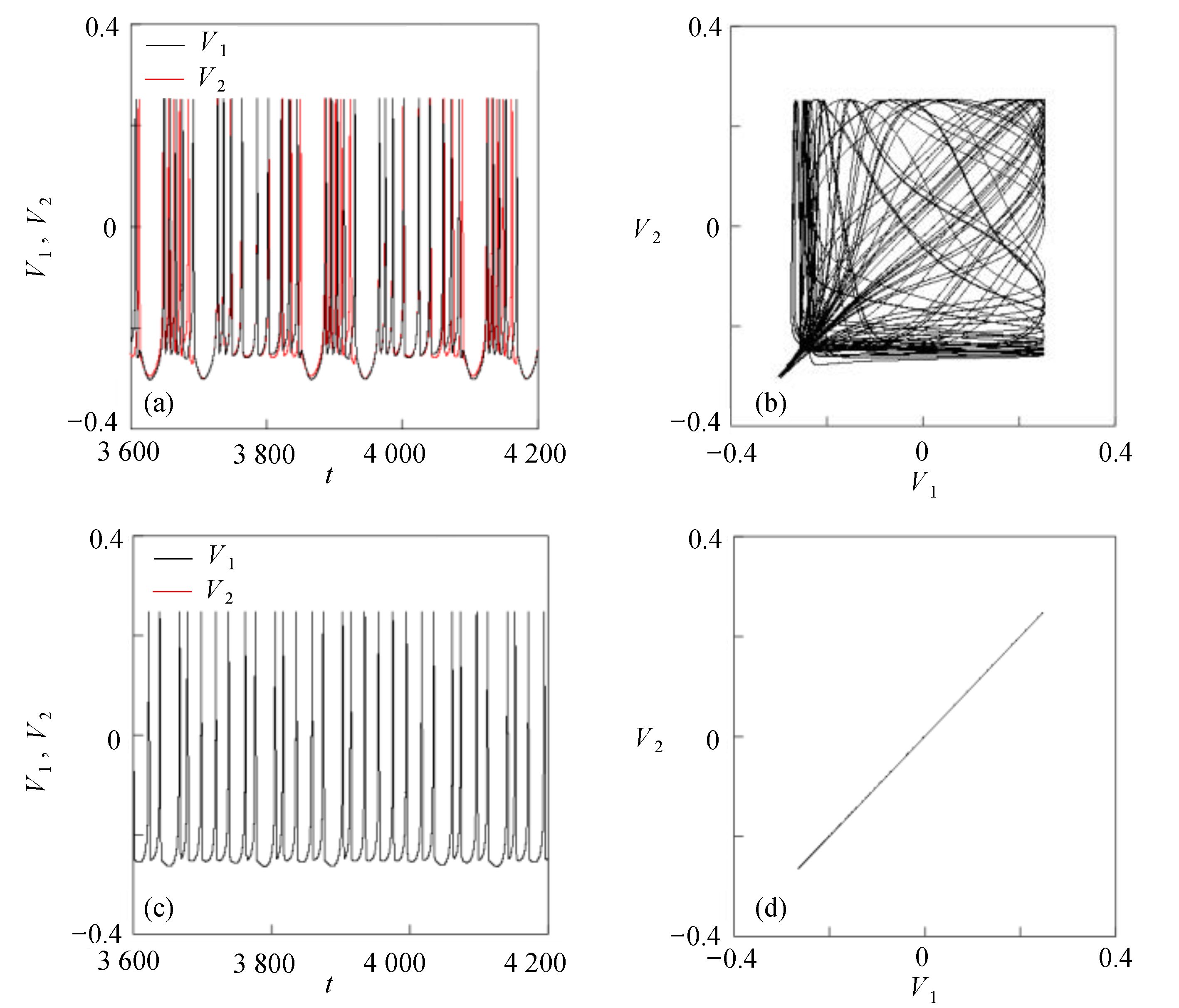
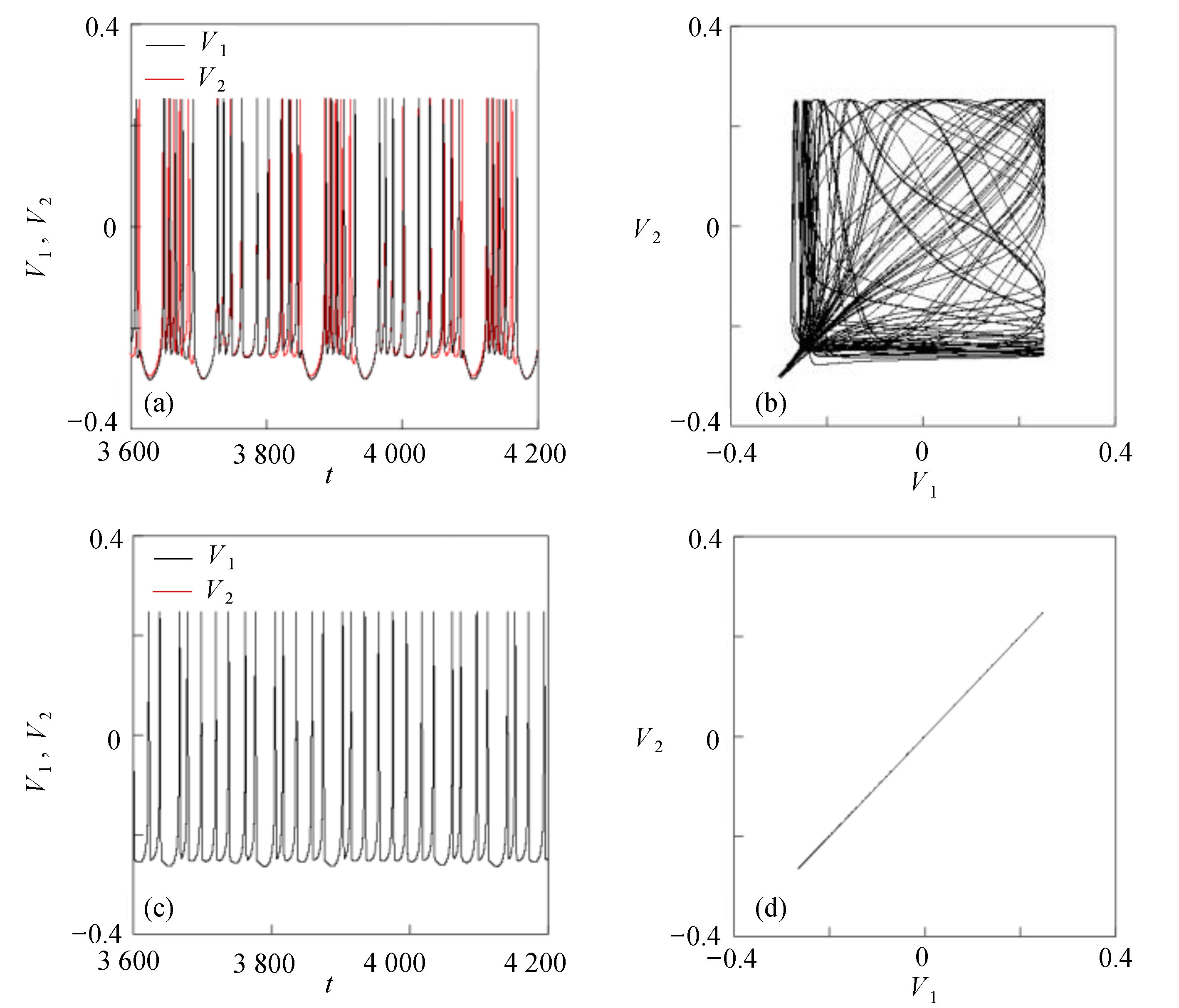
$\left( {{V_1},{V_2}} \right)$ 平面内呈现一个点,也说明耦合系统处于静息同步。兴奋性条件下的相图与时间历程图如图3所示。取耦合强度D=0.081, S(0)=0.585639。其时间历程图与相图如图3(a)、图3(b)所示,两个神经元的簇放电同时发生,但两个神经元的放电节律存在一定的错位,表示两个神经元之间不同步。图3(b)中的相图也表明两个神经元是不相关的。取耦合强度D=0.175 ,S(0)=0,时间历程图如图3(c)、图3(d)所示,此时两个神经元都为峰放电状态,并且放电节律一致,表示耦合系统达到同步。图3(d)中的相图在$\left( {{V_1},{V_2}} \right)$ 平面内呈现一条斜率为1的直线,表示此时耦合系统达到同步。 图 2 系统(1)在抑制性条件下的时间历程图与相图:(a)
图 2 系统(1)在抑制性条件下的时间历程图与相图:(a)$D = 1.98$ 时的时间历程图;(b)$D = 1.98$ 时的相图;(c)$D = 2.04$ 时的时间历程图;(d)$D = 2.04$ 时的相图Figure 2. Time history diagrams and phase diagrams of system (1) under inhibition: (a) the time history diagram at time$D = 1.98$ ; (b) the phase diagram at time$D = 1.98$ ; (c) the time history diagram at time$D = 2.04$ ; (d) the phase diagram at time$D = 2.04$  图 3 系统(1)在兴奋性条件下的时间历程图与相图:(a)
图 3 系统(1)在兴奋性条件下的时间历程图与相图:(a)$D = 0.081$ 时的时间历程图;(b)$D = 0.081$ 时的相图;(c)$D = 0.175$ 时的时间历程图;(d)$D = 0.175$ 时的相图Figure 3. Time history diagrams and phase diagrams of system (1) under excitatory condition: (a) the time history diagram at time$D = 0.081$ ; (b) the phase diagram at time$D = 0.081$ ; (c) the time history diagram at time$D = 0.175$ ; (d) the phase diagram at time$D = 0.175$ 通过对抑制性化学突触和兴奋性化学突触对耦合系统同步影响的分析,发现在抑制性条件下,耦合系统随着耦合强度的变大,神经元放电的时间段逐渐减小,处于静息的时间段不断增加,在耦合强度增大到一定程度时,耦合系统为静息状态,达到静息同步。兴奋性条件下的耦合神经元与抑制性条件下的耦合神经元的不同之处为在耦合系统达到同步之后,神经元依然处于放电状态。说明兴奋性的化学突触能够刺激耦合系统在达到同步之后依然放电。
2. 时滞对神经元分岔的影响
2.1 模型描述
神经元内外磁场变化会引起电磁感应现象[3-5],对神经元放电会产生影响,在具有化学突触的模型中引入磁通变量和时滞[9],得到如下模型:
$$ \left\{\begin{array}{l}\dfrac{\text{d}{V}_{1,2}}{\text{d}t}=-g{}_{{\rm{Ca}}}m{}_{\infty }({V}_{1,2})({V}_{1,2}-{V}_{{\rm{Ca}}})-g{}_{{\rm{K}}}w{}_{1,2}({V}_{1,2}-{V}_{{\rm{K}}})-{g}_{{\rm{l}}}({V}_{1,2}-{V}_{{\rm{l}}})-{u}_{1,2}\text{ + }I-{k}_{1}\rho ({\varphi }_{1,2}){V}_{1,2}+\\ \qquad \dfrac{D({V}_{{\rm{syn}}}-{V}_{1,2})}{1 + \mathrm{exp}\{-\sigma [{V}_{2,1}(t-{\tau }_{\text{1},\text{2}})-\theta ]\}},\\ \dfrac{\text{d}{w}_{1,2}}{\text{d}t}=\lambda ({V}_{1,2})({w}_{\infty }({V}_{1,2})-{w}_{1,2}),\text{ }\\ \dfrac{{\text{d}}u_{1,2}}{\text{d}t}=\mu (0.2 + {V}_{1,2}),\\ \dfrac{{\rm{d}}{\varphi }_{1,2}}{{\rm{d}}t}={V}_{1,2}-{k}_{2}{\varphi }_{1,2}-{D}_{1}({\varphi }_{2}-{\varphi }_{1}),\end{array} \right.$$ (2) 其中
$$ \rho (\varphi ) = (\alpha + 3\beta {\varphi ^2}) , {m_\infty } = \dfrac{1}{2}\left(1 + \tanh \dfrac{{V - {v_1}}}{{{v_2}}}\right), {w_\infty } = \dfrac{1}{2}\left(1 + \tanh \dfrac{{V - {v_3}}}{{{v_4}}}\right) , \lambda (V) = \dfrac{1}{3}\cosh \left(\dfrac{{V - {v_3}}}{{2{v_4}}}\right),$$ 这里
$ V $ ,$ w $ ,$ u $ 等其余基本参数与上文含义相同;$\varphi $ 表示穿过神经元细胞膜的磁通量;I表示外界电流刺激;$ {k_1},{k_2} $ 被称为膜电位与磁通量之间的相互作用关系,也称为反馈增益;$ \tau $ 表示时滞;D表示化学耦合强度,D1表示磁通耦合强度;$\alpha $ 和$\beta $ 都是固定参数;$\alpha = 0.1$ ,$\beta = 0.2$ ,${k_1} = - 0.5$ ,${k_2} = 2.0$ ,$ I = 1.0 $ ,$ {D_1} = 0.075 $ 。2.2 分岔分析
2.2.1 单参数分岔分析
在数值计算中,采用四阶变步长Runge-Kutta方法对考虑时滞的带有磁通和化学突触的耦合神经元系统进行分岔分析,研究时滞对其动力学行为的影响。主要通过两方面动力学特性进行探讨,首先是通过峰-峰间期(ISI)分岔图探讨耦合神经元系统的分岔情况,其中峰-峰间期表示神经元膜电位达到相邻两次动作电位的时间差,通过时间差描述神经元的放电规律。之后是通过相似函数探讨耦合神经元中两个神经元的同步情况。在以下分析中,在分析分岔时,以第一个神经元进行分岔分析,但因为在进行分岔分析时所选取的初值是一样的,两个神经元的分岔是同步进行的,所以分岔的结论对第二个神经元同样适用。
选取磁通[3]反馈增益
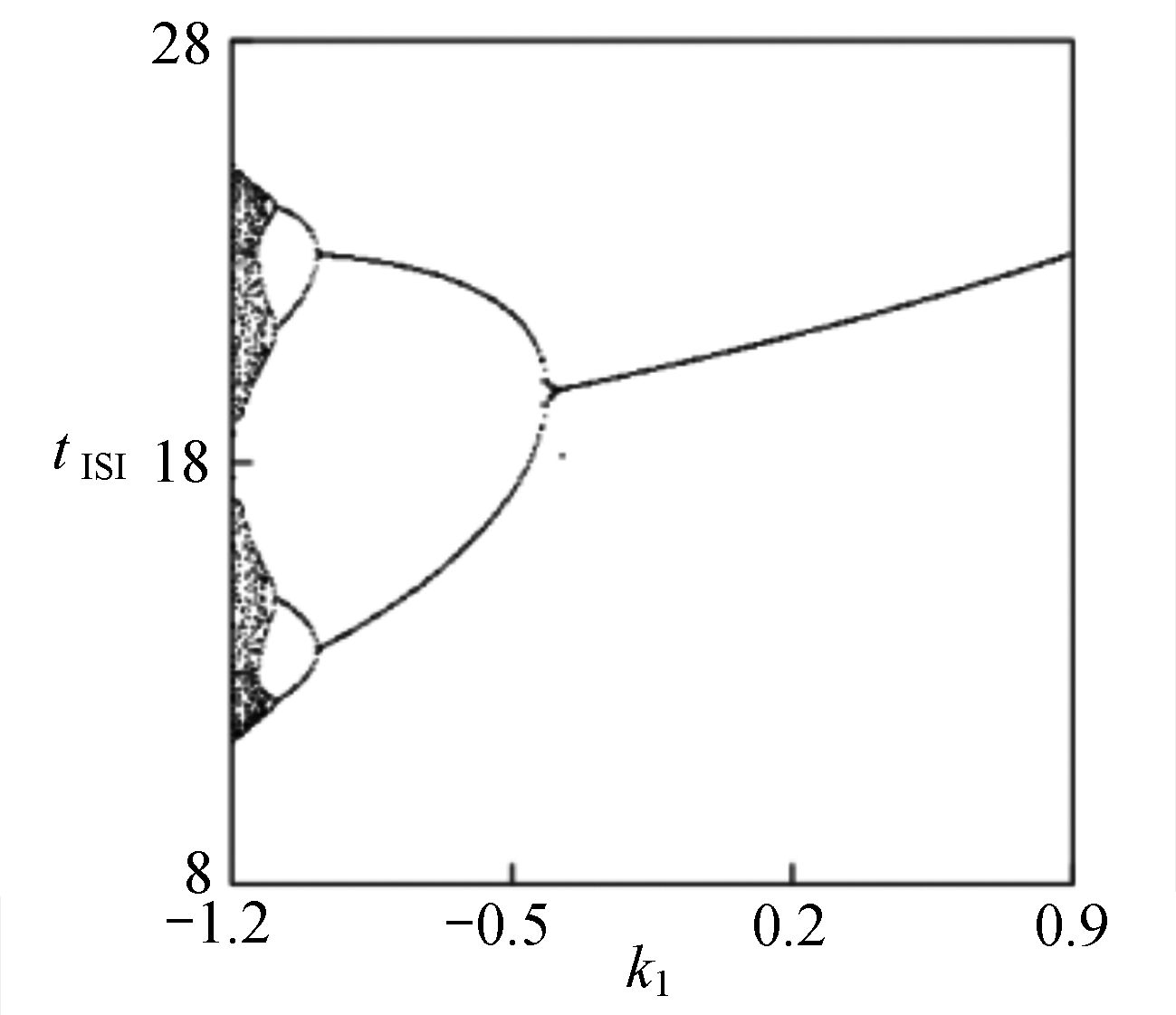
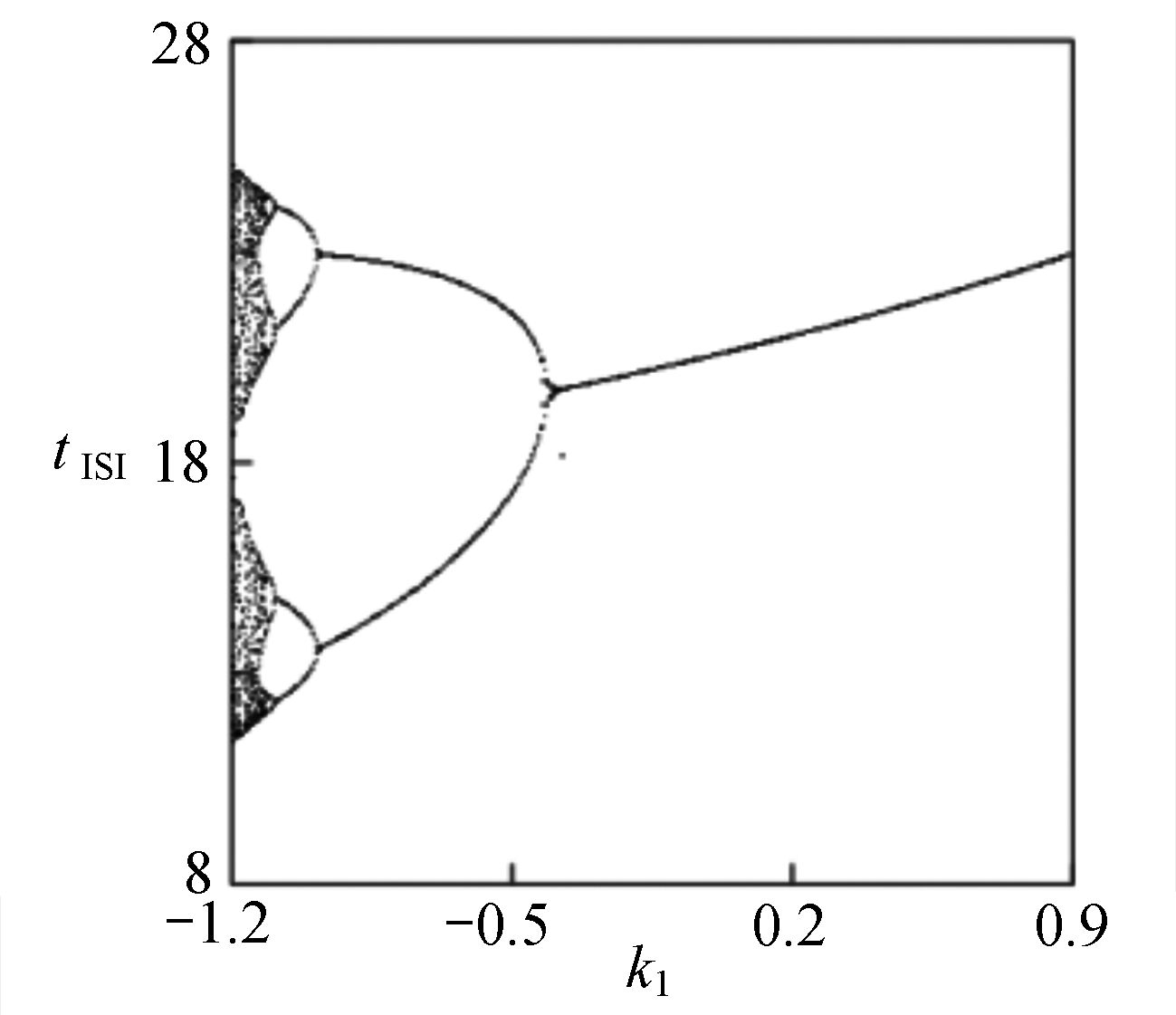
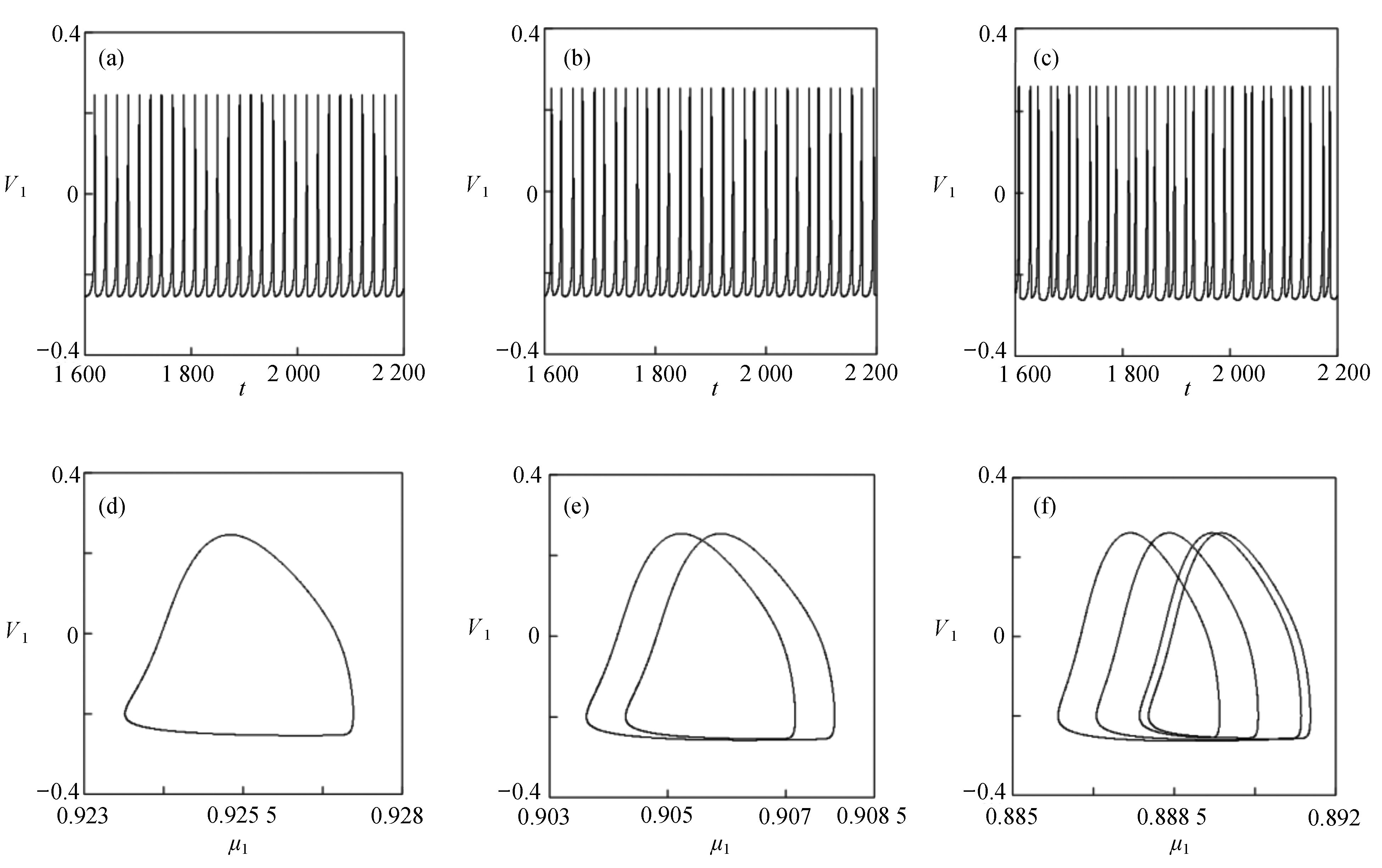
$ {k_1} $ 进行数值仿真,峰-峰间期分岔图如图4所示,随着反馈增益的不断增大,耦合系统呈现逆倍周期分岔。当$ - 1.2 \leqslant {k_1} \leqslant - 1.137$ 时,耦合系统处于混沌状态,随着反馈增益的不断增大,至${k_1} = - 1.137$ ,耦合系统呈现周期8放电,至$ {k_1} = - 1.116 $ ,退化至周期4放电,至$ {k_1} = - 0.993 $ ,退化至周期2放电,最后至${k_1} = - 0.419\;5$ ,退化至周期1放电。接下来对反馈增益$ {k_1} $ 的峰-峰间期分岔图进行验证,分别取${k_1} = 0.2,-0.5, -1.08$ ,得到对应的时间历程图与相图,如图5所示。从图5中可以看到${k_1} = 0.2$ 时,耦合系统呈现周期1放电;${k_1} = - 0.5$ 时,耦合系统呈现周期2放电;${k_1} = - 1.08$ 时,耦合系统呈现周期4放电。通过上述分析,说明耦合系统在反馈增益$ {k_1} $ 的影响下会产生丰富的放电行为。 图 5 系统(2)在不同反馈增益下的时间历程图与相图:(a)
图 5 系统(2)在不同反馈增益下的时间历程图与相图:(a)$ {k_1} = 0.2 $ 的时间历程图;(b)$ {k_1} = - 0.5 $ 的时间历程图;(c)$ {k_1} = - 1.08 $ 的时间历程图;(d)$ {k_1} = 0.2 $ 的相图;(e)$ {k_1} = - 0.5 $ 的相图;(f)$ {k_1} = - 1.08 $ 的相图Figure 5. Time history diagrams and phase diagrams of system (2) under different feedback gains: (a) the time history diagram at time$ {k_1} = 0.2 $ ; (b) the time history diagram at time$ {k_1} = - 0.5 $ ; (c) the time history diagram at time$ {k_1} = - 1.08 $ ; (d) the phase diagram at time$ {k_1} = 0.2 $ ; (e) the phase diagram at time$ {k_1} = - 0.5 $ ; (f) the phase diagram at time$ {k_1} = - 1.08 $ 在反馈增益
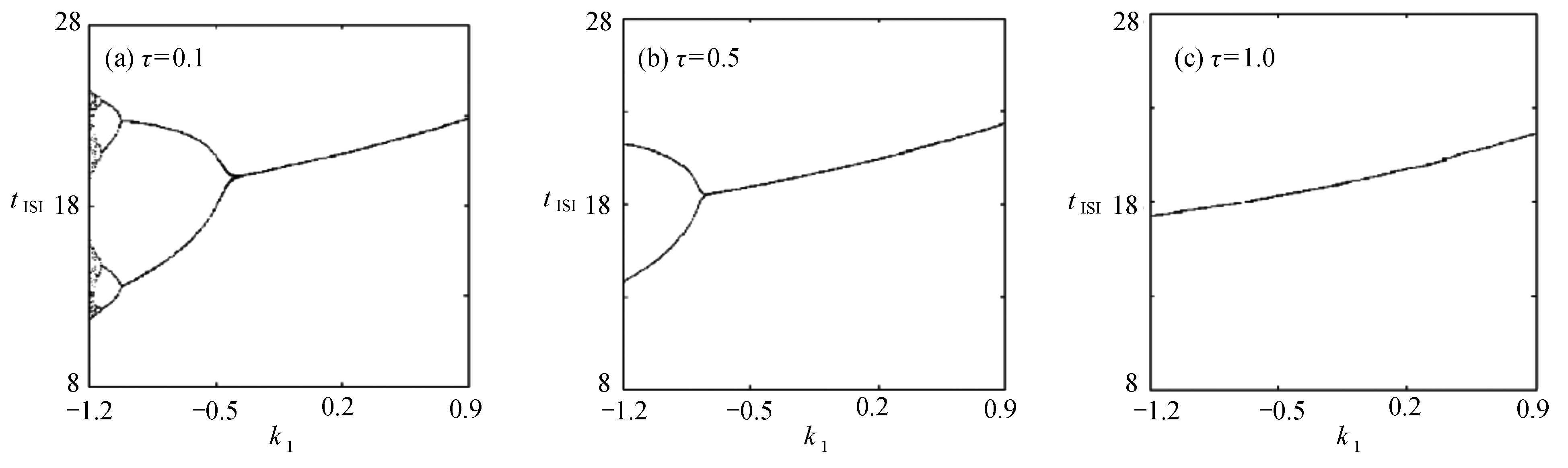
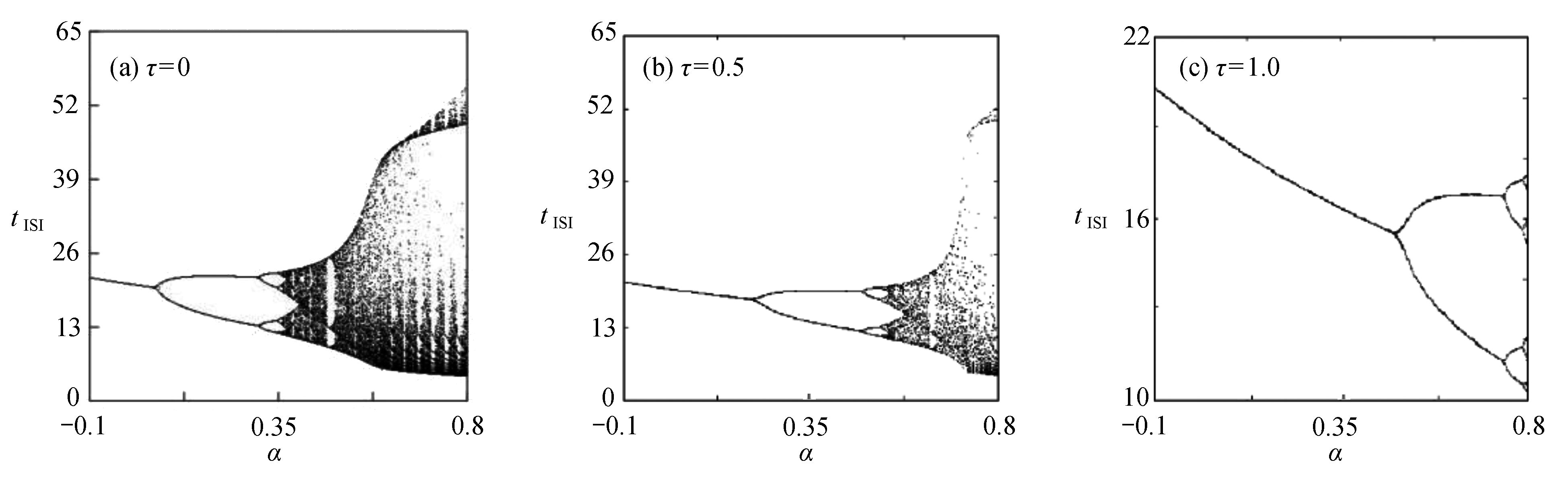
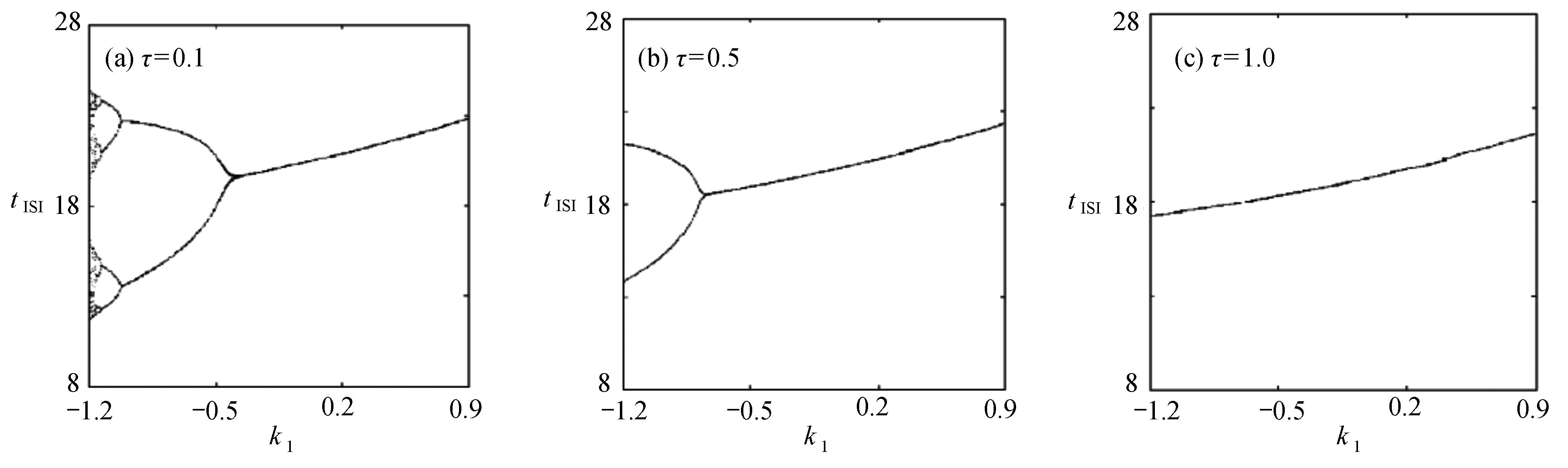
$ {k_1} $ 的影响下,耦合系统产生了丰富的放电行为,所以引入不同的时滞[10],观察时滞对反馈增益$ {k_1} $ 分岔图的影响,如图6所示,当时滞$ \tau = 0.1 $ 时,与图4进行对比,耦合系统仍呈现逆倍周期分岔,随反馈增益$ {k_1} $ 的不断增大,耦合系统仍从混沌放电到周期8放电,再到周期4放电,再到周期2放电,之后到周期1放电,但混沌放电区间明显减少,周期放电区间增加。当时滞$ \tau = 0.5 $ 时,耦合系统直接从周期2退化至周期1。当时滞$ \tau = 1.0 $ 时,耦合系统只呈现周期1放电。接下来对参数
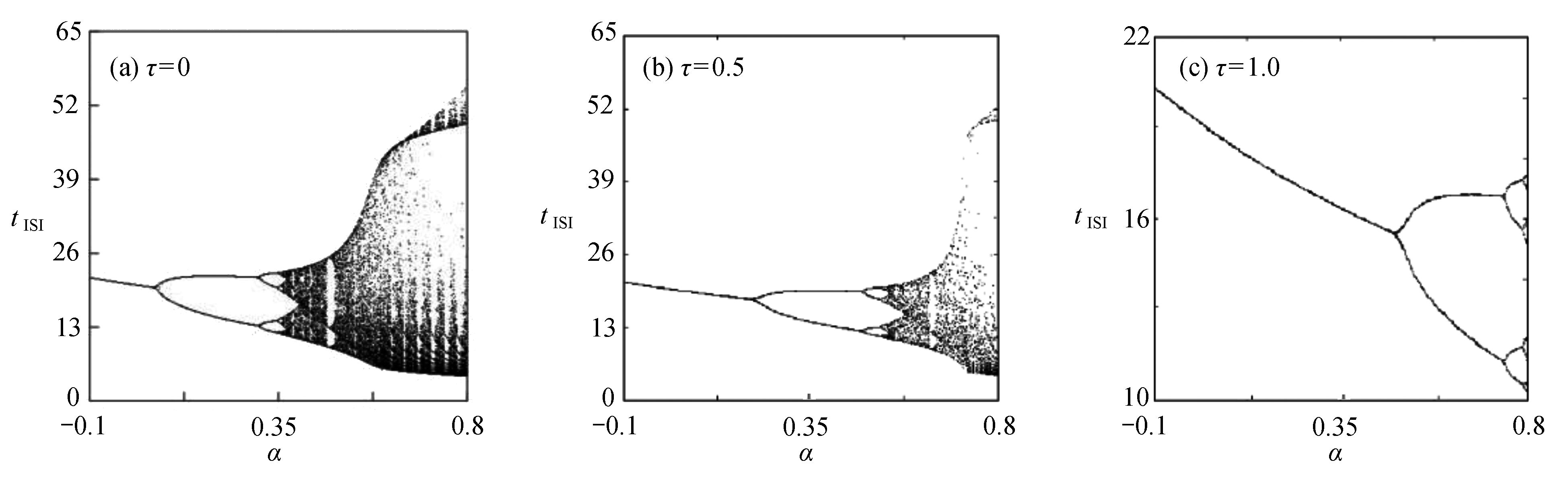
$\alpha $ 的峰-峰间期分岔图进行分析,不同时滞滞[11]下参数$ \alpha $ 的峰-峰间期分岔图如图7所示。当时滞$ \tau = 0 $ 时,随参数$\alpha $ 的变化,耦合系统首先经历倍周期分岔,之后进入混沌放电。从周期1放电倍化至周期2放电再到周期4放电,之后进入混沌放电,经过混沌放电之后,又进入短暂的周期3放电,之后进入混沌放电。当时滞$ \tau = 0.5 $ 时,与图7(a)对比,发现耦合系统仍经历倍周期分岔,之后进入混沌放电,但混沌放电区间明显减少。当时滞$ \tau = 1.0 $ 时,耦合系统只出现倍周期分岔,不再出现混沌放电现象。通过对添加时滞的反馈增益
${k_1}$ 分岔图及参数$\alpha $ 的分岔图的分析,发现引入时滞之后,耦合系统放电的混沌现象减少,并随时滞增大,混沌现象减少越多,甚至消失。说明时滞增强了耦合系统放电的周期性,可以通过引入有效的时滞的方法,来实现对耦合系统放电行为的分岔和混沌控制。2.2.2 双参数分岔分析
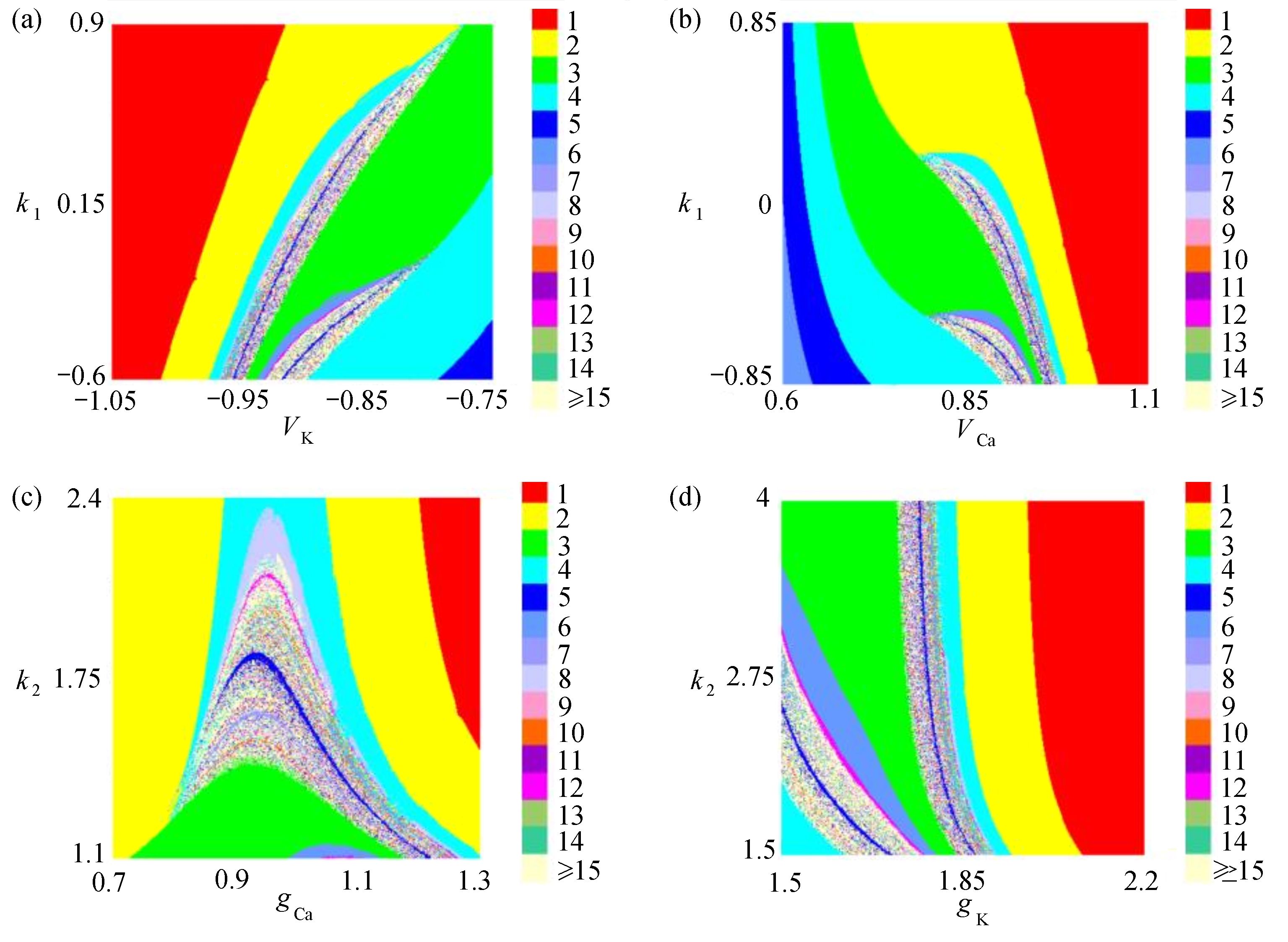
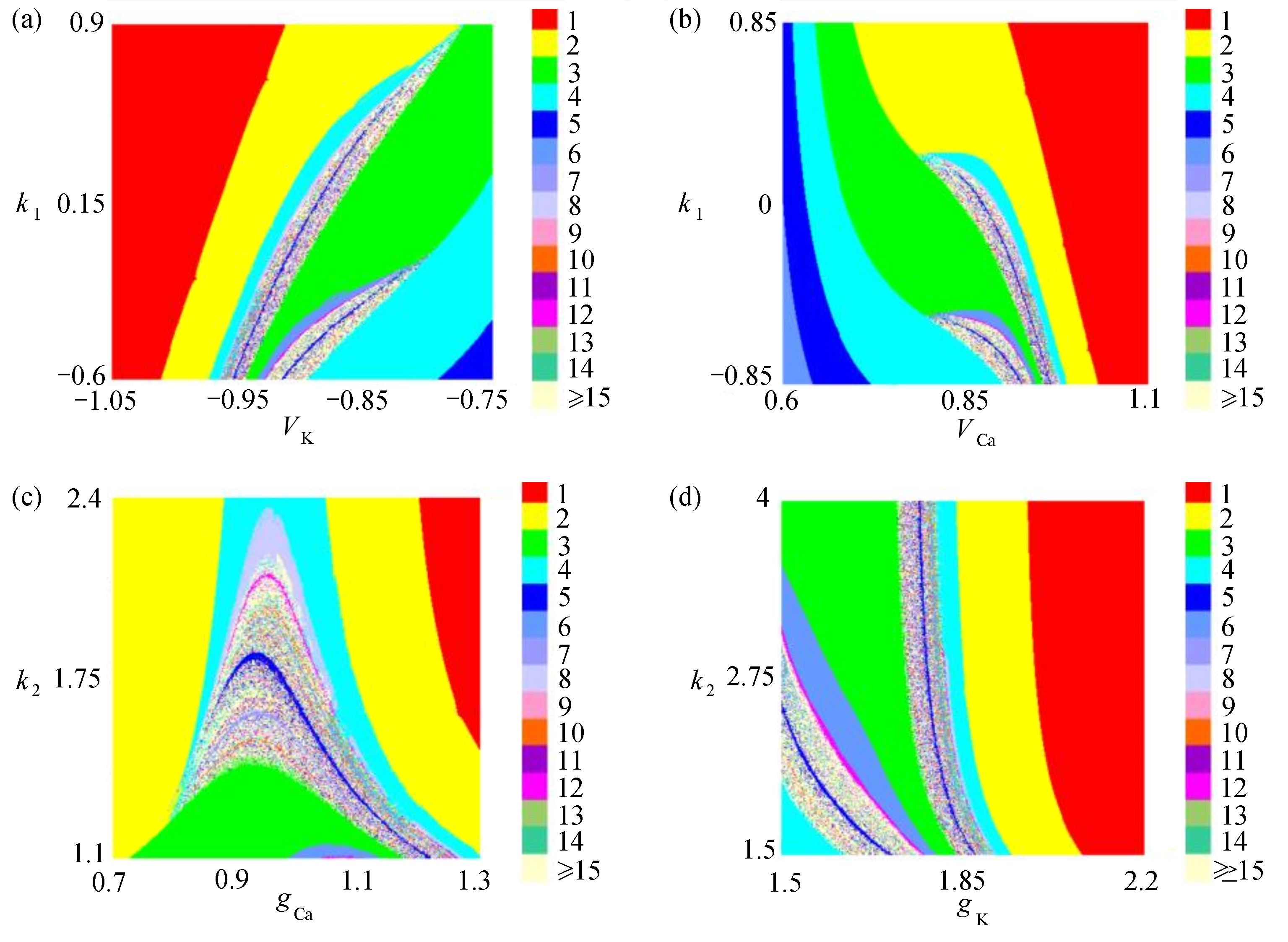
为了进一步研究多个参数对耦合神经元系统放电模式的影响,运用双参数分岔图进行分析。选取反馈增益
$ {k_1} $ 与参数$V_{\rm{K}}$ ,$V_{\rm{Ca}}$ ,以及反馈增益$ {k_2} $ 与参数$g_{\rm{Ca}}$ ,$g_{\rm{K}}$ 进行数值模拟,如图8所示。图中红色表示周期1放电,黄色表示周期2放电,绿色表示周期3放电,蓝绿色表示周期4放电等,每个颜色都代表一个周期,代表的周期数由图右边的图标给出,其中大于等于周期15的由浅黄色给出。观察图8(a),发现在$({k_1},V_{\rm{K}})$ 平面内,固定$ {k_1} = - 0.225 $ 进行分析,整个耦合系统的分岔从左边开始,首先为红色区域呈现周期1放电,随着参数$V_{\rm{K}}$ 的增加,耦合系统发生三次倍周期分岔,进入黄色区域周期2放电、蓝绿色区域周期4放电及非常狭小的浅灰蓝色区域周期8放电,之后进入混沌放电,经过混沌放电之后,又一次重复发生倍周期分岔,进入绿色区域周期3放电、淡蓝色区域周期6放电及品红色区域周期12放电,之后又一次进入混沌放电,紧接着发生加周期分岔,进入蓝绿色区域周期4放电及蓝色区域周期5放电。观察图8(b),发现在$({k_1},V_{\rm{Ca}})$ 平面内,固定$ {k_1} = - 0.8 $ 进行分析,整个耦合系统的分岔从右边开始,首先为红色区域周期1放电,随着参数$V_{\rm{Ca}}$ 的不断减小,耦合系统通过三次倍周期分岔进入黄色区域周期2放电、蓝绿色区域周期4放电及非常狭小的浅灰蓝色区域周期8放电,之后进入混沌放电,通过混沌放电,耦合系统重复发生倍周期分岔,进入绿色区域周期3放电及淡蓝色区域周期6放电,随参数$V_{\rm{Ca}}$ 继续减小,又进入混沌放电,通过第二次混沌放电后,耦合系统开始进入加周期分岔,依次进入周期4、周期5、周期6放电。观察图8(c),发现在$ ({k_2},g_{\rm{Ca}}) $ 平面内,耦合系统整体分岔呈现山峰状,固定$ g_{\rm{Ca}} = 1 $ 进行分析,首先耦合系统整体从右上角开始呈现红色区域周期1放电,之后从两边向中间,通过多次倍周期分岔,依次出现周期2放电、周期4放电、周期8放电,之后随着反馈增益$ {k_2} $ 减小,混沌放电与周期放电交替出现,但周期放电区域非常小,之后随反馈增益$ {k_2} $ 继续减小,继续发生倍周期分岔,出现周期3放电、周期6放电及小范围周期12放电。观察图8(d),发现在$ ({k_2},g_{\rm{K}}) $ 平面内,固定$ {k_2} = 1.6 $ 进行分析,整个耦合系统的分岔从右边开始,首先为周期1放电,之后随参数$ g_{\rm{K}} $ 不断减小,耦合系统发生两次倍周期分岔,进入周期2、周期4放电,之后进入混沌放电,之后进入周期3放电,通过倍化分岔后,进入周期6与周期12放电,之后又进入混沌放电,通过混沌放电又进入周期4放电。 图 8 反馈增益
图 8 反馈增益$ {k_1} $ ,$ {k_2} $ 与不同参数的双参数分岔图:(a)$ {k_1} $ 与$V_{\rm{K}}$ 双参数分岔图;(b)$ {k_1} $ 与$ V_{\rm Ca} $ 双参数分岔图;(c)$ {k_2} $ 与$ g_{\rm Ca} $ 双参数分岔图;(d)$ {k_2} $ 与$ g_{\rm{K}} $ 双参数分岔图Figure 8. Two-parameter bifurcation diagrams with feedback gains and different parameters: (a) the$ {k_1} $ and$ V_{\rm{K}} $ two-parameter bifurcation diagram; (b) the$ {k_1} $ and$ V_{\rm Ca} $ two-parameter bifurcation diagram; (c) the$ {k_2} $ and$ g_{\rm Ca} $ two-parameter bifurcation diagram; (d) the$ {k_2} $ and$ g_{\rm{K}} $ two-parameter bifurcation diagram3. 时滞对耦合神经元同步的影响
3.1 单参数分析
为研究耦合系统(2)的同步行为,仍利用上文中的相似函数,运用四阶变步长Runge-Kutta方法进行数值模拟。
以化学耦合强度D为参数,分别得到耦合强度D在
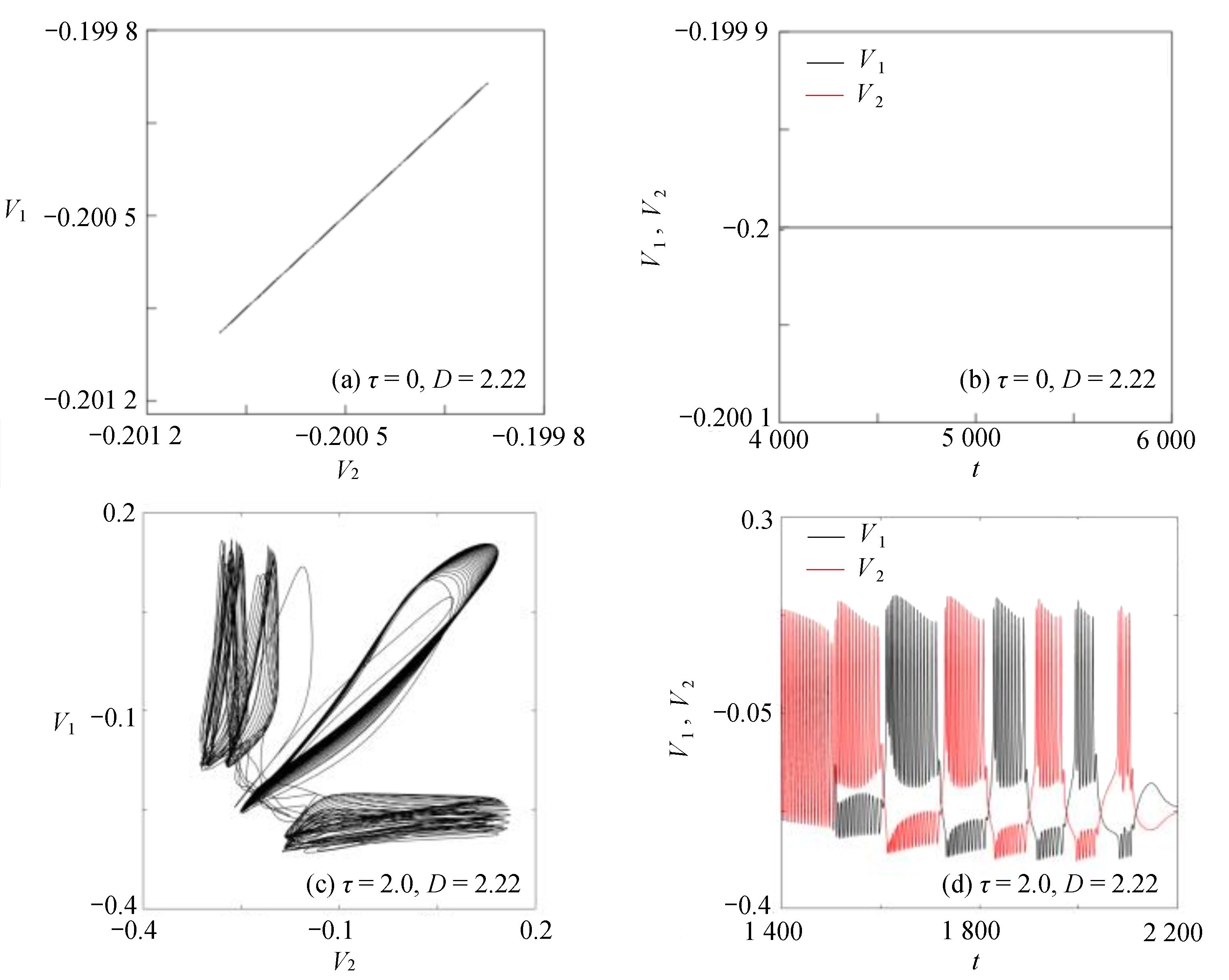
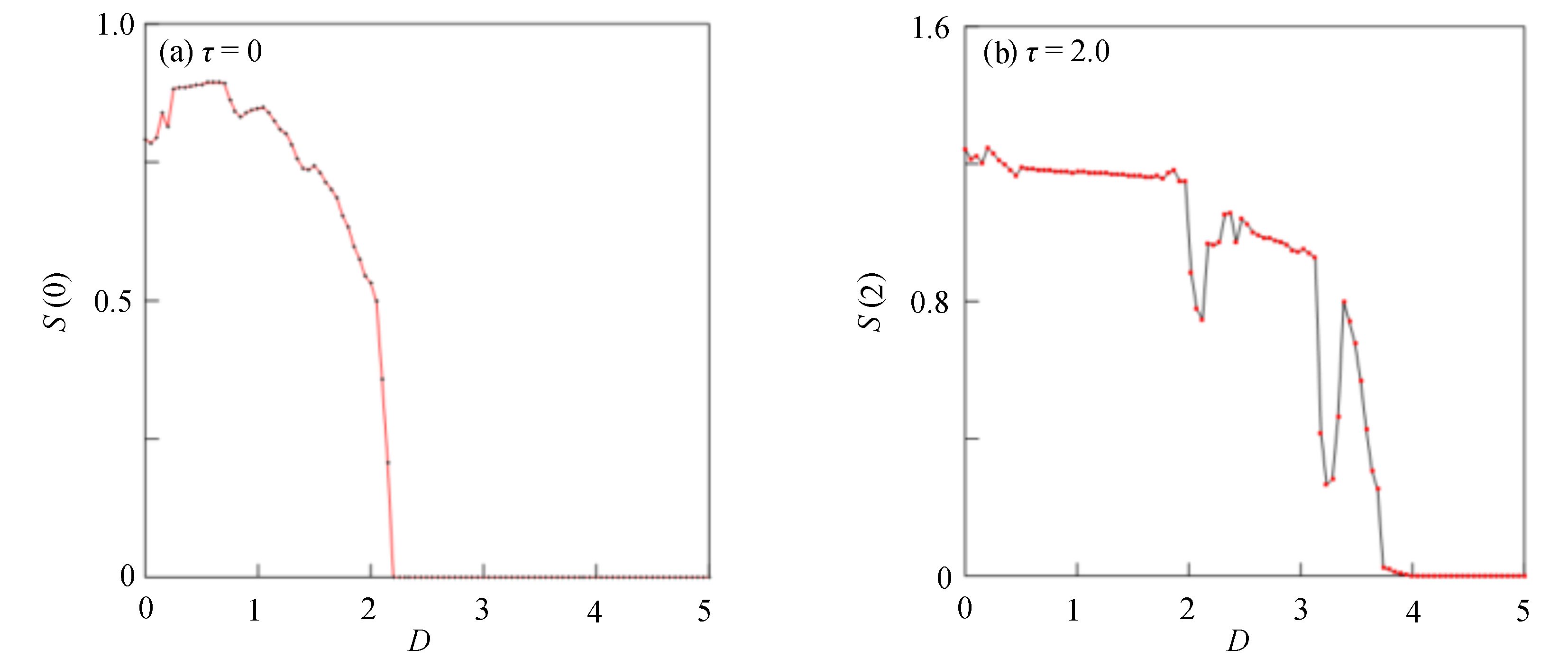
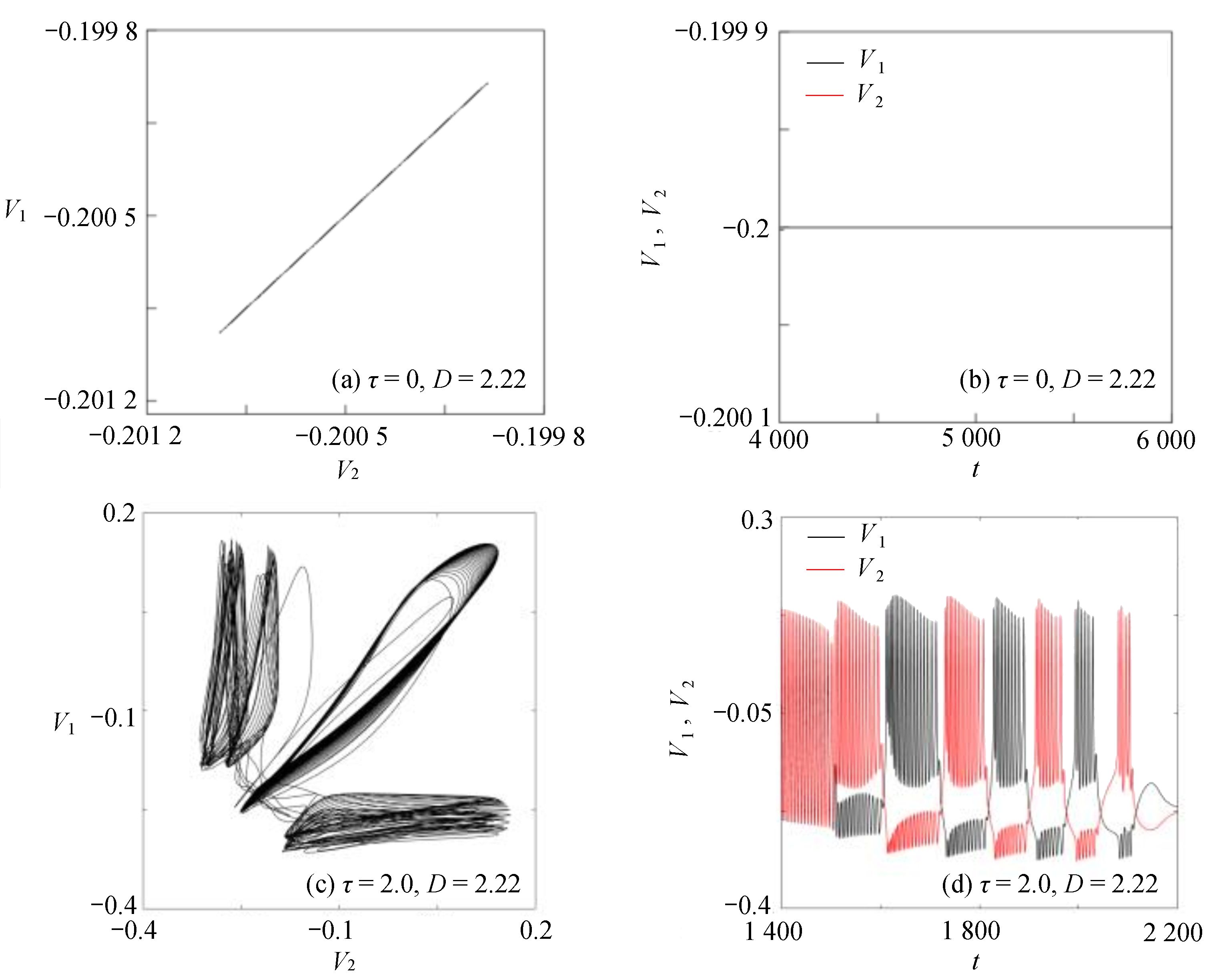
$ \tau = 0 $ 和$ \tau = 2.0 $ 等时滞作用下的相似函数图[12,14-16],如图9所示,观察图9(a),发现耦合系统在$ \tau = 0 $ ,耦合强度D<1时,相似函数的值约等于0.75,此时相似函数值比较大,耦合系统中的两个神经元相关性较小,耦合系统未达到同步。随着耦合强度不断增加,相似函数值不断减小,说明耦合系统中两个神经元之间的相关性不断增加,耦合强度在2.2时,相似函数值急剧减小至0,说明耦合系统中两个神经元之间的相关性非常大,耦合系统达到同步。观察图9(b),发现耦合系统在$ \tau = 2.0 $ ,耦合强度D<2时,相似函数值约等于1.2,此时相似函数值比较大,耦合系统中的两个神经元相关性较小,耦合系统未达到同步。耦合系统在耦合强度D=2与D=3附近出现了两次大幅度的波动,但相似函数值未达到0,在耦合强度大于3之后,相似函数值逐渐减小,在耦合强度达到3.8时,相似函数值等于0,说明耦合系统中两个神经元之间的相关性非常大,耦合系统达到同步。接下来选取耦合强度D=2.2,在$ \tau = 0 $ 与$ \tau = 2.0 $ 处的相图与时间历程图对以上分析加以验证,如图10所示。图10(a)、图10(b)为时滞$ \tau = 0 $ 时的相图与时间历程图,相图呈现一条斜率为1的直线,说明此时耦合系统达到同步,时间历程图呈现一条水平的直线,说明此时耦合系统处于一种静息同步状态。图10(c)、图10(d)为时滞$ \tau = 2.0 $ 处的相图与时间历程图,相图不是斜率为1的直线,说明此时耦合系统未达到同步,时间历程图中两个神经元的放电也有错位,进一步验证了此时神经元未达到同步。通过以上分析,对比在时滞
$ \tau = 0 $ 与$ \tau = 2.0 $ 时的相似函数图,发现在具有化学突触耦合与磁通耦合的神经元系统中,添加时滞后,使耦合系统在原本的同步状态变为非同步状态,即时滞的添加会破坏耦合系统的同步。3.2 双参数分析
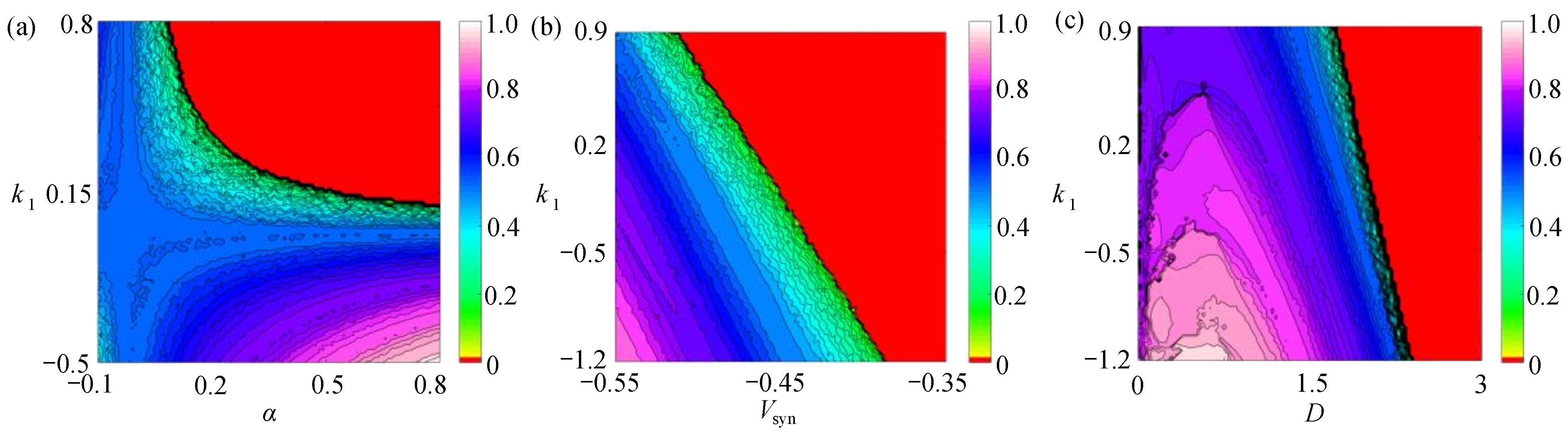
为了进一步分析多个参数对耦合系统同步行为的影响,在无时滞状态下,通过相似函数进行数值模拟,分别得到反馈增益
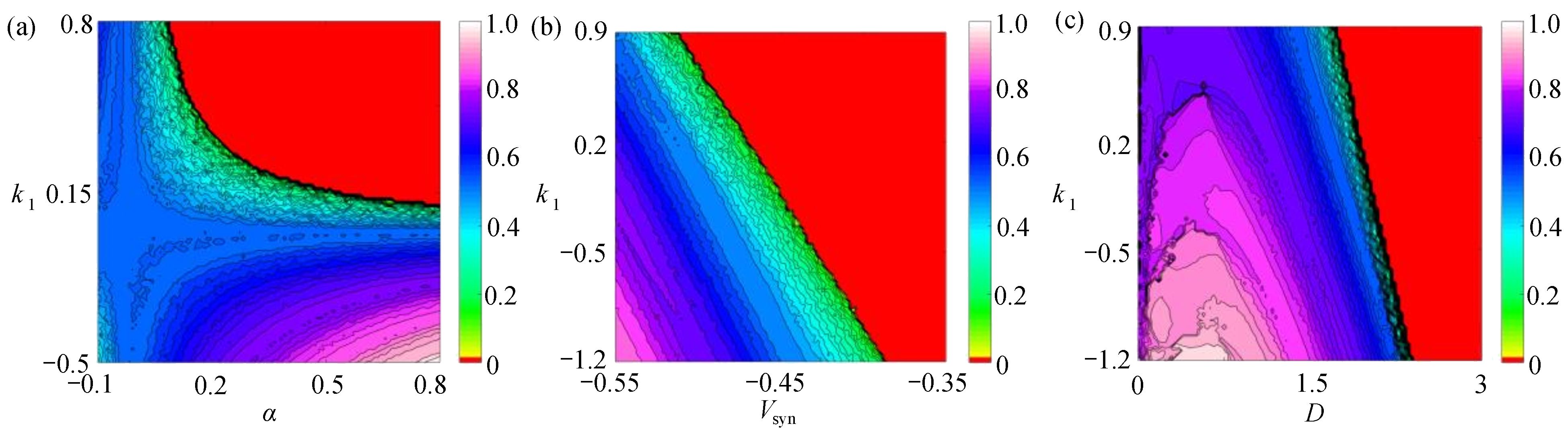
${k_1}$ 与参数$\alpha $ ,${V_{{\rm{syn}}}}$ 和耦合强度的相似函数图,如图11所示。红色区域表示耦合系统同步区域,其他颜色区域表示耦合系统不同步区域。观察图11(a),发现在$ ({k_1},\alpha ) $ 平面内,在区间$ {k_1} \in \left[ { - 0.5,0.8} \right] $ 内,$ \alpha < 0.093\;5 $ 时,耦合系统始终处于蓝色及蓝绿色区域,说明耦合系统没有达到同步;在$ \alpha = 0.093\;5 $ ,$ {k_1} = 0.8 $ 时,S(0)= 0.000001,此时耦合系统进入红色区域,达到同步,之后随参数$ \alpha $ 不断增加,红色区域逐渐变大,蓝色及蓝绿色区域逐渐变小,说明耦合神经元之间同步的范围越来越多。观察图11(b),发现在$({k_1},{V_{{\rm{syn}}}})$ 平面内,在区间$ {k_1} \in \left[ { - 1.2,0.9} \right] $ 内,${V_{{\rm{syn}}}} < - 0.503$ 时,耦合系统始终处于红色区域、蓝色区域及蓝绿色区域,相似函数值逐渐减小,但没有达到0,说明耦合系统没有达到同步,在${V_{{\rm{syn}}}} = - 0.503$ ,$ {k_1} = 0.9 $ 时,S(0)= 0.000000,此时耦合系统进入红色区域,达到同步,之后随参数${V_{{\rm{syn}}}}$ 不断增加,红色区域逐渐变大,最后趋于稳定,说明耦合系统最后达到同步。观察图11(c),发现在$ ({k_1},D) $ 平面内,在区间$ {k_1} \in \left[ { - 1.2,0.9} \right] $ 内,$ D < 1.995 $ 时,相似函数值随耦合强度增大逐渐减小,但没有达到红色区域,说明耦合系统没有达到同步。在$ D = 1.995 $ ,$ {k_1} = 0.9 $ 时,S(0)= 0.000000,此时耦合系统达到同步,并随耦合强度增加红色区域慢慢变大,最后趋于稳定,说明耦合强度达到一定值之后,耦合系统都将处于同步状态。 图 11 系统(2)在无时滞状态下的相似函数图:(a) 反馈增益
图 11 系统(2)在无时滞状态下的相似函数图:(a) 反馈增益${k_1}$ 与参数$\alpha $ 相似函数图;(b) 反馈增益${k_1}$ 与参数${V_{{\rm{syn}}}}$ 相似函数图;(c) 反馈增益${k_1}$ 与耦合强度D相似函数图Figure 11. Similar function diagrams of system (2) without delay: (a) the feedback gain${k_1}$ and parameter$\alpha $ similarity function diagram; (b) the feedback gain${k_1}$ and parameter${V_{{\rm{syn}}}}$ similarity function diagram; (c) the feedback gain${k_1}$ and coupling strength similarity function diagram4. 结 论
本文在ML神经元的基础上,利用化学突触构造耦合神经元系统,研究了耦合系统在抑制性化学突触和兴奋性化学突触条件下同步的差别,发现耦合系统在抑制性化学突触的情况下,达到同步需要的耦合强度比兴奋性化学突触的情况下要大很多,并且达到同步之后的放电状态也不同,抑制性条件下达到同步之后,神经元不再放电,兴奋性条件下达到同步之后,神经元系统继续放电。之后在具有化学突触的神经元系统的基础上引入磁通耦合与时滞,主要以磁通反馈增益为参数研究了耦合系统的分岔与同步,单参数分岔分析中,发现时滞能够减小混沌放电增强周期放电,使耦合系统更具周期性。与单参数分岔相比,双参数分岔分析研究了多参数变化对耦合系统分岔的影响,能够更加清楚直观地观察到耦合系统的放电状态。之后对耦合系统进行单参数及双参数同步分析,发现时滞可以延迟耦合系统的同步,使耦合系统达到同步的耦合强度变大。之后利用双参数相似函数图研究了多个参数变化对耦合系统同步的影响。
-
图 2 系统(1)在抑制性条件下的时间历程图与相图:(a)
$D = 1.98$ 时的时间历程图;(b)$D = 1.98$ 时的相图;(c)$D = 2.04$ 时的时间历程图;(d)$D = 2.04$ 时的相图Figure 2. Time history diagrams and phase diagrams of system (1) under inhibition: (a) the time history diagram at time
$D = 1.98$ ; (b) the phase diagram at time$D = 1.98$ ; (c) the time history diagram at time$D = 2.04$ ; (d) the phase diagram at time$D = 2.04$ 图 3 系统(1)在兴奋性条件下的时间历程图与相图:(a)
$D = 0.081$ 时的时间历程图;(b)$D = 0.081$ 时的相图;(c)$D = 0.175$ 时的时间历程图;(d)$D = 0.175$ 时的相图Figure 3. Time history diagrams and phase diagrams of system (1) under excitatory condition: (a) the time history diagram at time
$D = 0.081$ ; (b) the phase diagram at time$D = 0.081$ ; (c) the time history diagram at time$D = 0.175$ ; (d) the phase diagram at time$D = 0.175$ 图 5 系统(2)在不同反馈增益下的时间历程图与相图:(a)
$ {k_1} = 0.2 $ 的时间历程图;(b)$ {k_1} = - 0.5 $ 的时间历程图;(c)$ {k_1} = - 1.08 $ 的时间历程图;(d)$ {k_1} = 0.2 $ 的相图;(e)$ {k_1} = - 0.5 $ 的相图;(f)$ {k_1} = - 1.08 $ 的相图Figure 5. Time history diagrams and phase diagrams of system (2) under different feedback gains: (a) the time history diagram at time
$ {k_1} = 0.2 $ ; (b) the time history diagram at time$ {k_1} = - 0.5 $ ; (c) the time history diagram at time$ {k_1} = - 1.08 $ ; (d) the phase diagram at time$ {k_1} = 0.2 $ ; (e) the phase diagram at time$ {k_1} = - 0.5 $ ; (f) the phase diagram at time$ {k_1} = - 1.08 $ 图 8 反馈增益
$ {k_1} $ ,$ {k_2} $ 与不同参数的双参数分岔图:(a)$ {k_1} $ 与$V_{\rm{K}}$ 双参数分岔图;(b)$ {k_1} $ 与$ V_{\rm Ca} $ 双参数分岔图;(c)$ {k_2} $ 与$ g_{\rm Ca} $ 双参数分岔图;(d)$ {k_2} $ 与$ g_{\rm{K}} $ 双参数分岔图Figure 8. Two-parameter bifurcation diagrams with feedback gains and different parameters: (a) the
$ {k_1} $ and$ V_{\rm{K}} $ two-parameter bifurcation diagram; (b) the$ {k_1} $ and$ V_{\rm Ca} $ two-parameter bifurcation diagram; (c) the$ {k_2} $ and$ g_{\rm Ca} $ two-parameter bifurcation diagram; (d) the$ {k_2} $ and$ g_{\rm{K}} $ two-parameter bifurcation diagram图 11 系统(2)在无时滞状态下的相似函数图:(a) 反馈增益
${k_1}$ 与参数$\alpha $ 相似函数图;(b) 反馈增益${k_1}$ 与参数${V_{{\rm{syn}}}}$ 相似函数图;(c) 反馈增益${k_1}$ 与耦合强度D相似函数图Figure 11. Similar function diagrams of system (2) without delay: (a) the feedback gain
${k_1}$ and parameter$\alpha $ similarity function diagram; (b) the feedback gain${k_1}$ and parameter${V_{{\rm{syn}}}}$ similarity function diagram; (c) the feedback gain${k_1}$ and coupling strength similarity function diagram -
[1] 寿天德. 神经生物学[M]. 北京: 高等教育出版社, 2006.SHOU Tiande. Neurobiology[M]. Beijing: Higher Education Press, 2006. (in Chinese) [2] 张艳娇, 李美生, 陆启韶. ML神经元的放电模式及时滞对神经元同步的影响[J]. 动力学与控制学报, 2009, 7(1): 19-23 doi: 10.3969/j.issn.1672-6553.2009.01.005ZHANG Yanjiao, LI Meisheng, LU Qishao. Effect of discharge mode delay of ML neurons on neuronal synchronization[J]. Journal of Dynamics and Control, 2009, 7(1): 19-23.(in Chinese) doi: 10.3969/j.issn.1672-6553.2009.01.005 [3] MA J, ZHANG G, HAYAT T, et al. Mo del electrical activity of neuron under electric field[J]. Nonlinear Dynamics, 2019, 95: 1585-1598. doi: 10.1007/s11071-018-4646-7 [4] MA J, WANG Y, WANG C, et al. Mode selection in electrical activities of myocardial cell exposed to electromagnetic radiation[J]. Chaos, Solitons and Fractals, 2017, 99: 219-255. doi: 10.1016/j.chaos.2017.04.016 [5] LV M, MA J. Multiple modes of electrical activities in a new neuron model under electromagnetic radiation[J]. Neurocomputing, 2016, 205: 375-381. doi: 10.1016/j.neucom.2016.05.004 [6] 曲良辉, 都琳, 胡海威, 等. 电磁刺激对FHN神经元系统的调控作用[J]. 动力学与控制学报, 2020, 18(1): 40-48 doi: 10.6052/1672-6553-2020-003QU Lianghui, DU Lin, HU Haiwei, et al. Regulation of FHN neuronal system by electromagnetic stimulation[J]. Journal of Dynamics and Control, 2020, 18(1): 40-48.(in Chinese) doi: 10.6052/1672-6553-2020-003 [7] SOUDEH M, FAHIMEH N, SAJAD J, et al. Chemical and electrical synapse-modulated dynamical properties of coupled neurons under magnetic flow[J]. Applied Mathematics and Computation, 2019, 348: 42-56. doi: 10.1016/j.amc.2018.11.030 [8] GUO S, XU Y, WANG C, et al. Collective response, synapse coupling and field coupling in neuronal network[J]. Chaos, Solitons and Fractals, 2017, 105: 120-127. doi: 10.1016/j.chaos.2017.10.019 [9] 王青云, 石霞, 陆启韶. 神经元耦合系统的同步动力学[M]. 北京: 科学出版社, 2008.WANG Qingyun, SHI Xia, LU Qishao. Synchronous Dynamics of Neuron Coupling Systems[M]. Beijing: Science Press, 2008. (in Chinese) [10] WANG Q, LU Q, ZHENG Y. Conduction delay-aided synchronization in two coupled Chay neurons with inhibitory synapse[J]. Journal of Biophysics, 2005, 21(6): 449-456. [11] WANG Q, LU Q, CHEN G, et al. Bifurcation and synchronization of synaptically coupled FHN models with time delay[J]. Chaos, Solitons and Fractals, 2007, 39(2): 918-925. [12] WANG Q, LU Q. Time-delay enhanced synchronization and regularization in two coupled chaotic neurons[J]. Chinese Physics Letters, 2005, 22(6): 543-546. [13] 谢一丁, 王征平, 刘帅. 复杂网络上耦合神经系统的非聚类相同步[J]. 应用数学和力学, 2020, 41(6): 627-635XIE Yiding, WANG Zhengping, LIU Shuai. Unclustered phase synchronization of coupled nervous systems on complex networks[J]. Applied Mathematics and Mechanics, 2020, 41(6): 627-635.(in Chinese) [14] 邬开俊, 单亚洲, 王春丽, 等. 时滞作用下的化学突触耦合的Hindmarsh-Rose神经元同步研究[J]. 力学季刊, 2017, 38(1): 123-134 doi: 10.15959/j.cnki.0254-0053.2017.01.014WU Kaijun, SHAN Yazhou, WANG Chunli, et al. Synchronization of chemical synaptic coupling with time delay in Hindmarsh-Rose neurons[J]. Chinese Quarterly of Mechanics, 2017, 38(1): 123-134.(in Chinese) doi: 10.15959/j.cnki.0254-0053.2017.01.014 [15] DHAMALA M, JIRSA V, DING M. Enhancement of neural synchrony by time delay[J]. Physical Review Letters, 2004, 92(7): 074104. doi: 10.1103/PhysRevLett.92.074104 [16] 李小虎, 张定一, 宋自根. 时滞耦合惯性项神经系统的多混沌路径共存[J]. 应用数学和力学, 2020, 41(6): 636-645LI Xiaohu, ZHANG Dingyi, SONG Zigen. Coexistence of multiple chaotic paths in neural systems with time-delay coupled inertial terms[J]. Applied Mathematics and Mechanics, 2020, 41(6): 636-645.(in Chinese) 期刊类型引用(0)
其他类型引用(2)
-





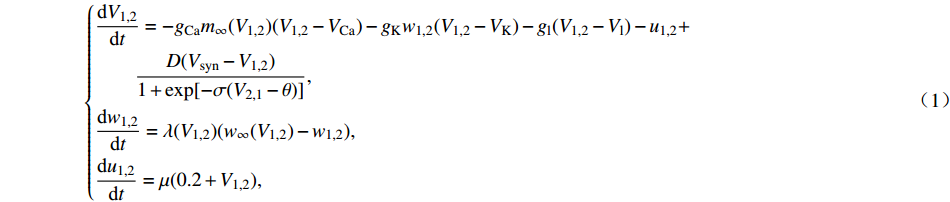
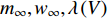
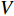
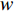
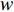
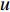
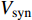
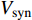
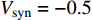
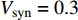
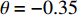
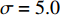
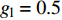
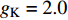
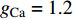
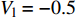
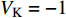
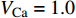
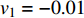
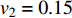
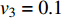
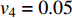
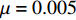
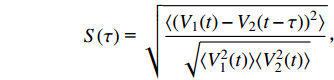
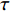
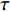
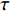
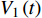
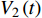
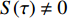
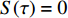
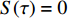
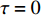
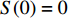
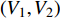
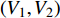

 下载:
下载:
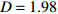
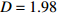
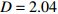
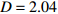
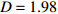
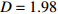
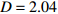
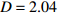
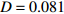
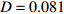
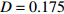
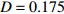
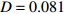
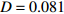
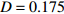
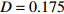
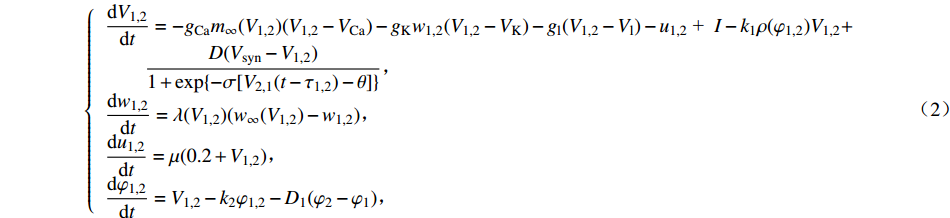
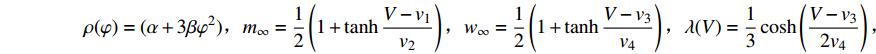
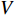
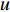
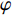
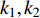
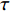
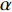
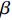
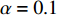
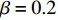
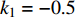
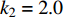
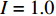
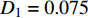
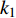
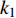
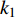
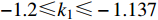
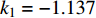
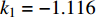
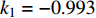
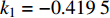
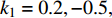
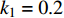
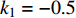
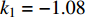

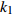
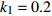
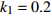
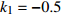
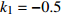
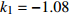
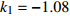
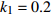
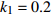
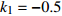
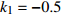
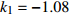
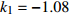
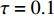
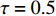
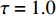

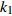
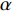
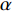
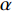
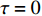
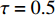
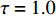

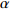
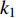
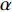
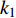
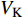
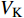
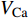
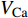
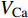
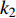
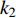
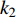
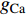
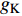
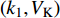
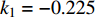
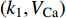
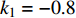
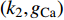
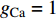
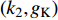
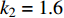
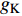
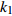
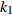
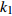
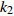
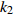
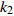
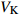
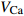
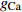
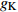
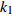
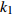
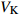
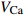
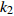
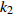
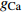
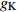
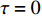
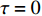
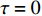
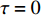
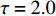
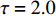
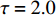
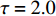


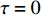
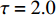
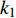
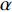
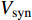
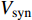
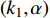
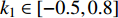
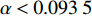
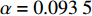
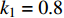
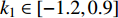
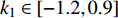
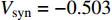
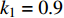
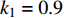
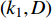
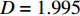
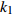
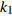
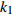
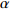
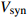
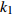
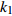
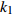
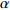
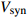
 下载:
下载:






























































 渝公网安备50010802005915号
渝公网安备50010802005915号