间断问题扩散正则化的PINN反问题求解算法

林云云; 郑素佩; 封建湖; 靳放

doi:10.21656/1000-0887.430010

间断问题扩散正则化的PINN反问题求解算法

doi: 10.21656/1000-0887.430010

长安大学理学院，西安 710064

基金项目: 国家自然科学基金（11971075）；陕西省自然科学基金青年项目（2020JQ-338；2020JQ-342）

详细信息

作者简介:
林云云（1994—），女，硕士生（E-mail：1121507157@qq.com）

郑素佩（1978—），女，副教授，博士，硕士生导师 (通讯作者. E-mail：zsp2008@chd.edu.cn)

中图分类号: O241.82; O354.5
计量
- 文章访问数: 869
- HTML全文浏览量: 747
- PDF下载量: 195
- 被引次数: 0
出版历程
- 收稿日期: 2022-01-14
- 录用日期: 2022-04-27
- 修回日期: 2022-03-17
- 网络出版日期: 2022-12-02
- 刊出日期: 2023-01-01

Diffusive Regularization Inverse PINN Solutions to Discontinuous Problems

School of Sciences, Chang’an University, Xi’an 710064, P.R.China

摘要

摘要:
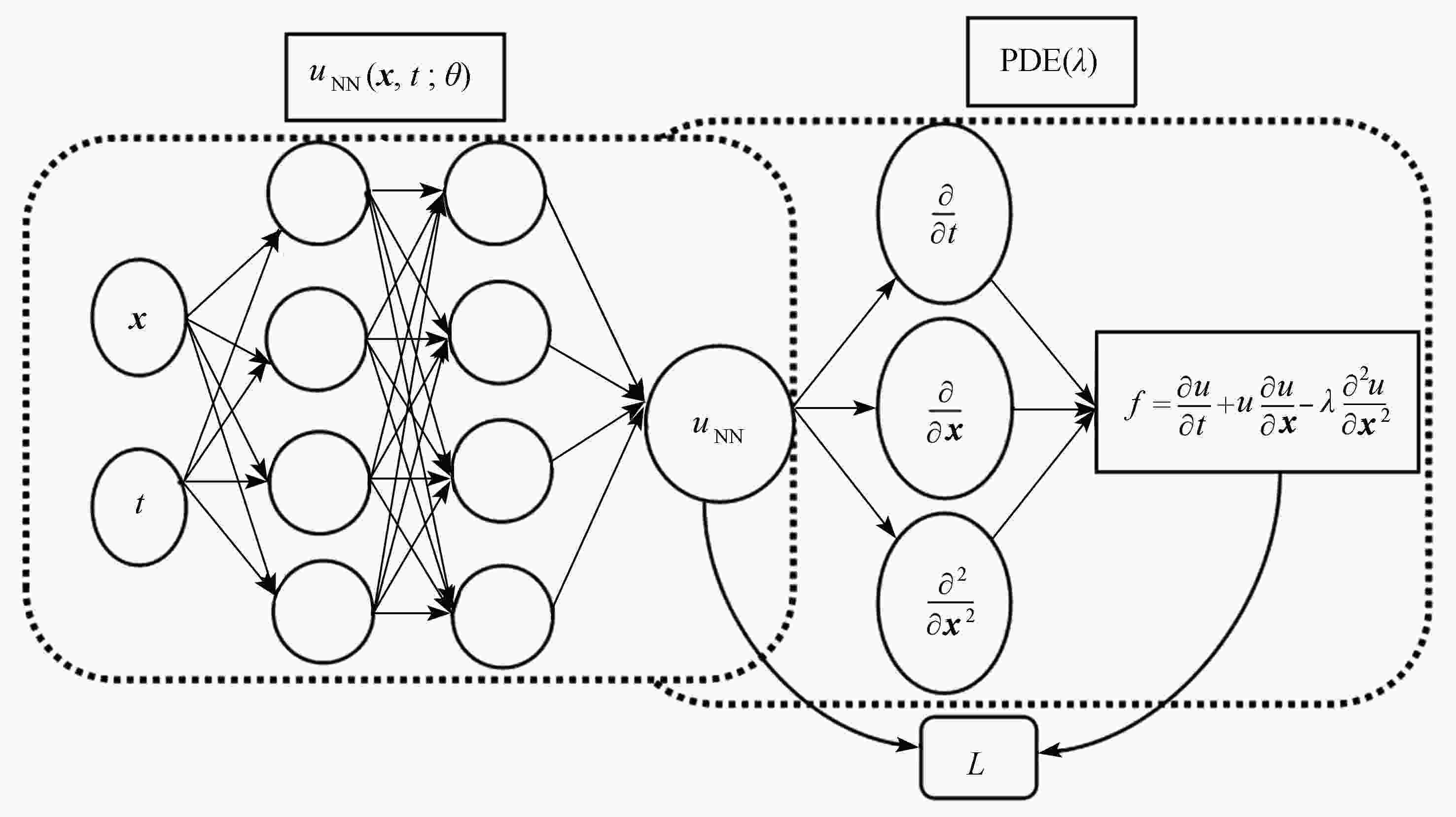
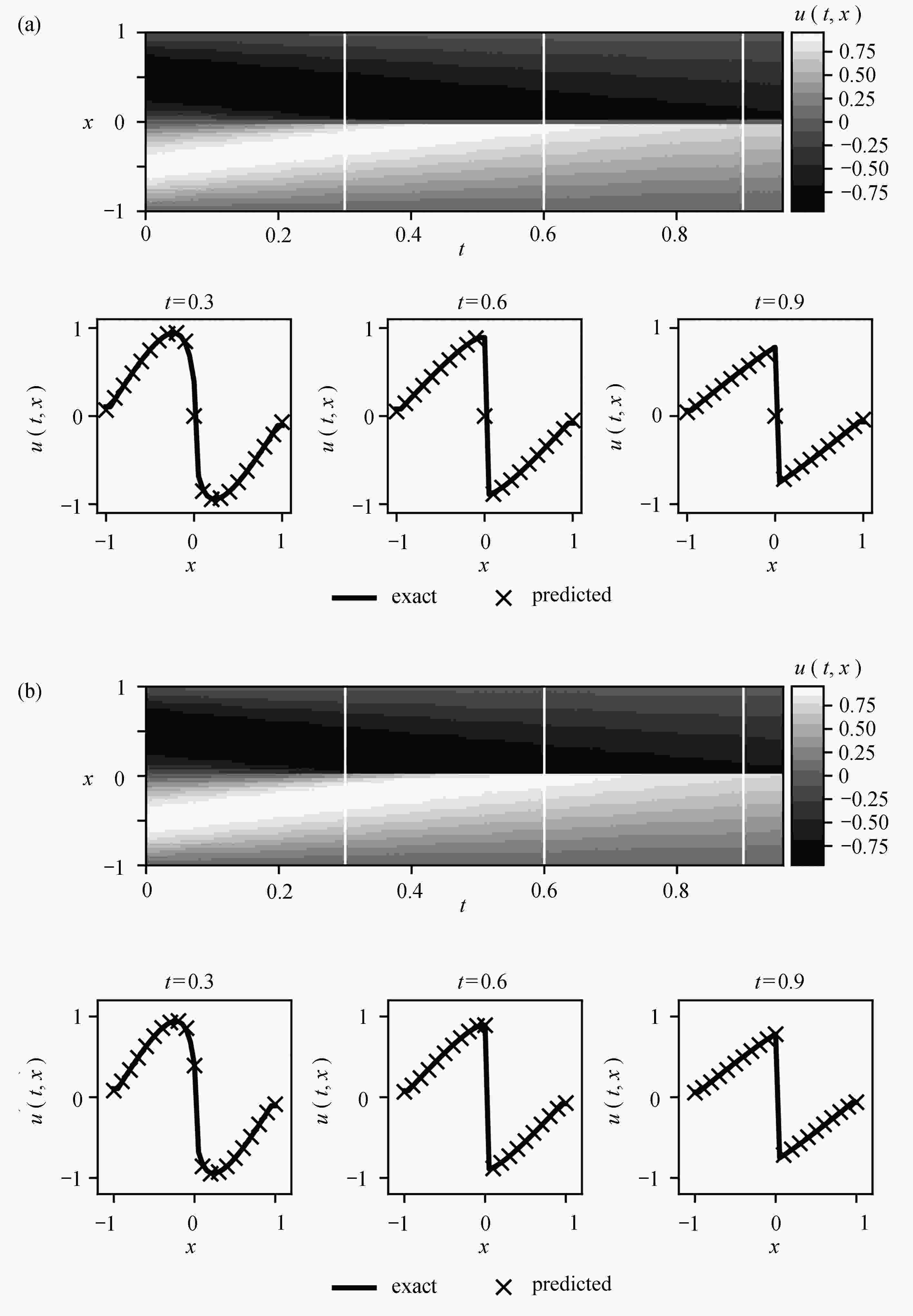
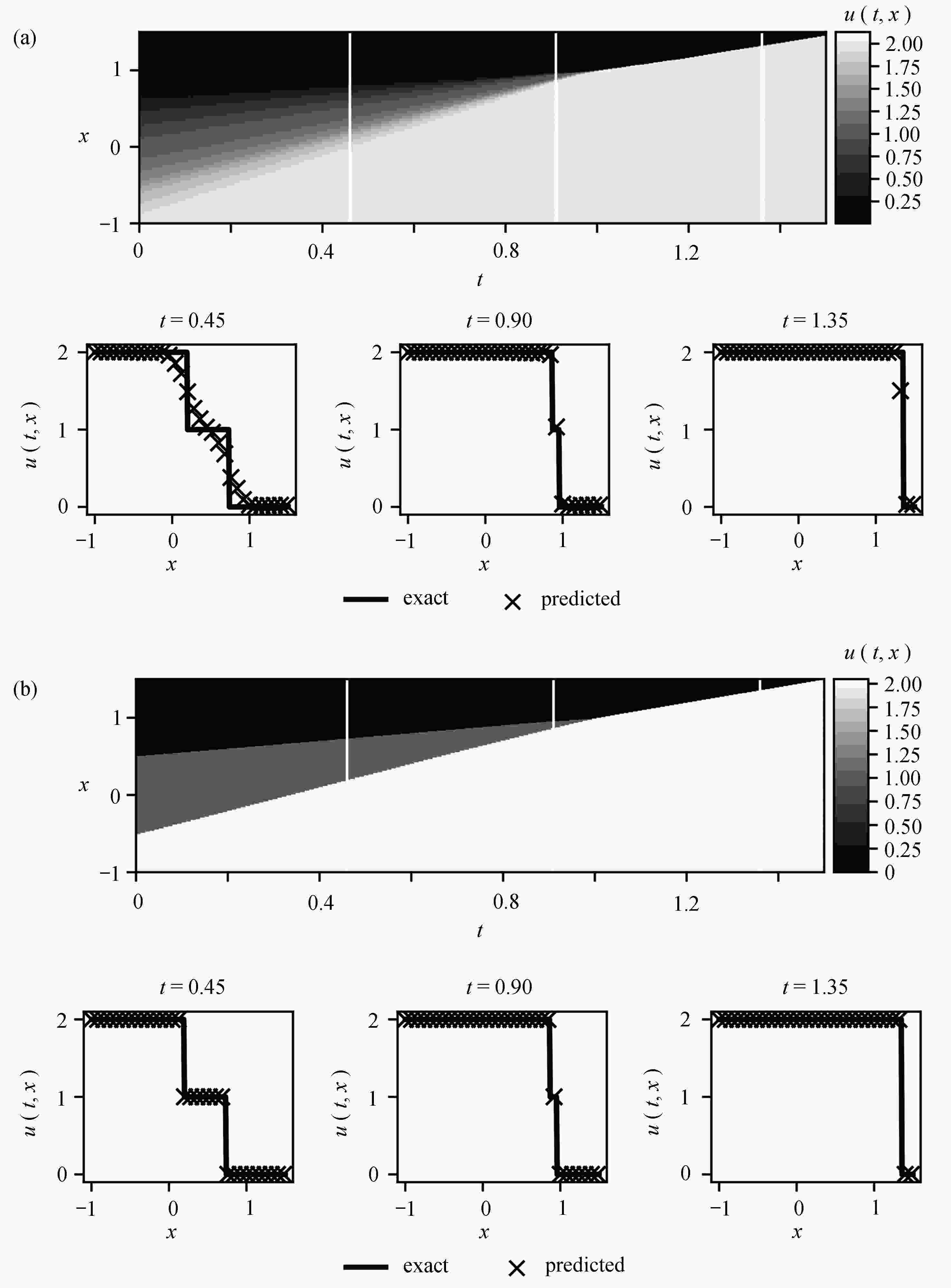
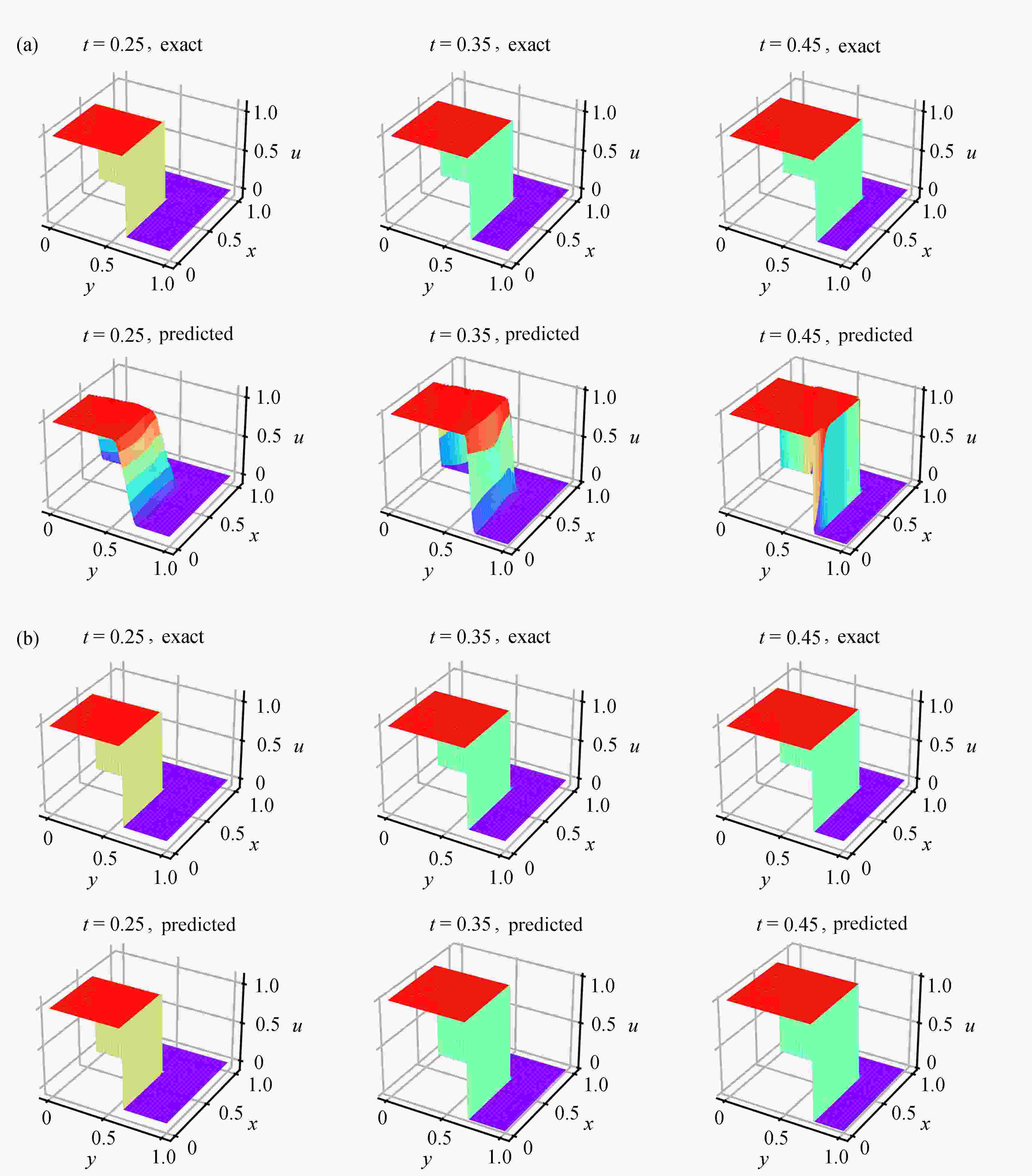
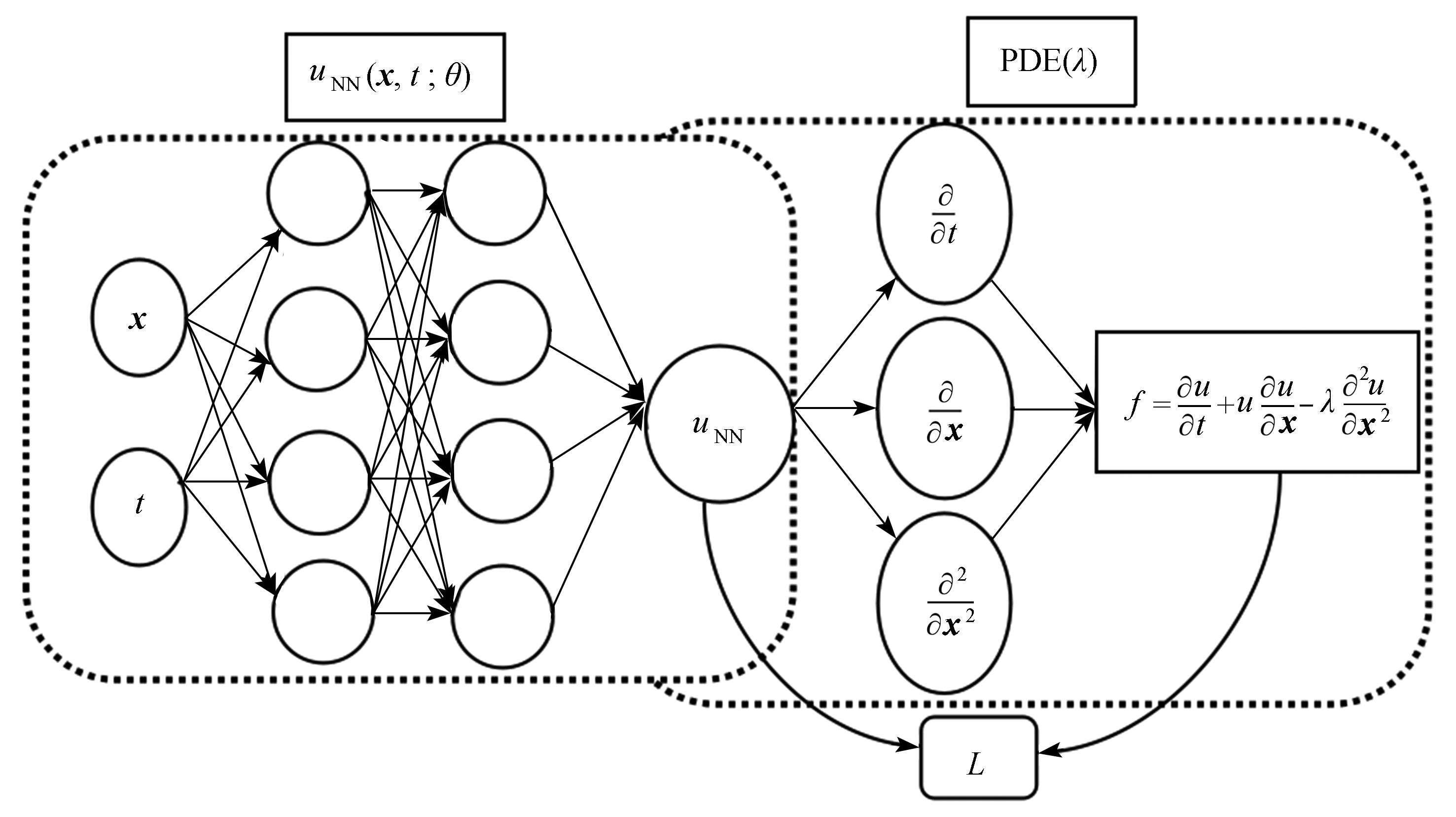
双曲守恒律方程间断问题的求解是该类方程数值求解问题研究的重点之一。采用PINN (physics-informed neural networks)求解双曲守恒律方程正问题时需要添加扩散项，但扩散项的系数很难确定，需要通过试算方法来得到，造成很大的计算浪费。为了捕捉间断并节约计算成本，对方程进行了扩散正则化处理，将正则化方程纳入损失函数中，使用守恒律方程的精确解或参考解作为训练集，学习出扩散系数，进而预测出不同时刻的解。该算法与PINN求解正问题方法相比，间断解的分辨率得到了提高，且避免了多次试算系数的麻烦。最后，通过一维和二维数值试验验证了算法的可行性，数值结果表明新算法捕捉间断能力更强、无伪振荡和抹平现象的产生，且所学习出的扩散系数为传统数值求解格式构造提供了依据。
- PINN算法 /
- 扩散正则化 /
- 反问题 /
- 无黏Burgers方程 /
- 黏性消失解
Abstract:
It is of great importance to numerically capture discontinuities for the numerical solutions to hyperbolic conservation laws equations. The PINN (physics-informed neural networks) was used to solve the forward problem of the hyperbolic conservation laws equations, with the diffusion term added, which is difficult to determine and needs to be obtained through high-cost trial calculation. To capture the discontinuous solutions and save calculation costs, the equation was regularized through addition of diffusive terms. Then the regularized equation was incorporated into the loss function, and the exact solutions or reference solutions to the conservation laws equations were used as the training set to learn the diffusion coefficients, and the solutions at different moments were predicted. Compared with that of the PINN method for solving forward problems, the resolution of discontinuous solutions was improved, and the trouble of massive trial calculation was avoided. Finally, the feasibility of the algorithm was verified by 1D and 2D numerical experiments. The numerical results show that, the new algorithm has better ability to capture discontinuities, produces no spurious oscillations and no screed phenomena. Additionally, the diffusive coefficients obtained with the new algorithm make a reference to construct the classic numerical scheme.
- PINN algorithm /
- diffusion regularization /
- inverse problem /
- inviscid Burgers’ equation /
- vanishing viscosity solution

HTML全文

图 1 网络结构示意图

Figure 1. The diagram of the network structure

下载: 全尺寸图片幻灯片

图 2 例1的数值结果对比图：(a) 未正则化方程的精确解与预测解；(b) 正则化方程的精确解与预测解

Figure 2. Comparison of numerical results for example 1: (a) exact and predicted solutions to unregularized equations; (b) exact and predicted solutions to regularized equations

下载: 全尺寸图片幻灯片

图 3 例2的数值结果对比图：(a) 未正则化方程的精确解与预测解；(b) 正则化方程的精确解与预测解

Figure 3. Comparison of numerical results for example 2: (a) exact and predicted solutions to unregularized equations; (b) exact and predicted solutions to regularized equations

下载: 全尺寸图片幻灯片

图 4 例3的数值结果对比图：(a) 未正则化方程的精确解与预测解；(b) 正则化方程的精确解与预测解

Figure 4. Comparison of numerical results for example 3: (a) exact and predicted solutions to unregularized equations; (b) exact and predicted solutions to regularized equations

下载: 全尺寸图片幻灯片

图 5 例4的数值结果对比图：(a) 未正则化方程的精确解与预测解；(b) 正则化方程的精确解与预测解

Figure 5. Comparison of numerical results for example 4: (a) exact and predicted solutions to unregularized equations; (b) exact and predicted solutions to regularized equations

下载: 全尺寸图片幻灯片

图 6 例5的数值结果对比图：(a) 未正则化方程的精确解与预测解；(b) 正则化方程的精确解与预测解

Figure 6. Comparison of numerical results for example 5: (a) exact and predicted solutions to unregularized equations; (b) exact and predicted solutions to regularized equations

下载: 全尺寸图片幻灯片

参考文献(19)

[1]	JIN X, CAI S, LI H, et al. NSFnets (Navier Stokes flow nets): physics-informed neural networks for the incompressible Navier-Stokes equations[J]. Journal of Computational Physics, 2021, 426: 109951. doi: 10.1016/j.jcp.2020.109951
[2]	BASDEVANT C, DEVILLE M, HALDENWANG P, et al. Spectral and finite difference solutions of the Burgers equation[J]. Computers & Fluids, 1986, 14(1): 23-41. doi: 10.1016/0045-7930(86)90036-8
[3]	郑素佩, 王令, 王苗苗. 求解二维浅水波方程的移动网格旋转通量法[J]. 应用数学和力学, 2020, 41(1): 42-53 ZHENG Supei, WANG Ling, WANG Miaomiao. Solution of 2D shallow water wave equation with the moving grid rotating-invariance method[J]. Applied Mathematics and Mechanics, 2020, 41(1): 42-53.(in Chinese)
[4]	贾豆, 郑素佩. 求解二维 Euler 方程的旋转通量混合格式[J]. 应用数学和力学, 2021, 42(2): 170-179 JIA Dou, ZHENG Supei. A hybrid scheme of rotational flux for solving 2D Euler equations[J]. Applied Mathematics and Mechanics, 2021, 42(2): 170-179.(in Chinese)
[5]	PSICHOGIOS D C, UNGAR L H. A hybrid neural network-first principles approach to process modeling[J]. AICHE Journal, 1992, 38(10): 1499-1511. doi: 10.1002/aic.690381003
[6]	LAGARIS I E, LIKAS A, FOTIADIS D I. Artificial neural networks for solving ordinary and partial differential equations[J]. IEEE Transactions on Neural Networks, 1998, 9(5): 987-1000. doi: 10.1109/72.712178
[7]	高普阳, 赵子桐, 杨扬. 基于卷积神经网络模型数值求解双曲型偏微分方程的研究[J]. 应用数学和力学, 2021, 42(9): 932-947 GAO Puyang, ZHAO Zitong, YANG Yang. Numerical solution of hyperbolic partial differential equations based on convolutional neural network mode[J]. Applied Mathematics and Mechanics, 2021, 42(9): 932-947.(in Chinese)
[8]	RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378(C): 686-707.
[9]	LU L, MENG X, MAO Z, et al. DeepXDE: a deep learning library for solving differential equations[J]. Society for Industrial and Applied Mathematics, 2021, 63(1): 208-228.
[10]	MAO Z, JAGTAP A D, KARNIADAKIS G E. Physics-informed neural networks for high-speed flows[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 360: 112789. doi: 10.1016/j.cma.2019.112789
[11]	LEFLOCH P G, MISHRA S. Numerical methods with controlled dissipation for small-scale dependent shocks[J]. Acta Numerica, 2014, 23: 743-816. doi: 10.1017/S0962492914000099
[12]	EL G A, HOEFER M A, SHEARER M. Dispersive and diffusive-dispersive shock waves for nonconvex conservation laws[J]. SIAM Review, 2017, 59(1): 3-61. doi: 10.1137/15M1015650
[13]	CLAMOND D, DUTYKH D. Non-dispersive conservative regularisation of nonlinear shallow water (and isentropic Euler equations)[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 55: 237-247. doi: 10.1016/j.cnsns.2017.07.011
[14]	MINBASHIAN H, GIESSELMANN J. Deep learning for hyperbolic conservation laws with non-convex flux[J]. Proceedings in Applied Mathematics and Mechanics, 2021, 20: e202000347.
[15]	LAX P. Shock waves and entropy[C]//Proceedings of a Symposium Conducted by the Mathematics Research Center, the University of Wisconsin-Madison. New York: Academic Press, 1971: 603-634.
[16]	BAYDIN A G, PEARLMUTTER B A, RADUL A A, et al. Automatic differentiation in machine learning: a survey[J]. Journal of Machine Learning Research, 2018, 18: 1-43.
[17]	KINGMA D P, BA J. Adam: a method for stochastic optimization[Z/OL]. (2017-01-30)[2022-03-17].https://arxiv.org/abs/1412.6980.
[18]	LIU D C, NOCEDAL J. On the limited memory BFGS method for large scale optimization[J]. Mathematical Programming, 1989, 45(1): 503-528.
[19]	TADMOR E. Entropy stability theory for difference approximations of nonlinear conservation laws and related time-dependent problems[J]. Acta Numerica, 2003, 12: 451-512. doi: 10.1017/S0962492902000156