Elastic Analysis of Anisotropic Functionally Graded Rotating Disks With Non-Uniform Thicknesses
-
摘要:
研究了任意梯度变化的变厚度各向异性转动圆盘的弹性问题。假设圆盘绕刚性轴匀速转动,其材料性能和厚度沿径向任意梯度变化。考虑圆盘在中心转轴处受位移约束,外侧自由,根据各向异性转动圆盘的平衡微分方程,得到关于径向应力的Fredholm积分方程,继而通过对Fredholm积分方程进行数值求解,得到结构的位移场和应力场。对具体梯度变化情况仅需代入相应梯度变化进行求解即可。数值算例部分,通过假设厚度、弹性模量等参数为特殊的幂函数形式,将由Fredholm积分方程求出的数值解与对应的精确解进行对比,以及针对常见的Voigt模型,将由该方法算得的数值解和ANSYS有限元计算结果进行对比,验证了该方法的准确性和精度。其次,针对Voigt模型,重点分析了厚度变化、材料性能梯度参数、各向异性度等对应力场和位移场的影响。提出了针对材料性能和厚度沿径向呈任意梯度变化的圆盘结构弹性分析方法,将为优化功能梯度圆盘的结构和材料参数、有效调整构件应力分布、提高结构安全性,提供强有力的工具;算例分析结果对功能梯度圆盘在复杂条件下的结构安全设计有重要的理论指导意义。
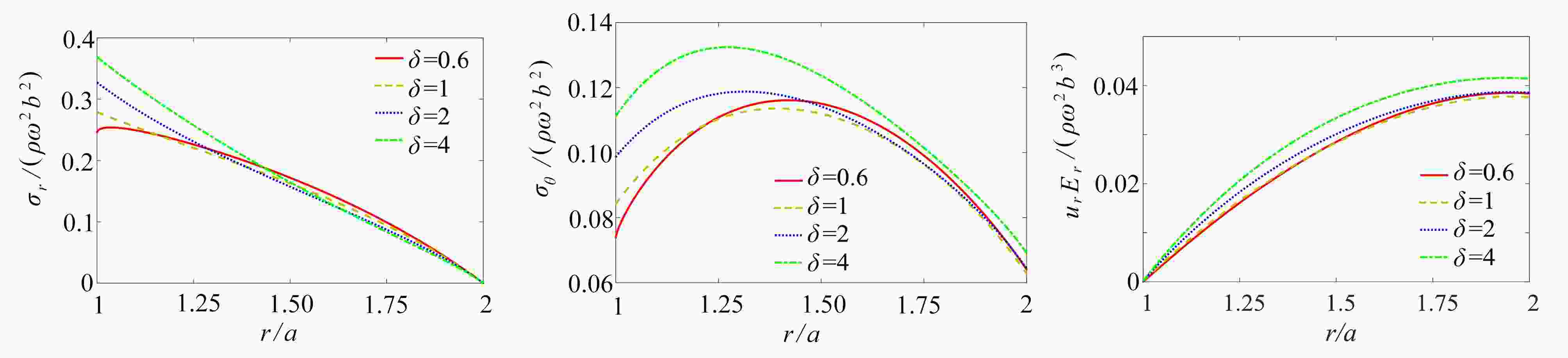
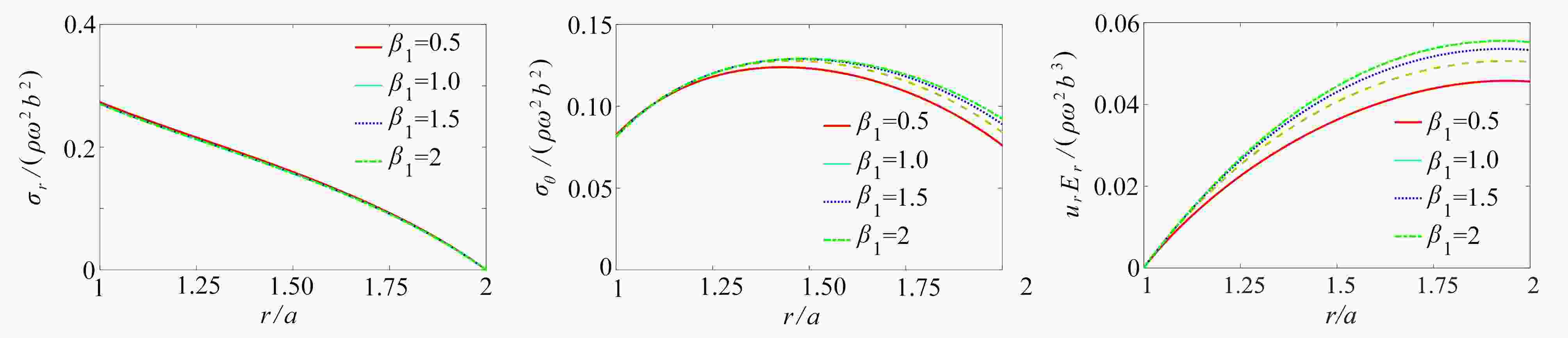
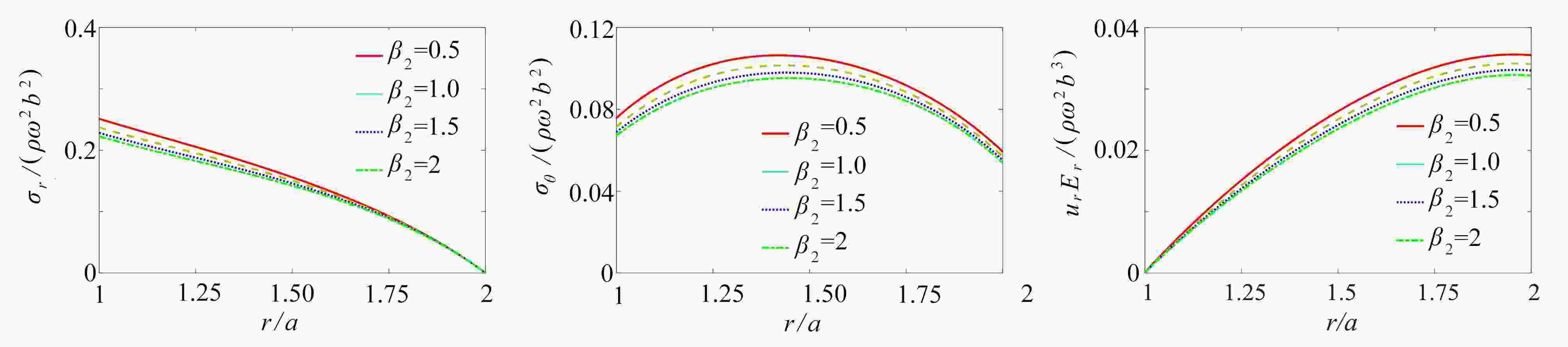
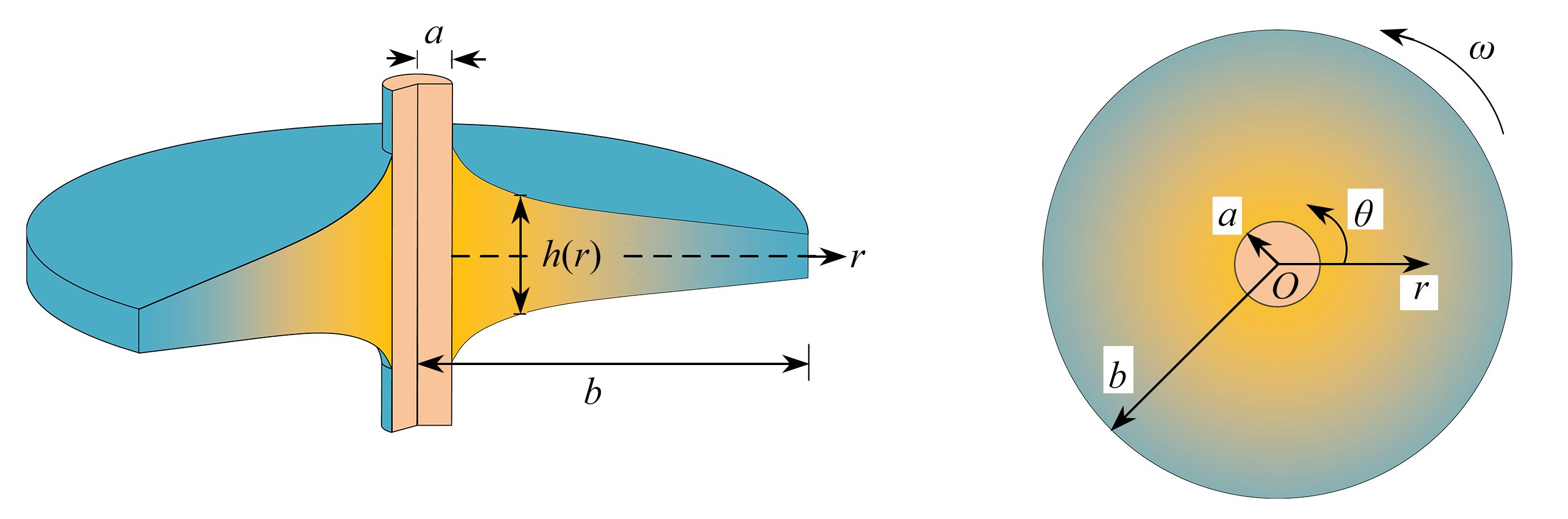
Abstract:The elastic problem of anisotropic functionally graded rotating disks with non-uniform thicknesses was studied. The material properties and thicknesses of the disk change with an arbitrary gradient along the radial direction, and the disk displacement is constrained at the central axis of rotation and the edge is free. According to the equilibrium differential equations for the anisotropic rotating disk, the Fredholm integral equation of radial stresses was obtained, and then numerically solved to calculate the displacement and stress fields. For any specific situation of gradient change, it is only needed to substitute the corresponding gradient parameters into the equation for solution. In the numerical examples, firstly, the parameters such as the thickness and the elastic modulus were assumed to be of special power functions. The numerical solutions obtained from the Fredholm integral equation were compared with the corresponding exact solutions and the FEM solutions by the ANSYS software for the common Voigt model, to validate the method. Then, the effects of the thickness change, the gradient parameters and different degrees of anisotropy on the stress and displacement fields, were numerically analyzed with the common Voigt model. The proposed elastic analysis method for disk structures with arbitrary gradient changes along the radial direction, is promising in the application of structural optimization. The analysis results can guide the engineers to design safer and more economical functionally graded structures.
-
Key words:
- functionally graded materials /
- arbitrary gradient change /
- anisotropy /
- rotating disk /
- elasticity
-
-
[1] REN Y, ZHANG J A, JONATHAN V, et al. An observational study of the symmetric boundary layer structure and tropical cyclone intensity[J]. Atmosphere, 2020, 11(2): 158-172. doi: 10.3390/atmos11020158 [2] ZHU A, ZHANG F, GAO R, et al. Increasing polarization-dependent SERS effects by optimizing the axial symmetry of plasmonic nanostructures[J]. Applied Surface Science, 2019, 494: 87-93. doi: 10.1016/j.apsusc.2019.07.182 [3] WANG Y Z, ZAN C, LIU D, et al. Generalized solution of the thermoelastic problem for the axisymmetric structure with temperature-dependent properties[J]. European Journal of Mechanics A:Solids, 2019, 76: 346-354. doi: 10.1016/j.euromechsol.2019.05.004 [4] CHAKRADHAR K S, RAO V M. Three different compact elliptical slot ultra-wide band antennas for wireless communication applications[J]. Journal of Communications, 2021, 16(2): 52-59. [5] 唐鑫, 朱如鹏, 廖梅军, 等. 第三代航空齿轮钢圆柱齿轮弯曲疲劳强度性能测试分析[J]. 航空动力学报, 2021, 36(8): 1756-1764.TANG Xin, ZHU Rupeng, LIAO Meijun, et al. Analyses bending fatigue strength test of cylindrical gear of third-generation aviation gear steel[J]. Journal of Aerospace Power, 2021, 36(8): 1756-1764. (in Chinese) [6] AHMED S N, REDDY P R, VENKATESH S. Thermal impact of disk design on aircraft engine compressor disks[J]. International Journal of New Innovations in Engineering and Technology, 2019, 12(2): 26-42. [7] TIMOSHENKO S P, GOODIER J N. Theory of Elasticity[M]. McGraw Hill Higher Education, 1970. [8] 马涛, 赵忠民, 刘良祥, 等. 功能梯度材料的研究进展及应用前景[J]. 化工科技, 2012, 20(1): 71-75 doi: 10.3969/j.issn.1008-0511.2012.01.019MA Tao, ZHAO Zhongmin, LIU Liangxiang, et al. The research development and future application of functionally gradient materials[J]. Science & Technology in Chenmical Industry, 2012, 20(1): 71-75.(in Chinese) doi: 10.3969/j.issn.1008-0511.2012.01.019 [9] HUANG Y. Bending and free vibrational analysis of bi-directional functionally graded beams with circular cross-section[J]. Applied Mathematics and Mechanics, 2020, 41(10): 1497-1516. doi: 10.1007/s10483-020-2670-6 [10] ZENKOUR A M. Stress distribution in rotating composite structures of functionally graded solid disks[J]. Journal of Materials Processing Technology, 2009, 209(7): 3511-3517. doi: 10.1016/j.jmatprotec.2008.08.008 [11] DAI T, DAI H L. Thermo-elastic analysis of a functionally graded rotating hollow circular disk with variable thickness and angular speed[J]. Applied Mathematical Modelling, 2016, 40(17/18): 7689-7707. [12] ABDALLA H M A, CASAGRANDE D, MORO L. Thermo-mechanical analysis and optimization of functionally graded rotating disks[J]. Latin American Journal of Solids and Structures, 2016, 13(5): 819-834. doi: 10.1590/1679-78252420 [13] KALALI A T, HADIDI M S, BEHROOZ H. Elasto-plastic stress analysis in rotating disks and pressure vessels made of functionally graded materials[J]. Latin American Journal of Solids & Structures, 2016, 13(5): 819-834. [14] BOSE T, RATTAN M. Modeling creep behavior of thermally graded rotating disc of functionally graded material[J]. Differential Equations and Dynamical Systems, 2021, 29(2): 285-298. doi: 10.1007/s12591-017-0350-1 [15] 沈景凤, 张翠, 刘方. 基于热弹性耦合理论的功能梯度材料薄壁旋转碟片力学性能[J]. 复合材料学报, 2019, 36(4): 1017-1028 doi: 10.13801/j.cnki.fhclxb.20180626.003SHEN Jingfeng, ZHANG Cui, LIU Fang. Thermally coupled analysis of thermoelastic field in a thin-walled rotating FGM circular disk[J]. Acta Materiae Compositae Sinica, 2019, 36(4): 1017-1028.(in Chinese) doi: 10.13801/j.cnki.fhclxb.20180626.003 [16] MADAN R, SAHA K, BHOWMICK S. Limit elastic analysis of rotating annular disks having sigmoid-FGM composition based on MROM[J]. World Journal of Engineering, 2019, 16(6): 806-813. doi: 10.1108/WJE-05-2019-0155 [17] 张莹, 梅靖, 陈鼎, 等. 功能梯度圆板和环板受周边力作用的弹性力学解[J]. 应用数学和力学, 2018, 39(5): 538-547ZHANG Ying, MEI Jing, CHEN Ding, et al. Elasticity solutions for functionally graded circular and annular plates subjected to boundary forces and moments[J]. Applied Mathematics and Mechanics, 2018, 39(5): 538-547.(in Chinese) [18] LI X Y, DING H J, CHEN W Q. Elasticity solutions for a transversely isotropic functionally graded circular plate subject to an axisymmetric transverse load qr k[J]. International Journal of Solids and Structures, 2008, 45(1): 191-210. doi: 10.1016/j.ijsolstr.2007.07.023 [19] LI X Y, DING H J, CHEN W Q. Three-dimensional analytical solution for functionally graded magneto-electro-elastic circular plates subjected to uniform load[J]. Composite Structures, 2008, 83(4): 381-390. doi: 10.1016/j.compstruct.2007.05.006 [20] PENG X L, LI X F. Effects of gradient on stress distribution in rotating functionally graded solid disks[J]. Journal of Mechanical Science & Technology, 2012, 26(5): 1483-1492. [21] 彭旭龙, 李显方. 任意梯度分布功能梯度圆环的热弹性分析[J]. 应用数学和力学, 2009, 30(10): 1135-1142 doi: 10.3879/j.issn.1000-0887.2009.10.001PENG Xulong, LI Xianfang. Thermoelastic analysis of a functionally graded annulus with an arbitrary gradient[J]. Applied Mathematics and Mechanics, 2009, 30(10): 1135-1142.(in Chinese) doi: 10.3879/j.issn.1000-0887.2009.10.001 [22] OZTURK M, ERDOGAN F. Mode Ⅰ crack problem in an inhomogeneous orthotropic medium[J]. International Journal of Engineering Science, 1997, 35(9): 869-883. doi: 10.1016/S0020-7225(97)80005-5 [23] YILDIRIM V. Numerical/analytical solutions to the elastic response of arbitrarily functionally graded polar orthotropic rotating discs[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2018, 40(6): 1-21. [24] MAHDAVI E, GHASEMI A, ALASHTI R A. Elastic-plastic analysis of functionally graded rotating disks with variable thickness and temperature-dependent material properties under mechanical loading and unloading[J]. Aerospace Science & Technology, 2016, 59: 57-68. [25] YILDIRIM S, TUTUNCU N. Rotational instability of polar orthotropic nonuniform disks[C]//8th International Conference on Mechanical and Aerospace Engineering (ICMAE). IEEE, 2017: 586-580. -





 下载:
下载:








 渝公网安备50010802005915号
渝公网安备50010802005915号