Three-Point Bending Properties of Carbon Fiber Reinforced Polymer Composite Honeycomb Sandwich Structures With Curved Wall
-
摘要:
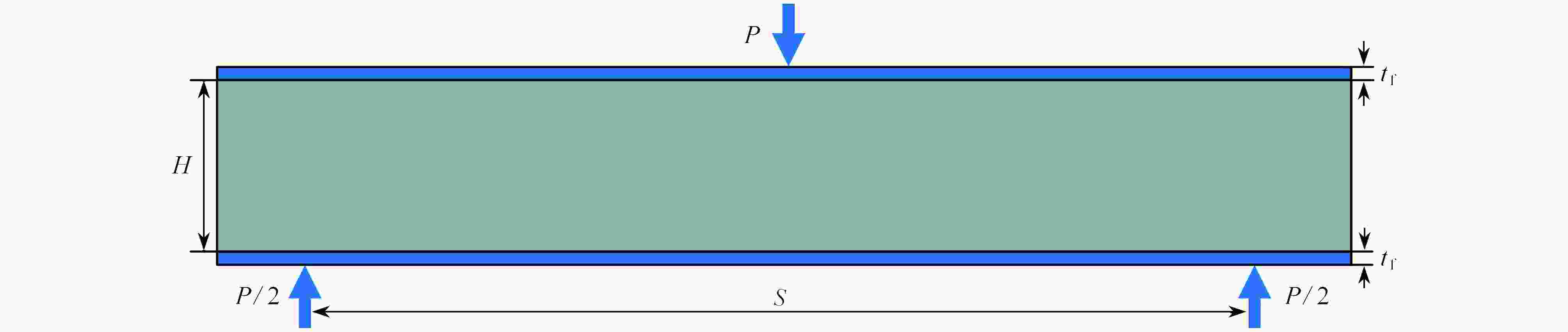
为研究碳纤维复合材料(CFRP)曲壁蜂窝结构在三点弯曲载荷作用下的承载特性与失效模式，对不同芯层高度、面板厚度的结构进行了理论预报、数值模拟及试验。首先，根据夹芯结构的主要失效模式，提出了相应的理论预报公式，并绘制了失效机制图；其次，建立了CFRP曲壁蜂窝夹芯结构的有限元仿真模型，对其在三点弯曲载荷作用下的典型失效行为进行模拟；最后，通过模压成型工艺制备了不同尺寸的CFRP曲壁蜂窝夹芯结构，并将试验结果与理论、模拟结果进行比较。结果表明，蜂窝夹芯结构承载能力与芯层高度、面板厚度密切相关，结构芯层及面板刚度随其尺寸的减小而下降，导致结构失效模式由面芯脱黏失效变为面板压溃失效。
Abstract:In order to analyze the load-bearing capacities and failure modes of carbon fiber reinforced polymer composite honeycomb sandwich structures with curved wall under 3-point bending loads, theoretical prediction, numerical simulation and tests were carried out for structures with different core heights and facesheet thicknesses. According to the main failure modes of sandwich structures, different theoretical prediction formulas and failure mechanism diagrams were firstly made. Then, the numerical simulation model for the CFRP sandwich structure with a honeycomb core was established to simulate its failure behavior under the 3-point bending load. Finally, different-size CFRP sandwich structures were fabricated by a molding process, and the experimental results were compared with theoretical and simulation results. The results show that, the bearing capacity of the sandwich structure is positively correlated with the core height and the facesheet thickness, and the core and facesheet stiffness decrease with the structure size, which results in the structural failure modes changing from core-facesheet debonding to face crushing.
-
Key words:
- composite /
- honeycomb /
- sandwich structure /
- 3-point bending
-
图 1 复合材料蜂窝夹芯结构三点弯曲试验示意图
Figure 1. The test schematic diagram of the composite honeycomb sandwich structure under 3-point bending load
图 3 曲壁蜂窝夹芯结构制备流程
Figure 3. The preparation process of the honeycomb sandwich structure with curved wall
图 7 试验与数值模拟载荷-位移曲线
注 为了解释图中的颜色，读者可以参考本文的电子网页版本。
Figure 7. Load-displacement curves of test and simulation
表 1 碳纤维/树脂基复合材料力学性能
Table 1. Mechanical properties of carbon fiber reinforced polymer composites
parameter value parameter value parameter value E1/GPa 149.6 G12/MPa 4 000 $ \sigma _3^{\text{T}} $/MPa 28 E2/GPa 8.7 G13/MPa 4 000 $ \sigma _3^{\text{C}} $/MPa 191 E3/GPa 8.7 G23/MPa 3 000 ${\tau _{12}} $/MPa 73 ${\mu _{12}} $ 0.3 $ \sigma _1^{\text{T}} $/MPa 2 444 ${\tau _{13}} $/MPa 73 ${\mu _{13}} $ 0.3 $ \sigma _1^{\text{C}} $/MPa 1 000 ${\tau _{23}} $/MPa 73 ${\mu _{23}} $ 0.3 $ \sigma _2^{\text{T}} $/MPa 28 σlay/MPa 25 $ \sigma _2^{\text{C}} $/MPa 191 
下载: 导出CSV
表 2 试件几何尺寸
Table 2. The geometry of specimens
specimen core length l/mm core width b/mm core height H/mm facesheet thickness tf /mm A 196 74.5 30.4 0.76 B 196 74.1 15.3 0.76 C 196 74.2 15.5 0.26
下载: 导出CSV
表 3 试件的其他参数
Table 3. Other parameters of specimens
specimen number of layers (core) angle of each layer (core) number of layers (face) angle of each layer (face) quality M/g A 3 [0°/90°/0°] 8 [0°/90°/±45°]2s 122.8 B 3 [0°/90°/0°] 8 [0°/90°/±45°]2s 85 C 3 [0°/90°/0°] 3 [0°/90°/0°] 62.7
下载: 导出CSV
表 4 试件A、B及C理论预测、模拟及试验结果
Table 4. Results of specimens A, B and C obtained through theory, simulation and experiment
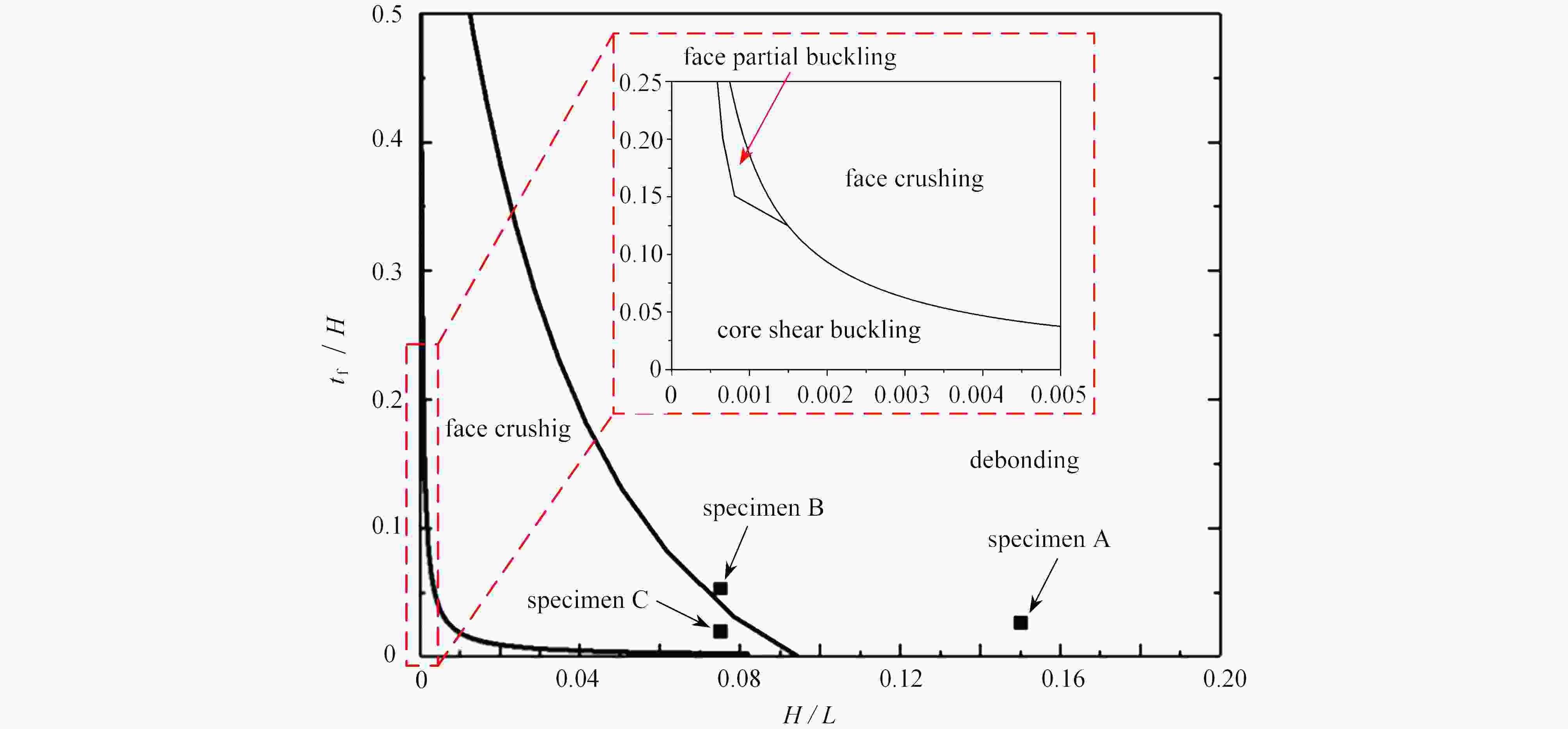
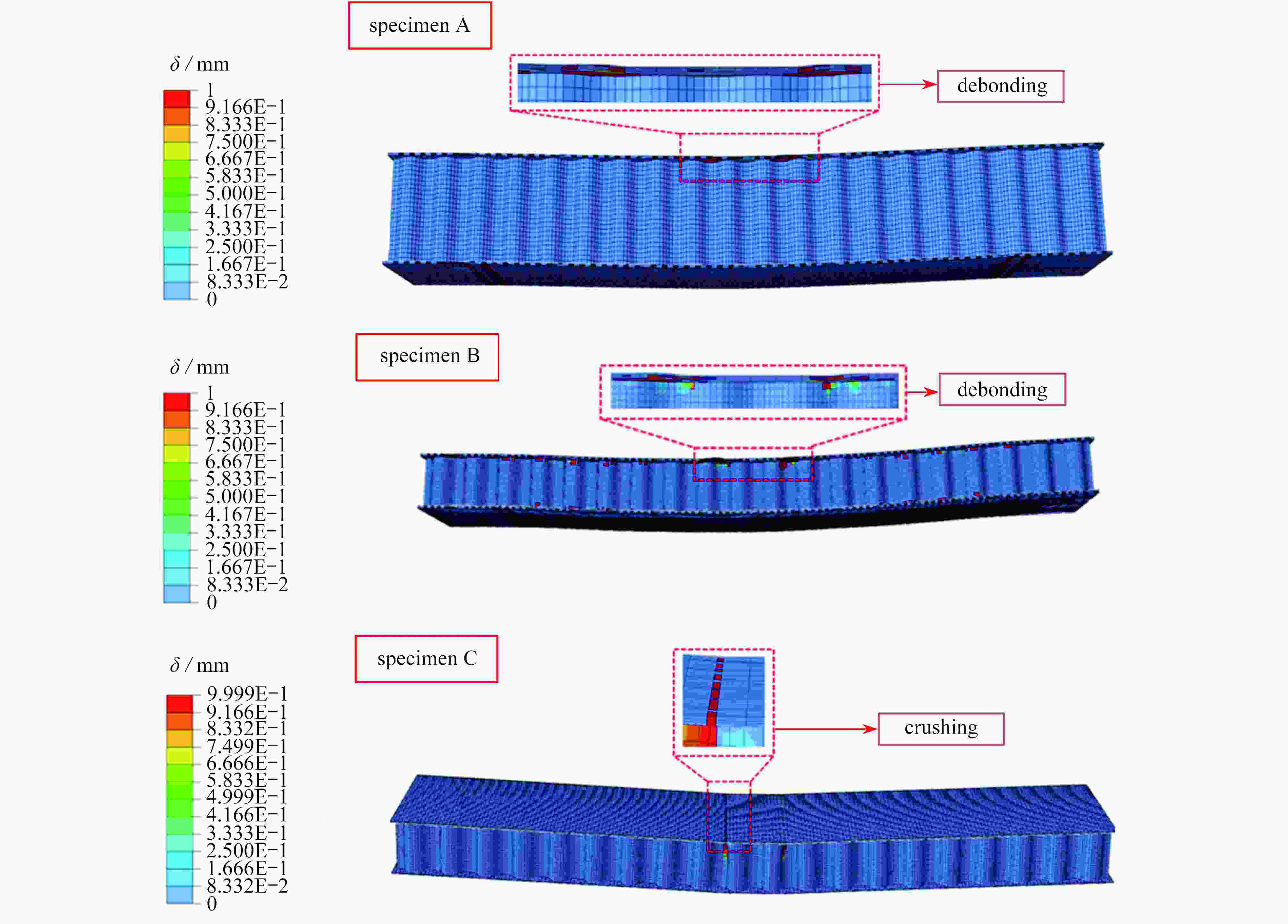
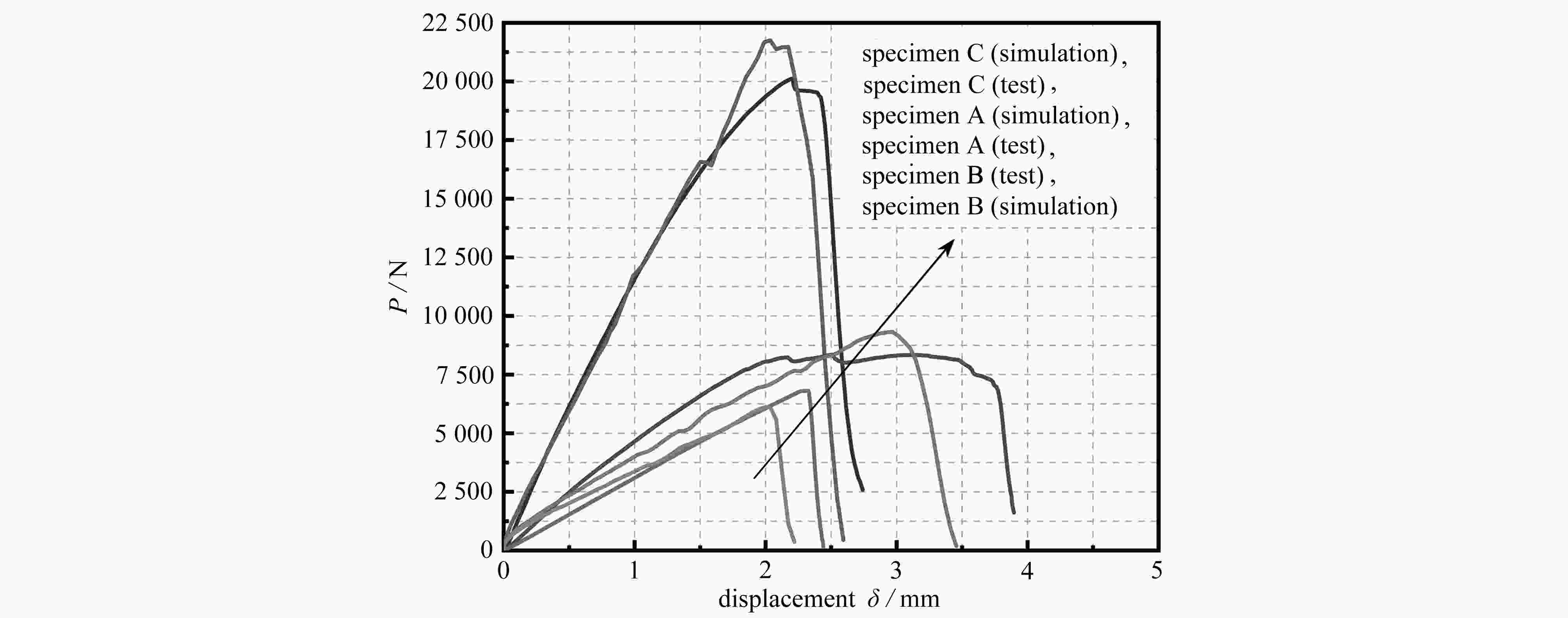
specimen theoretical failure mode numerical failure mode experimental failure mode Pt /N Pn /N Pe /N (Pe−Pt)/Pe (Pn−Pe)/Pn A debonding debonding debonding 17 952 21 755 20 103.9 0.107 0.076 B debonding debonding debonding 10 176 9 324.4 8 237.5 −0.235 0.116 C face crushing face crushing face crushing 7 286.7 6 119.6 6 814.5 −0.068 −0.114
下载: 导出CSV
-
[1] 王永福, 漆文凯, 沈承. 弹性约束边界条件下矩形蜂窝夹芯板的自由振动分析[J]. 应用数学和力学, 2019, 40(6): 583-594. (WANG Yongfu, QI Wenkai, SHEN Cheng. Free vibration analysis of rectangular honeycomb-cored plates under elastically constrained boundary conditions[J]. Applied Mathematics and Mechanics, 2019, 40(6): 583-594.(in Chinese) [2] THOMAS T, TIWARI G. Crushing behavior of honeycomb structure: a review[J]. International Journal of Crashworthiness, 2019, 24(5): 555-579. doi: 10.1080/13588265.2018.1480471 [3] LIANG H, SONG B, PENG P, et al. Preparation of three-dimensional honeycomb carbon materials and their adsorption of Cr (Ⅵ)[J]. Chemical Engineering Journal, 2019, 367: 9-16. doi: 10.1016/j.cej.2019.02.121 [4] IVANEZ I, FERNANDEZ-CAÑADAS L M, SANCHEZ-SAEZ S. Compressive deformation and energy-absorption capability of aluminium honeycomb core[J]. Composite Structures, 2017, 174: 123-133. doi: 10.1016/j.compstruct.2017.04.056 [5] YANG W, ZHANG X, YANG K, et al. Shear property characterization of aramid paper and its application to the prediction of honeycomb behaviors[J]. Composite Structures, 2020, 254: 112800. doi: 10.1016/j.compstruct.2020.112800 [6] UDDIN M, GANDY H T, RAHMAN M M, et al. Adhesiveless honeycomb sandwich structures of prepreg carbon fiber composites for primary structural applications[J]. Advanced Composites and Hybrid Materials, 2019, 2(2): 339-350. doi: 10.1007/s42114-019-00096-6 [7] 杨志韬, 于国财, 刘鑫, 等. 多级复合材料蜂窝结构的力学性能[J]. 复合材料学报, 2019, 36(9): 2110-2118.YANG Zhitao, YU Guocai, LIU Xin, et al Mechanical properties of hierarchical composite honeycomb structures[J]. Acta Materiae Compositae Sinica, 2019, 36(9): 2110-2118.(in Chinese) [8] WANG J, SHI C, YANG N, et al. Strength, stiffness, and panel peeling strength of carbon fiber-reinforced composite sandwich structures with aluminum honeycomb cores for vehicle body[J]. Composite Structures, 2018, 184: 1189-1196. doi: 10.1016/j.compstruct.2017.10.038 [9] RUSSELL B, DESHPANDE V, WADLEY H. Quasistatic deformation and failure modes of composite square honeycombs[J]. Journal of Mechanics of Materials and Structures, 2008, 3(7): 1315-1340. doi: 10.2140/jomms.2008.3.1315 [10] CÔTÉ F, FLECK N, DESHPANDE V. Fatigue performance of sandwich beams with a pyramidal core[J]. International Journal of Fatigue, 2007, 29(8): 1402-1412. doi: 10.1016/j.ijfatigue.2006.11.013 [11] 孟卫华, 王建军, 米栋, 等. 航空发动机用蜂窝材料应变率相关本构模型及应用研究[J]. 应用数学和力学, 2018, 39(6): 665-671. (MENG Weihua, WANG Jianjun, MI Dong, et al. Application of strain-rate-dependent material models to aero-engine honeycomb casing analysis[J]. Applied Mathematics and Mechanics, 2018, 39(6): 665-671.(in Chinese) [12] QIU K, WANG Z, ZHANG W. The effective elastic properties of flexible hexagonal honeycomb cores with consideration for geometric nonlinearity[J]. Aerospace Science and Technology, 2016, 58: 258-266. doi: 10.1016/j.ast.2016.08.026 [13] KESHAVANARAYANA S R, SHAHVERDI H, KOTHARE A, et al. The effect of node bond adhesive fillet on uniaxial in-plane responses of hexagonal honeycomb core[J]. Composite Structures, 2017, 175: 111-122. doi: 10.1016/j.compstruct.2017.05.010 [14] LU J L, LUO W, LI X Y, et al. Two-dimensional node-line semimetals in a honeycomb-kagome lattice[J]. Chinese Physics Letters, 2017, 34(5): 057302. doi: 10.1088/0256-307X/34/5/057302 [15] CHEN H J, TSAI S W. Analysis and optimum design of composite grid structures[J]. Journal of Composite Materials, 1996, 30(4): 503-534. doi: 10.1177/002199839603000405 [16] RUSSELL B, LIU T, FLECK N, et al. Quasi-static three-point bending of carbon fiber sandwich beams with square honeycomb cores[J]. Journal of Applied Mechanics-Transactions of the ASME, 2011, 78(3): 031008. doi: 10.1115/1.4003221 [17] 范华林, 金丰年, 方岱宁. 格栅结构力学性能研究进展[J]. 力学进展, 2008, 38(1): 35-52. (FAN Hualin, JIN Fengnian, FANG Daining. Structural mechanics of lattice grids[J]. Advances in Mechanics, 2008, 38(1): 35-52.(in Chinese) doi: 10.3321/j.issn:1000-0992.2008.01.002 [18] ALLEN H G. Analysis and Design of Structural Sandwich Panels[M]. Elsevier, 2013. -
计量
- 文章访问数: 1478
- HTML全文浏览量: 487
- PDF下载量: 161
- 被引次数: 0
渝公网安备50010802005915号