热传导问题杂交基本解有限元法虚拟源点的探究

张凯; 王克用; 齐东平

doi:10.21656/1000-0887.430077

热传导问题杂交基本解有限元法虚拟源点的探究

doi: 10.21656/1000-0887.430077

上海工程技术大学机械与汽车工程学院，上海 201620

基金项目:

上海市自然科学基金项目 19ZR1421400

详细信息

作者简介:
张凯(1996—)，男，硕士生(E-mail: kai_zhangly@163.com)

通讯作者:
王克用(1975—)，男，副教授，博士(通讯作者. E-mail: keyong_wang@126.com)

中图分类号: O242.21;O343.1
计量
- 文章访问数: 436
- HTML全文浏览量: 169
- PDF下载量: 49
- 被引次数: 0
出版历程
- 收稿日期: 2022-03-10
- 修回日期: 2022-05-15
- 刊出日期: 2023-04-01

Research on the Fictitious Source Points of the Hybrid Fundamental Solution-Based Finite Element Method for Heat Conduction Problems

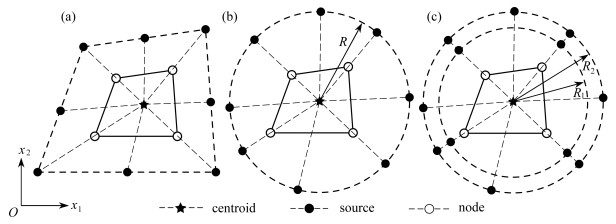
School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, P.R.China

摘要

摘要: 针对热传导问题，提出了杂交基本解有限元法. 首先，假设两个独立场：一个为利用基本解线性组合近似的单元域内温度场，另一个为使用与传统有限元法相同形式的辅助网线温度场. 然后，利用修正变分泛函将上述两个独立场关联起来，并导出有限元列式. 然而，该方法的准确性很大程度上取决于源点的分布和数量，通常将源点布置在单元外部两种虚拟边界上：与单元相似的边界和圆形边界. 此外，还提出了双重虚拟边界，并与上述两种源点布局方式进行对比. 通过两个典型数值算例，验证了该文方法在不同源点布局下的有效性和对网格畸变的不敏感性.
- 基本解 /
- 有限元法 /
- 修正变分泛函 /
- 虚拟边界 /
- 网格畸变
Abstract: The hybrid fundamental solution-based finite element method was proposed for heat conduction problems. Firstly, 2 independent fields were assumed: the intra-element temperature field approximated through the linear combination of fundamental solutions, and the auxiliary frame temperature field in the same form as that in the conventional finite element method. Then, a modified variational functional was employed to link the 2 independent fields and derive the finite element formulation. However, the accuracy of the method is strongly dependent on the distribution and the number of source points. The source points were usually placed on 2 fictitious boundaries outside the element: one is similar to the element shape, the other is a circular one. Furthermore, the dual fictitious boundary scheme was proposed for comparison with the above fictitious boundaries. With different configurations of source points, 2 typical numerical examples were given to demonstrate the validity and the insensitivity to mesh distortion of the proposed method.
- fundamental solution /
- finite element method /
- modified variational functional /
- fictitious boundary /
- mesh distortion

HTML全文

图 1 源点配置方式

Figure 1. Configurations of source points

下载: 全尺寸图片幻灯片

图 2 典型四节点单元和单元边形函数

Figure 2. A typical 4-node element and the element side shape functions

下载: 全尺寸图片幻灯片

图 3 正方形板与有限元网格

Figure 3. A square plate and the finite element meshes

下载: 全尺寸图片幻灯片

图 4 不同源点数目的四节点单元

Figure 4. A 4-node element with different numbers of source points

下载: 全尺寸图片幻灯片

图 5 无量纲参数λ对计算精度的影响

Figure 5. Effects of dimensionless parameter λ on the computation accuracy

下载: 全尺寸图片幻灯片

图 6 无量纲参数λ对矩阵H_e条件数的影响

Figure 6. Effects of dimensionless parameter λ on the condition number of matrix H_e

下载: 全尺寸图片幻灯片

图 7 网格畸变方案

Figure 7. Mesh distortion schemes

下载: 全尺寸图片幻灯片

图 8 畸变程度ψ对计算精度影响

Figure 8. Effects of distortion parameter ψ on the computation accuracy

下载: 全尺寸图片幻灯片

图 9 网格密度对计算精度的影响

Figure 9. Effects of the mesh density on the computation accuracy

下载: 全尺寸图片幻灯片

图 10 偏心环空与有限元网格

Figure 10. An eccentric annulus and the finite element meshes

下载: 全尺寸图片幻灯片

图 11 偏心环空温度u的等值线图

Figure 11. Contour plots of temperature u in the eccentric annulus

下载: 全尺寸图片幻灯片

图 12 单元形心处温度u沿周向的变化

Figure 12. Variations of temperature u at element centroids along the circumferential direction

下载: 全尺寸图片幻灯片

图 13 单元形心处热流分量q_x₁和q_x₂沿周向的变化

Figure 13. Variations of heat flux components q_x₁ and q_x₂ at element centroids along the circumferential direction

下载: 全尺寸图片幻灯片

表 1 选择点处温度u的计算结果

Table 1. Computation results for temperature u at the selected points

x₁	x₂	source point type	HFS-FEM				ABAQUS
x₁	x₂	source point type	2×2 mesh	4×4 mesh	6×6 mesh	8×8 mesh	25×25 mesh
0.02	0.48	1	40.375 3	40.410 3	40.418 2	40.420 7
		2	40.375 3	40.410 3	40.418 2	40.420 7	40.422 1
		3	40.403 3	40.417 4	40.420 1	40.421 1
0.1	0.1	1	48.027 5	48.102 9	48.119 0	48.119 9
		2	48.027 5	48.102 9	48.119 0	48.119 9	48.123 8
		3	48.027 7	48.107 0	48.116 2	48.119 7
0.34	0.44	1	41.304 1	41.453 3	41.479 8	41.480 2
		2	41.304 1	41.453 3	41.479 8	41.480 2	41.487 0
		3	41.286 2	41.447 3	41.479 7	41.487 8

下载: 导出CSV

表 2 选择点处热流分量q_x₂的计算结果

Table 2. Computation results for heat flux component q_x₂ at the selected points

x₁	x₂	source point type	HFS-FEM				ABAQUS
x₁	x₂	source point type	2×2 mesh	4×4 mesh	6×6 mesh	8×8 mesh	25×25 mesh
0.02	0.48	1	20.180 5	20.882 7	21.002 7	21.044 3
		2	20.180 5	20.882 6	21.002 7	21.044 3	21.097 4
		3	20.111 2	20.863 1	21.010 0	21.062 4
0.1	0.1	1	19.710 3	18.918 4	19.091 4	18.908 6
		2	19.710 3	18.918 4	19.091 5	18.908 6	18.931 8
		3	19.731 5	19.105 3	18.922 1	18.929 5
0.34	0.44	1	21.594 2	24.337 3	24.853 8	24.148 8
		2	21.594 2	24.337 3	24.853 8	24.148 7	24.469 7
		3	21.446 9	23.796 8	23.991 0	24.084 1

下载: 导出CSV

表 3 CPU时间的对比

Table 3. Comparation of the CPU time

method	element	CPU time t_CPU/s
HFS-FEM (type 3)	78	0.07
ABAQUS	78	0.1
ABAQUS	300	0.2

下载: 导出CSV

参考文献(19)

[1]	JIROUSEK J, LEON N. A powerful finite element for plate bending[J]. Computer Methods in Applied Mechanics & Engineering, 1977, 12(1): 77-96.
[2]	JIROUSEK J, VENKATESH A. Hybrid Trefftz plane elasticity elements with p-method capabilities[J]. International Journal for Numerical Methods in Engineering, 1992, 35(7): 1443-1472. doi: 10.1002/nme.1620350705
[3]	QIN Q H, WANG H. MATLAB and C Programming for Trefftz Finite Element Methods[M]. Boca Raton: CRC Press, 2008.
[4]	WANG H, QIN Q H. Hybrid FEM with fundamental solutions as trial functions for heat conduction simulation[J]. Acta Mechanica Solida Sinica, 2009, 22(5): 487-498. doi: 10.1016/S0894-9166(09)60300-1
[5]	SHE Z, WANG K Y, LI P C. Thermal analysis of multilayer coated fiber-reinforced composites by the hybrid Trefftz finite element method[J]. Composite Structures, 2019, 224: 110992. doi: 10.1016/j.compstruct.2019.110992
[6]	WEISSER S. Arbitrary order Trefftz-like basis functions on polygonal meshes and realization in BEM-based FEM[J]. Computers & Mathematics With Applications, 2014, 67(7): 1390-1406.
[7]	ZHOU J C, WANG K Y, LI P C, MIAO X D. Hybrid fundamental solution based finite element method for axisymmetric potential problems[J]. Engineering Analysis With Boundary Elements, 2018, 91: 82-91. doi: 10.1016/j.enganabound.2018.03.009
[8]	ZHOU J C, WANG K Y, LI P C. Hybrid fundamental solution based finite element method for axisymmetric potential problems with arbitrary boundary conditions[J]. Computers & Structures, 2019, 212: 72-85.
[9]	秦庆华. Hybrid-Trefftz有限元法的研究进展[J]. 力学进展, 1998, 28(1): 71-82. doi: 10.3321/j.issn:1000-0992.1998.01.006 QIN Qinghua. Advances in hybrid-Trefftz finite element method[J]. Advances in Mechanics, 1998, 28(1): 71-82. (in Chinese) doi: 10.3321/j.issn:1000-0992.1998.01.006
[10]	王克用, 黄争鸣, 李培超, 等. 正交各向异性轴对称位势问题的Trefftz有限元分析[J]. 应用数学和力学, 2013, 34(5): 462-469. doi: 10.3879/j.issn.1000-0887.2013.05.004 WANG Keyong, HUANG Zhengming, LI Peichao, et al. Trefftz finite element analysis of axisymmetric potential problems in orthotropic media[J]. Applied Mathematics and Mechanics, 2013, 34(5): 462-469. (in Chinese) doi: 10.3879/j.issn.1000-0887.2013.05.004
[11]	CAO C Y, QIN Q H, YU A B. Micromechanical Analysis of heterogeneous composites using hybrid Trefftz FEM and hybrid fundamental solution based FEM[J]. Journal of Mechanics, 2013, 29(4): 661-674. doi: 10.1017/jmech.2013.54
[12]	WANG H, QIN Q H. Fundamental-solution-based finite element model for plane orthotropic elastic bodies[J]. European Journal of Mechanics A: Solids, 2010, 29(5): 801-809. doi: 10.1016/j.euromechsol.2010.05.003
[13]	CAO C Y, QIN Q H. Hybrid fundamental solution based finite element method: theory and applications[J]. Advances in Mathematical Physics, 2015, 2015: 916029.
[14]	WANG K Y, ZHOU J C, ZENG R Y. Hybrid Trefftz finite element method for axisymmetric elasticity problems under torsion[J]. Materials Today Communications, 2021, 27: 102420. doi: 10.1016/j.mtcomm.2021.102420
[15]	WANG H, LIN W, QIN Q H. Fundamental-solution-based hybrid finite element with singularity control for two-dimensional mixed-mode crack problems[J]. Engineering Analysis With Boundary Elements, 2019, 108: 267-278. doi: 10.1016/j.enganabound.2019.08.016
[16]	周枫林, 谢贵重, 张见明, 等. 角度-距离复合变换法消除边界积分方程近奇异性[J]. 应用数学和力学, 2020, 41(5): 530-540. doi: 10.21656/1000-0887.400229 ZHOU Fenglin, XIE Guizhong, ZHANG Jianming, et al. Near-singularity cancellation with the angle-distance transformation method for boundary integral equations[J]. Applied Mathematics and Mechanics, 2020, 41(5): 530-540. (in Chinese) doi: 10.21656/1000-0887.400229
[17]	GRABSKI J K, KARAGEORGHIS A. Moving pseudo-boundary method of fundamental solutions for nonlinear potential problems[J]. Engineering Analysis With Boundary Elements, 2019, 105: 78-86. doi: 10.1016/j.enganabound.2019.04.009
[18]	GORZELAŃCZYK P, KOŁODZIEJ J A. Some remarks concerning the shape of the source contour with application of the method of fundamental solutions to elastic torsion of prismatic rods[J]. Engineering Analysis With Boundary Elements, 2008, 32(1): 64-75. doi: 10.1016/j.enganabound.2007.05.004
[19]	潘文峰, 戴海. 具有双重虚拟边界的基本解方法求解Stokes问题[J]. 中国科技论文, 2018, 13(5): 563-567. doi: 10.3969/j.issn.2095-2783.2018.05.015 PAN Wenfeng, DAI Hai. Method of fundamental solutions with double fictitious boundaries for solving Stokes problems[J]. China Sciencepaper, 2018, 13(5): 563-567. (in Chinese) doi: 10.3969/j.issn.2095-2783.2018.05.015