Interlaminar Crack Propagation Analysis of ENF Specimens Based on the Cohesive Zone Model
-
摘要:
基于经典层合板理论及黏聚区模型，针对纯Ⅱ型断裂ENF试件的裂纹扩展，建立了含一般分层裂纹层合板的理论模型。相较于传统的梁理论，该文模型充分考虑了黏聚区的软化过程，引入了试件发生失效前的非线性行为，预测的失效载荷小于梁理论结果，与文献试验值更为接近。相比于梁理论（仅包含断裂韧性单一参数），该文模型可同时分析界面强度、断裂韧性及界面初始刚度对ENF试件载荷-位移曲线的影响。结果表明：界面强度主要影响试件失效前的力学行为，对裂纹扩展基本无影响，断裂韧性是影响裂纹扩展的主要参数，界面初始刚度仅影响线弹性加载段；黏聚区长度随断裂韧性增大而增大，随界面强度增大而减小；相较于断裂韧性，界面强度对黏聚区长度的影响更为明显；黏聚区尖端到达试件半长处时，黏聚区的长度呈现一定程度的减小。
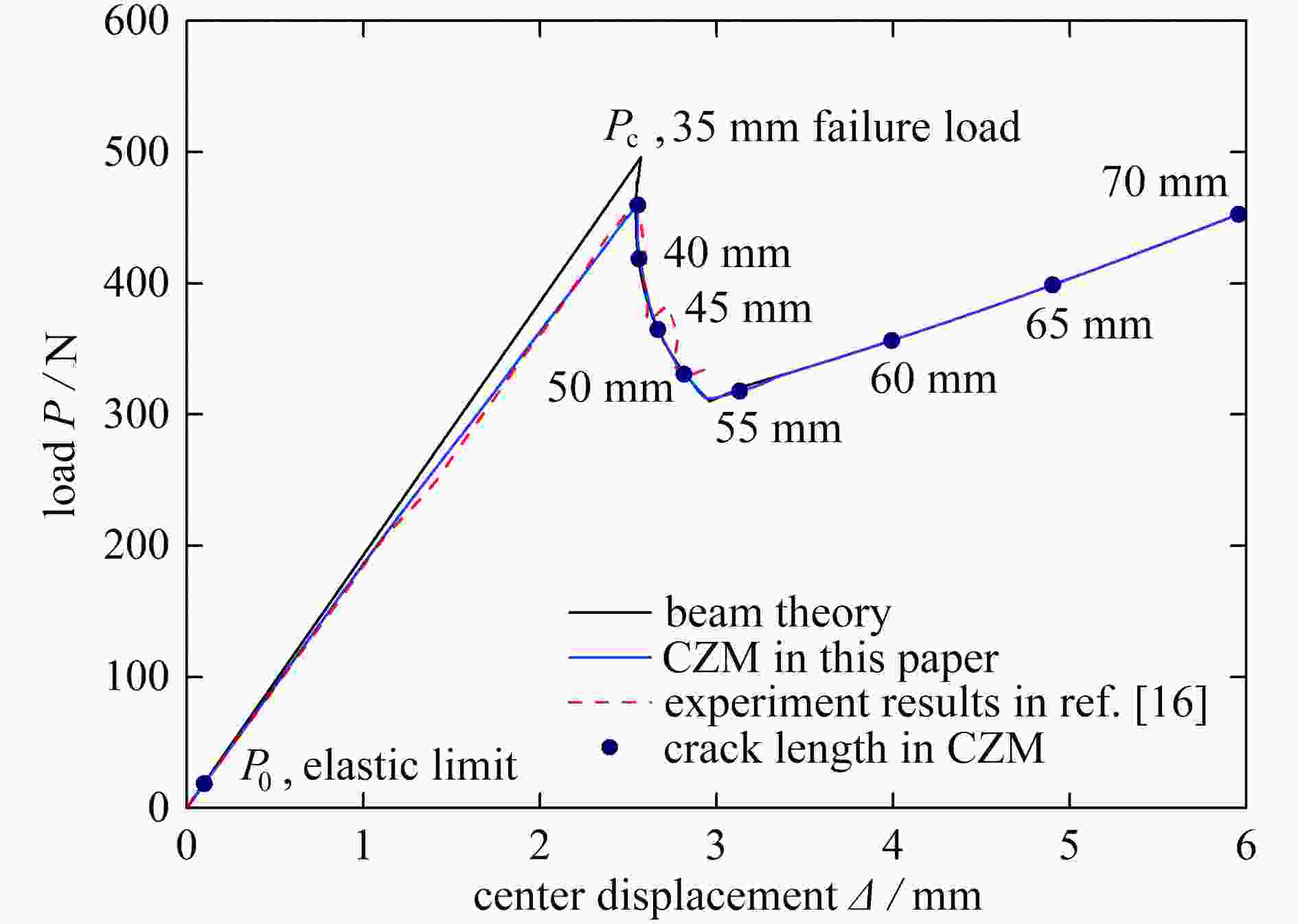
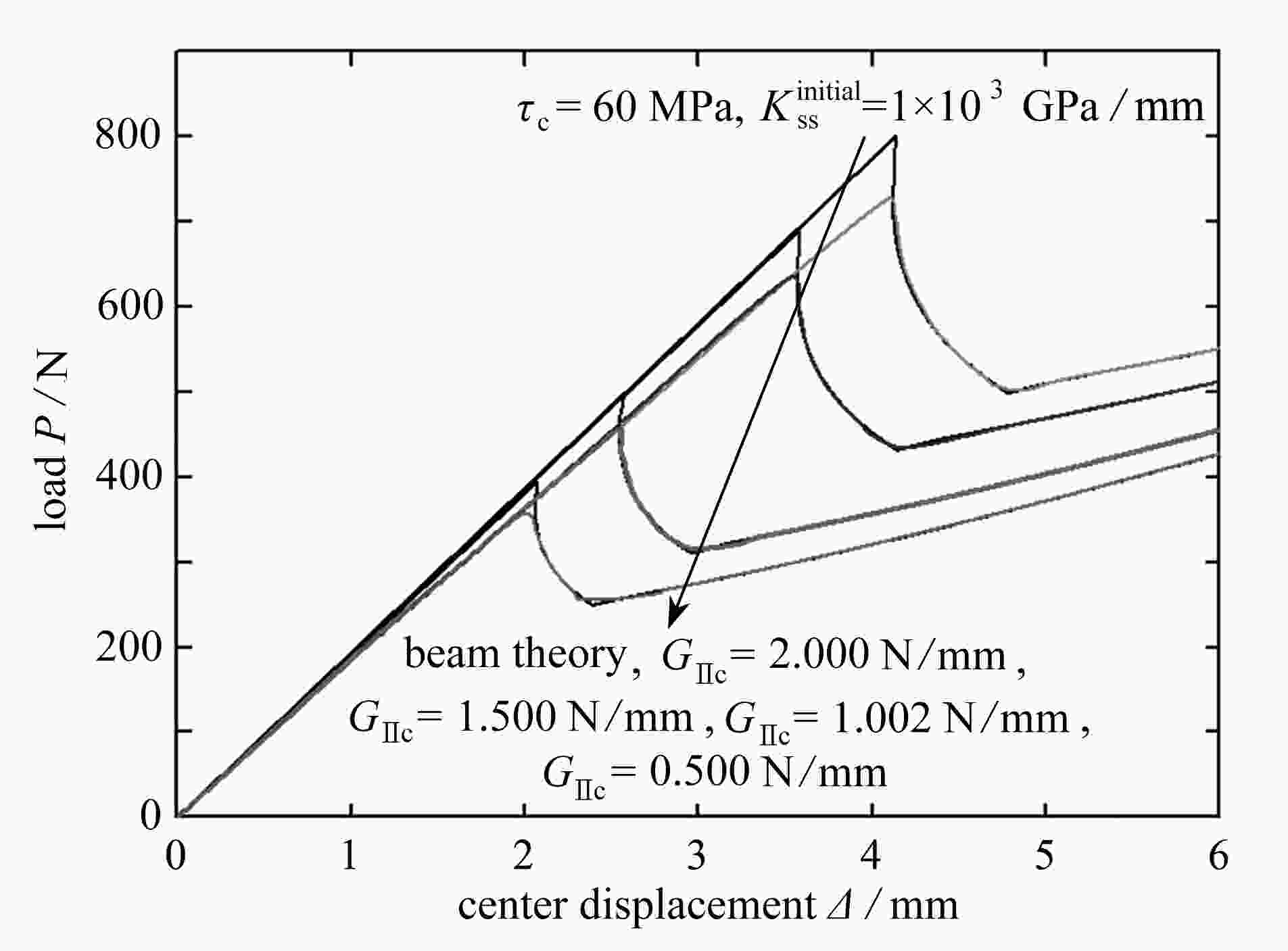
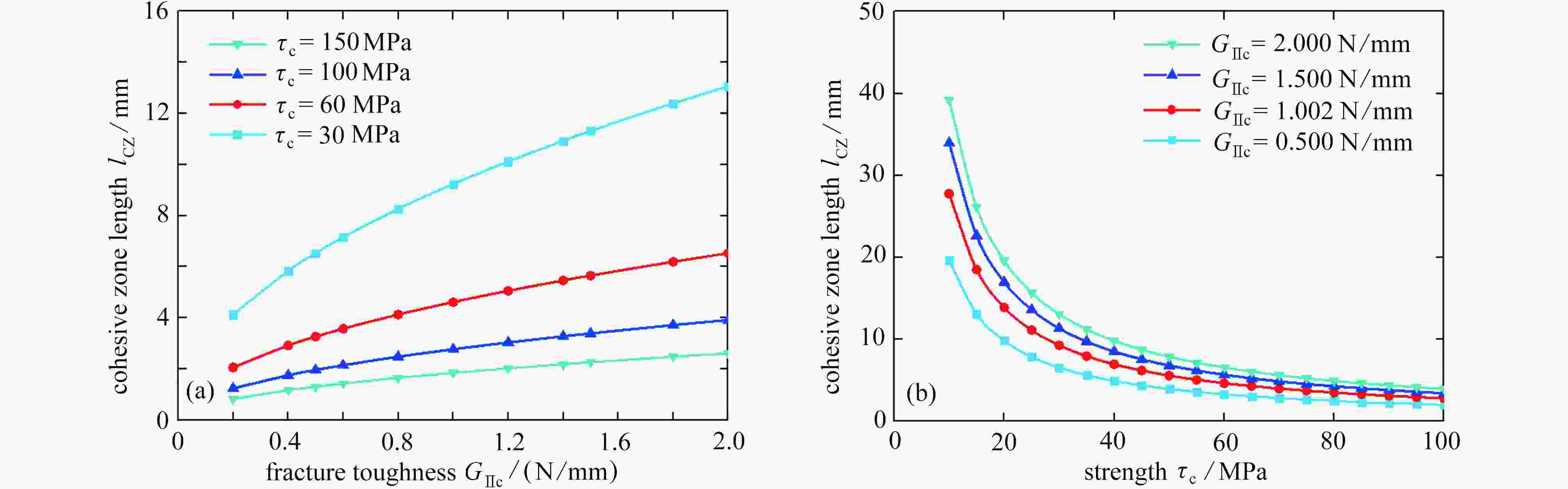
Abstract:Based on the classical laminated plate theory and the cohesive zone model, a theoretical model for general delamination cracked laminates was established for crack propagation of pure mode Ⅱ ENF specimens. Compared with the conventional beam theory, the proposed model fully considered the softening process of the cohesive zone and introduced the nonlinear behavior of ENF specimens before failure. The predicted failure load is smaller than that under the beam theory and closer to the experimental data in literatures. Compared with the beam theory with only fracture toughness considered, the proposed model can simultaneously analyze the influences of the interface strength, the fracture toughness and the initial interface stiffness on the load-displacement curves in ENF tests. The results show that, the interface strength mainly affects the mechanical behavior of specimens before failure, but has no influence on crack propagation. The fracture toughness is the main parameter affecting crack propagation, and the initial interface stiffness only affects the linear elastic loading stage. The cohesive zone length increases with the fracture toughness and decreases with the interface strength. The effect of the interface strength on the cohesive zone length is more obvious than that of the fracture toughness. When the adhesive zone tip reaches the half length of the specimen, the adhesive zone length will decrease to a certain extent.
-
Key words:
- ENF test /
- delamination /
- cohesive zone /
- crack
-
图 1 层合板黏聚区微元受力分析
Figure 1. Microelement stress analysis of the cohesive zone of the laminates
图 6 界面强度对ENF试件载荷-位移曲线的影响
Figure 6. Influences of the interfacial strength on load-displacement curves of the ENF specimen
图 7 断裂韧性对ENF试件载荷-位移曲线的影响
Figure 7. Influences of the fracture toughness on load-displacement curves of the ENF specimen
图 8 Ⅱ型界面初始刚度的影响：(a)载荷-位移曲线；(b)Ⅱ型裂纹T-S本构关系
Figure 8. Influences of the initial stiffness of the mode Ⅱ interfaces: (a) load-displacement curves; (b) T-S constitutive relationships of the mode Ⅱ crack
图 9 Ⅱ型裂纹黏聚区长度随裂纹扩展的变化趋势
Figure 9. Variation tendencies of the cohesive zone length of the mode Ⅱ crack with the crack growth
图 10 界面参数对Ⅱ型裂纹黏聚区长度的影响
Figure 10. Influences of interface parameters on the cohesive zone length of the mode Ⅱ crack
mechanical properties of the HTA6376/C composite single layer plate $ {E_{11}} $=120 GPa ${E_{22}} = {E_{33}}$=10.5 GPa $ {G_{12}} = {G_{13}} $=5.25 GPa $ {G_{23}} $= 3.48 GPa ${\nu _{12}} = {\nu _{13}}$=0.3 ${\nu _{23}}$=0.51 fracture properties of the interfacial cohesive zone $ {G_{{\text{Ic}}}} $=0.26 N/mm GⅡc=1.002 N/mm $ {\sigma _{\text{c}}} $=30 MPa $ {\tau _{\text{c}}} $=60 MPa $ K_{\rm{nn}}^{{\text{initial}}} $=1 × 103 GPa/mm $ K_{\rm{ss}}^{{\text{initial}}} $=1 × 103 GPa/mm 
下载: 导出CSV
-
[1] 赵丽滨, 龚愉, 张建宇. 纤维增强复合材料层合板分层扩展行为研究进展[J]. 航空学报, 2019, 40(1): 522509. (ZHAO Libin, GONG Yu, ZHANG Jianyu. A survey on delamination growth behavior in fiber reinforced composite laminates[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(1): 522509.(in Chinese) [2] 姚辽军, 赵美英, 万小朋. 基于CDM-CZM的复合材料补片补强参数分析[J]. 航空学报, 2012, 33(4): 666-671. (YAO Liaojun, ZHAO Meiying, WAN Xiaopeng. Parameter analysis of composite laminates with patched reinforcement based on CDM-CZM[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(4): 666-671.(in Chinese) [3] BENNATI S, FISICARO P, VALVO P S. An enhanced beam-theory model of the mixed-mode bending (MMB) test, part Ⅰ: literature review and mechanical model[J]. Meccanica, 2013, 48(2): 443-462. doi: 10.1007/s11012-012-9686-3 [4] BENNATI S, FISICARO P, VALVO P S. An enhanced beam-theory model of the mixed-mode bending (MMB) test, part Ⅱ: applications and results[J]. Meccanica, 2013, 48(2): 465-484. doi: 10.1007/s11012-012-9682-7 [5] HASHEMI S, KINLOCH A, WILLIAMS J. The analysis of interlaminar fracture in uniaxial fibre-polymer composites[J]. Proceedings of the Royal Society of London, 1990, 427(1872): 173-199. [6] CARLSSON L, GILLESPIE J, PIPES R. On the analysis and design of the end notched flexure (ENF) specimen for mode Ⅱ testing[J]. Journal of Composite Materials, 1986, 20(6): 594-604. doi: 10.1177/002199838602000606 [7] FAN C, JAR P, CHENG J. Revisit the analysis of end-notched-flexure (ENF) specimen[J]. Composites Science and Technology, 2006, 66(10): 1497-1498. doi: 10.1016/j.compscitech.2006.01.016 [8] VALVO P S. Does shear deformability influence the mode Ⅱ delamination of laminated beams?[C]//17th European Conference on Fracture(ECF17). 2008. [9] WHITNEY J, GILLESPIE J, CARLSSON L. Singularity approach to the analysis of the end notch flexure specimen[C]//American Society for Composites Second Technical Conference. 1987: 391-398. [10] WHITNEY J. Analysis of interlaminar mode Ⅱ bending specimens using a higher order beam theory[J]. Journal of Reinforced Plastics and Composites, 1990, 9(6): 522-536. doi: 10.1177/073168449000900601 [11] WILLIAMS J. End corrections for orthotropic DCB specimens[J]. Composites Science and Technology, 1989, 35(4): 367-376. doi: 10.1016/0266-3538(89)90058-4 [12] 陈瑛, 乔丕忠. 4ENF黏聚解析模型分析[J]. 河海大学学报(自然科学版), 2008, 36(2): 234-237. (CHEN Ying, QIAO Pizhong. Cohesive analytic model of 4ENF specimen[J]. Journal of Hohai University (Natural Sciences) , 2008, 36(2): 234-237.(in Chinese) [13] 刘伟先, 周光明, 王新峰. 复合材料ENF试件裂纹扩展理论分析[J]. 航空学报, 2014, 35(1): 187-194. (LIU Weixian, ZHOU Guangming, WANG Xinfeng. Theoretical analysis of crack propagation of composite ENF specimens[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 187-194.(in Chinese) [14] REDDY J. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis[M]. CRC Press, 2004. [15] PARK K, PAULINO G. Cohesive zone models: a critical review of traction-separation relationships across fracture surfaces[J]. Applied Mechanics Reviews, 2011, 64(6): 060802. doi: 10.1115/1.4023110 [16] HARPER P, HALLETT S. Cohesive zone length in numerical simulations of composite delamination[J]. Engineering Fracture Mechanics, 2008, 75(16): 4774-4792. doi: 10.1016/j.engfracmech.2008.06.004 -
计量
- 文章访问数: 638
- HTML全文浏览量: 252
- PDF下载量: 46
- 被引次数: 0
渝公网安备50010802005915号