含源项双曲守恒方程的保平衡HLL格式

彭国良; 王仲琦; 张俊杰; 任泽平; 谢海燕; 杜太焦

doi:10.21656/1000-0887.430084

含源项双曲守恒方程的保平衡HLL格式

doi: 10.21656/1000-0887.430084

1.
北京理工大学机电学院，北京 100081
2.
西北核技术研究所，西安 710024

详细信息

作者简介:
彭国良（1985—），男，副研究员（通讯作者. E-mail：pengguoliang@nint.ac.cn）

中图分类号: O35
计量
- 文章访问数: 498
- HTML全文浏览量: 270
- PDF下载量: 91
- 被引次数: 0
出版历程
- 收稿日期: 2022-03-15
- 录用日期: 2022-07-01
- 修回日期: 2022-06-09
- 网络出版日期: 2022-12-27
- 刊出日期: 2023-01-01

A Well-Balanced HLL Scheme for Hyperbolic Conservation Systems With Source Terms

1.
School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, P.R.China
2.
Northwest Institute of Nuclear Technology, Xi’an 710024, P.R.China

摘要

摘要:
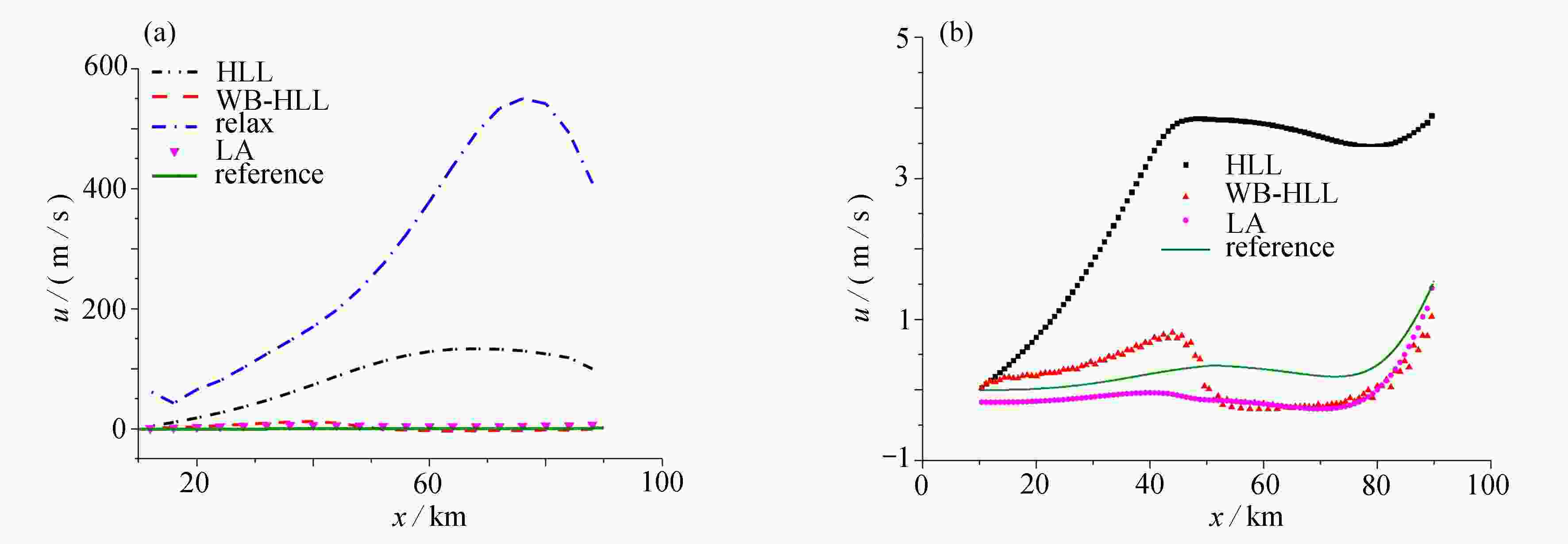
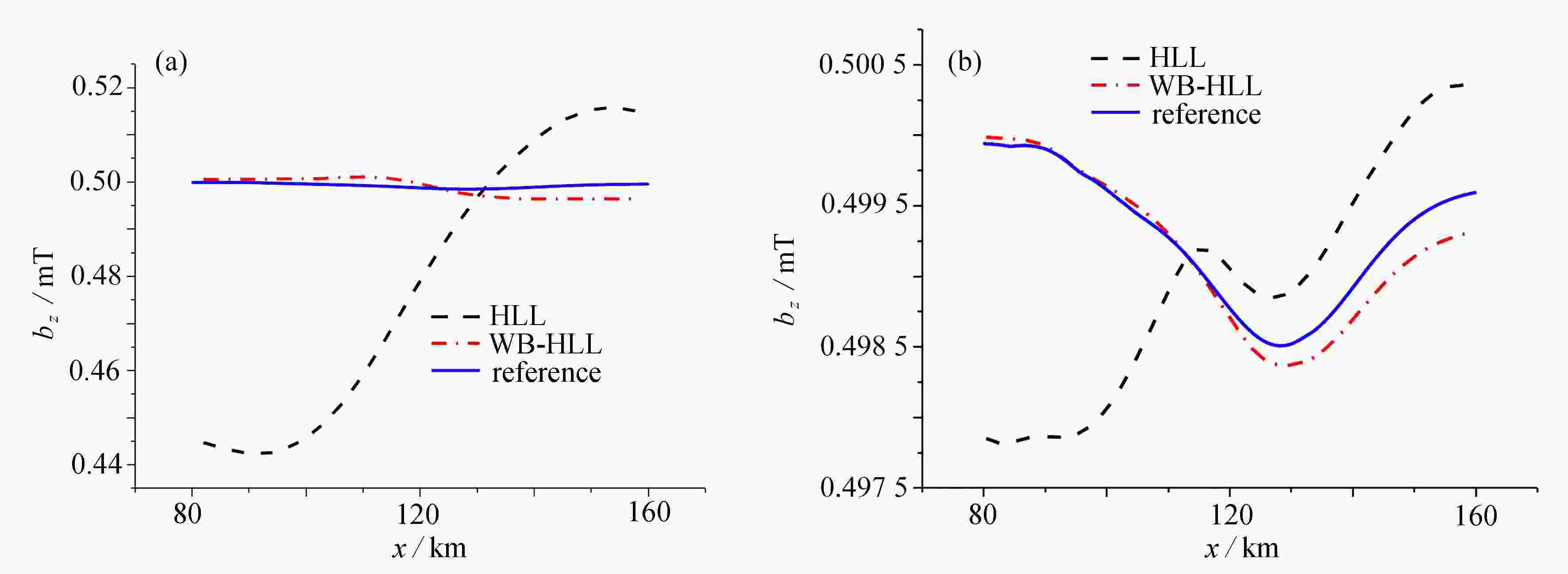
针对含源项的双曲守恒方程给出了一种新的有限体积格式。经典的有限体积格式不能正确地模拟对流通量项和外力之间的平衡所产生的动力学问题。为解决这个问题，仿照经典的HLL近似Riemann求解器设计思路设计了含源项的近似Riemann求解器。针对含重力源项的一维流体Euler方程和理想磁流体方程，通过对通量计算格式的修正得到了保平衡HLL格式（WB-HLL），并给出了保平衡的证明。针对一维Euler方程和理想磁流体给出了两个算例，比较了传统HLL格式和提出的WB-HLL格式的计算精度。计算结果表明，WB-HLL格式精度更高，收敛更快。
- 双曲守恒方程 /
- 源项 /
- 近似Riemann求解器 /
- 保平衡格式 /
- 有限体积方法
Abstract:
A new finite volume scheme was proposed for hyperbolic conservation systems with source terms. The classical finite volume schemes could not accurately simulate the dynamic problems caused by the balance between flux terms and source terms. To deal with this problem, an approximate Riemann solver with source terms was designed in accordance with the classical HLL approximate Riemann solver. The well-balanced HLL scheme (WB-HLL) was obtained through modification of the flux calculation schemes for 1D Euler equations and ideal MHD equations with gravity source terms, and a proof for the well-balanced property of the new scheme was presented. Two numerical examples of 1D Euler equations and ideal MHD equations demonstrate that the proposed WB-HLL scheme has higher accuracy and faster convergence than the classical HLL ones.
- hyperbolic conservation system /
- source term /
- approximate Riemann solver /
- well-balanced HLL scheme /
- finite volume scheme

HTML全文

图 1 HLL近似Riemann解示意图

Figure 1. The sketch of HLL approximate Riemann solvers

下载: 全尺寸图片幻灯片

图 2 不同格式计算的流体扰动速度：(a) 网格数N=20；(b) 网格数N=100

Figure 2. Fluid perturbed velocities with different schemes: (a) grid number N=20; (b) grid number N=100

下载: 全尺寸图片幻灯片

图 3 不同格式计算的磁流体扰动速度：(a) 网格数N=20；(b) 网格数N=100

Figure 3. MHD perturbed velocities with different schemes: (a) grid number N=20; (b) grid number N=100

下载: 全尺寸图片幻灯片

图 4 不同格式计算的磁流体磁场：(a) 网格数N=20；(b) 网格数N=100

Figure 4. MHD magnetic results with different schemes: (a) grid number N=20; (b) grid number N=100

下载: 全尺寸图片幻灯片

参考文献(14)

[1]	CHALONS C, GIRARDIN M, KOKH S. Large time step asymptotic preserving numerical schemes for the gas dynamics equations with source terms[J]. SIAM Journal on Scientific Computing, 2003, 35(6): A2874-A2902.
[2]	LIANG Q, MARCHE F. Numerical resolution of well-balanced shallow water equations with complex source terms[J]. Advances in Water Resources, 2009, 32: 873-884. doi: 10.1016/j.advwatres.2009.02.010
[3]	DESVEAUXV, ZENK M, BERTHON C, et al. A Well-Balanced Scheme for the Euler Equations With a Gravitational Potential[M]//Finite Volumes for Complex Applications Ⅶ: Methods and Theoretical Aspects Springer Proceedings in Mathematics and Statistics. Springer, 2014, 77: 217-226.
[4]	GHITTI B, BERTHON C, LE M H, et al. A fully well-balanced scheme for the 1D blood flow equations with friction source term[J]. Journal of Computational Physics, 2020, 421: 109750. doi: 10.1016/j.jcp.2020.109750
[5]	CUI S. Well-balanced central upwind schemes[D]. PhD Thesis. New Orleans, LA: Tulane University, 2015.
[6]	OZCAN S N. Development of well-balanced and asymptotic preserving numerical methods for partial differential equations[D]. PhD Thesis. Raleigh, NC: North Carolina State University, 2017.
[7]	CHALONS C, COQUELF, GODLEWSKI E, et al. Godunov-type schemes for hyperbolic systems with parameter-dependent source: the case of Euler system with friction[J]. Mathematical Models and Methods in Applied Sciences, 2010, 11(20): 2109-2166.
[8]	FRANCK E, MENDOZA L S. Finite volume scheme with local high order discretization of the hydrostatic equilibrium for the Euler equations with external forces[J]. Journal of Scientific Computing, 2016, 69: 314-354.
[9]	HARTENA, LAX P D, LEER V B. On upstream differencing and Godunov-type schemes for hyperbolic conservation laws[J]. SIAM Review, 1983, 25: 53-79.
[10]	胡立军, 袁礼. 一种基于TV分裂的真正多维Riemann解法器[J]. 应用数学和力学, 2017, 38(3): 243-264 HU Lijun, YUAN Li. A genuinely multidimensional Riemann solver based on the TV splitting[J]. Applied Mathematics and Mechanics, 2017, 38(3): 243-264.(in Chinese)
[11]	郑素佩, 李霄, 赵青宇, 等. 求解二维浅水波方程的旋转混合格式[J]. 应用数学和力学, 2022, 43(2): 176-186 ZHENG Supei, LI Xiao, ZHAO Qingyu, et al. A rotated mixed scheme for solving 2D shallow water equations[J]. Applied Mathematics and Mechanics, 2022, 43(2): 176-186.(in Chinese)
[12]	TORO E F. Riemann Solvers and Numerical Methods for Fluid Dynamics: a Practical Introduction[M]. New York: Springer, 1999.
[13]	MIGNONE A. High-order conservative reconstruction schemes for finite volume methods in cylindrical and spherical coordinates[J]. Journal of Computational Physics, 2014, 270: 784-820. doi: 10.1016/j.jcp.2014.04.001
[14]	ZINGALE M, DURSI L J, ZUHONE J, et al. Mapping initial hydrostatic models in Godunov codes[J]. The Astrophysical Journal Supplement Series, 2002, 143: 539-565.