一维六方压电准晶双材料界面共线裂纹问题

卢绍楠; 赵雪芬; 马园园

doi:10.21656/1000-0887.430111

一维六方压电准晶双材料界面共线裂纹问题

doi: 10.21656/1000-0887.430111

1.
宁夏大学数学统计学院, 银川 750021
2.
宁夏大学新华学院, 银川 750021

基金项目:

国家自然科学基金项目 12062021

宁夏自然科学基金项目 2022AAC03013

详细信息

作者简介:
卢绍楠(2000—), 女, 硕士生(E-mail: 1936136502@qq.com)

通讯作者:
赵雪芬(1983—), 女, 副教授, 博士, 硕士生导师(通讯作者. E-mail: snownfen@163.com)

中图分类号: O343.8
计量
- 文章访问数: 534
- HTML全文浏览量: 205
- PDF下载量: 58
- 被引次数: 0
出版历程
- 收稿日期: 2022-03-31
- 修回日期: 2022-06-28
- 刊出日期: 2023-07-01

Research on Interfacial Collinear Cracks Between 1D Hexagonal Piezoelectric Quasicrystal Bimaterials

1.
School of Mathematics and Statistics, Ningxia University, Yinchuan 750021, P.R.China
2.
Xinhua College, Ningxia University, Yinchuan 750021, P.R.China

摘要

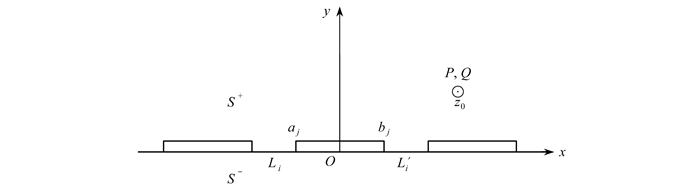
摘要: 利用复变函数理论中的解析延拓、奇性主部分析和推广的Liouville定理, 求解了一维六方压电准晶双材料在集中载荷作用下界面共线裂纹反平面弹性问题. 导出了含有一条和两条有限长界面裂纹的封闭解, 同时给出了裂纹尖端场强度因子(包含声子场和相位子场应力强度因子和电位移强度因子)的表达式. 数值算例分析了外荷载与耦合系数之比对裂纹尖端场强度因子变化规律的影响. 从数值结果中可以看出, 当裂纹长度增加时，裂纹尖端场强度因子随之增加; 应力强度因子随双材料耦合系数之比的增大而增大, 电位移强度因子几乎不变; 不同载荷作用下，裂纹尖端场强度因子随着裂纹长度改变时的变化趋势也不尽相同. 研究结果可为压电准晶双材料的设计和制备提供一定的理论参考.
- 一维六方压电准晶双材料 /
- 界面共线裂纹 /
- 复变函数方法 /
- 场强度因子
Abstract: By means of the analytic continuation, the singularity principal part analysis and the extended Liouville theorem in the complex function theory, the anti-plane elastic problem of interfacial collinear cracks between 1D hexagonal piezoelectric quasicrystal bimaterials under concentrated loads, was addressed. The closed solutions for biomaterial interface containing 1 and 2 finite-length cracks under concentrated loads were derived. At the same time, the crack tip field intensity factors (including the phonon field, the phason field stress intensity factors and the electric displacement intensity factor) were given. The effects of the ratio of the external load to the coupling coefficient on the intensity factor variation of the crack tip field were analyzed by numerical examples. The numerical results show that, the intensity factor of the crack tip field increases with the crack length and with the ratio of coupling coefficients, while the electric displacement intensity factor keeps almost unchanged. The field intensity factor of the crack tip varies with the crack length in different styles under different loads. The research results provide a theoretical reference for the design and preparation of piezoelectric quasicrystals.
- 1D hexagonal piezoelectric quasicrystal bimaterial /
- interfacial collinear crack /
- complex function method /
- field strength factor

HTML全文

图 1 集中载荷作用于含共线界面裂纹的一维六方压电准晶双材料

Figure 1. A 1D hexagonal piezoelectric quasicrystal bimaterial with collinear interfacial cracks under a concentrated load

下载: 全尺寸图片幻灯片

图 2 集中载荷作用在含一条界面裂纹的压电准晶双材料

Figure 2. A piezoelectric quasicrystal bimaterial with an interfacial crack subjected to a concentrated load

下载: 全尺寸图片幻灯片

图 3 集中载荷作用在含两条界面裂纹的压电准晶双材料

Figure 3. A piezoelectric quasicrystal bimaterial with 2 interfacial cracks subjected to a concentrated load

下载: 全尺寸图片幻灯片

图 4 单个界面裂纹面上受集中载荷

Figure 4. single interfacial crack surface subjected to a concentrated load

下载: 全尺寸图片幻灯片

图 5 单个界面裂纹面上受均布集中载荷

Figure 5. A single interfacial crack surface subjected to uniformly distributed concentrated loads

下载: 全尺寸图片幻灯片

图 6 集中载荷作用在界面裂纹面

Figure 6. A concentrated load applied to the interface crack surface

下载: 全尺寸图片幻灯片

图 7 R₃⁽²⁾/R₃⁽¹⁾不同时, K_Ⅲ^σ随l变化

Figure 7. The variation of K_Ⅲ^σ with l for different R₃⁽²⁾/R₃⁽¹⁾ values

下载: 全尺寸图片幻灯片

图 8 R₃⁽²⁾/R₃⁽¹⁾不同时, K_Ⅲ^H随l变化

Figure 8. The variation of K_Ⅲ^H with l for different R₃⁽²⁾/R₃⁽¹⁾ values

下载: 全尺寸图片幻灯片

图 9 R₃⁽²⁾/R₃⁽¹⁾不同时, K_Ⅲ^D随l变化

Figure 9. The variation of K_Ⅲ^Dwith l for different R₃⁽²⁾/R₃⁽¹⁾ values

下载: 全尺寸图片幻灯片

图 10 P₁不同时, K_Ⅲ^σ随l变化

Figure 10. The variation of K_Ⅲ^σ with l for different P₁ values

下载: 全尺寸图片幻灯片

图 11 P₁不同时, K_Ⅲ^H随l变化

Figure 11. The variation of K_Ⅲ^H with l for different P₁ values

下载: 全尺寸图片幻灯片

图 12 P₁不同时, K_Ⅲ^D随l变化

Figure 12. The variation of K_Ⅲ^D with l for different P₁ values

下载: 全尺寸图片幻灯片

图 13 P₂不同时, K_Ⅲ^σ随l变化

Figure 13. The variation of K_Ⅲ^σ with l for different P₂ values

下载: 全尺寸图片幻灯片

图 14 P₂不同时, K_Ⅲ^H随l变化

Figure 14. The variation of K_Ⅲ^H with l for different P₂ values

下载: 全尺寸图片幻灯片

图 15 P₂不同时, K_Ⅲ^D随l变化

Figure 15. The variation of K_Ⅲ^D with l for different P₂ values

下载: 全尺寸图片幻灯片

图 16 Q不同时, K_Ⅲ^σ随l变化

Figure 16. The variation of K_Ⅲ^σ with l for different Q values

下载: 全尺寸图片幻灯片

图 17 Q不同时, K_Ⅲ^H随l变化

Figure 17. The variation of K_Ⅲ^H with l for different Q values

下载: 全尺寸图片幻灯片

图 18 Q不同时, K_Ⅲ^D随l变化

Figure 18. The variation of K_Ⅲ^D with l for different Q values

下载: 全尺寸图片幻灯片

表 1 一维六方压电准晶双材料弹性常数

Table 1. Elastic constants of 1D hexagonal piezoelectric quasicrystals

material	C₄₄/GPa	K₂/GPa	R₃/GPa	e₁₅¹/(C·m^-2)	e₁₅²/(C·m^-2)	$ \epsilon_{11}$/(10^-9 C²·N^-1·m^-2)
1	70.19	24	0.884 6	11.6	1.16	5
2	50	0.3	1.2	-0.318	-0.16	0.082 6

下载: 导出CSV

参考文献(21)

[1]	SHECHTMAN D, BLECH I, GRATIAS D, et al. Metallic phase with long-range orientational order and no translational symmetry[J]. Physical Review Letters, 1984, 53(20): 1951-1953. doi: 10.1103/PhysRevLett.53.1951
[2]	ZHANG Z, URBAN K. Transmission electron microscope observations of dislocations and stacking faults in a decagonal Al-Cu-Co alloy[J]. Philosophical Magazine Letters, 1989, 60(3): 97-102. doi: 10.1080/09500838908206442
[3]	苏梦雨, 肖俊华, 冯国益. 一维六方准晶中纳米尺度开裂孔洞的Ⅲ型断裂力学[J]. 固体力学学报, 2020, 41(3): 281-292. https://www.cnki.com.cn/Article/CJFDTOTAL-GTLX202003011.htm SU Mengyu, XIAO Junhua, FENG Guoyi. Type Ⅲ fracture mechanics of a nanoscale cracked hole in one-dimensional hexagonal quasicrystals[J]. Chinese Journal of Solid Mechanics, 2020, 41(3): 281-292. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GTLX202003011.htm
[4]	CHENG J X, SHENG D, SHI P P. Fracture analysis of one-dimensional hexagonal quasicrystals: researches of a finite dimensional rectangular plate by boundary collocation method[J]. Journal of Mechanical Science and Technology, 2017, 31(5): 2373-2383. doi: 10.1007/s12206-017-0434-4
[5]	张炳彩, 丁生虎, 张来萍. 一维六方准晶双材料中圆孔边共线界面裂纹的反平面问题[J]. 应用数学和力学, 2022, 43(6): 639-647. doi: 10.21656/1000-0887.420202 ZHANG Bingcai, DING Shenghu, ZHANG Laiping. The anti-plane problem of collinear interface cracks emanating from a circular hole in 1D hexagonal quasicrystal bi-materials[J]. Applied Mathematics and Mechanics, 2022, 43(6): 639-647. (in Chinese) doi: 10.21656/1000-0887.420202
[6]	SU M Y, XIAO J H, FENG G Y, et al. Mode-Ⅲ fracture of a nanoscale cracked hole in one-dimensional hexagonal piezoelectric quasicrystals[J]. International Journal of Mechanics and Materials in Design, 2022, 18: 423-433. doi: 10.1007/s10999-022-09589-7
[7]	RADI E, MARIANO P M. Stationary straight cracks in quasicrystals[J]. International Journal of Fracture, 2010, 166(1/2): 105-120.
[8]	高媛媛, 刘官厅. 一维正交准晶中具有四条裂纹的椭圆孔口问题的解析解[J]. 应用数学和力学, 2019, 40(2): 210-222. doi: 10.21656/1000-0887.390032 GAO Yuanyuan, LIU Guanting. Analytical solutions to problems of elliptical holes with 4 edge cracks in 1D orthorhombic quasicrystals[J]. Applied Mathematics and Mechanics, 2019, 40(2): 210-222. (in Chinese) doi: 10.21656/1000-0887.390032
[9]	YANG J, ZHOU Y T, MA H L, et al. The fracture behavior of two asymmetrical limited permeable cracks emanating from an elliptical hole in one-dimensional hexagonal quasicrystals with piezoelectric effect[J]. International Journal of Solids and Structures, 2017, 108: 175-185. doi: 10.1016/j.ijsolstr.2016.12.012
[10]	HU K Q, JIN H, YANG Z J, et al. Interface crack between dissimilar one-dimensional hexagonal quasicrystals with piezoelectric effect[J]. Acta Mechanica, 2019, 230: 2455-2474. doi: 10.1007/s00707-019-02404-z
[11]	ZHOU Y B, LI X F. Fracture analysis of an infinite 1D hexagonal piezoelectric quasicrystal plate with a penny-shaped dielectric crack[J]. European Journal of Mechanics A: Solids, 2019, 76: 224-234. doi: 10.1016/j.euromechsol.2019.04.011
[12]	ZHOU Y B, LI X F. A Yoffe-type moving crack in one-dimensional hexagonal piezoelectric quasicrystals[J]. Applied Mathematical Modelling, 2019, 65: 148-163.
[13]	刘兴伟, 李星, 汪文帅. 一维六方压电准晶中正n边形孔边裂纹的反平面问题[J]. 应用数学和力学, 2020, 41(7): 713-724. doi: 10.21656/1000-0887.400334 LIU Xingwei, LI Xing, WANG Wenshuai. The anti-plane problem of regular n-polygon holes with radial edge cracks in 1D hexagonal piezoelectric quasicrystals[J]. Applied Mathematics and Mechanics, 2020, 41(7): 713-724. (in Chinese) doi: 10.21656/1000-0887.400334
[14]	ALATY G, DÖMECI M C. On the fundamental equations of piezoelectric of quasicrystal media[J]. International Journal of Solids and Structures, 2012, 49(23/24): 3255-3262.
[15]	路见可. 平面弹性复变方法[M]. 武汉: 武汉大学出版社, 2002. LU Jianke. Complex Variable Method of Plane Elasticity[M]. Wuhan: Wuhan University Press, 2002. (in Chinese)
[16]	樊大钧. 数学弹性力学[M]. 北京: 新时代出版社, 1983. FAN Danjun. Mathematical Elasticity[M]. Beijing: New Era Press, 1983. (in Chinese)
[17]	钟玉泉. 复变函数[M]. 北京: 高等教育出版社, 1987. ZHONG Yuquan. Complex Variables Functions[M]. Beijing: Higher Education Press, 1987. (in Chinese)
[18]	范天佑. 准晶数学弹性理论及应用[M]. 北京: 北京理工大学出版社, 1999. FAN Tianyou. Mathematical Theory of Elasticity of Quasicrystals and Its Applications[M]. Beijing: Beijing Institute of Technology Press, 1999. (in Chinese)
[19]	DANG H Y, ZHAO M H, FAN C Y, et al. Analysis of a three-dimensional arbitrarily shaped interface crack in a one-dimensional hexagonal thermo-electro-elastic quasicrystal bi-material, part 2: numerical method[J]. Engineering Facture Mechanics, 2017, 180: 268-281.
[20]	LI L H, ZHAO Y. Interaction of a screw dislocation with interface and wedge-shaped cracks in one-dimensional hexagonal piezoelectric quasicrystals bimaterial[J]. Mathematical Problems in Engineering, 2019, 2019: 1-7.
[21]	LANDAU L D, LIFSHITZ I E. Statistical Physics[M]. 2nd ed. New York: Pergaman Press, 1968.