基于联合观测与前馈补偿的四旋翼无人机自抗扰控制

肖友刚; 童俊豪

doi:10.21656/1000-0887.430135

基于联合观测与前馈补偿的四旋翼无人机自抗扰控制

doi: 10.21656/1000-0887.430135

肖友刚^,,
童俊豪

中南大学交通运输工程学院，长沙 410075

基金项目: 湖南省自然科学基金(2021JJ30847)

详细信息

作者简介:
肖友刚（1970—），男，教授，博士（通讯作者. E-mail：csuxyg@163.com）

中图分类号: TP273
计量
- 文章访问数: 675
- HTML全文浏览量: 235
- PDF下载量: 98
- 被引次数: 0
出版历程
- 收稿日期: 2022-04-18
- 修回日期: 2023-03-23
- 网络出版日期: 2023-03-25
- 刊出日期: 2023-03-15

Active Disturbance Rejection Control of Quadrotor UAVs Based on Joint Observation and Feedforward Compensation

XIAO Yougang^,,
TONG Junhao

School of Traffic and Transportation Engineering, Central South University, Changsha 410075, P.R.China

摘要

摘要:
为解决模型参数不确定与外界干扰影响下，四旋翼无人机飞控作业中姿态与轨迹跟踪精度下降，反应迟缓的问题，利用拓展Kalman滤波应对非线性系统问题出色的适应能力和噪声抑制能力，对四旋翼状态信息进行初步估算来抑制高频信号干扰，从而降低了扩张状态观测器的估计负担。同时，与扩张状态观测器联合估计由系统不确定性参数与外界扰动联合组成的“总扰动”，使系统对于精确模型的依赖性降低，并利用扰动估计的微分值进行前馈补偿，以提高对突变扰动的跟踪精度，克服了突变干扰下的相位滞后现象。综合联合观测器、带前馈补偿的LESO及带误差补偿的PD控制律，形成了一种利用拓展Kalman滤波与前馈补偿后的扩张状态观测器联合观测扰动，能较大程度抑制高频噪声和突变扰动的改进型自抗扰控制器。仿真与实验结果表明，联合观测器能有效地减小观测误差幅值且能超前校正观测相位滞后，从而更好地得到更精确的状态信息，改进型自抗扰控制器能更好地满足四旋翼飞行器快速反应、高效稳定的控制要求，精准高效地完成复杂轨迹跟踪。
- 四旋翼无人机 /
- 联合观测 /
- 拓展Kalman滤波 /
- 前馈补偿 /
- 改进型自抗扰
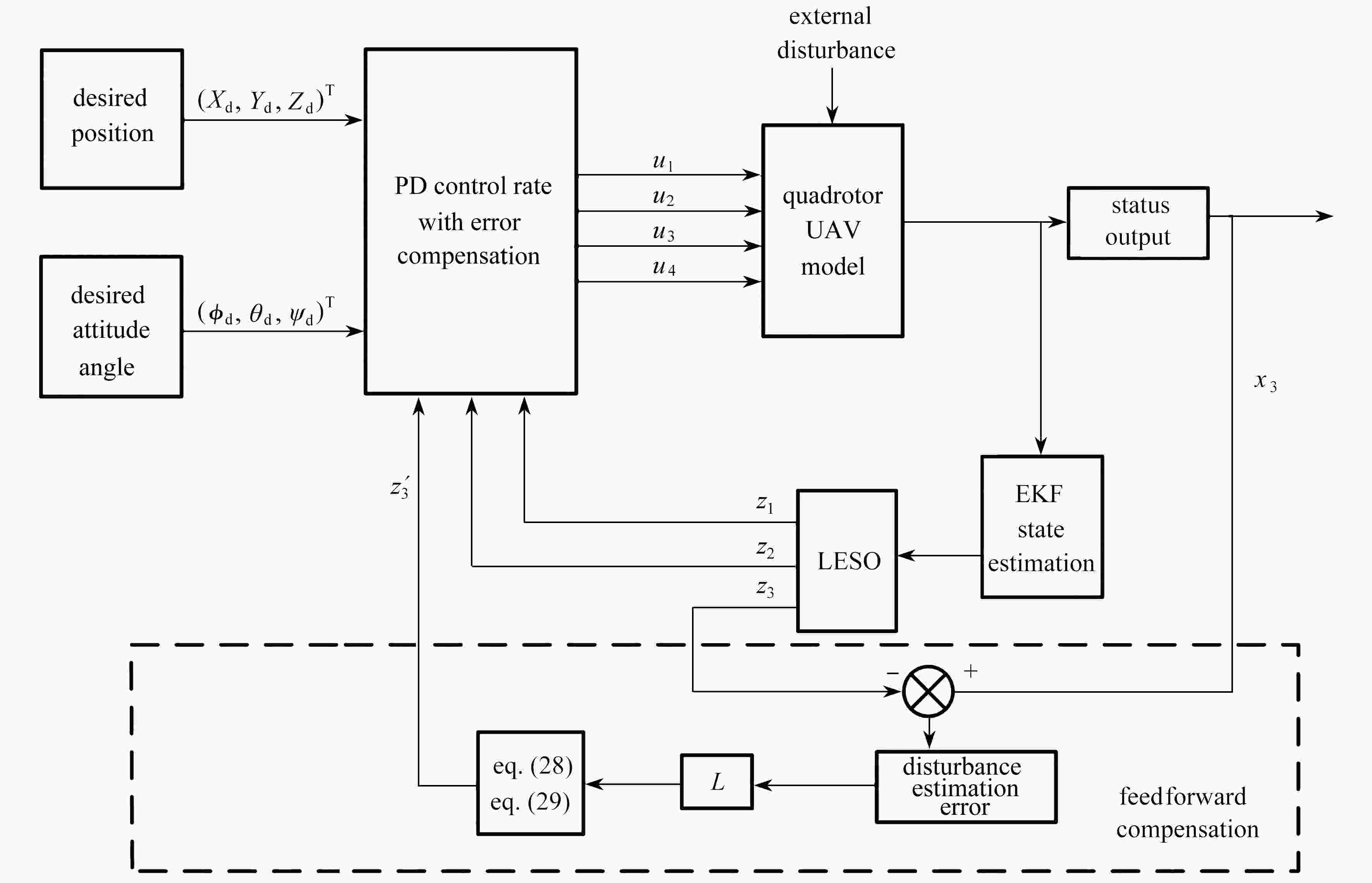
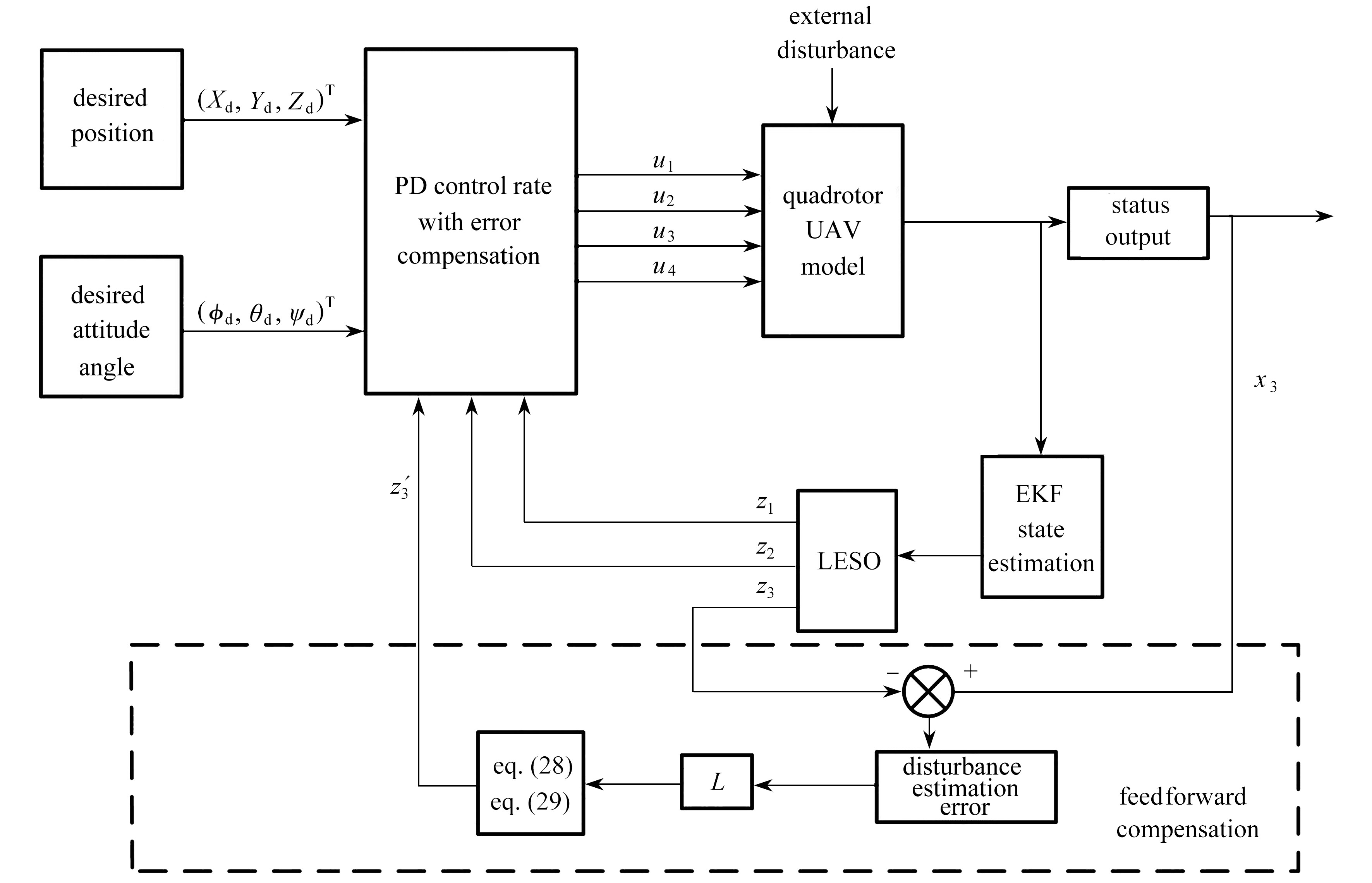
Abstract:
Under the effects of uncertain parameters and external disturbances, the attitude and trajectory tracking accuracy will be reduced and the response will be slowed down in the flight control of quadrotor unmanned air vehicles (UAVs). To solve this problem, the extended Kalman filter method was used given its excellent adaptability and noise suppression ability for nonlinear systems, to preliminarily estimate the quadrotor state information and suppress the high-frequency signal disturbance to reduce the estimation burden on the extended state observer. Moreover, the extended Kalman filter combined with the expanded state observer was applied to estimate the total disturbance composed of the system uncertainty parameters and external disturbances to reduce system reliance on precise models, and the differential values of the perturbation estimates were used for feedforward compensation to improve the tracking accuracy under abrupt disturbances and to overcome the phase lag caused by abrupt disturbances. The joint state observer, the linear extended state observer with feedforward compensation and the PD controller with error compensation were integrated to form an improved active disturbance rejection controller to jointly observe disturbances while suppressing high-frequency noises and abrupt disturbances to a relatively large extent, by means of the extended Kalman filter and the extended state observer with feedforward compensation. Simulation and experiment results show that, the joint observer can effectively reduce the observation error amplitude, correct the observation phase lag in advance and obtain more accurate state information, and the improved active disturbance rejection controller can better meet requirements of quadrotor UAVs for fast responses and stable control, and accurately and efficiently fulfill complex trajectory tracking tasks.
- quadrator UAV /
- joint observation /
- extended Kalman fliter /
- feedforward compensation /
- improved active disturbance rejection

HTML全文

图 1 改进型自抗扰控制系统流程

Figure 1. The flowchart for the IADRC system

下载: 全尺寸图片幻灯片

图 2 抗干扰与观测效果对比：(a) 位置与姿态角抗干扰效果对比；(b) COMO与LESO的观测效果对比

Figure 2. Comparisons of anti-interference and observation effects: (a) comparisons of anti-interference effects of the position and the attitude angle; (b) comparisons of observation effects of the COMO and the LESO

下载: 全尺寸图片幻灯片

图 3 四旋翼无人机飞行状态跟踪效果：(a)位置跟踪效果；(b)姿态角跟踪效果；(c)三维轨迹跟踪效果

Figure 3. Tracking effects of quadrotor UAV flight state: (a) tracking effects of the position; (b) tracking effects of the attitude angle; (c) tracking effects of the 3D trajectory

下载: 全尺寸图片幻灯片

图 4 四旋翼无人机实验台架

Figure 4. The test platform for the quadrotor UAV

下载: 全尺寸图片幻灯片

图 5 外部扰动下实验效果

Figure 5. Experimental effects by external disturbance

下载: 全尺寸图片幻灯片

表 1 EKF算法

Table 1. The EKF algorithm

stage	algorithm
starting condition	${{{\overset{\frown} {\boldsymbol{x}} }}_{\text{0}}} = E({{\boldsymbol{x}}_{\text{0}}}),{{\boldsymbol{P}}_{\text{0}}} = {{\rm{var}}} ({{\boldsymbol{x}}_{\text{0}}})$
time optimal estimate at step $k - 1$	${{\boldsymbol{\hat x}}_{k,k-1}} = {\boldsymbol{f}}({{\boldsymbol{\hat x}}_{k-1, k - 1}},{{\boldsymbol{u}}_k})$
prior covariance matrix	$\begin{gathered} { {\boldsymbol{P} }_{k,k-1} } = { {\rm{cov} } } ({ {\boldsymbol{x} }_k} - { { {\boldsymbol{\hat x} } }_{k,k-1} }) = { {\rm{cov} } } [{\boldsymbol{f} }({ {\boldsymbol{x} }_{k-1,k-1} },{ {\boldsymbol{u} }_{k-1} }) + { {\boldsymbol{\omega } }_k} - {\boldsymbol{f} }({ { {\boldsymbol{\hat x} } }_{k-1,k-1} },{ {\boldsymbol{u} }_{k-1} })] = \\ \qquad { {\boldsymbol{\varphi } }_{k,k-1} }{ {\boldsymbol{P} }_{k-1,k-1} }{\boldsymbol{\varphi } }_{ {\boldsymbol{k,k - 1} } }^{\text{T} } + { {\boldsymbol{\varGamma } }_{k,k-1} }{ {\boldsymbol{Q} }_k}{\boldsymbol{\varGamma } }_{k,k-1}^{\text{T} } \\ \end{gathered}$
Kalman gain	${ {\boldsymbol{K} }_k} = {{\boldsymbol{P}}_{k,k-1} }{\boldsymbol{H} }_k^{\text{T} }{[{ {\boldsymbol{H} }_k}{ {\boldsymbol{P} }_{k,k-1} }{\boldsymbol{H} }_k^{\text{T} } + { {\boldsymbol{R} }_k}]^{ - 1} }$
time optimal estimate at step $k$	${ {\boldsymbol{\hat x} }_{k,k} } = { {\boldsymbol{\hat x} }_{k,k-1} } + { {\boldsymbol{K} }_k}[{ {\boldsymbol{z} }_k} - {\boldsymbol{h} }({ {\boldsymbol{\hat x} }_{k,k-1} })]$
posterior covariance matrix	$\begin{gathered} { {\boldsymbol{P} }_{k,k} } = { {\rm{cov} } } ({ {\boldsymbol{x} }_k} - { { {\boldsymbol{\hat x} } }_{k,k} }) = { {\rm{cov} } } [({ {\boldsymbol{x} }_k} - { { {\boldsymbol{\hat x} } }_{k,k-1} }) - { {\boldsymbol{K} }_k}({\boldsymbol{h} }({ {\boldsymbol{x} }_k}) - {\boldsymbol{h} }({ { {\boldsymbol{\hat x} } }_{k,k-1} })) - { {\boldsymbol{K} }_k}{ {\boldsymbol{V} }_k}] = \\\qquad { {\rm{cov} } } [({ {\boldsymbol{x} }_k} - { { {\boldsymbol{\hat x} } }_{k,k-1} }) - { {\boldsymbol{K} }_k}({\boldsymbol{h} }({ {\boldsymbol{x} }_k}) - {\boldsymbol{h} }({ { {\boldsymbol{\hat x} } }_{k,k-1} }))] + { {\rm{cov} } } ({ {\boldsymbol{K} }_k}{ {\boldsymbol{V} }_k}) = ({\boldsymbol{I} } - { {\boldsymbol{K} }_k}{ {\boldsymbol{H} }_k}){ {\boldsymbol{P} }_{k,k-1} } \\ \end{gathered}$

下载: 导出CSV

表 2 IADRC和ADRC的性能对比

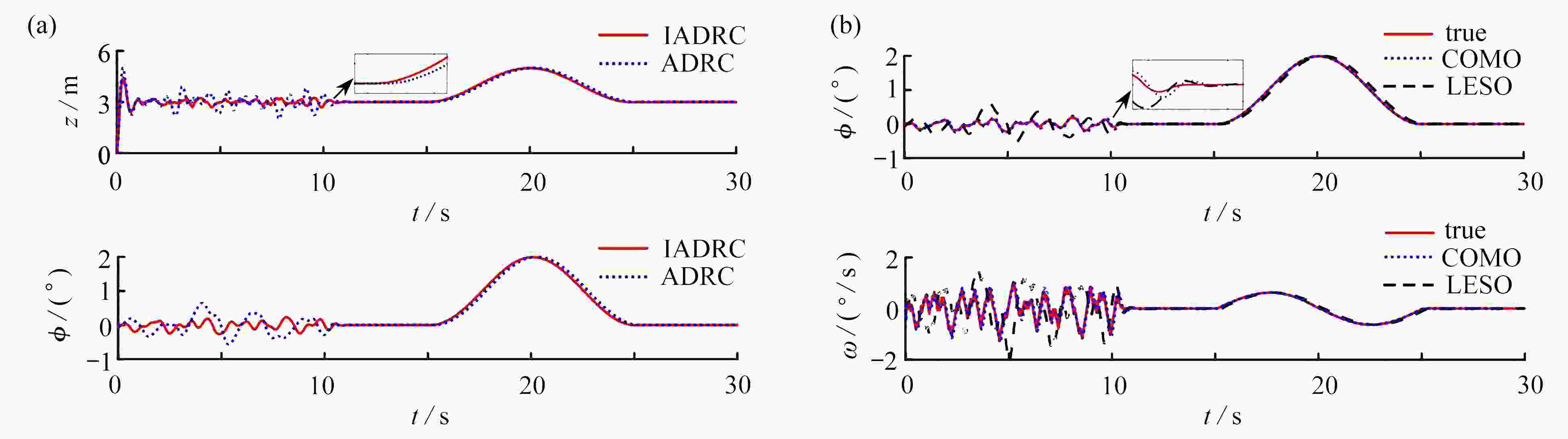
Table 2. Performance comparisons of the IADRC and the ADRC

	Z-channel maximum amplitude	Z-channel phase lag	$ \phi $-channel maximum amplitude	$ \phi $-channel phase lag
ADRC	5.02 m	0.24 s	0.65°	0.27 s
IADRC	4.42 m	0.10 s	0.24°	0.12 s

下载: 导出CSV

参考文献(22)

[1]	王芳, 高雅丽, 张政, 等. 输出误差约束下四旋翼无人机预定性能反步控制[J]. 控制与决策, 2021, 36(5): 1059-1068 doi: 10.13195/j.kzyjc.2019.1249 WANG Fang, GAO Yali, ZHANG Zheng, et al. Prescribed performance back-stepping control for quadrotor UAV with output error constraint[J]. Control and Decision, 2021, 36(5): 1059-1068.(in Chinese) doi: 10.13195/j.kzyjc.2019.1249
[2]	TANG P, ZHANG F, YE J, et al. An integral TSMC-based adaptive fault-tolerant control for quadrotor with external disturbances and parametric uncertainties[J]. Aerospace Science and Technology, 2020, 109: 106415.
[3]	LIANG X, FANG Y C, SUN N, et al. Nonlinear hierarchical control for unmanned quadrotor transportation systems[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3395-3405. doi: 10.1109/TIE.2017.2752139
[4]	LABBADI M, CHERKAOUI M. Robust adaptive nonsingular fast terminal sliding-mode tracking control for an uncertain quadrotor UAV subjected to disturbances[J]. ISA Transactions, 2020, 99: 290-304. doi: 10.1016/j.isatra.2019.10.012
[5]	GHADIRI H, EMAMI M, KHODADADI H. Adaptive super-twisting non-singular terminal sliding mode control for tracking of quadrotor with bounded disturbances[J]. Aerospace Science and Technology, 2021, 112: 106616. doi: 10.1016/j.ast.2021.106616
[6]	SHAO X, LIU J, WANG H. Robust back-stepping output feedback trajectory tracking for quadrotors via extended state observer and sigmoid tracking differentiator[J]. Mechanical Systems and Signal Processing, 2018, 104(5): 631-647.
[7]	LI Q, YUAN J P, ZHANG B. Extended state observer based output control for spacecraft rendezvous and docking with actuator saturation[J]. ISA Transactions, 2019, 88: 37-49. doi: 10.1016/j.isatra.2018.11.048
[8]	何绪飞, 艾剑良, 宋智桃. 多元数据融合在无人机结构健康监测中的应用[J]. 应用数学和力学, 2018, 39(4): 395-402 HE Xufei, AI Jianliang, SONG Zhitao. Application of multivariate data fusion in UAV structural health monitoring[J]. Applied Mathematics and Mechanics, 2018, 39(4): 395-402.(in Chinese)
[9]	肖友刚, 朱铖臻, 卢浩, 等. 一类欠驱动MIMO系统集中式自抗扰控制[J]. 应用数学和力学, 2020, 41(11): 1197-1209 XIAO Yougang, ZHU Chengzhen, LU Hao, et al. Centralized active disturbance rejection control for a class of underactuated MIMO systems[J]. Applied Mathematics and Mechanics, 2020, 41(11): 1197-1209.(in Chinese)
[10]	肖友刚, 卢浩, 王辉堤, 等. 一类非线性MIMO系统的自解耦控制[J]. 哈尔滨工业大学学报, 2020, 52(9): 129-136 XIAO Yougang, LU Hao, WANG Huidi, et al. Self-decoupling control for a class of nonlinear MIMO systems[J]. Journal of Harbin Institute of Technology, 2020, 52(9): 129-136.(in Chinese)
[11]	张勇, 陈增强, 张兴会, 等. 四旋翼无人机系统PD-ADRC串级控制[J]. 系统工程与电子技术, 2018, 40(9): 2055-2061. ZHANG Yong, CHEN Zengqiang, ZHANG Xinghui, et al. PD-ADRC cascade control for quadrotor system[J]. Systems Engineering and Electronics, 2018, 40(9): 2055-2061. (in Chinese)
[12]	章志诚. 基于ADRC的四旋翼飞行器自主避障控制系统研究[D]. 硕士学位论文. 杭州: 浙江大学, 2017. ZHANG Zhicheng. Research on autonomous obstacle avoidance control system of quadrotor based on ADRC[D]. Master Thesis. Hangzhou: Zhejiang University, 2017. (in Chinese)
[13]	石嘉, 裴忠才, 唐志勇, 等. 改进型自抗扰四旋翼无人机控制系统设计与实现[J]. 北京航空航天大学学报, 2021, 47(9): 1823-1831 doi: 10.13700/j.bh.1001-5965.2020.0333 SHI Jia, PEI Zhongcai, TANG Zhiyong, et al. Design and implementation of an improved auto-disturbance rejection quadrotor UAV control system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(9): 1823-1831.(in Chinese) doi: 10.13700/j.bh.1001-5965.2020.0333
[14]	胡丹丹, 张宇辰. 基于改进粒子群算法的四旋翼自抗扰控制器优化设计[J]. 计算机应用研究, 2019, 36(6): 1762-1766 HU Dandan, ZHANG Yuchen. Optimization design of quad-rotor auto-disturbance rejection controller based on improved particle swarm optimization[J]. Application Research of Computers, 2019, 36(6): 1762-1766.(in Chinese)
[15]	ZHANG Y, CHEN Z, ZHANG X. A novel control scheme for quadrotor UAV based upon active disturbance rejection control[J]. Aerospace Science and Technology, 2018, 79: 601-609. doi: 10.1016/j.ast.2018.06.017
[16]	刘祥, 童东兵, 陈巧玉. 基于观测器的非严格反馈时滞非线性系统的神经网络自适应控制[J]. 应用数学和力学, 2021, 42(6): 586-594 LIU Xiang, TONG Dongbing, CHEN Qiaoyu. Neural network adaptive control of non-strict feedback time-delay nonlinear systems based on observers[J]. Applied Mathematics and Mechanics, 2021, 42(6): 586-594.(in Chinese)
[17]	魏宇恒, 童东兵, 陈巧玉. 基于中间观测器的非线性系统的故障估计[J]. 应用数学和力学, 2021, 42(11): 1213-1220 WEI Yuheng, TONG Dongbing, CHEN Qiaoyu. Fault estimation of nonlinear systems based on intermediate observers[J]. Applied Mathematics and Mechanics, 2021, 42(11): 1213-1220.(in Chinese)
[18]	WANG X H, WANG W C. Nonlinear signal-correction observer and application to UAV navigation[J]. IEEE Transactions on Industrial Electronics, 2018, 66(6): 4600-4607.
[19]	BATTILOTTI S. Robust observer design under measurement noise with gain adaptation and saturated estimates[J]. Automatica, 2017, 81: 75-86. doi: 10.1016/j.automatica.2017.02.008
[20]	NAIR R R, BEHERA L. Robust adaptive gain higher order sliding mode observer based control-constrained nonlinear model predictive control for spacecraft formation flying[J]. IEEE/CAA Journal of Automatica Sinica, 2018, 5(1): 367-381. doi: 10.1109/JAS.2016.7510253
[21]	蔡文静. 基于等价输入干扰方法的四旋翼无人机扰动抑制与跟踪控制[D]. 博士学位论文. 北京: 中国地质大学, 2020. CAI Wenjing. Disturbance suppression and tracking control of quadrotor UAV based on equivalent input jamming method [D]. PhD Thesis. Beijing: China University of Geosciences, 2020. (in Chinese)
[22]	石喜玲. 多旋翼飞行器姿态测量及控制技术研究[D]. 博士学位论文. 太原: 中北大学, 2020. SHI Xiling. Research on attitude measurement and control technology of multi-rotor aircraft[D]. PhD Thesis. Taiyuan: North Central University, 2020. (in Chinese)