Numerical Simulation of the Quasi-2D Turbulence on a Half Soap Bubble Heated at the Bottom
-
摘要:
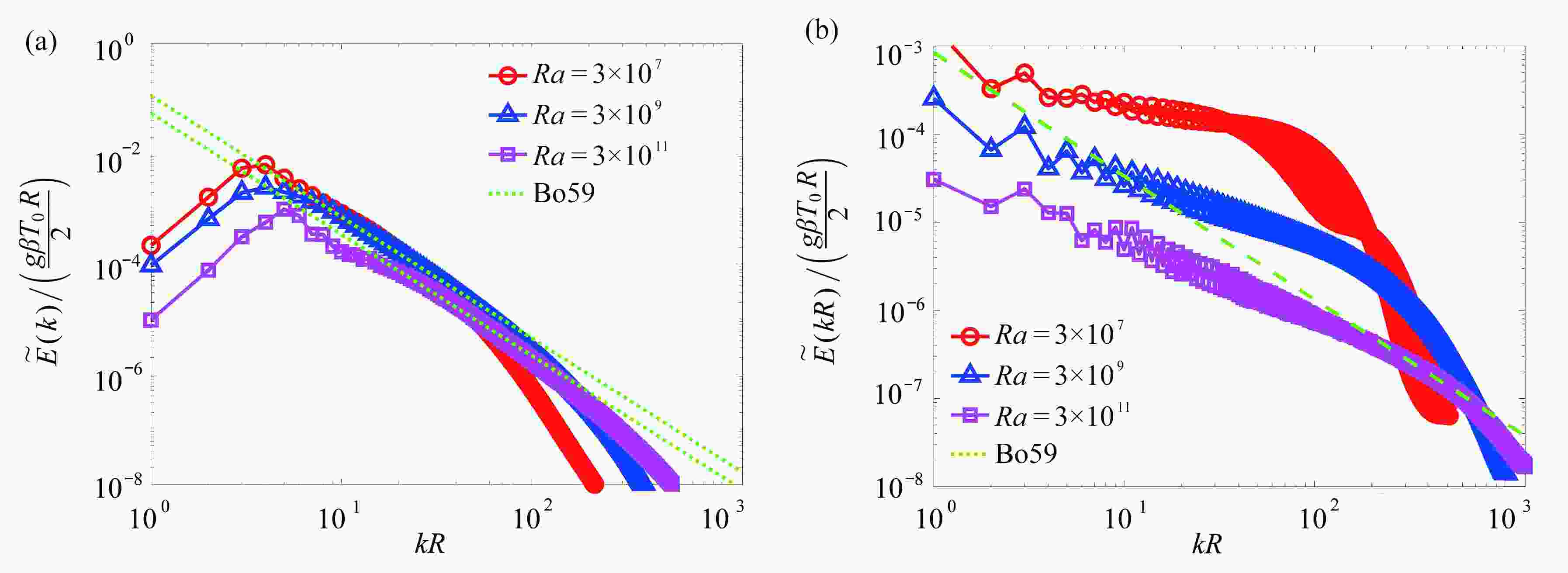
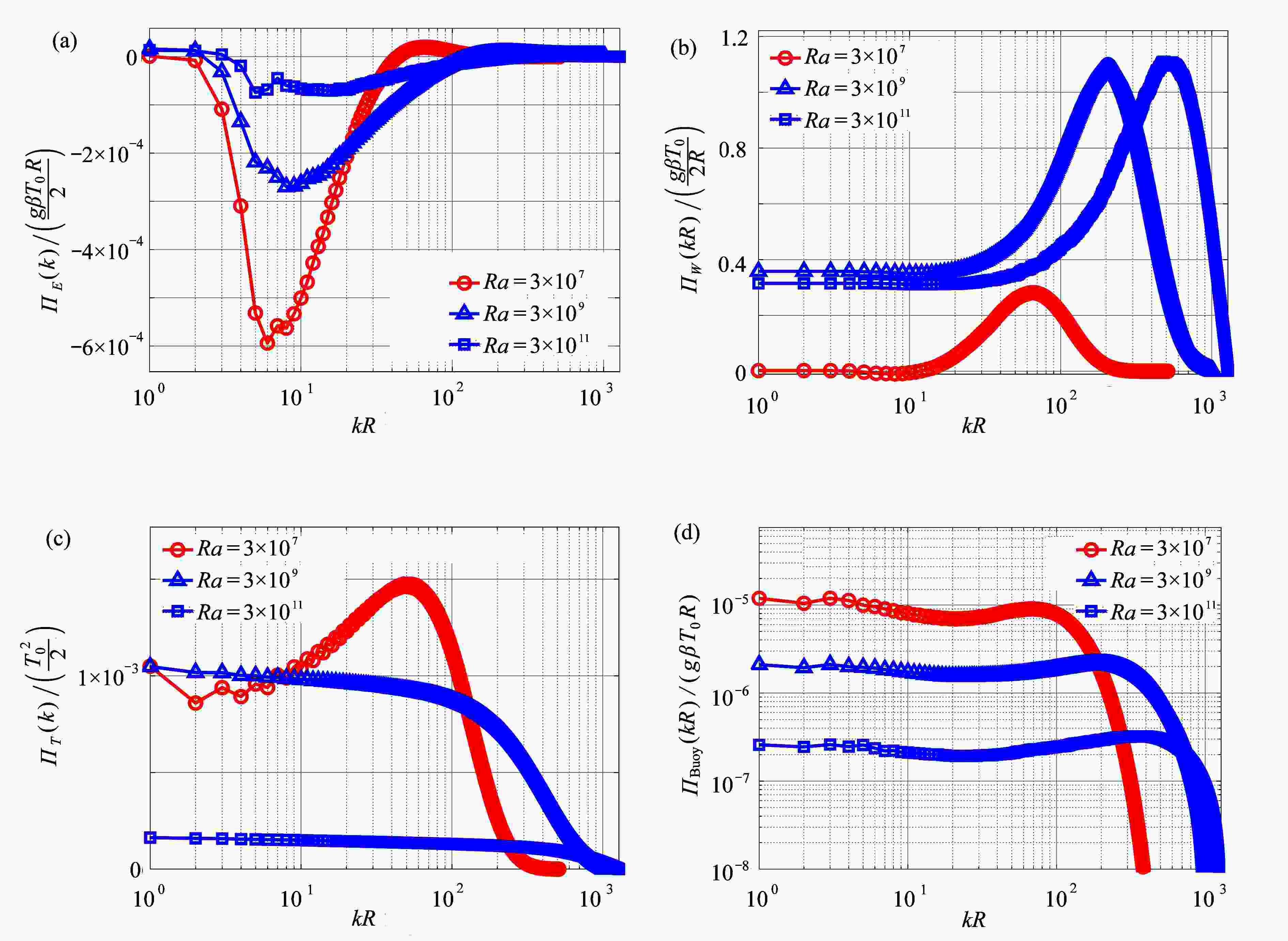
底部加热的肥皂泡是一种全新的二维热对流模型，在实验中已发现肥皂泡上的岛涡运动规律与飓风轨迹规律一致。然而，肥皂泡的曲面特征对其准二维流场的数值模拟以及数据分析造成了较多困难。针对肥皂泡球面几何特征，该文介绍了其直接数值模拟（DNS）方法，及其流场空间波数谱、湍流通量和结构函数的计算分析方法。开展了Ra=3×107，3×109，3×1011的数值计算，并获得了相应的波数谱、通量和湍流结构函数。计算结果表明，肥皂泡上速度的小尺度脉动特征满足Bo59的理论标度律，通过湍动能与拟涡能通量特征，发现在该准二维湍流场中存在湍流能量双级串现象。且随着Rayleigh数的增加，大尺度结构湍能量减小，更小尺度湍流结构能量增加。
Abstract:The soap bubble heated at the bottom was introduced as a novel quasi-2D turbulence system. The curved geometry of the bubble brings challenges for the direct numerical simulations (DNS) of the turbulence on the bubble. In order to overcome the difficulties due to the curved geometry, a numerical method based on the stereographic projection was implemented for the DNS of the soap bubble. The numerical methods to compute the spectrum, the flux and the structure functions of the flows on the bubble were described in detail. Three different Rayleigh numbers Ra=3×107，3×109，3×1011 were used in the simulation based on the present numerical methods. Then, the related spectrum, flux and structure functions were calculated. The results indicate that, both the inversed energy cascade and forward enstrophy cascade can be observed in all the calculation cases. The Bo59 scaling law fits the small-scale fluctuations on the soap bubble. With the increase of the Rayleigh number, the turbulent energy decreases for the large-scale plumes, and the kinetic energy increases for the higher wave number structures.
-
Key words:
- soap bubble /
- turbulence /
- structure function /
- direct numerical simulation
-
图 1 赤平极射投影法示意图
注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同。
Figure 1. An illustration of the stereographic projection
图 4 不同网格分辨率下，算例2的总拟涡能随时间的变化曲线（左）和拟涡能总量的统计值随网格分辨率变化曲线（右）
Figure 4. The temporal evolution of the total enstrophy on the bubble with different mesh resolutions (left) & the variation of the mean total enstropy with the mesh resolutions (right)
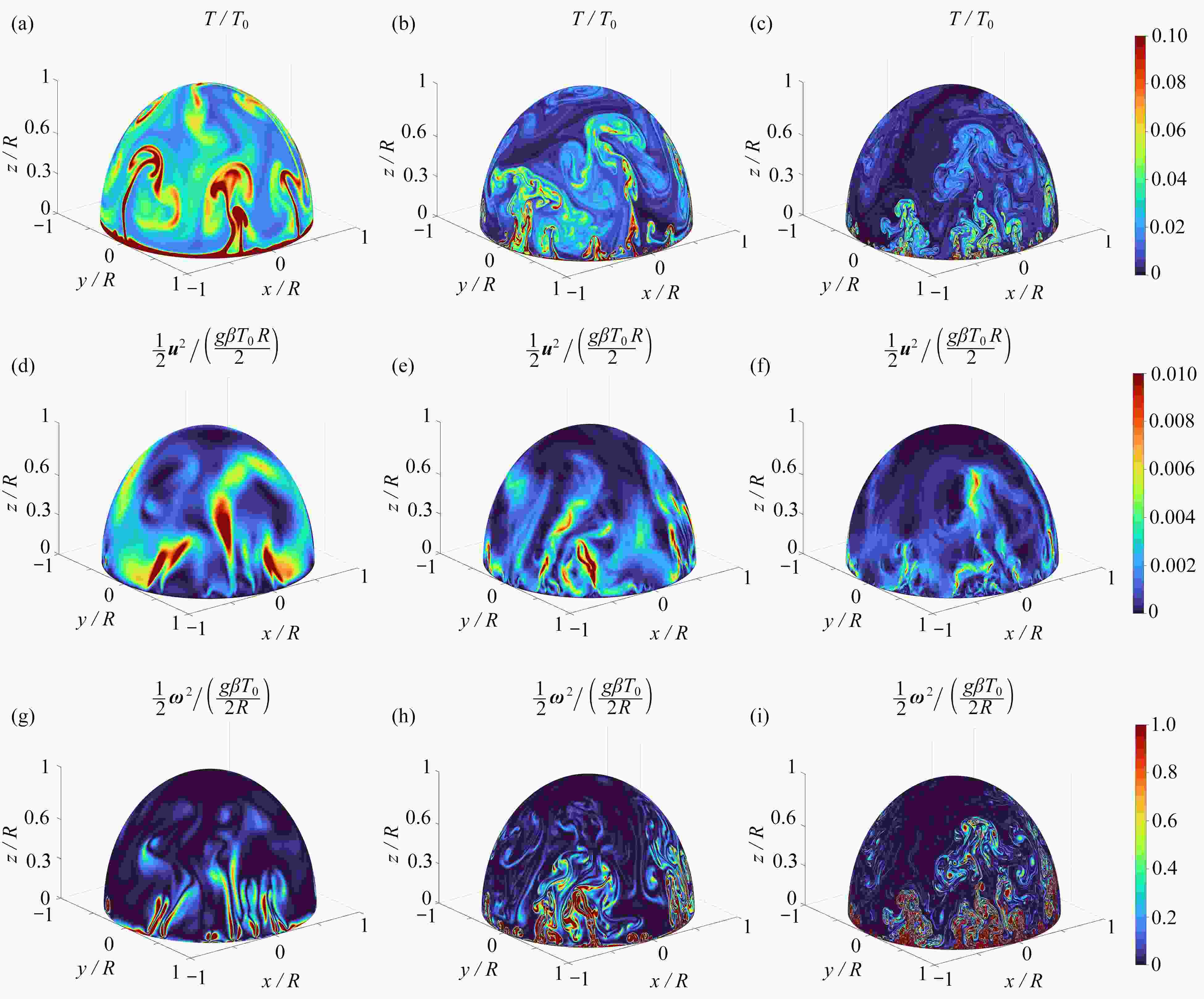
图 5 瞬时流场图：（a） 无量纲瞬时温度场，Ra=3×107；（b） 无量纲瞬时温度场，Ra=3×109；（c） 无量纲瞬时温度场，Ra=3×1011；（d） 无量纲瞬时动能场，Ra=3×107；（e） 无量纲瞬时动能场，Ra=3×109；（f） 无量纲瞬时动能场，Ra=3×1011；（g） 无量纲瞬时拟涡能场，Ra=3×107；（h） 无量纲瞬时拟涡能场，Ra=3×109；（i） 无量纲瞬时拟涡能场，Ra=3×1011
Figure 5. The instantaneous flow field: (a) dimensionless instantaneous temperature field, Ra=3×107; (b) dimensionless instantaneous temperature field, Ra=3×109; (c) dimensionless instantaneous temperature field, Ra=3×1011; (d) dimensionless instantaneous kinetic energy field, Ra=3×107; (e) dimensionless instantaneous kinetic energy field, Ra=3×109; (f) dimensionless instantaneous kinetic energy field, Ra=3×1011; (g) dimensionless instantaneous enstrophy field, Ra=3×107; (h) dimensionless instantaneous enstrophy field, Ra=3×109; (i) dimensionless instantaneous enstrophy field, Ra=3×1011
图 6 动能与拟热能的波数谱：（a） 动能；（b） 拟热能
Figure 6. The wave number spectra for the kinetic energy and entropy: (a) the kinetic energy; (b) the entropy
图 7 肥皂泡上的动能通量、拟涡能通量、拟热能通量和浮力的通量：（a） 动能；（b） 拟涡能；（c） 拟热能；（d） 浮力
Figure 7. The fluxes of kinetic energy, enstrophy, entropy and buoyancy on the soap bubble: (a) the kinetic energy; (b) the enstrophy; (c) the entropy; (d) the buoyancy
图 8 结构函数计算方法
Figure 8. The scheme of the distance for calculating the structure function
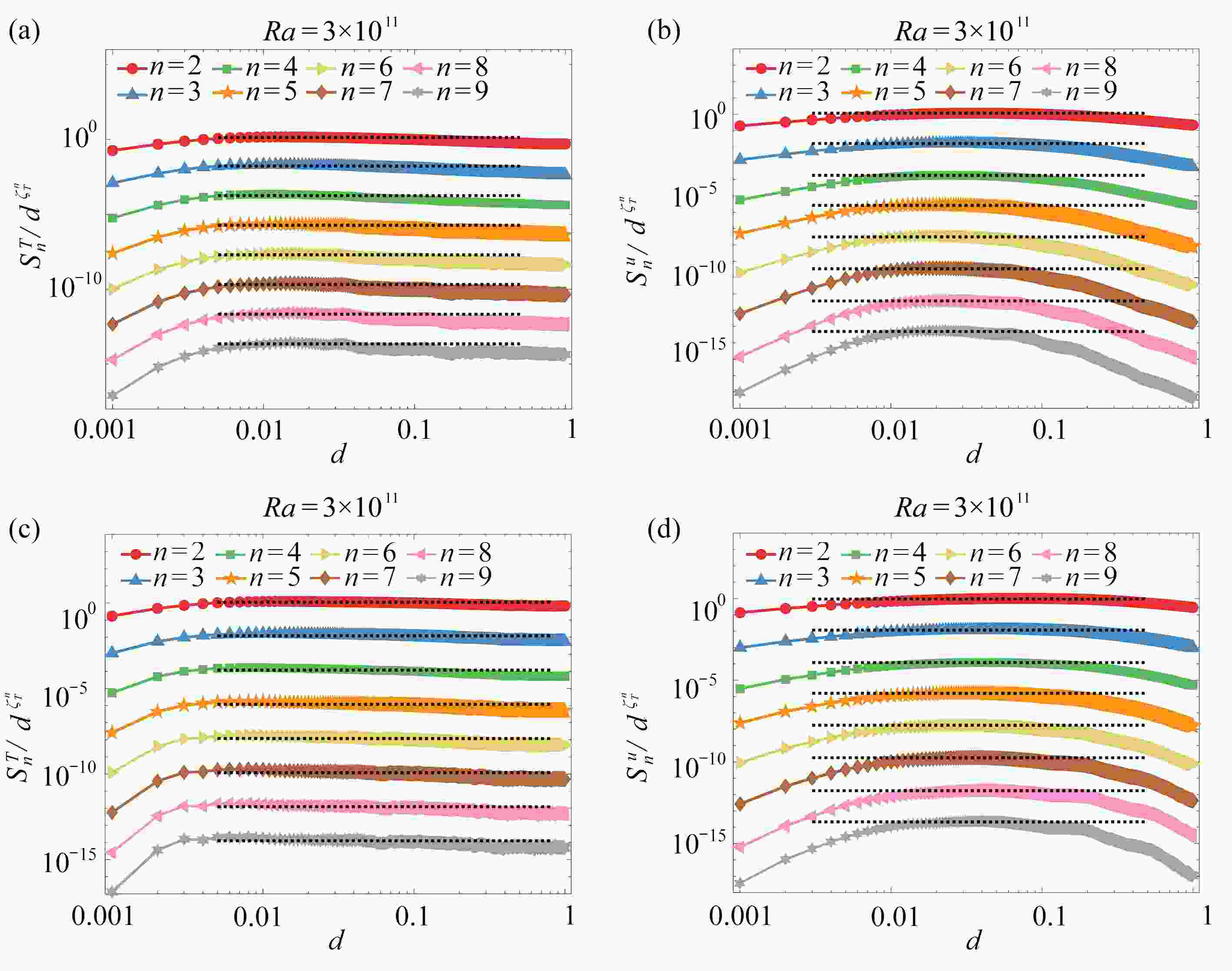
图 9 纬度与经度方向上2到9阶的温度和速度结构函数：（a） 纬度方向的温度结构函数；（b） 纬度方向的速度结构函数；（c） 经度方向的温度结构函数；（d） 经度方向的速度结构函数
Figure 9. The temperature and velocity structure functions in the latitude and longitude directions, n=2~9: (a) the temperature structure functions in the latitude direction; (b) the velocity structure functions in the latitude direction; (c) the temperature structure functions in the longitude direction; (d) the velocity structure functions in the longitude direction
算法1 共轭梯度算法 1 $ {\boldsymbol{r}} = \bar{\bar{{\boldsymbol{A}}}}{\boldsymbol{T}} - {\boldsymbol{C}} $; 2 $ {\boldsymbol{d}} = {\boldsymbol{r}} $; 3 while $ \| \bar{\bar{{\boldsymbol{A}}}}{\boldsymbol{T}} - {\boldsymbol{C}}\| \geqslant \xi $ do 4 ${\boldsymbol{a}} = \dfrac{{\boldsymbol{r}}^{{\rm{T}}}{\boldsymbol{r}}}{{\boldsymbol{d}}^{{\rm{T}}}\bar{\bar{{\boldsymbol{A}}}}{\boldsymbol{d}}}$; 5 $ {\boldsymbol{T}} = {\boldsymbol{T}} + {\boldsymbol{a}}{\boldsymbol{d}} $; 6 $\,\dot{\beta} = \dfrac{\left|\bar{\bar{{\boldsymbol{A}}}}{\boldsymbol{T}} - {\boldsymbol{C}}\right|^2}{|{\boldsymbol{r}}|^2}$; 7 $ {\boldsymbol{r}} = \bar{\bar{{\boldsymbol{A}}}}{\boldsymbol{T}} - {\boldsymbol{C}} $; 8 $ {\boldsymbol{d}} = {\boldsymbol{r}} + \dot{\beta}{\boldsymbol{d}} $。 
下载: 导出CSV
算法2 V循环算法 1 while $ \| {\boldsymbol{U}}_p - \bar{\bar{{\boldsymbol{L}}}}_{p} {\boldsymbol{B}}_p\| \geqslant \xi $ do 2 $ {\boldsymbol{U}}_{p} = \widetilde{S}_{n}(\bar{\bar{{\boldsymbol{L}}}}_p, {\boldsymbol{U}}_{p}^{0}, {\boldsymbol{B}}_p) $; /* Correction on coarse grids */ 3 for $ n = q-1, q-2, q-3, \cdots, 2 $ do 4 $ \dot{{\boldsymbol{U}}}_{n}=R^{n+1}_{n}{\boldsymbol{U}}_{n+1} $; 5 $ {\boldsymbol{B}}_i = R^{n+1}_{n}({\boldsymbol{B}}_{n+1}-\bar{\bar{{\boldsymbol{L}}}}_{n+1}{\boldsymbol{U}}_{n+1}) + \bar{\bar{{\boldsymbol{L}}}}_{n} \dot{{\boldsymbol{U}}}_{n} $; 6 $ {\boldsymbol{U}}_{n}=\widetilde{S}_{n}(\bar{\bar{{\boldsymbol{L}}}}_{n}, \dot{{\boldsymbol{U}}}_{n}, {\boldsymbol{B}}_{n}) $; /* Updating the fine grids */ 7 for $ n = 2, 3, 4, \cdots, q $ do 8 $ \ddot{{\boldsymbol{U}}}_{n}={\boldsymbol{U}}_{n} + P^{n}_{n+1}({\boldsymbol{U}}_{n-1} - \dot{{\boldsymbol{U}}}_{n-1}) $; 9 $ {\boldsymbol{U}}_{n}=\widetilde{S}_{n}(\bar{\bar{{\boldsymbol{L}}}}_{n}, \ddot{{\boldsymbol{U}}}_{n}, {\boldsymbol{B}}_{n}) $; 10 $ {\boldsymbol{U}}^{0}_{p} = {\boldsymbol{U}}_{p} $。 // Update initial solution
下载: 导出CSV
表 1 算例参数信息
Table 1. Information for the simulated cases
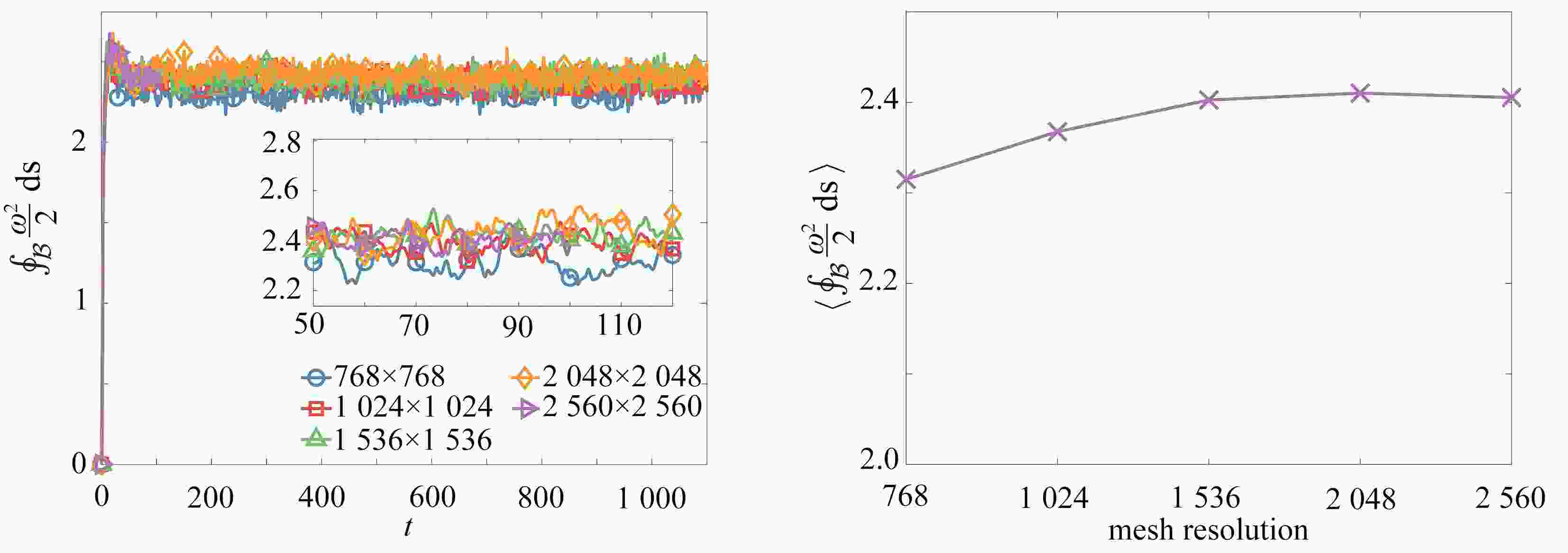
case number $ Ra $ $ Pr $ $\hat{ S}$ $\hat{F}$ resolution 1 $ 3\times10^{7} $ $ 7 $ $0.06$ $0.06$ $ 1\;024\times1\;024 $ 2 $ 3\times10^{9} $ $ 7 $ $0.06$ $0.06$ $ 2\;048\times2\;048 $ 3 $ 3\times10^{11} $ $ 7 $ $0.06$ $0.06$ $ 2\;048\times2\;048 $
下载: 导出CSV
-
[1] LOHSE D, XIA K Q. Small-scale properties of turbulent Rayleigh-Bénard convection[J]. Annual Review of Fluid Mechanics, 2010, 42: 335-364. doi: 10.1146/annurev.fluid.010908.165152 [2] 彭世彬, 郭瑞, 冯上升, 等. 主动冷却点阵夹层防热结构温度响应计算模型[J]. 应用数学和力学, 2022, 43(5): 477-489PENG Shibin, GUO Rui, FENG Shangsheng, et al. A calculation model for temperature responses of active cooling lattice sandwich structures for thermal protection[J]. Applied Mathematics and Mechanics, 2022, 43(5): 477-489.(in Chinese) [3] BOFFETTA G, ECKE R E. Two-dimensional turbulence[J]. Annual Review of Fluid Mechanics, 2012, 44: 427-451. doi: 10.1146/annurev-fluid-120710-101240 [4] 宁利中, 张迪, 宁碧波, 等. 侧向局部加热对流的周期性[J]. 应用数学和力学, 2020, 41(2): 125-133NING Lizhong, ZHANG Di, NING Bibo, et al. Periodicity of convection under lateral local heating[J]. Applied Mathematics and Mechanics, 2020, 41(2): 125-133.(in Chinese) [5] 宁利中, 张珂, 宁碧波, 等. 侧向加热腔体中的多圈型对流斑图[J]. 应用数学和力学, 2020, 41(3): 250-259NING Lizhong, ZHANG Ke, NING Bibo, et al. Multi-roll type convection patterns in cavities heated laterally[J]. Applied Mathematics and Mechanics, 2020, 41(3): 250-259.(in Chinese) [6] 宁利中, 宁碧波, 胡彪, 等. 具有水平流动的对流斑图成长和动力学特性[J]. 应用数学和力学, 2020, 41(10): 1146-1156NING Lizhong, NING Bibo, HU Biao, et al. Growth and dynamics of convection patterns with horizontal flow[J]. Applied Mathematics and Mechanics, 2020, 41(10): 1146-1156.(in Chinese) [7] KRAICHNAN R H. Inertial ranges in two-dimensional turbulence[J]. Physics of Fluids, 1967, 10(7): 1417-1423. doi: 10.1063/1.1762301 [8] LEITH C E. Diffusion approximation for two-dimensional turbulence[J]. The Physics of Fluids, 1968, 11(3). DOI: 10.1063/1.1691968. [9] BATCHELOR G K. Computation of the energy spectrum in homogeneous two-dimensional turbulence[J]. Physics of Fluids, 1969, 12(11): 233. [10] 施惟慧, 沈春, 王曰朋. 大气运动基本方程组的解析解[J]. 应用数学和力学, 2007, 28(3): 349-358 doi: 10.3321/j.issn:1000-0887.2007.03.011SHI Weihui, SHEN Chun, WANG Yuepeng. Analytical solution of the basic equations set of atmospheric motion[J]. Applied Mathematics and Mechanics, 2007, 28(3): 349-358.(in Chinese) doi: 10.3321/j.issn:1000-0887.2007.03.011 [11] 郭连红, 李远飞. 大尺度湿大气原始方程组对边界参数的连续依赖性[J]. 应用数学和力学, 2020, 41(9): 1036-1047GUO Lianhong, LI Yuanfei. Continuous dependence on boundary parameters of the original equations for large scale wet atmosphere[J]. Applied Mathematics and Mechanics, 2020, 41(9): 1036-1047.(in Chinese) [12] KELLAY H, GOLDBURG W I. Two-dimensional turbulence: a review of some recent experiments[J]. Reports on Progress in Physics, 2002, 65(5): 845-894. doi: 10.1088/0034-4885/65/5/204 [13] KELLAY H. Hydrodynamics experiments with soap films and soap bubbles: a short review of recent experiments[J]. Physics of Fluids, 2017, 29(11): 111113. doi: 10.1063/1.4986003 [14] SEYCHELLES F, AMAROUCHENE Y, BESSAFI M, et al. Thermal convection and emergence of isolated vortices in soap bubbles[J]. Physics Review Letter, 2008, 100(14): 144501. doi: 10.1103/PhysRevLett.100.144501 [15] MEUEL T, XIONG Y L, FISCHER P, et al. Intensity of vortices: from soap bubbles to hurricanes[J]. Scientific Report, 2013, 3: 3455. doi: 10.1038/srep03455 [16] SEYCHELLES F, INGREMEAU F, PRADERE C, et al. From intermittent to nonintermittent behavior in two dimensional thermal convection in a soap bubble[J]. Physics Review Letter, 2010, 105(26): 264502. doi: 10.1103/PhysRevLett.105.264502 [17] MEUEL T, PRADO G, SEYCHELLES F, et al. Hurricane track forecast cones from fluctuations[J]. Scientific Report, 2012, 2: 446. doi: 10.1038/srep00446 [18] MEUEL T, COUDERT M, FISCHER P, et al. Effects of rotation on temperature fluctuations in turbulent thermal convection on a hemisphere[J]. Scientific Report, 2018, 8: 16513. doi: 10.1038/s41598-018-34782-0 [19] BRUNEAU C H, FISCHER P, XIONG Y L, et al. Numerical simulations of thermal convection on a hemisphere[J]. Physical Review Fluids, 2018, 3: 043502. doi: 10.1103/PhysRevFluids.3.043502 [20] XIONG Y L, FISCHER P, BRUNEAU C H. Numerical simulations of two-dimensional turbulent thermal convection on the surface of a soap bubble[C]//Proceedings of the 7th International Conference on Computational Fluid Dynamics. 2012: ICCFD7-3703. [21] HE X Q, BRAGG A D, XIONG Y L, et al. Turbulence and heat transfer on a rotating, heated half soap bubble[J]. Journal of Fluid Mechanics, 2021, 924: A19. doi: 10.1017/jfm.2021.610 [22] STEVENS J A M R, CLERCX J H H, LOHSE D. Heat transport and flow structure in rotating Rayleigh-Bénard convection[J]. Journal of Computational Physics, 2013, 40: 41-49. [23] 许丁, 陈刚, 王娴, 等. 基于多GPU的格子Boltzmann法对槽道湍流的直接数值模拟[J]. 应用数学和力学, 2013, 34(9): 956-964 doi: 10.3879/j.issn.1000-0887.2013.09.009XU Ding, CHEN Gang, WANG Xian, et al. Direct numerical simulation of the wall-bounded turbulent flow by lattice Boltzmann method based on multi-GPU[J]. Applied Mathematics and Mechanics, 2013, 34(9): 956-964.(in Chinese) doi: 10.3879/j.issn.1000-0887.2013.09.009 [24] 沈露予, 陆昌根, 朱晓清. 自由来流湍流与三维壁面局部粗糙诱导平板边界层不稳定T-S波的数值研究[J]. 应用数学和力学, 2017, 38(11): 1208-1221SHEN Luyu, LU Changgen, ZHU Xiaoqing. Numerical study of unstable T-S waves excited by interaction between free-stream turbulence and 3D localized wall roughness in flat-plate boundary layer[J]. Applied Mathematics and Mechanics, 2017, 38(11): 1208-1221.(in Chinese) [25] 魏剑英, 葛永斌. 一种求解三维非稳态对流扩散反应方程的高精度有限差分格式[J]. 应用数学和力学, 2022, 43(2): 187-197WEI Jianying, GE Yongbin. A high-order finite difference scheme for 3D unsteady convection diffusion reaction equations[J]. Applied Mathematics and Mechanics, 2022, 43(2): 187-197.(in Chinese) [26] BOFFETTA G, MAZZINO A. Incompressible Rayleigh-Taylor turbulence[J]. Annual Review of Fluid Mechanics, 2017, 49: 119-143. doi: 10.1146/annurev-fluid-010816-060111 -
计量
- 文章访问数: 654
- HTML全文浏览量: 499
- PDF下载量: 77
- 被引次数: 0
渝公网安备50010802005915号