Dynamic Responses Analysis of Bridges With Uncertain Parameters Under Moving Loads
-
摘要:
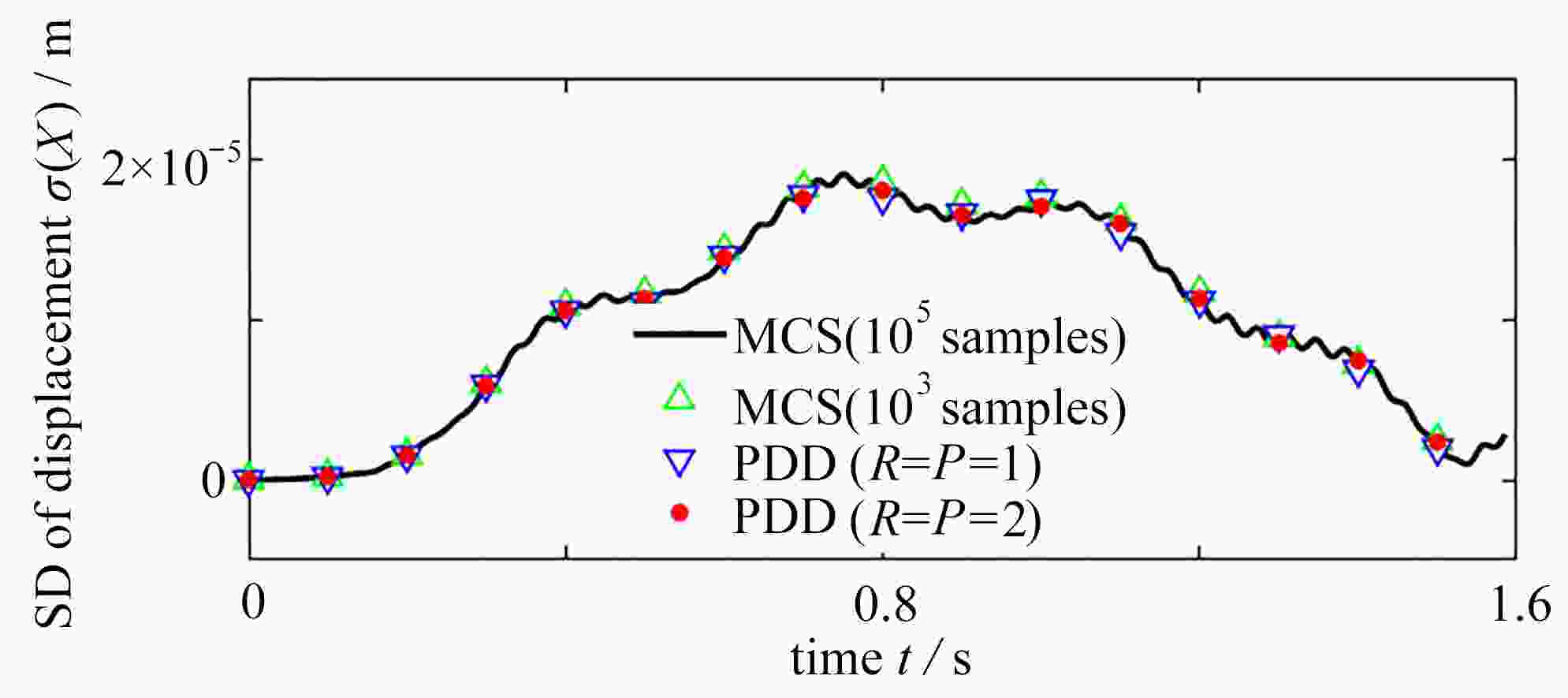
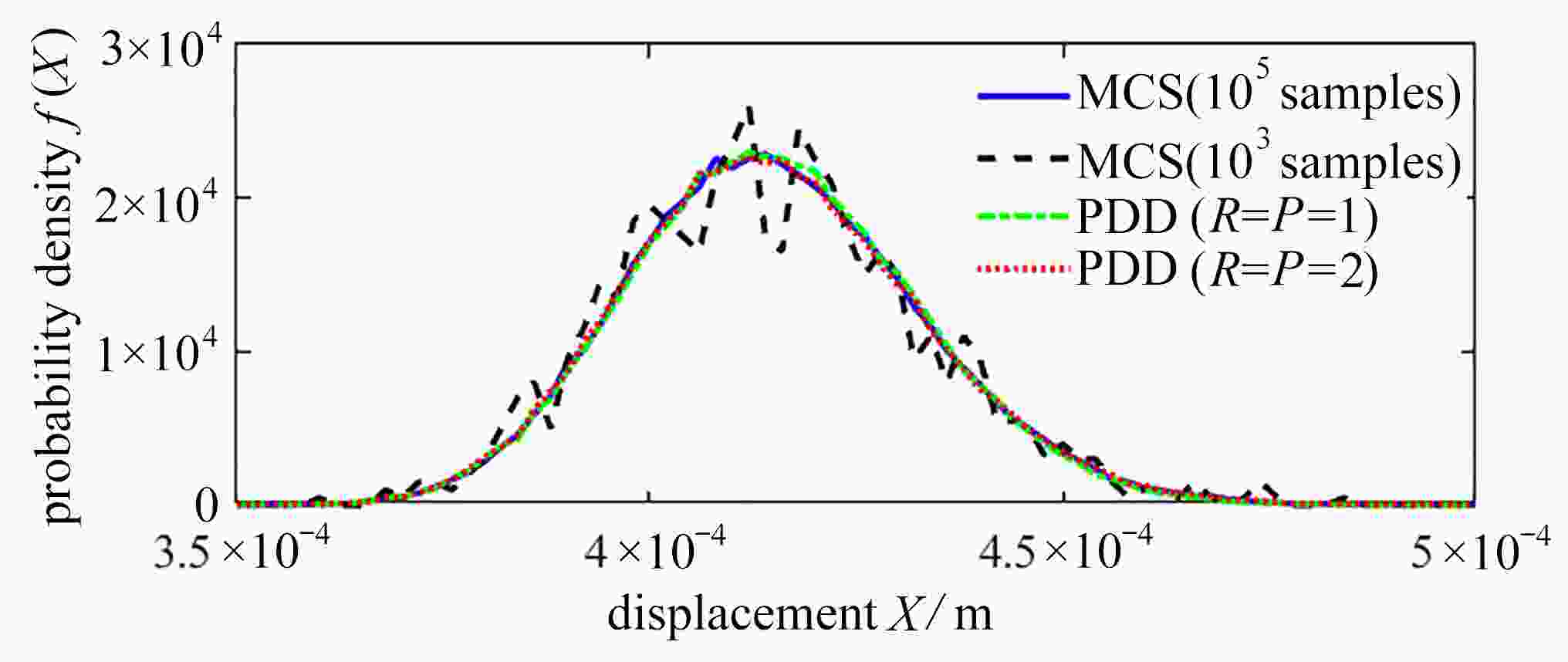
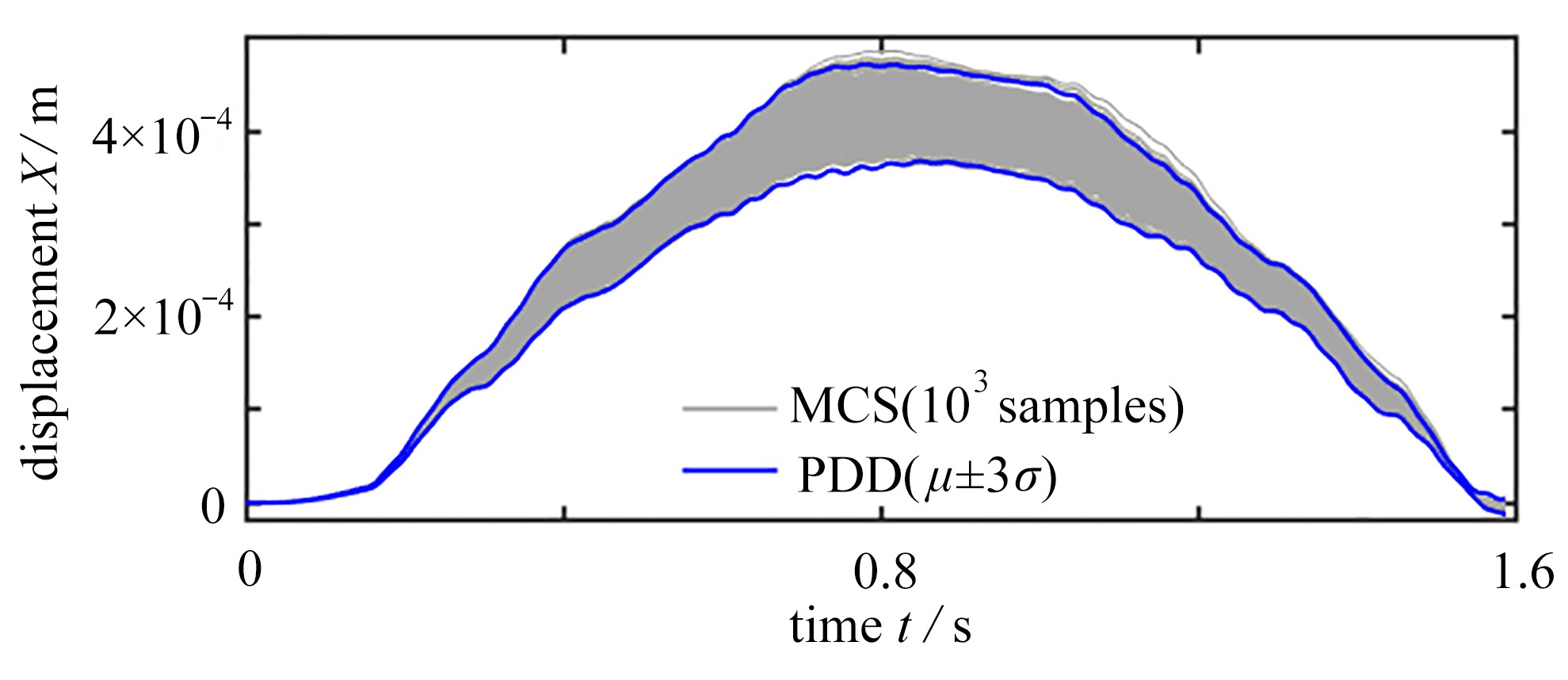
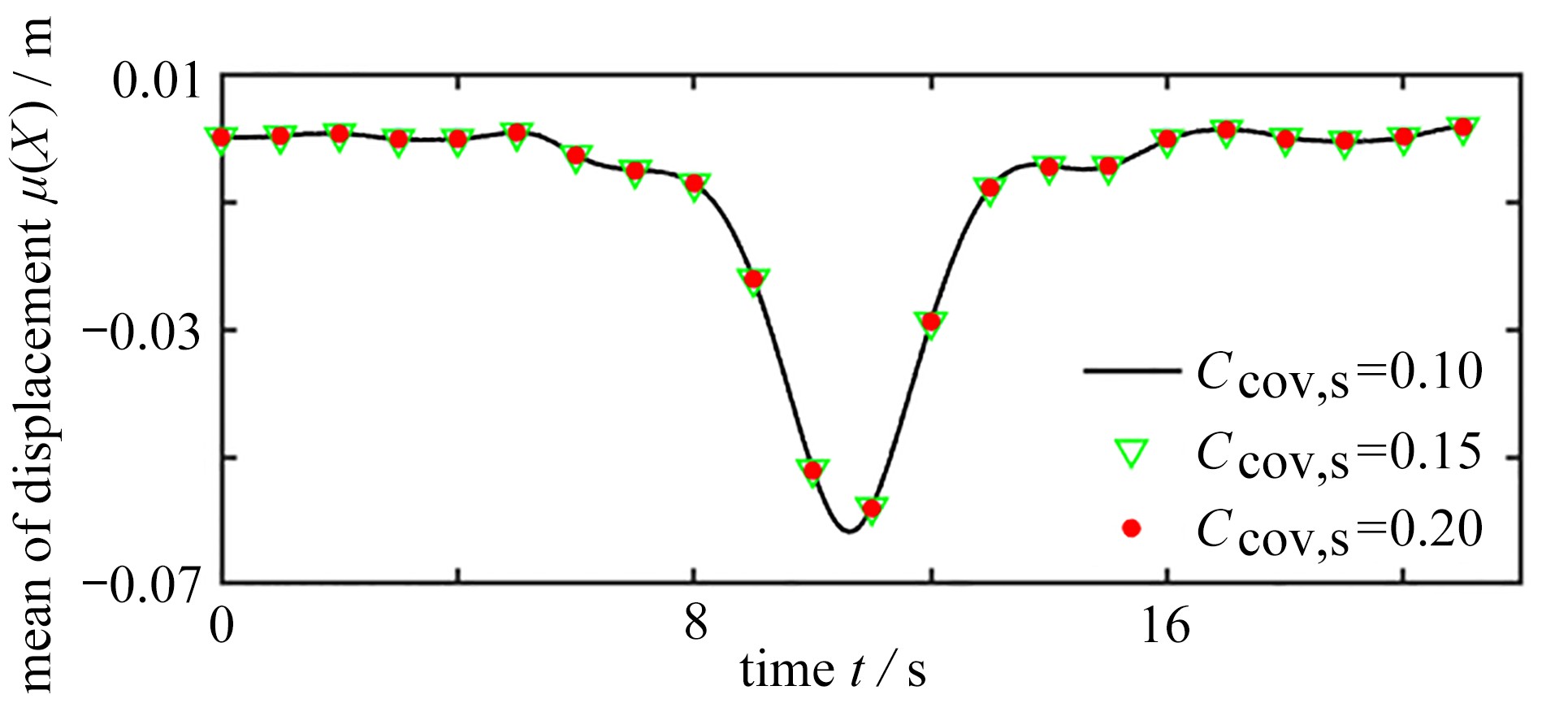
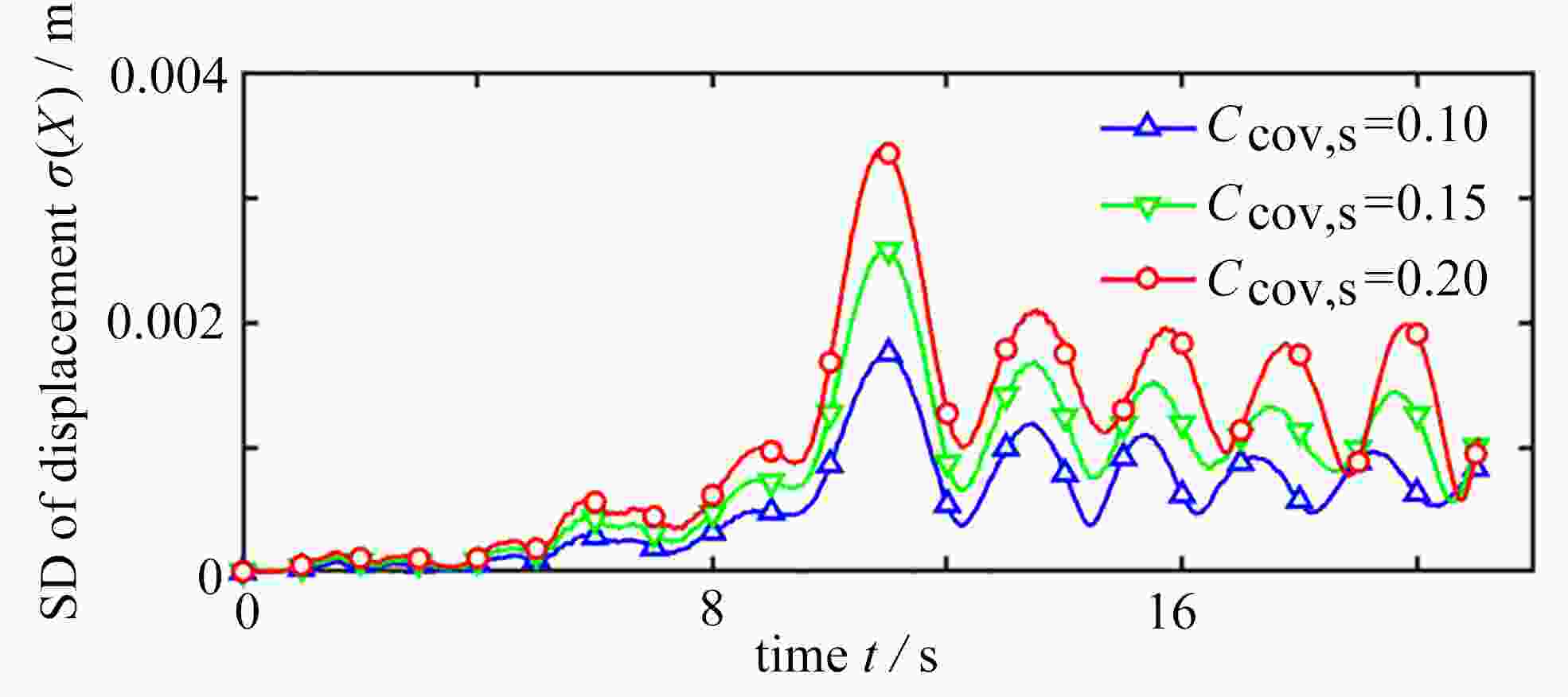
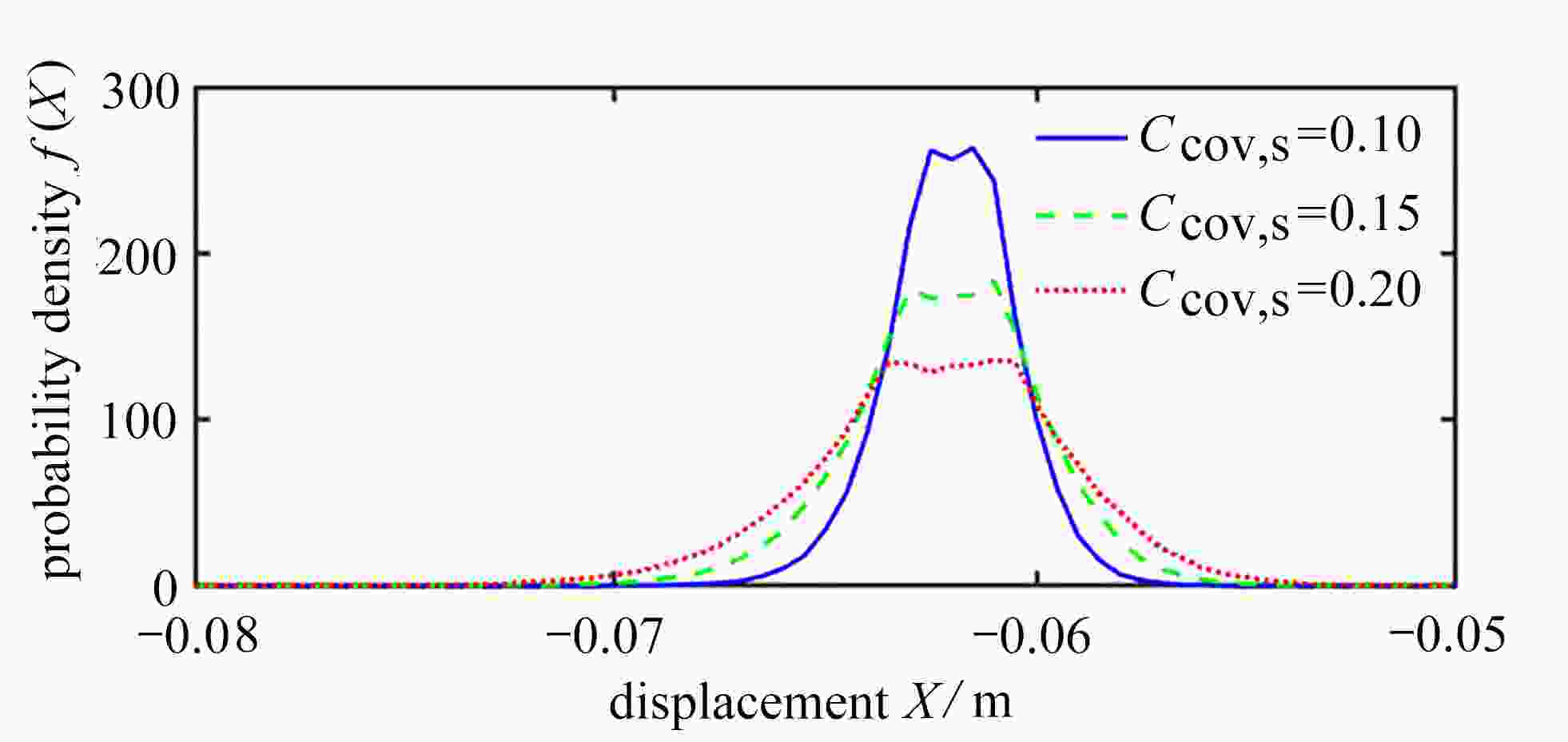
针对具有不确定参数桥梁在移动荷载作用下的动力响应分析，首次建立了移动荷载作用下桥梁响应分析的多项式维数分解法。将结构的不确定参数视为独立的随机变量，构造了结构动力响应关于不确定参数的随机函数；进而采用一组变量数目逐次增加的成员函数实现结构动力响应的维数分解，并利用Fourier多项式展开推导成员函数的近似显式表达。通过降维积分方法降低概率空间内的积分维度，高效地实现了展开系数的计算。在数值算例中，进行了具有不确定参数桥梁在移动荷载作用下的响应估计，并与Monte-Carlo模拟进行对比，验证了该文方法的精确性和效率。
Abstract:The dynamic responses of bridges with uncertain parameters under moving loads were analyzed, and a polynomial dimensional decomposition method for the analysis of structural responses induced by moving loads was proposed for the first time. The uncertain parameters were regarded as independent random variables, and the random response function about these uncertain parameters was constructed. The dimensional decomposition of the function was further performed with a group of component functions with a gradually increasing number of variables, and the approximate expressions of the component functions were derived through the Fourier polynomial expansion. Then, the expansion coefficients were efficiently calculated through the introduction of the dimension-reduction integration method. The numerical examples give response estimation of bridges with uncertain parameters under moving loads, which in comparison with those from the Monte-Carlo simulation, verify the accuracy and efficiency of the proposed method.
-
图 4
$ t=0.8\;\mathrm{s} $ 时跨中位移的概率密度Figure 4. The probability density of displacement at
$ t=0.8\;\mathrm{s} $ 
图 9
$ t=10.60\;\mathrm{s} $ 时的概率密度Figure 9. The probability density at
$ t=10.60\;\mathrm{s} $ -
[1] 高庆飞, 张坤, 刘晨光, 等. 移动车辆荷载作用下桥梁冲击系数的若干讨论[J]. 哈尔滨工业大学学报, 2020, 52(3): 44-50 doi: 10.11918/201903144GAO Qingfei, ZHANG Kun, LIU Chenguang, et al. Discussions on the impact of bridges subjected to moving vehicular loads[J]. Journal of Harbin Institute of Technology, 2020, 52(3): 44-50.(in Chinese) doi: 10.11918/201903144 [2] LAI Z P, JING L Z, ZHOU W B. An analytical study on dynamic response of multiple simply supported beam system subjected to moving loads[J]. Shock and Vibration, 2018, 2018: 2149251. [3] LIU S H, JIANG L Z, ZHOU W B, et al. Dynamic response analysis of multi-span bridge-track structure system under moving loads[J]. Mechanics Based Design of Structures and Machines, 2021. DOI: 10.1080/ 15397734.2021.2010569. [4] 阳霞, 张静, 任伟新, 等. 车辆荷载作用下桥梁应变极值估计的阈值选取[J]. 应用数学和力学, 2017, 38(5): 503-512YANG Xia, ZHANG Jing, REN Weixin, et al. Threshold selection for the extreme value estimation of bridge strain under vehicle load[J]. Applied Mathematics and Mechanics, 2017, 38(5): 503-512.(in Chinese) [5] CHANG T P. Stochastic dynamic finite element analysis of bridge-vehicle system subjected to random material properties and loadings[J]. Applied Mathematics & Computation, 2014, 242: 20-35. [6] NI P, XIA Y, LI J, et al. Using polynomial chaos expansion for uncertainty and sensitivity analysis of bridge structures[J]. Mechanical Systems and Signal Processing, 2019, 119: 293-311. doi: 10.1016/j.ymssp.2018.09.029 [7] WU S Q, LAW S S. Evaluating the response statistics of an uncertain bridge-vehicle system[J]. Mechanical Systems and Signal Processing, 2012, 27: 576-589. doi: 10.1016/j.ymssp.2011.07.019 [8] WU S Q, LAW S S. A reduced polynomial chaos expansion model for stochastic analysis of a moving load on beam system with non-Gaussian parameters[J]. Journal of Vibroengineering, 2015, 17(3): 1560-1577. [9] 万华平, 邰永敢, 钟剑, 等. 基于多项式混沌展开的结构动力特性高阶统计矩计算[J]. 应用数学和力学, 2018, 39(12): 1331-1342WAN Huaping, TAI Yonggan, ZHONG Jian, et al. Computation of high-order moments of structural dynamic characteristics based on polynomial chaos expansion[J]. Applied Mathematics and Mechanics, 2018, 39(12): 1331-1342.(in Chinese) [10] RAHMAN S. A polynomial dimensional decomposition for stochastic computing[J]. International Journal for Numerical Methods in Engineering, 2008, 76(13): 2091-2116. doi: 10.1002/nme.2394 [11] RAHMAN S. Probability distributions of natural frequencies of uncertain dynamic systems[J]. AIAA Journal, 2009, 47(6): 1579-1589. doi: 10.2514/1.42720 [12] LU K. Statistical moment analysis of multi-degree of freedom dynamic system based on polynomial dimensional decomposition method[J]. Nonlinear Dynamics, 2018, 93: 2003-2018. doi: 10.1007/s11071-018-4303-1 [13] LIU F, ZHAO Y. A hybrid method for analysing stationary random vibration of structures with uncertain parameters[J]. Mechanical Systems and Signal Processing, 2022, 164: 108259. doi: 10.1016/j.ymssp.2021.108259 [14] RAHMAN S. Global sensitivity analysis by polynomial dimensional decomposition[J]. Reliability Engineering and System Safety, 2011, 96(7): 825-837. doi: 10.1016/j.ress.2011.03.002 [15] XU H, RAHMAN S. A generalized dimension-reduction method for multidimensional integration in stochastic mechanics[J]. International Journal of Numerical Method in Engineering, 2004, 61(12): 1992-2019. doi: 10.1002/nme.1135 -
下载:
计量
- 文章访问数: 532
- HTML全文浏览量: 228
- PDF下载量: 81
- 被引次数: 0
渝公网安备50010802005915号