Simulation of Aerodynamic Performances of Flexible Flapping Wing Airfoils
-
摘要:
与固定翼相比,在低速、小Reynolds数条件下,扑翼飞行具有显著的气动性能优势,受到越来越多的重视。然而,目前对扑翼翼型的研究以刚性翼型为主,对柔性翼型气动性能认识还不清楚。该文建立了柔性椭圆翼型的流固耦合仿真模型,分析了不同风速、迎角下柔性椭圆翼型的周围流场、变形以及气动性能。仿真结果表明,较刚性翼型,柔性翼型延缓了尾涡脱落时间,有效降低升力扰动振荡频率;柔性翼型显著抑制了尾流流场的扰动,降低升力扰动振荡幅值,合适的弹性模量翼型使得扰动振荡完全消除。研究结果可为软飞行器气动设计提供参考。
Abstract:Compared with fixed wings, the flapping wing has a significant aerodynamic performance advantage at low speeds and low Reynolds numbers, which draws more and more attentions. But most previous studies focus on rigid flapping airfoils, the aerodynamic performances of flexible flapping airfoils are still unclear. A fluid-solid coupling model for the flexible elliptical airfoils was developed to analyze the flow field around the airfoil, the airfoil deformation and the aerodynamic characteristics of airfoils, at different wind speeds and attack angles. Compared with the rigid airfoil, the flexible airfoil can delay the shedding time of the wake vortex and reduce the oscillation frequency of the disturbance on the lift force. The flexible airfoil significantly suppresses the disturbance of the wake flow and reduces the oscillation amplitude of disturbance. Even, the airfoil disturbance oscillation can be completely eliminated at an appropriate Young’s modulus of the airfoil. These results provide a theoretical guidance for the design of soft aircraft.
-
Key words:
- flexible airfoil /
- fluid-solid coupling /
- aerodynamic performance /
- lift force /
- finite element
-
引 言
尽管微型飞行器技术有了很大的发展,但昆虫、鸟类等生物的飞行能力至今仍让人造飞行器望尘莫及,因此研究扑翼气动性能具有重要意义[1-3]。在以往的研究中,通常把扑翼翼型作为刚性翼型处理,忽略了其弹性变形的影响。刚性翼型在超过其相应的临界攻角时,会发生严重的流动分离,从而影响飞行器的飞行状态。而昆虫、鸟类等生物的翅膀在飞行中往往可以旋转较大角度且仍能保持平稳飞行。这不仅与其特殊的扑翼运动飞行方式有关,还与其柔性翼型结构有关。例如,Tang、Shyy等[4]采用梁模型研究了低Reynolds数下柔性平板翼型的气动性能,研究表明柔性结构在空气动力载荷作用下发生变形,表现出类似扑翼的俯仰运动,产生了明显的升力和推力。Visbal等[5]采用高保真隐式大涡模拟方法,研究了表面微柔性薄膜的SD7003翼型气动性能,研究表明柔性对膜翼型上流动结构使得升力增加和失速延迟。张兴伟、周超英等[6]通过弱流固耦合(仅考虑结构变形对流场的影响)方法分析了柔性扑翼变形的影响,发现适当的柔性变形可以提高升力、增大升阻比。王姝歆、周建华等[7]以昆虫的翅膀为基础,对柔性翅模型进行了合理的假设与简化,建立了柔性翅模型并进行了实验研究和分析,结果表明,柔性翅的柔性变形有助于改善飞行时的空气动力学特性。Kang等[8]研究了前缘处局部柔性翼的绕流问题,发现局部柔性翼型对提高升力有着积极的影响。进一步,陶真新等[9]数值分析了吸力面为三段柔性结构的NACA0012翼型的气动性能,发现翼面上表面的柔性起到提高升力、抑制流动分离的作用。
尽管以上研究已涉及柔性翼型气动性能的研究,但他们往往仅关注展向柔性变形或局部柔性变形的情况,多简化为薄膜、梁等简单结构进行建模,而缺乏对全局柔性翼型气动性能的研究。本研究以柔性椭圆扑翼翼型为例,建立有限元模型,分析不同来流风速、迎角下柔性椭圆翼型的空气动力学特性。
1. 刚性扑翼翼型空气动力学仿真分析
1.1 计算模型与网格划分
为了验证建模、仿真分析方法的有效性以及参数设置的合理性,首先对刚性椭圆翼型模型周围的流场进行仿真分析。利用ANSYS Workbench开展双向流固耦合计算,建立刚性翼型周围的流场模型,采用Meshing模块划分网格,调用计算流体力学Fluent模块,基于有限差分格式进行流场计算。
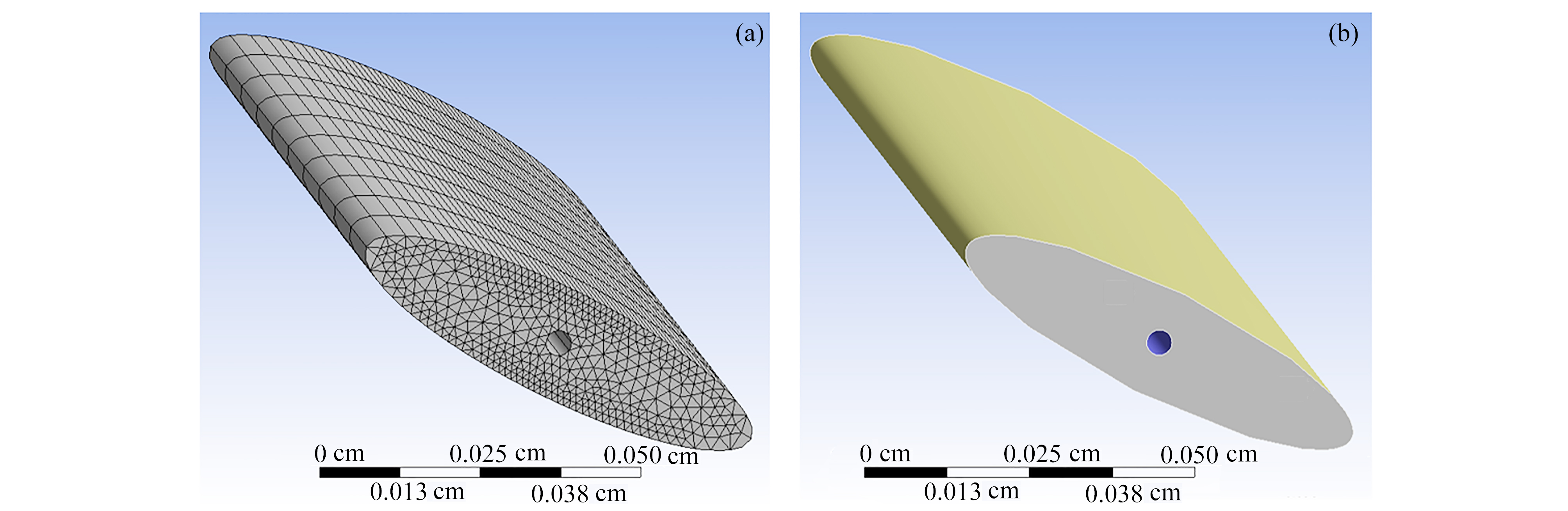
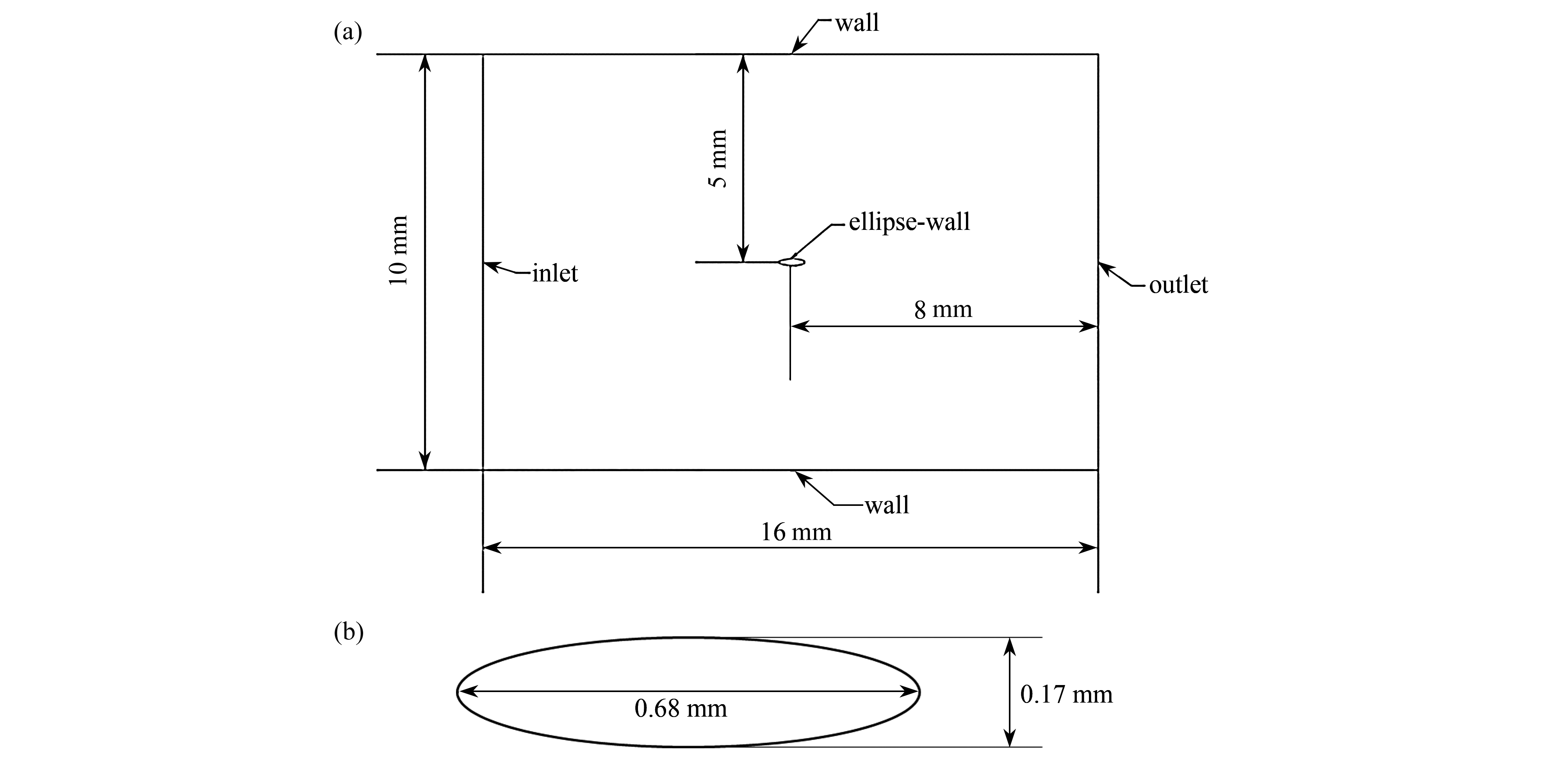
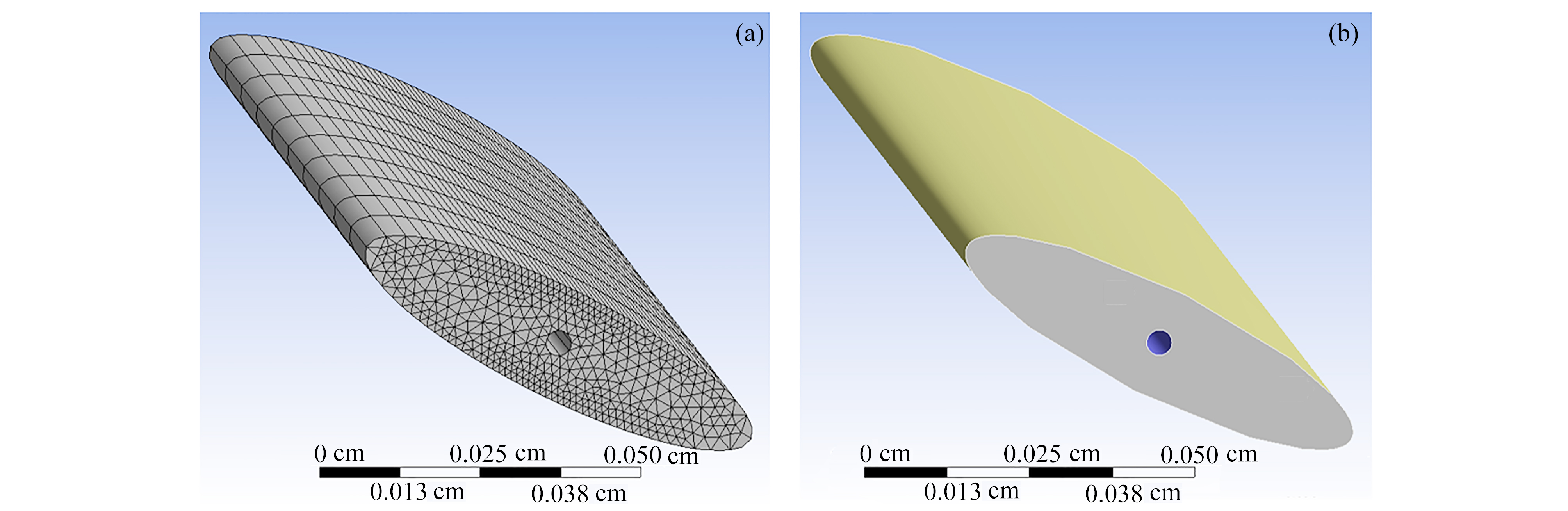
为了便于对比验证,扑翼翼型参考Pesavento和Wang所采用的果蝇翅膀尺寸[10],典型果蝇质量为1 mg,平均翼展长约为0.2 cm,椭圆翼型长轴长为0.068 cm,椭圆率为0.25(图1)。流场尺寸为16 mm × 10 mm,椭圆位于流场中央,翼型迎角为27.5°。流体介质为空气,速度为2.94 m/s,方向垂直于入口边界水平吹向椭圆翼型,左侧为流场的速度入口,右侧为出口,上下边界为固定壁面。
流场区域分为两部分,椭圆壁后尾流区与外围流场区,流场整体采用三角形非结构网格进行划分,如图2所示。为提高求解精度,同时也为了更好地呈现椭圆壁后流场,在尾迹区进行网格加密处理;同时为了提高计算效率,外围流场区采用较为稀疏的网格。考虑到低Reynolds数下椭圆壁边界层的黏性作用,椭圆边界层使用结构化网格进行加密处理,边界层网格膨胀率为1.1,共设置20层,网格厚度从壁面向外逐层递增,网格总数为19808。采用正交质量检查项进行网格质量检查,网格质量达到0.97。
在Fluent分析中,设置瞬态计算。由于果蝇的尺寸小,速度较低,在实际飞行中,其Reynolds数范围一般为102~104,因此在流场分析中主要分析其椭圆翼型低Reynolds数下的空气动力学特性,计算模型采用
k-ω SST湍流模型[11-12]。k-ω SST湍流模型湍动能k和其比耗散率ω的关系为ω=εβ∗k. (1) 变量k和ω的控制方程分别为
∂ρk∂t+∂ujk∂xj=τij∂ui∂xj−β∗ωk+∂∂xj[(μ+σkμt)∂k∂xj], (2a) ∂ρω∂t+∂ρujω∂xj=γνtτij∂ui∂xj−βρω2+∂∂xj[(μ+σωμt)∂k∂xj]+2(1−F1)ρσω2ω⋅∂k∂xj⋅∂ω∂xj. (2b) 方程(2a)和(2b)中右侧前三项分别为生成项、耗散项和扩散项,方程(2b)右侧最后一项为交叉扩散项,其中
τij=ut(2Sij−23∂uk∂xkδij)−23ρkδij, (3) Sij=12(∂ui∂xj+∂uj∂xi). (4) 式(1)~(4)中,
ε 为湍动能耗散率;ρ 为密度;ui,uj,uk 为速度分量;μ 为层流黏性;νt 为湍流运动黏性;β∗ ,β ,γ,σk ,σω 和σω2 为封闭常数。采用SIMPLE的二阶格式求解方法对N-S离散方程进行求解,提高求解精度。时间步长为0.000 1 s,共计算100个时间步,计算得到0.01 s内的结果。
1.2 模型验证
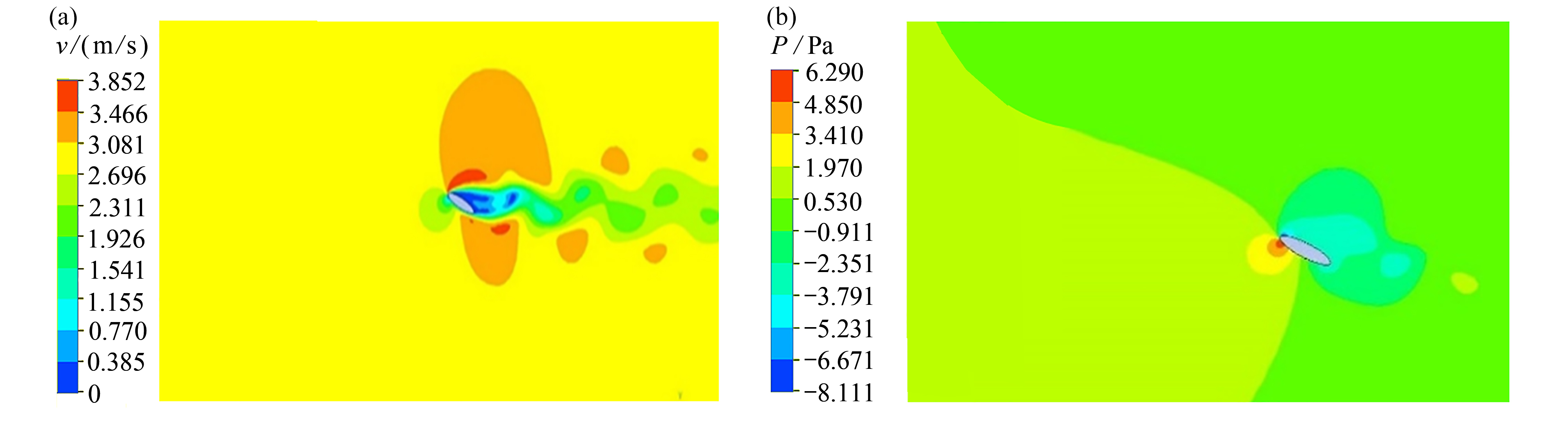
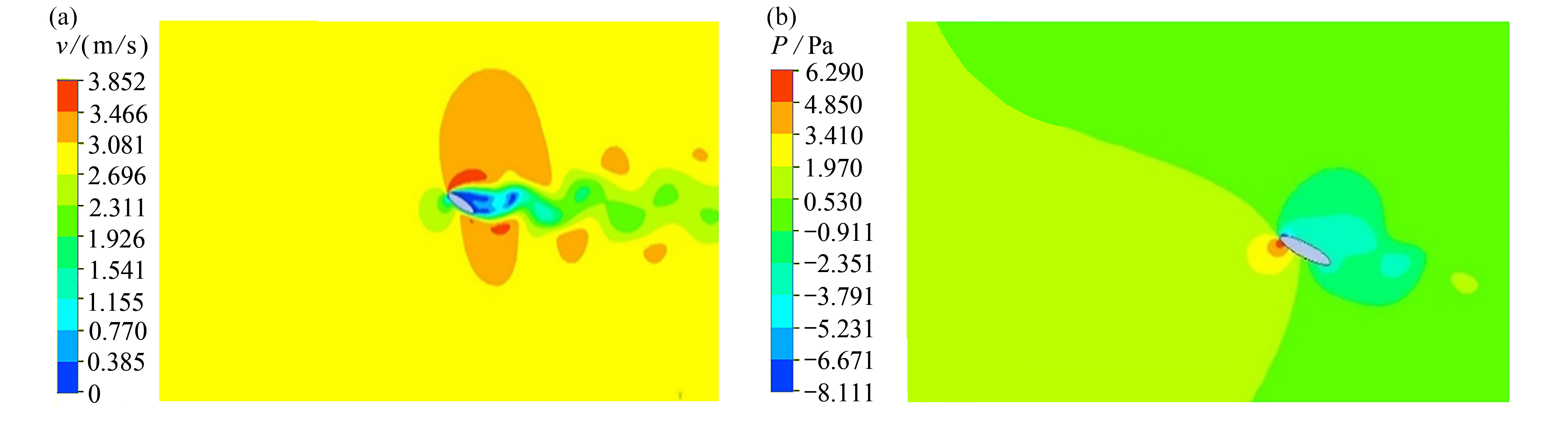
分别计算得到该模型流场的速度云图和压力云图(图3),椭圆翼型后产生了明显的周期性尾涡脱落,这一特征与Pesavento和Wang[10]数值计算的流场特征一致。
为了便于与文献结果定量对比验证,将时间无量纲化为
X=vtc, (5) 其中,
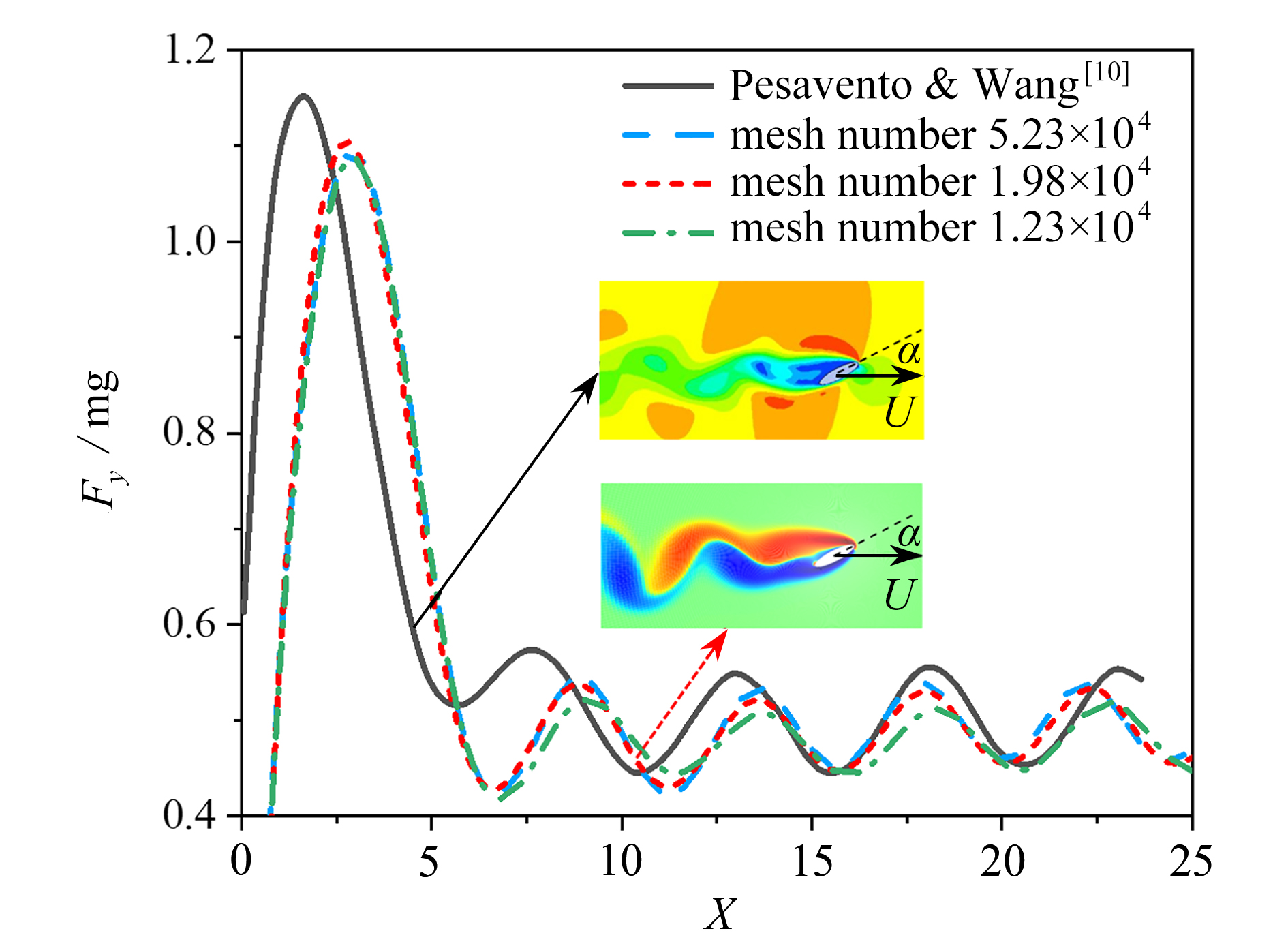
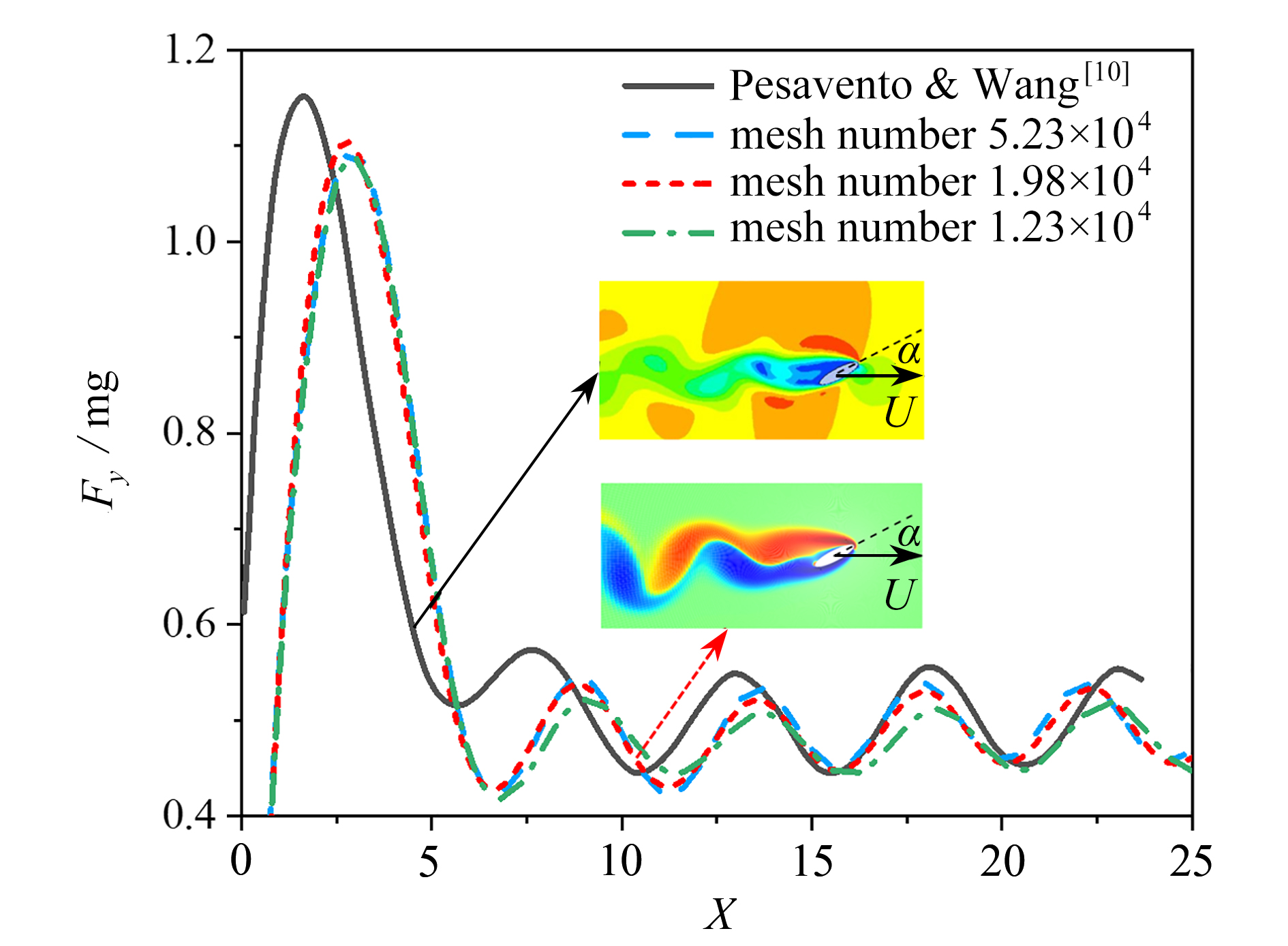
v 为来流速度,v =2.94 m/s;t 为时间;c 为椭圆翼型的弦长,c =0.68 mm。数值仿真计算所得椭圆翼型升力随时间的变化,开始阶段由于求解过程未收敛出现较大幅度扰动,随后升力值在0.4~0.6 mg之间呈现出周期性变化,周期约为4(图4)。这是因为翼型后缘出现周期性尾涡脱落。升力平均值约为0.5 mg,这是因为单只翅膀承担了果蝇重量。计算所得升力曲线的这些特征(扰动周期、平均升力),与Pesavento和Wang[10]的数值计算结果保持一致。表明所建立的模型、计算方法及参数设置等是有效的,可供后续研究。采用三种网格数量(1.23×104,1.98×104,5.23×104)进行了网格无关性验证,稀疏网格对升力峰值的监测不够,中等网格和密网格结果相近。因此,后续研究采用中等网格(即网格数1.98×104)即可满足计算精度。
1.3 不同风速、迎角下的流场及气动性能
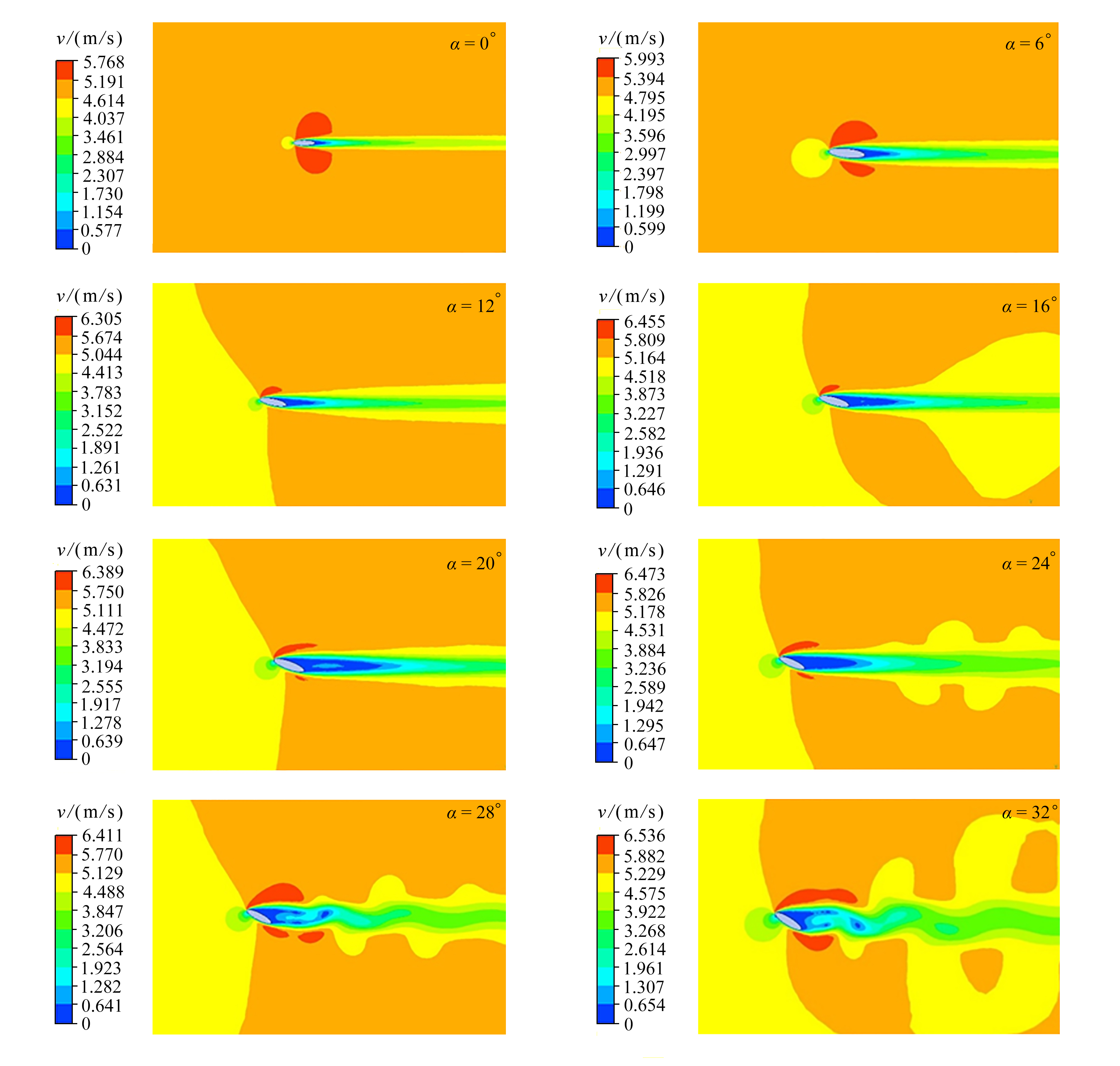
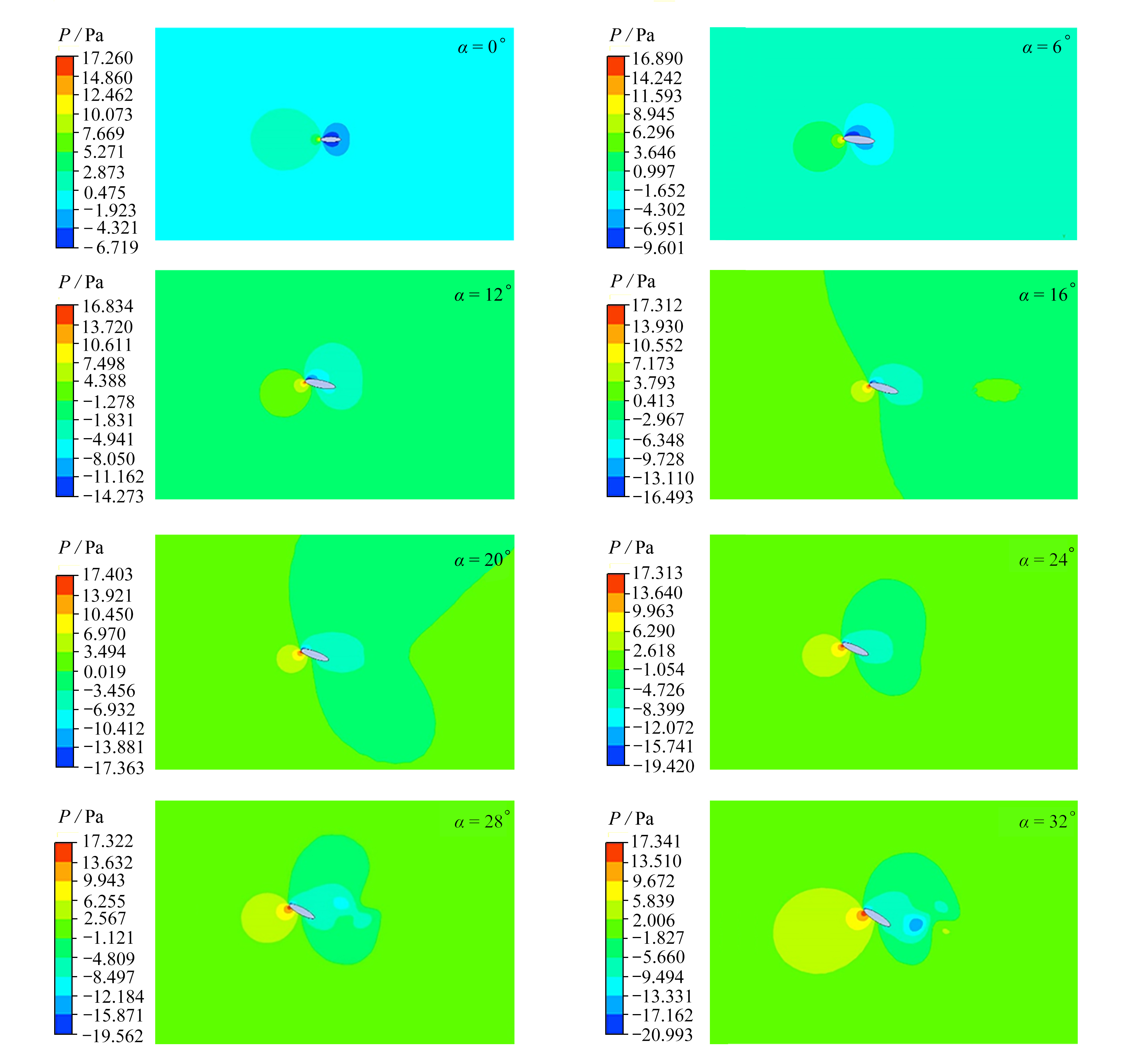
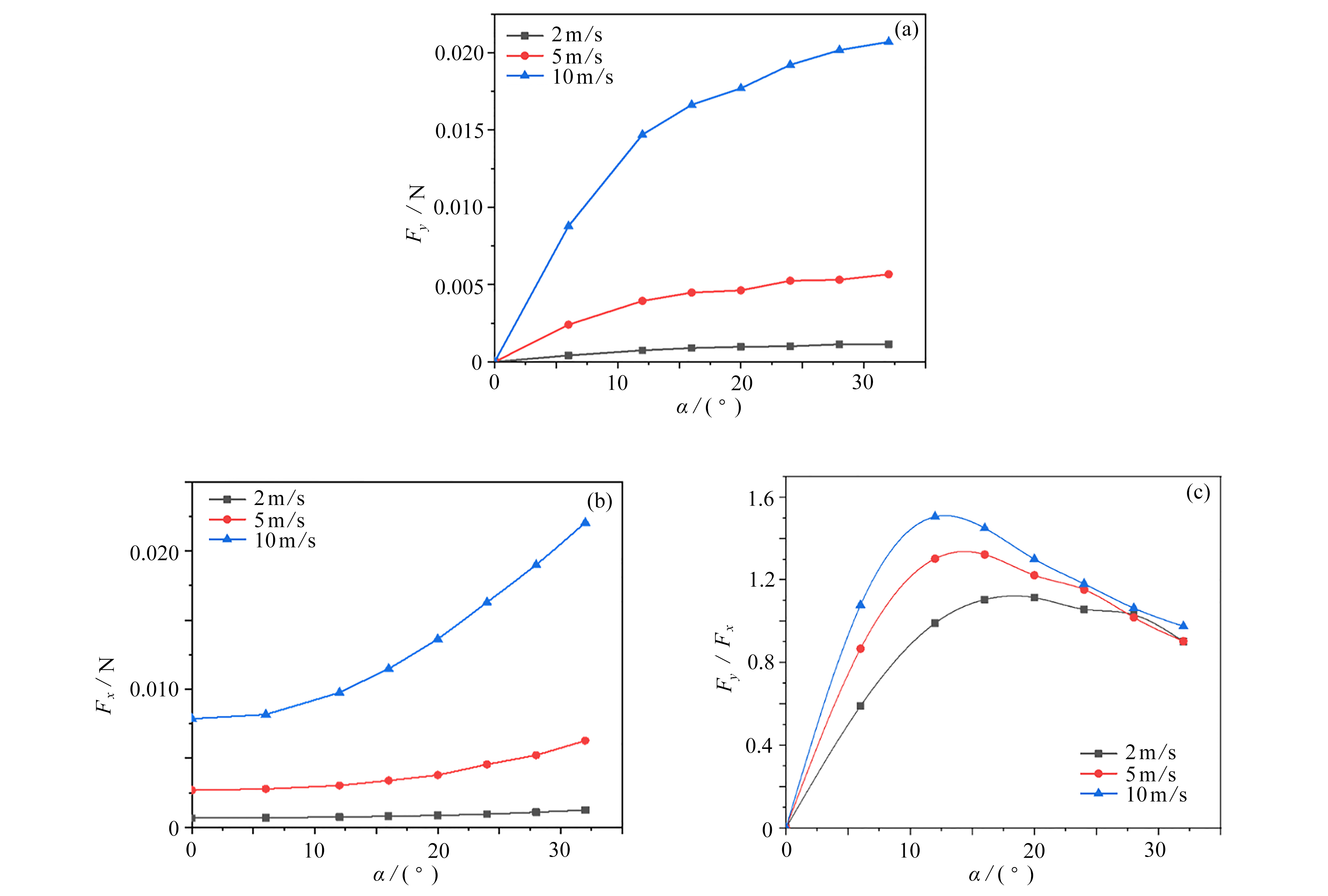
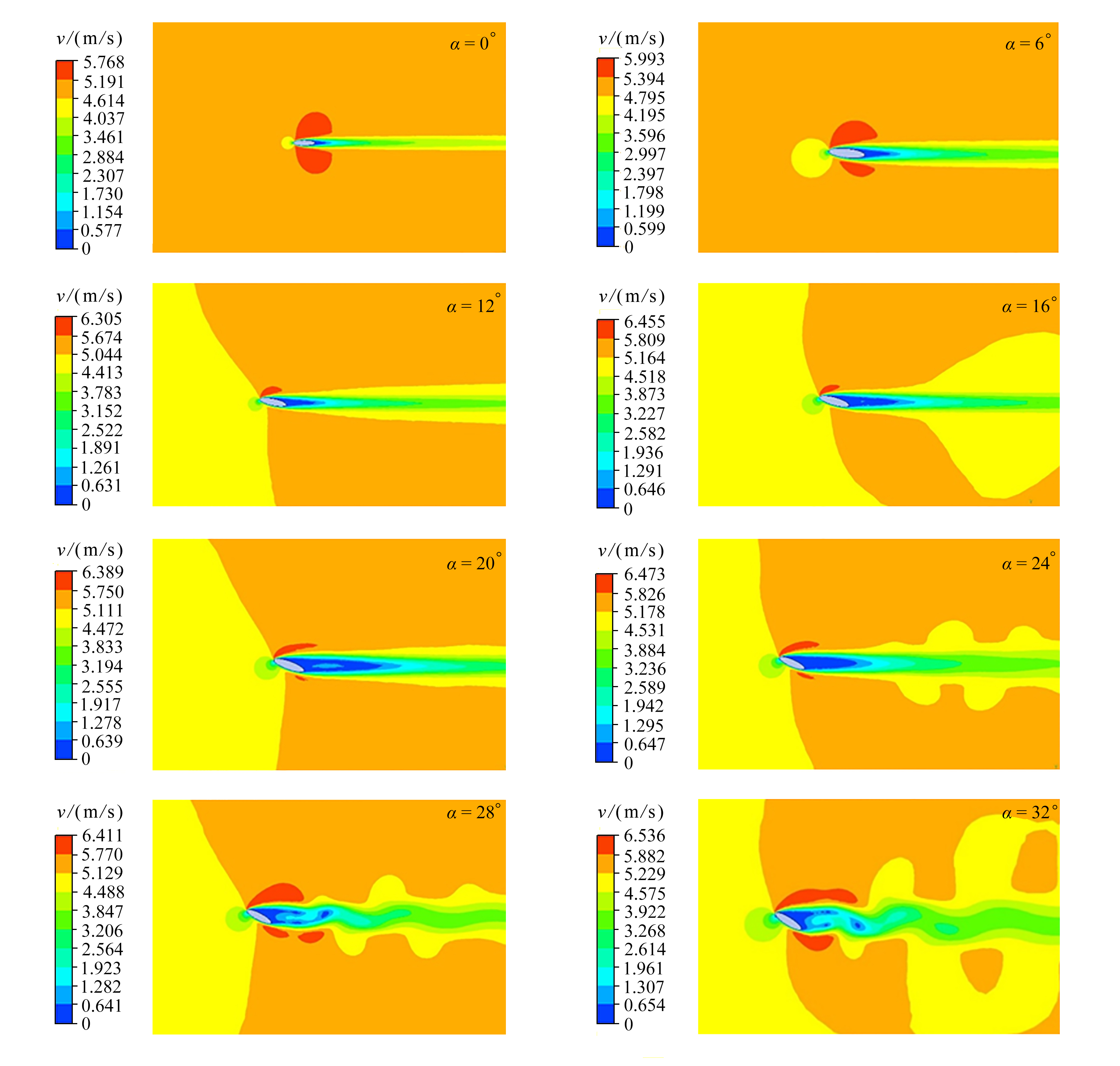
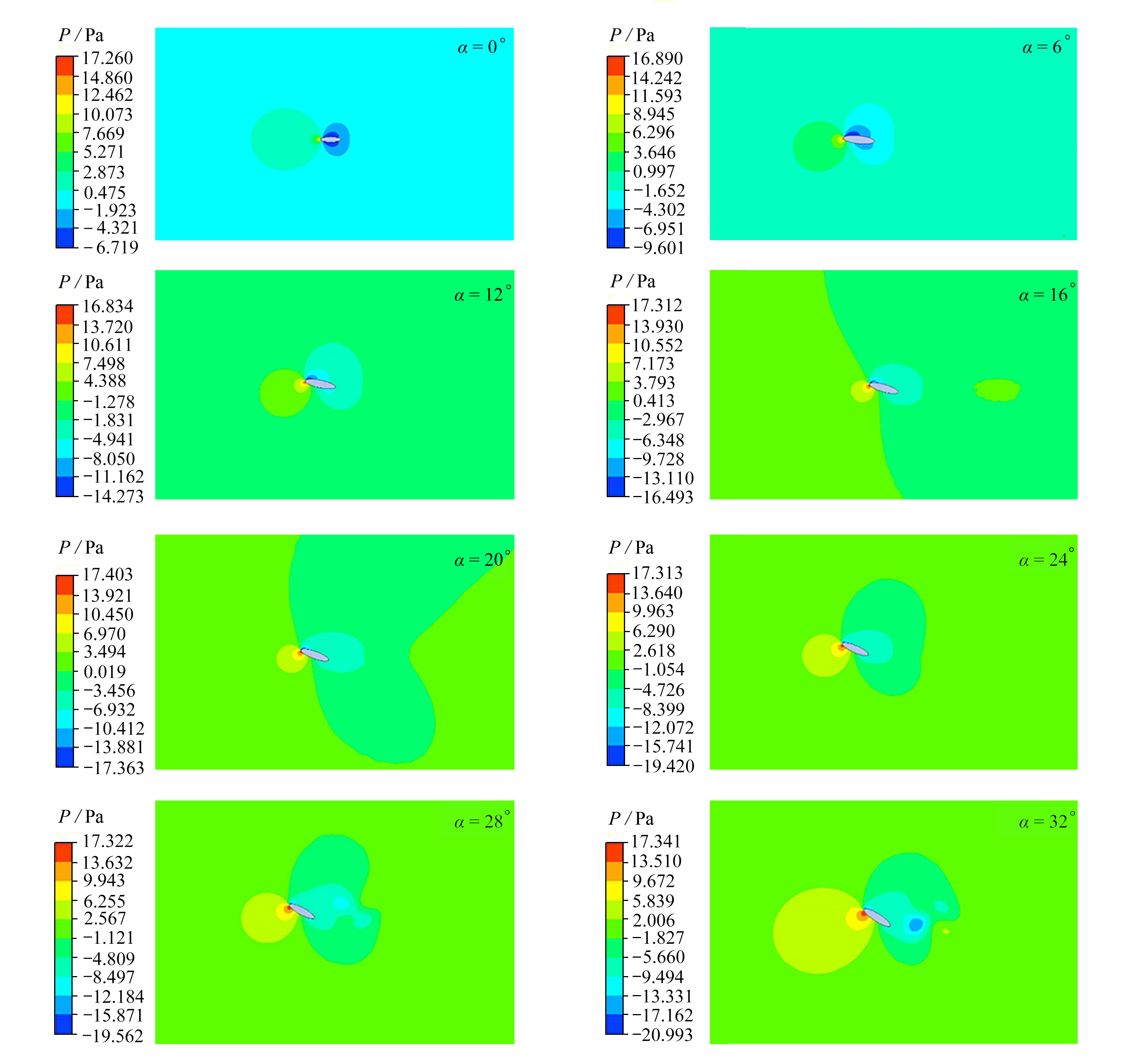
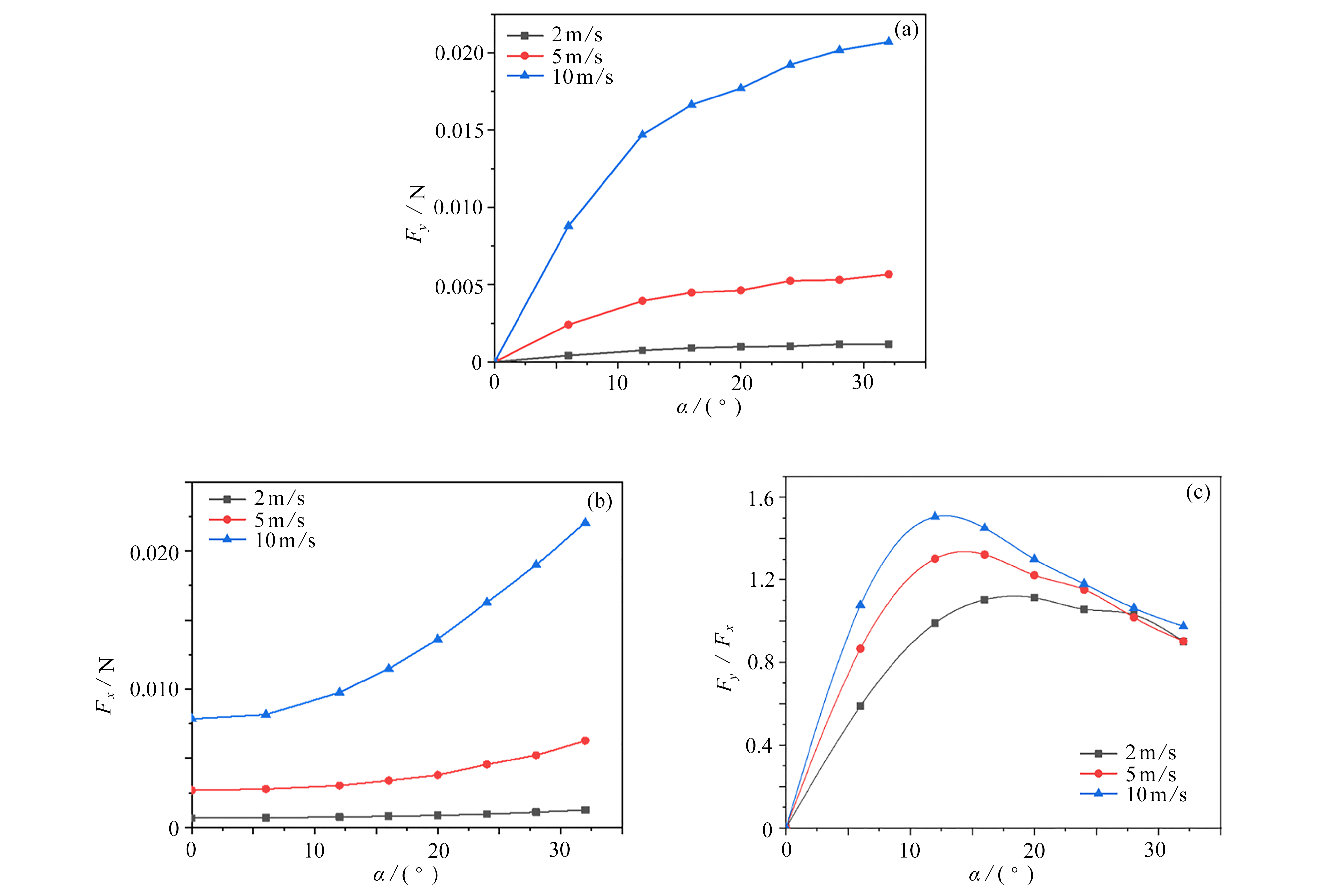
选取翼型迎角为0°,6°,12°,16°,20°,24°,28°,32°,风速为2 m/s,5 m/s,10 m/s,分别计算得到椭圆翼型周围的流场(图5),压力场(图6),升、阻力及升阻比(图7)。
从速度云图(图5)可以看出,随着攻角增大,椭圆翼型后流动分离范围逐渐增大。当迎角较小时,流动为稳定的层流;当迎角达到24°,翼型后的流动开始出现扰动;当迎角达到28°以上时,翼型后出现周期性的涡脱落。从不同迎角下的压力云图(图6)可以看出,当迎角增大到一定程度,由于脱落涡的出现,出现了脱离翼型的负压中心。
从升力曲线图(图7(a))可以看出,升力随来流风速的增大而增大;当迎角较小时,升力随迎角线性增大;随着迎角进一步增大,由于椭圆翼型后流动分离加剧,升力随迎角的增大呈非线性变化,迎角越大升力增大的速率越慢。从阻力曲线图(图7(b))可以看出,当迎角较小时,阻力随着迎角缓慢增大;当迎角增大达到16°左右时,阻力随迎角迅速增大。而升阻比随迎角变化成非单调趋势(图7(c)),随迎角的增大先增大再减小,当迎角为10°~15°时达到最大值。
2. 柔性翼型流固耦合仿真分析
2.1 流固耦合模型
在以上刚性翼计算模型的基础上,将椭圆翼型考虑为柔性翼。果蝇翅膀上分布着沿展向翅脉,且翅脉的刚度远大于翼面。为了简化模型,在柔性扑翼椭圆翼型模型中心的空心圆柱(直径为0.02 mm)面,采用固定边界,以模拟刚性翅脉(图8)。流体作用力与柔性翼型固体结构相互耦合,一方面流体在固体结构表面产生作用力,使固体结构产生变形;结构形状的改变,引起流场结构的改变。流固耦合仿真分析在ANSYS Workbench平台中用Fluent计算流体模块进行流场分析,用Transient Structural瞬态结构模块进行结构分析,使用System Coupling耦合求解器将两个模块关联起来,双向传递流体的计算数据和固体结构的计算数据,将流场与结构变形进行耦合。在流固耦合分析时,需要建立流固界面进行数据传递,因此柔性翼型模型应为三维模型。
柔性翼型固体结构分析的动力学控制方程[9]可写为
Mu′′+Cu′+Ku=F(t), (6) 式中
M ,C ,K 分别为质量矩阵、阻尼矩阵、刚度矩阵;F(t) 为流体作用在固体结构表面上的瞬态耦合力,其对结构的综合作用可以是力,也可以是力矩。柔性材料密度为1 000 kg/m3 ,材料本构模型采用线弹性模型,Poisson比为0.3,弹性模量可调。2.2 网格划分
流固耦合计算在Fluent中采用动网格技术,采用非结构网格进行划分。在流固耦合计算中,当固体结构发生变形后,流场需要接收固体变形的位移数据,流场边界也相应的改变,因此需要使用动网格进行网格重构。具体为在Dynamic Mesh中设置Smoothing与Remeshing,将椭圆壁面设为System Coupling,端部壁面设为Deforming,其余设置与刚性翼型一致。固体结构也采用非结构网格进行划分。
2.3 模型验证
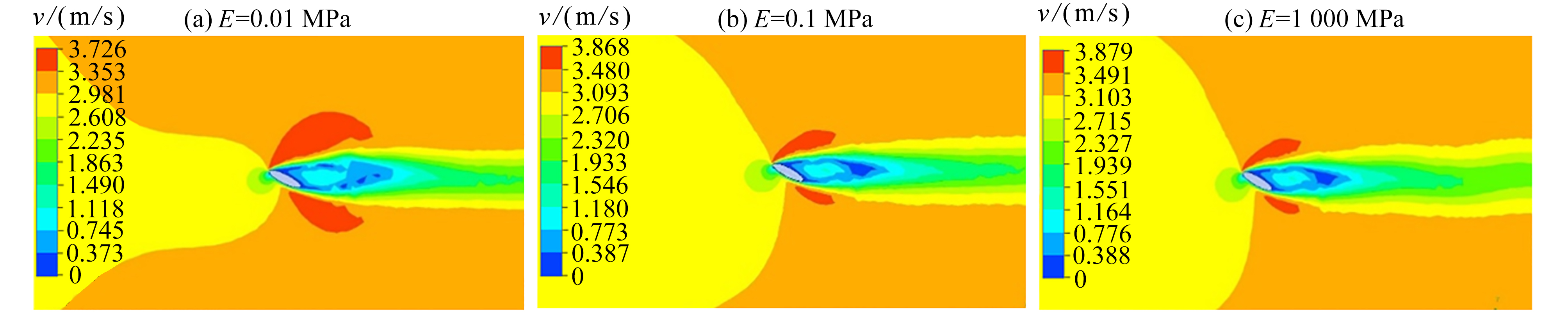
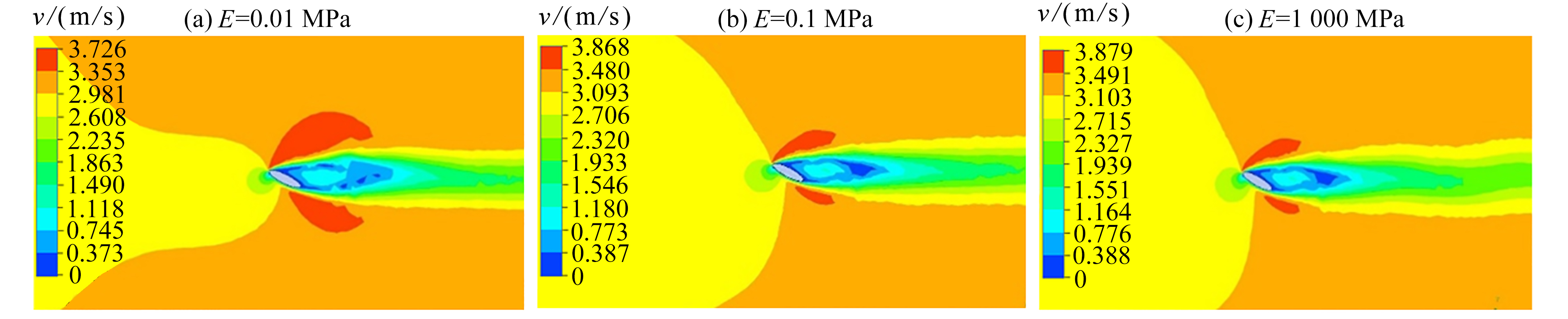
在验证模型中,椭圆翼型迎角设置为27.5°,来流速度为2.94 m/s。柔性翼型弹性模量为0.01 MPa,0.1 MPa,1000 MPa,分析流固耦合模型的流场和固体结构变形。
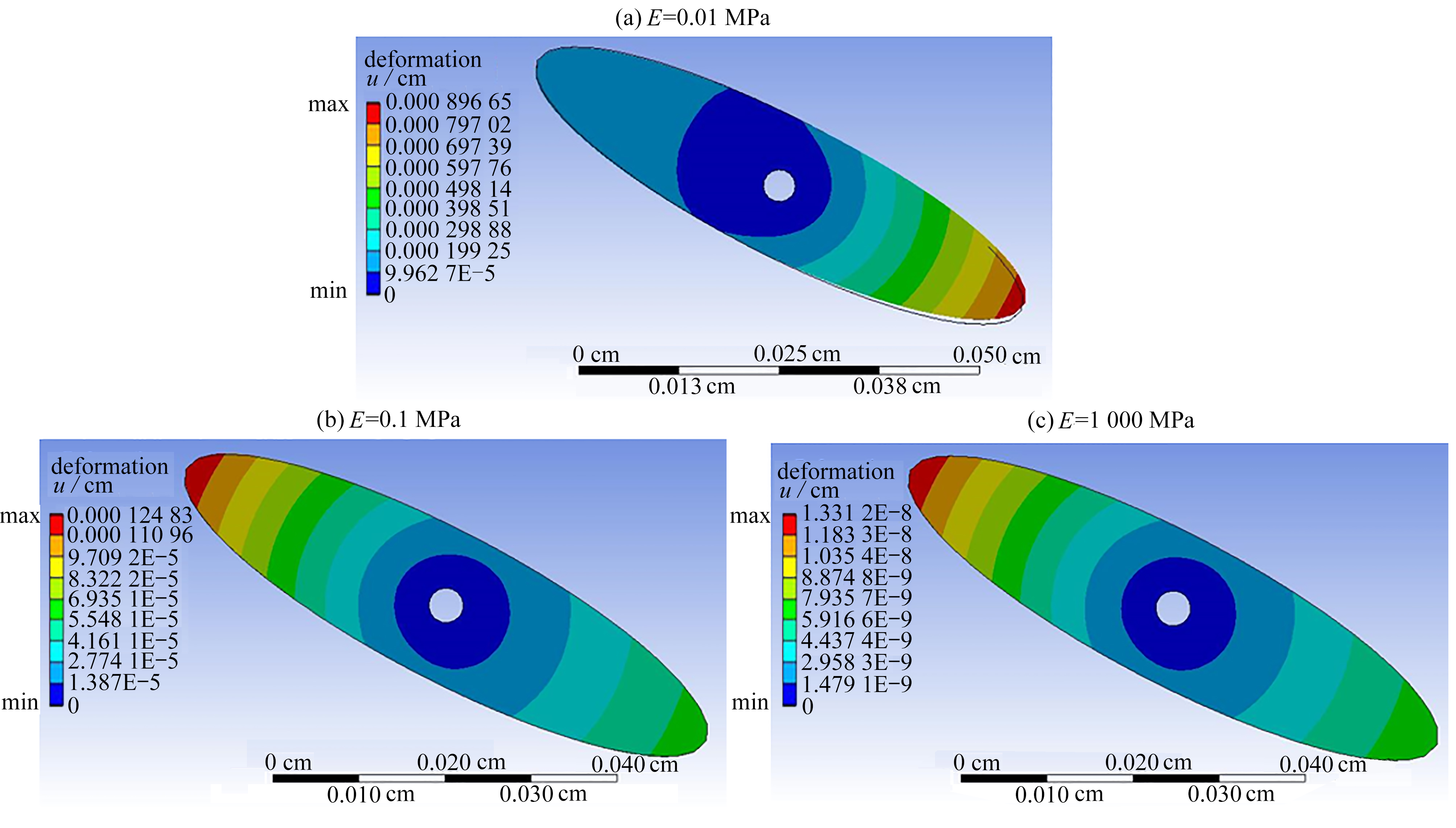
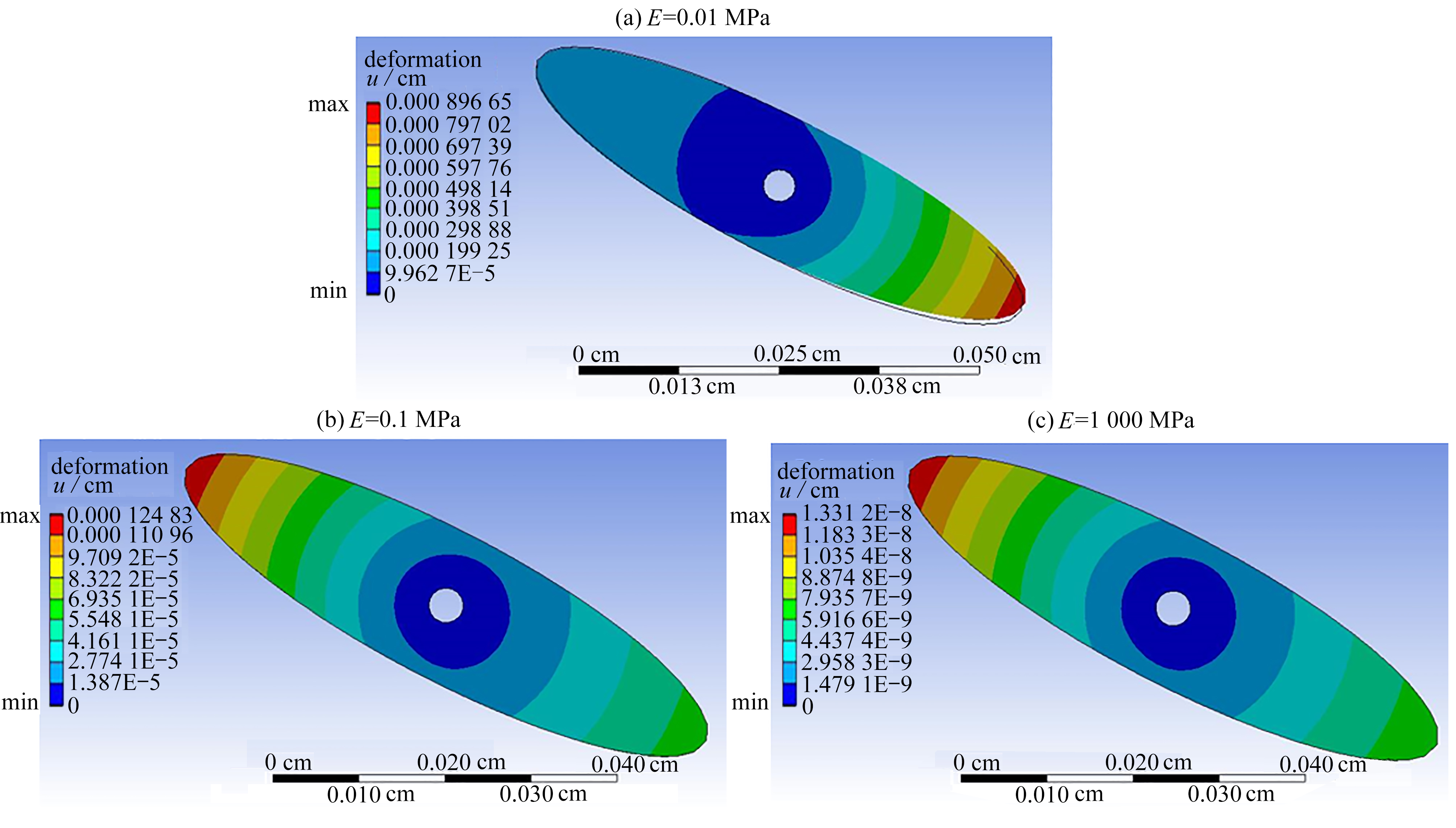
从翼型周围流场速度云图(图9)可以看出,随着椭圆翼型弹性模量的减小,翼型周围的最大流速减小,但是翼型对周围流场的扰动范围扩大。类似地,从翼型周围流场压力云图(图10)可以看出,随着椭圆翼型弹性模量的减小,翼型周围产生的最大负压值减小,但是翼型周围的负压区扩大。从柔性翼型结构位移云图(图11)可以看出,随着椭圆翼型弹性模量的减小,柔性翼型结构位移增大。
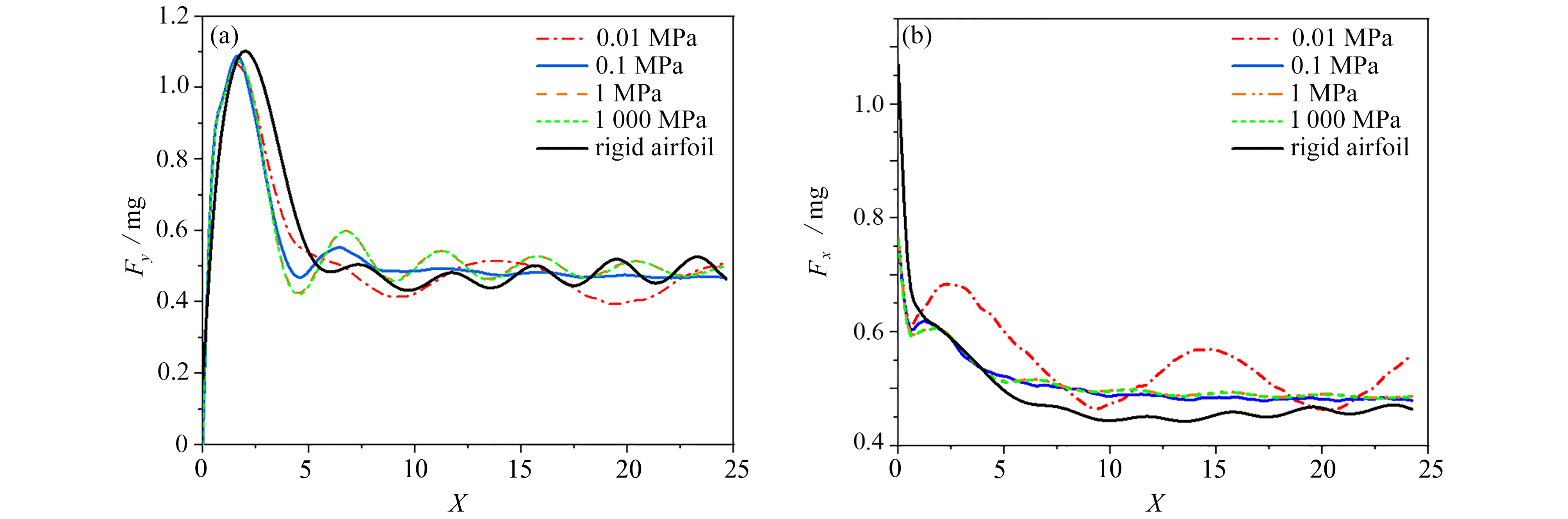
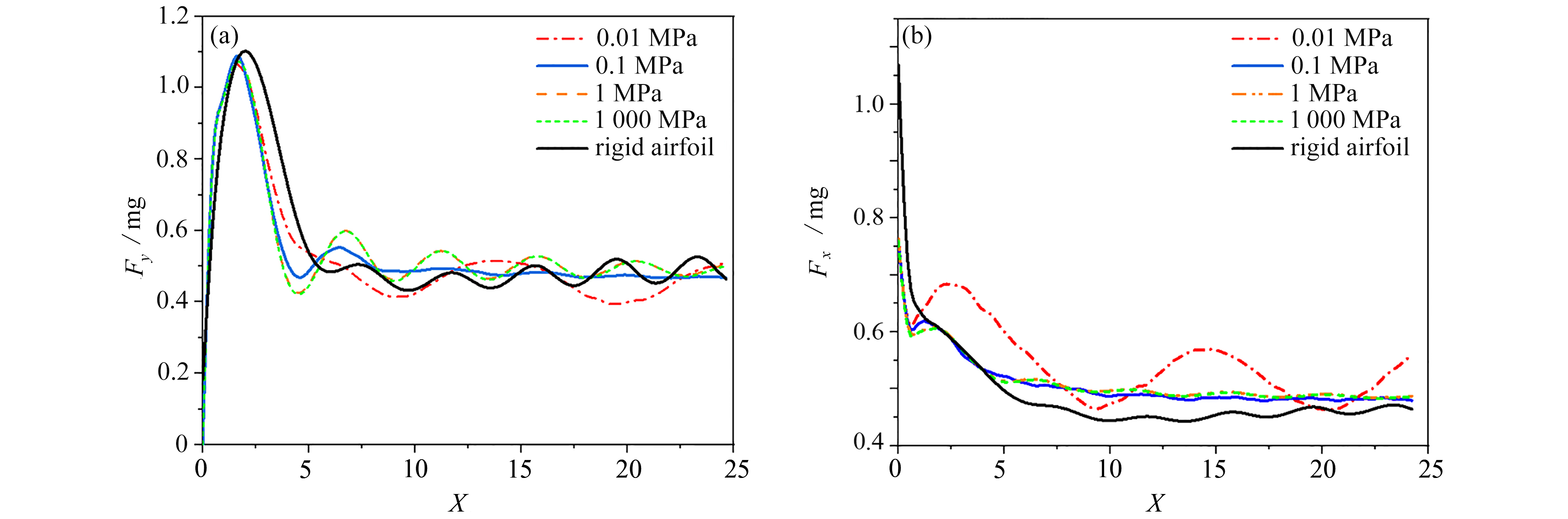
从升力曲线图(图12(a))可以看出,柔性椭圆翼型升力开始阶段由于求解过程未收敛出现较大幅度波动,随后升力值稳定在0.4~0.6 mg之间呈现出周期性变化,总体变化趋势与刚性翼型一致。但随着弹性模量的降低,升力值稳定扰动振荡的周期增大。而随着弹性模量的降低,扰动振荡的振幅呈先减小再增大的趋势。当弹性模量降低到0.1 MPa时,升力值扰动振荡幅度几乎消失,升力值达到一稳定值(约0.5 mg);而当弹性模量进一步降低时,升力值又呈现出周期性的震荡变化。由此可见,较刚性翼型,柔性翼型对于稳定升力扰动有着积极的作用。类似地,从阻力曲线图(图12(b))中可以看出,较刚性翼型,柔性翼型的阻力略大于刚性翼。且随着弹性模量的降低,柔性翼型的阻力逐渐出现了周期性振荡。
2.4 不同迎角下流场及气动性能
柔性翼型的迎角分别选取0°,6°,12°,16°,20°,24°,28°,32°进行仿真分析。风速为5 m/s,柔性翼型弹性模量为0.1 MPa。
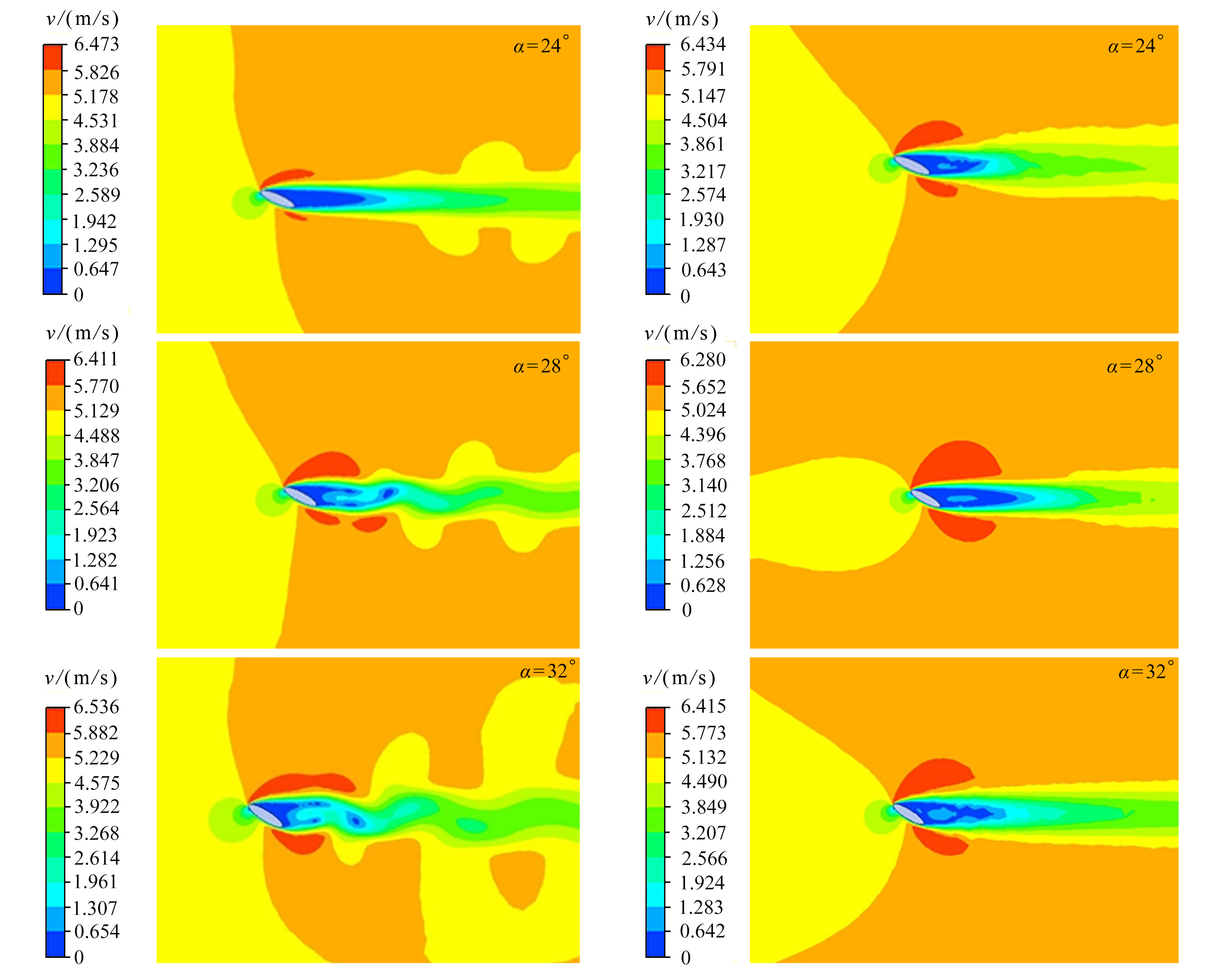
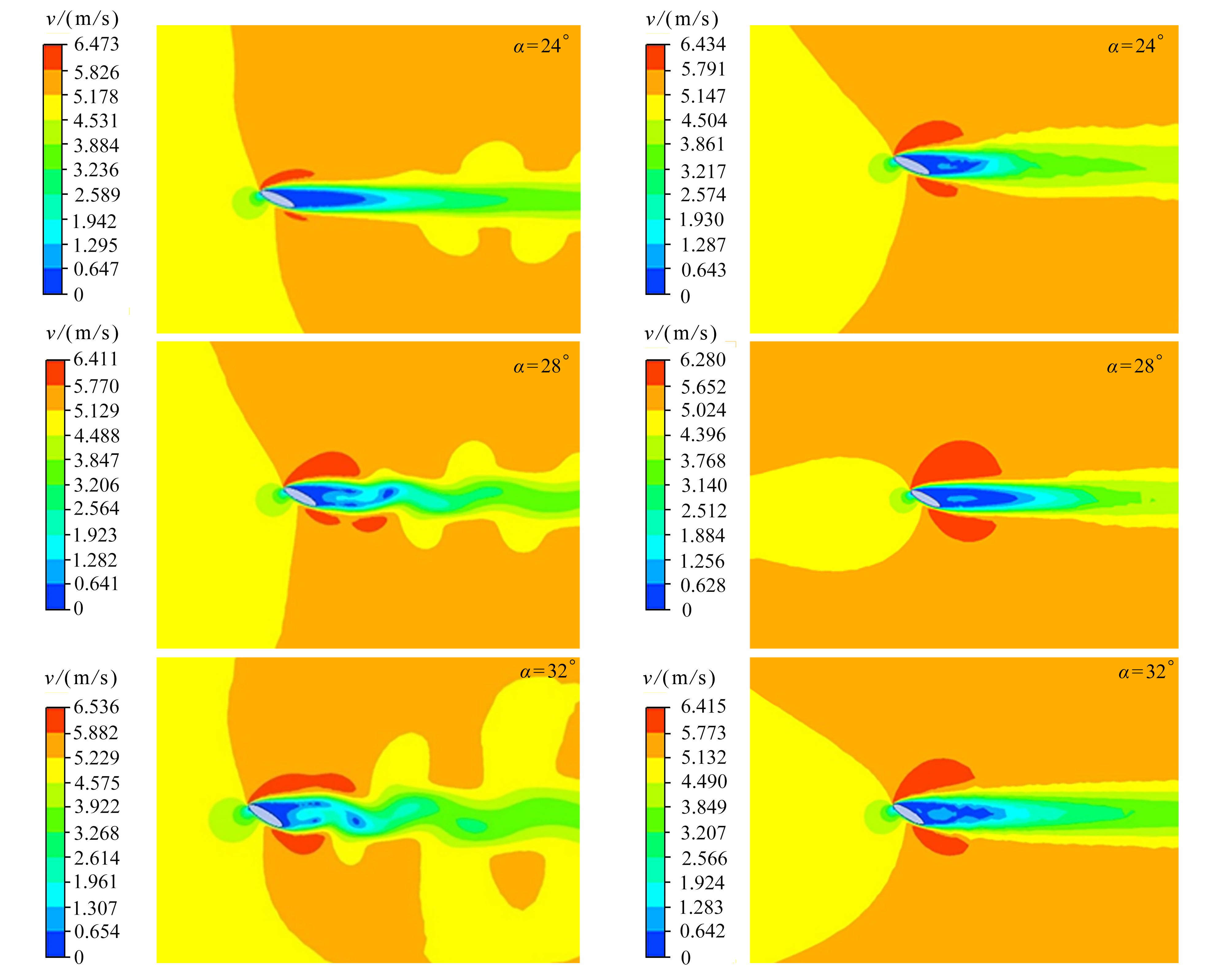
由翼型周围流场(图13)可以看出,随着迎角逐渐增大,刚性翼型后的流场逐渐出现扰动,翼型后伴随有尾涡脱落。而柔性翼型后的流场与刚性翼型有很大不同,流体流过柔性翼型后尽管出现了流动分离,但流场并未出现明显的扰动。由此可见,较刚性翼型,柔性翼型延缓了尾涡脱落时间,显著抑制了尾流流场的扰动范围及幅度。
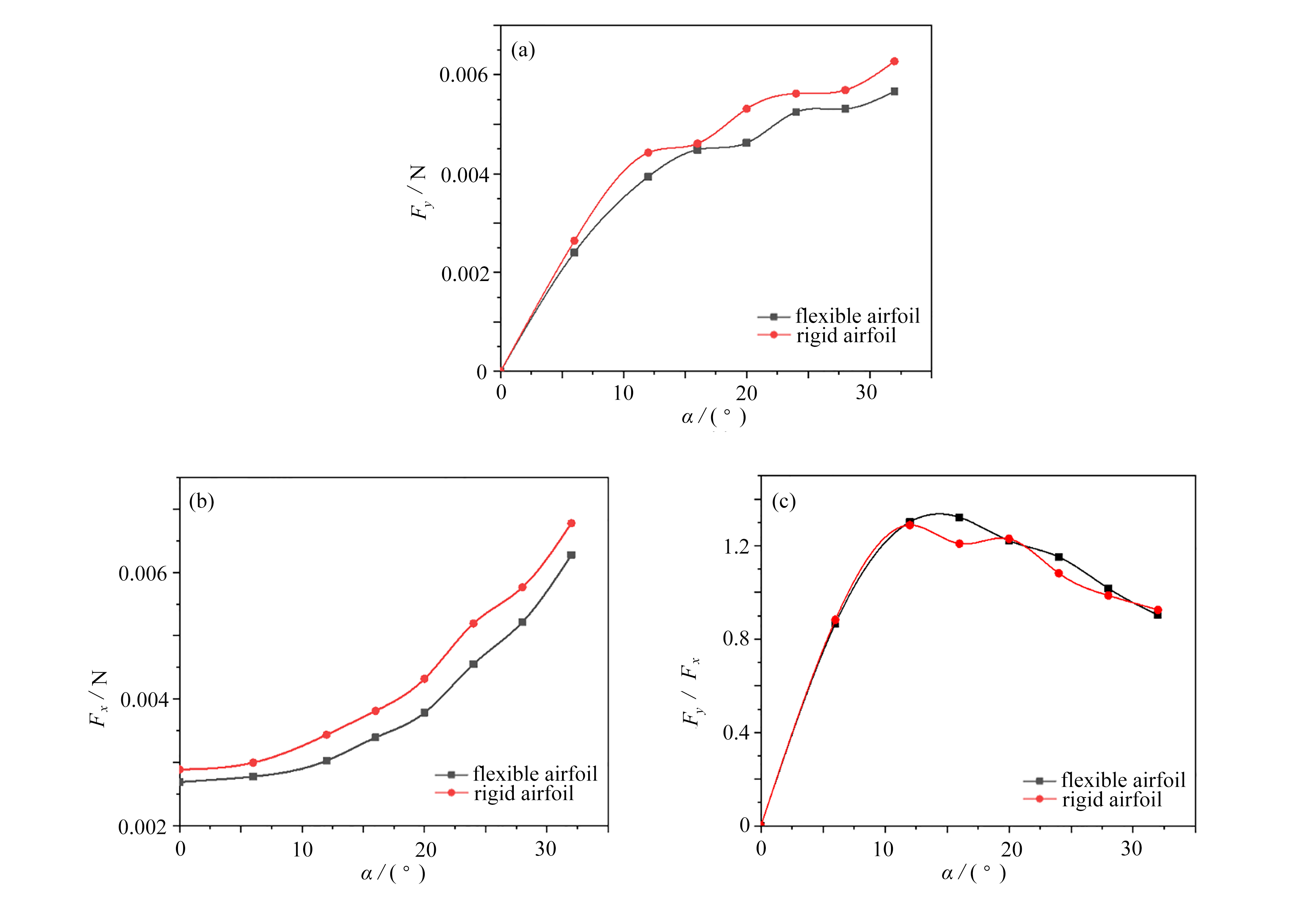
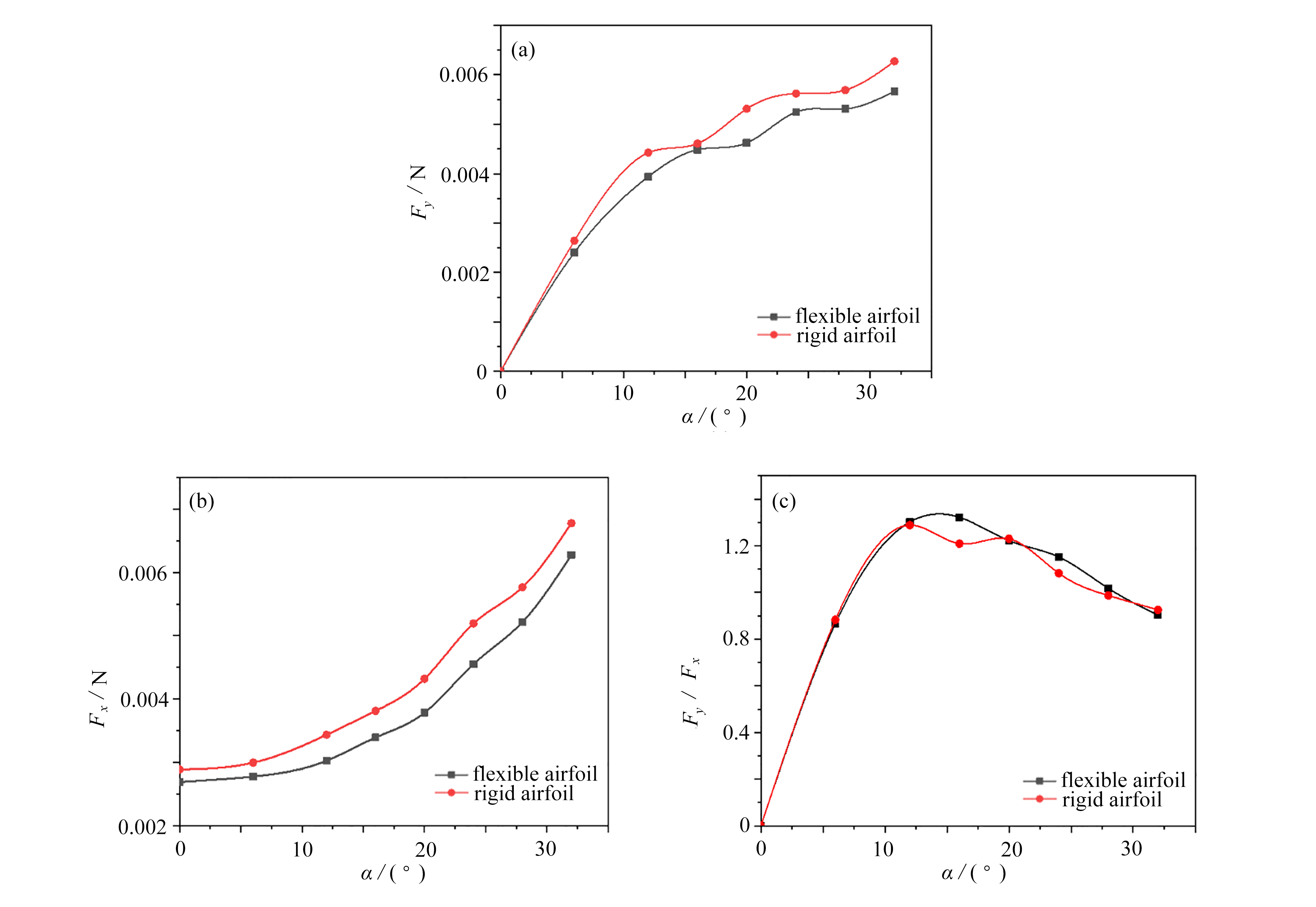
由柔性翼型的升力曲线(图14(a))可以看出,升力随着迎角增大而增大,且柔性翼型的升力略大于刚性翼型。由柔性翼型的阻力曲线(图14(b))可以看出,阻力随迎角的增大而增大,且柔性翼型的阻力略大于刚性翼型。但从升阻比(图14(c))看,柔性翼型与刚性翼型并无相显著差异。也就是说,柔性翼型并未损失飞行效率。
3. 结 论
本文从仿生学的角度出发,通过流固耦合数值仿真分析了柔性翼型在不同风速、迎角下的空气动力学特性。研究发现,较刚性翼型,柔性翼型延缓了尾涡脱落时间,有效降低升力扰动振荡频率;柔性翼型显著抑制了尾流流场的扰动,降低升力扰动振荡幅值,合适的弹性模量翼型使得扰动振荡完全消除,这将有利于改善飞行器运动平顺性、降低气动噪声。
致谢 本文作者衷心感谢江苏省仿生功能材料重点实验基金对本文的资助。
-
-
[1] 孙茂, 吴江浩. 昆虫飞行的高升力机理和能耗[J]. 北京航空航天大学学报, 2003, 29(11): 970-977. (SUN Mao, WU Jianghao. Unsteady lift mechanisms and energetic in flying insects[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(11): 970-977.(in Chinese) doi: 10.3969/j.issn.1001-5965.2003.11.004 [2] ELLINGTON C P, BERG C V D, WILLMOTT A P, et al. Leading-edge vortices in insect flight[J]. Nature, 1996, 384(6610): 626-630. doi: 10.1038/384626a0 [3] DICKINSON M H, LEHMANN F O, SANE S P. Wing rotation and the aerodynamic basis of insect flight[J]. Science, 1999, 284(5422): 1954-1960. doi: 10.1126/science.284.5422.1954 [4] TANG J, VIIERU D, SHYY W. A study of aerodynamics of low Reynolds number flexible airfoils[C]//37th AIAA Fluid Dynamics Conference and Exhibit. Miami, USA, 2007. [5] VISBAL M R, GORDNIER R E, GALBRAITH M C. High-fidelity simulations of moving and flexible airfoils at low Reynolds numbers[J]. Experiments in Fluids, 2009, 46(5): 903-922. doi: 10.1007/s00348-009-0635-4 [6] 张兴伟, 周超英, 谢鹏. 扑翼柔性变形对悬停气动特性影响的数值研究[J]. 哈尔滨工业大学学报, 2012, 44(1): 115-119.ZHANG Xingwei, ZHOU Chaoying, XIE Peng. Numerical study on the effect of flapping wing deformation on aerodynamic performance in hovering flight[J]. Journal of Harbin Institute of Technology, 2012, 44(1): 115-119. (in Chinese) [7] 王姝歆, 周建华, 颜景平. 微小型仿生飞行机器人柔性翅的仿生设计与实验研究[J]. 实验流体力学, 2006, 20(1): 75-79. (WANG Shuxin, ZHOU Jianhua, YAN Jingping. Bionic design and experiment on flexible wings of a bionic flying micro-robot[J]. Journal of Experiments in Fluid Mechanics, 2006, 20(1): 75-79.(in Chinese) doi: 10.3969/j.issn.1672-9897.2006.01.018 [8] KANG W, ZHANG J Z, LEI P F, et al. Computation of unsteady viscous flow around a locally flexible airfoil at low Reynolds number[J]. Journal of Fluids and Structures, 2014, 46: 42-58. doi: 10.1016/j.jfluidstructs.2013.12.010 [9] 陶真新, 李绍斌, 宋西镇. 低雷诺数下柔性翼型气动性能分析[J]. 力学与实践, 2017, 39(2): 145-151.TAO Zhenxin, LI Shaobin, SONG Xizhen. The aerodynamic performance of a flexible airfoil at low Reynolds number[J]. Mechanics in Engineering, 2017, 39(2): 145-151. (in Chinese) [10] PESAVENTO U, WANG Z J. Flapping wing flight can save aerodynamic power compared to steady flight[J]. Physical Review Letter, 2009, 103(11): 118102. doi: 10.1103/PhysRevLett.103.118102 [11] 杨金广, 吴虎. 双方程k-ω SST湍流模型的显式耦合求解及其在叶轮机械中的应用[J]. 航空学报, 2014, 35(1): 116-124. (YANG Jinguang, WU Hu. Explicit coupled solution of two-equation k-ω SST turbulence model and its application in turbomachinery flow simulation[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 116-124.(in Chinese) [12] MENTER F R. Zonal two equation k-ω turbulence models for aerodynamic flows[C]//AIAA 23rd Fluid Dynamics, Plasmadynamics, and Leaders Conference. Orlando, USA, 1993. 期刊类型引用(4)
1. 刘勇岗,苏丽君. 流-固耦合作用下小尺寸肾结石引发的输尿管疼痛响应. 应用数学和力学. 2024(06): 735-752 .  本站查看
本站查看2. 赵香宁,曾鹏飞,郝永平. 材料属性对柔性仿生扑翼气动特性的影响. 机械工程与自动化. 2024(05): 29-31 .  百度学术
百度学术3. 薛纭,陈立群. 弹性薄壳动力学比拟的曲面论基础. 应用数学和力学. 2023(05): 489-498 .  本站查看
本站查看4. 岳欠杯,王笑笑,曹文,刘跃秋,李辉,徐燕璐. 基于嵌套网格的环空流体内旋转杆柱与井筒碰撞特性研究. 应用数学和力学. 2023(05): 543-559 .  本站查看
本站查看其他类型引用(1)
-





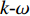

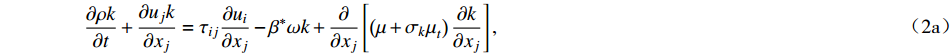
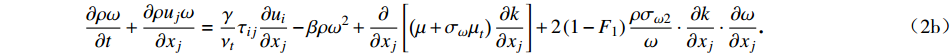

 下载:
下载:



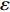
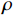
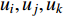
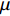
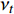
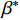
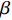
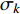
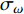
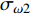


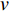
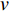
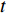
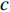
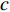





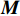

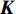








 下载:
下载:





 渝公网安备50010802005915号
渝公网安备50010802005915号