Investigation on the 2D Contact of Multilayer Functionally Graded Piezoelectric Material Coating Under Conducting Indenters
-
摘要:
考虑了材料参数可按照任意函数形式变化的功能梯度压电材料(FGPM)涂层在不同形状导电压头作用下的接触问题，研究了梯度系数对功能梯度压电涂层接触力学行为的影响。建立了多层功能梯度压电材料涂层模型，运用了Fourier积分变换和传递矩阵将多层功能梯度压电材料涂层的接触问题转化为奇异积分方程。利用Gauss-Chebyshev数值计算方法，得到了多层功能梯度压电材料涂层-基底结构在刚性导电平压头和圆柱形压头作用下的表面应力分布和电荷分布。利用数值解，分析了材料参数按照不同变化形式的FGPM涂层对最大压痕和电势的影响，还分析了功能梯度压电涂层内部的应力和电位移分布。研究结果表明，功能梯度压电材料参数的不同变化形式对结构的接触性能具有重要的影响。
-
关键词:
- 接触问题 /
- FGPM涂层 /
- 导电压头 /
- Fourier积分变换 /
- 奇异积分方程
Abstract:In view of the contact problem of functionally graded piezoelectric material (FGPM) coating under different kinds of conducting indenters, effects of the gradient index on the contact mechanical behavior of the FGPM coating were investigated. A model for the multilayer FGPM coating was established. The contact problem of the FGPM coating was transformed into singular integral equations by means of the Fourier integral transform technology and the transfer matrix method. The Gauss-Chebyshev quadrature formula was used to obtain the surface stress distribution and the charge distribution in the FGPM coating-substrate system under a rigid conducting flat indenter and a conducting cylindrical indenter. According to the numerical results, the effects of variations of the FGPM coating parameters on the indentation and electrical potential were analyzed. The distributions of stress and electrical displacement in the FGPM coating were obtained. The results show that, the variations of the FGPM coating parameters have an important influence on the contact behavior of the system.
-
图 1 法向集中线载荷P和正集中线电荷Q作用在FGPM涂层半平面
Figure 1. The FGPM coated half-plane subjected to normal concentrated line load P and positive concentrated line electric charge Q
图 2 多层功能梯度压电涂层模型
Figure 2. The multi-layer model for the functional gradient piezoelectric coating
图 3 FGPM涂层-基底结构与刚性导电压头的无摩擦接触
Figure 3. Frictionless contact between an FGPM coated half-plane and a conducting rigid indenter
图 4 FGPM涂层与导电平压头的无摩擦接触问题
Figure 4. The frictionless contact problem between the FGPM coated half-plane and the conducting flat indenter
图 5 FGPM涂层与导电圆柱压头的无摩擦接触问题
Figure 5. The frictionless contact problem between the FGPM coateded half-plane and the conducting cylindrical indenter
图 6 应力分布
$p\left( x \right)$ 和电荷分布$q\left( x \right)$ 求解过程的流程图Figure 6. The flowchart for the procedure of solution to obtain stress distribution
$p\left( x \right)$ and charge distribution$q\left( x \right)$ 
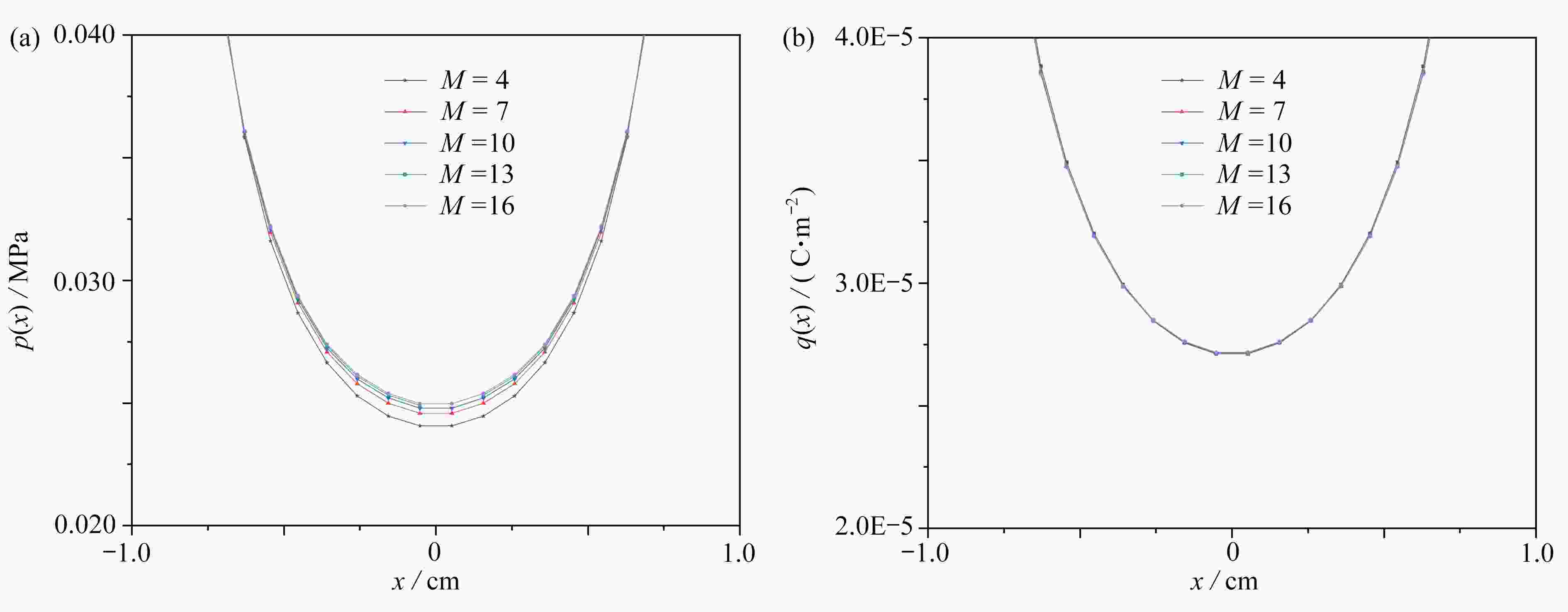
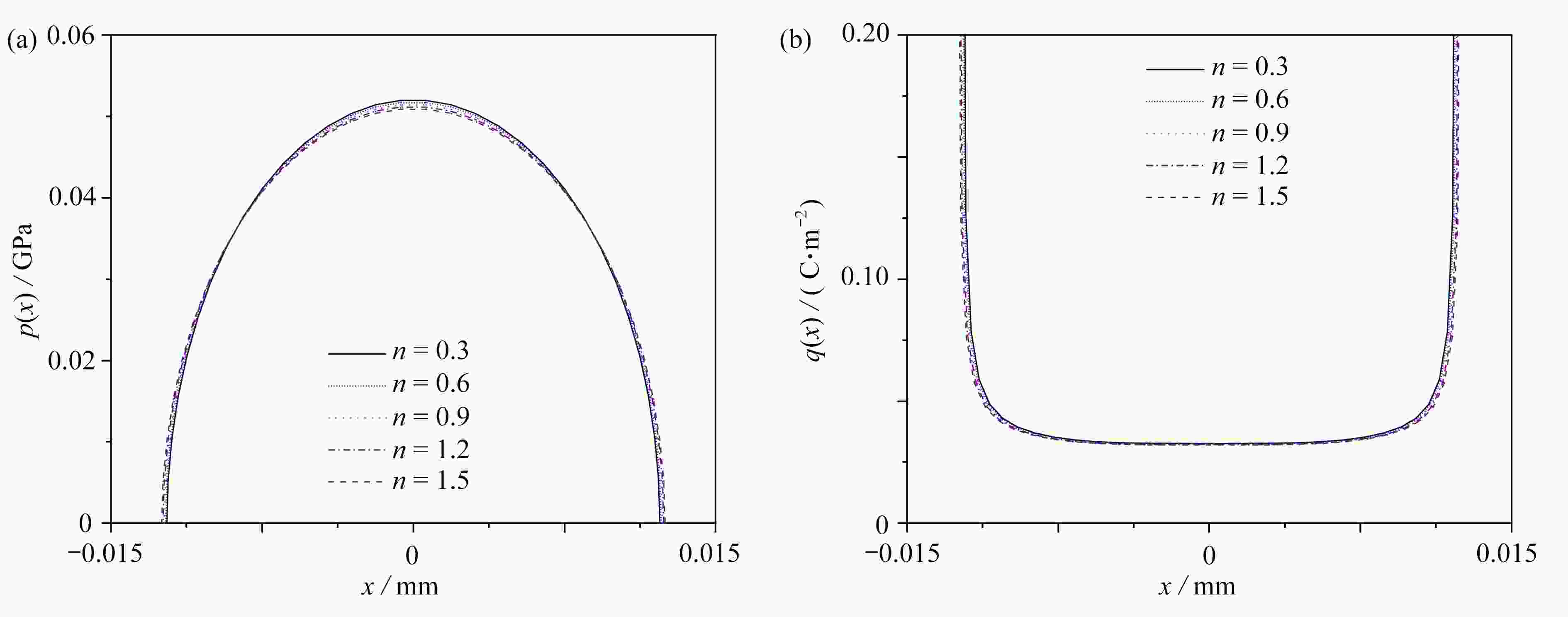
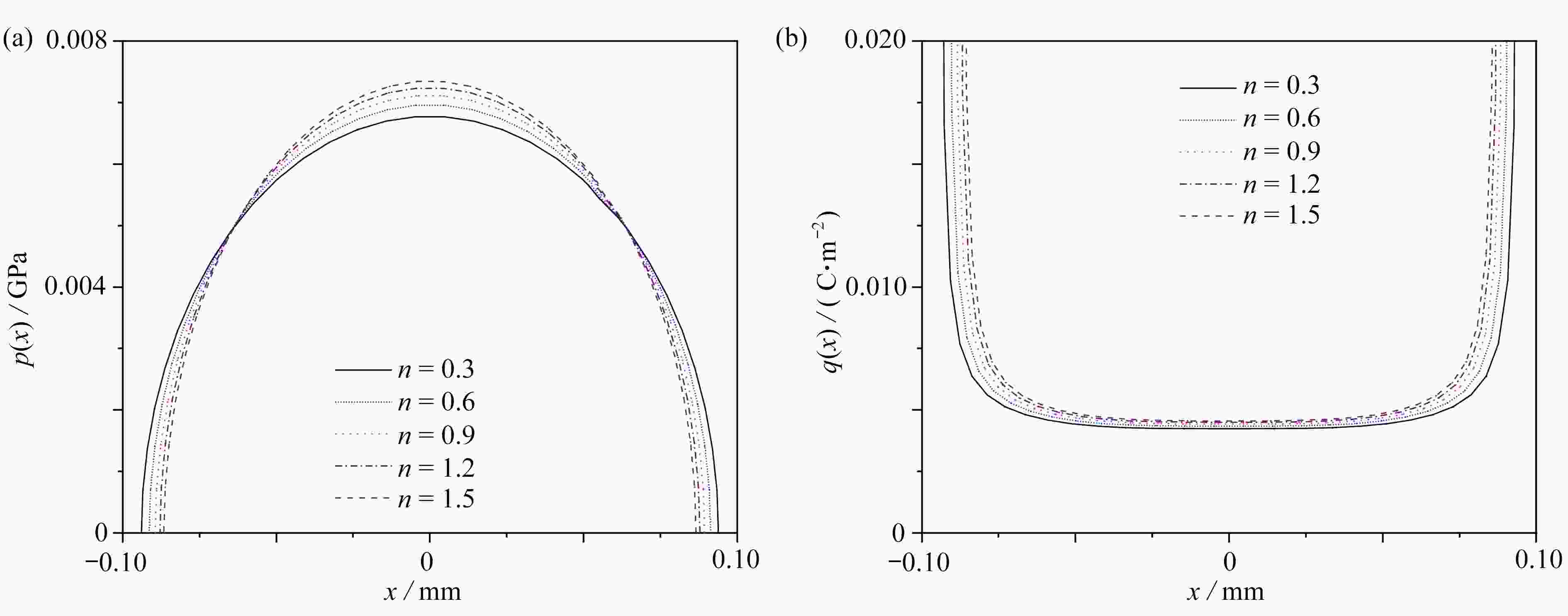
图 7 不同分层数对多层压电材料涂层在导电平压下的压力分布
$p\left( x \right)$ 和电荷分布$q\left( x \right)$ 的影响注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同。
Figure 7. Effects of the number of layers on pressure distribution
$p\left( x \right)$ and the charge distribution$q\left( x \right)$ of the multi-layer piezoelectric model under the conducting flat indenter
图 10
$k = 8/1$ 时，导电平压头作用下的梯度指数$n$ 对接触应力$p\left( x \right)$ 和电荷分布$q\left( x \right)$ 的影响Figure 10. Effects of gradient index
$n$ on distribution of contact stress$p\left( x \right)$ and electric charge$q\left( x \right)$ under the conducting flat indenter for$k = 8/1$ 
图 11
$k = 1/8$ 时，导电平压头作用下的梯度指数$n$ 对接触应力$p\left( x \right)$ 和电荷分布$q\left( x \right)$ 的影响Figure 11. Effects of gradient index
$n$ on distribution of contact stress$p\left( x \right)$ and electric charge$q\left( x \right)$ under the conducting flat indenter for$k = 1/8$ 
图 12
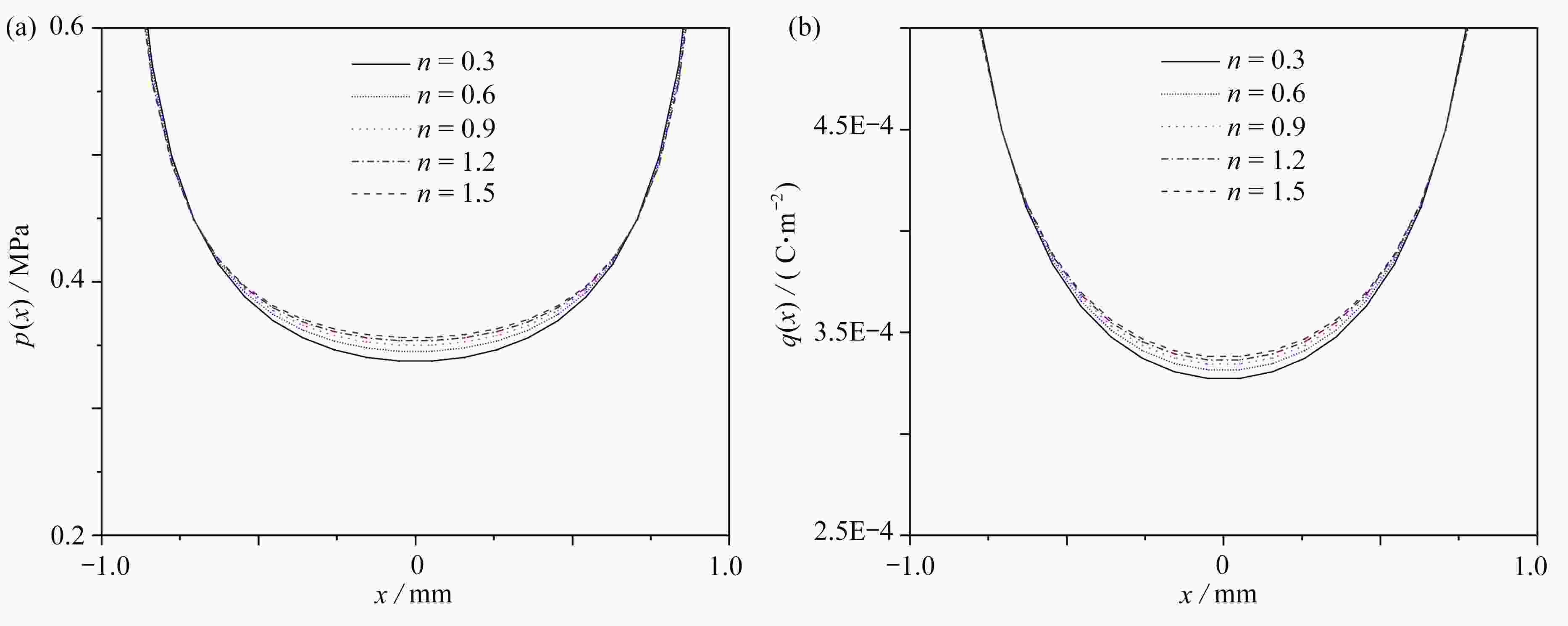
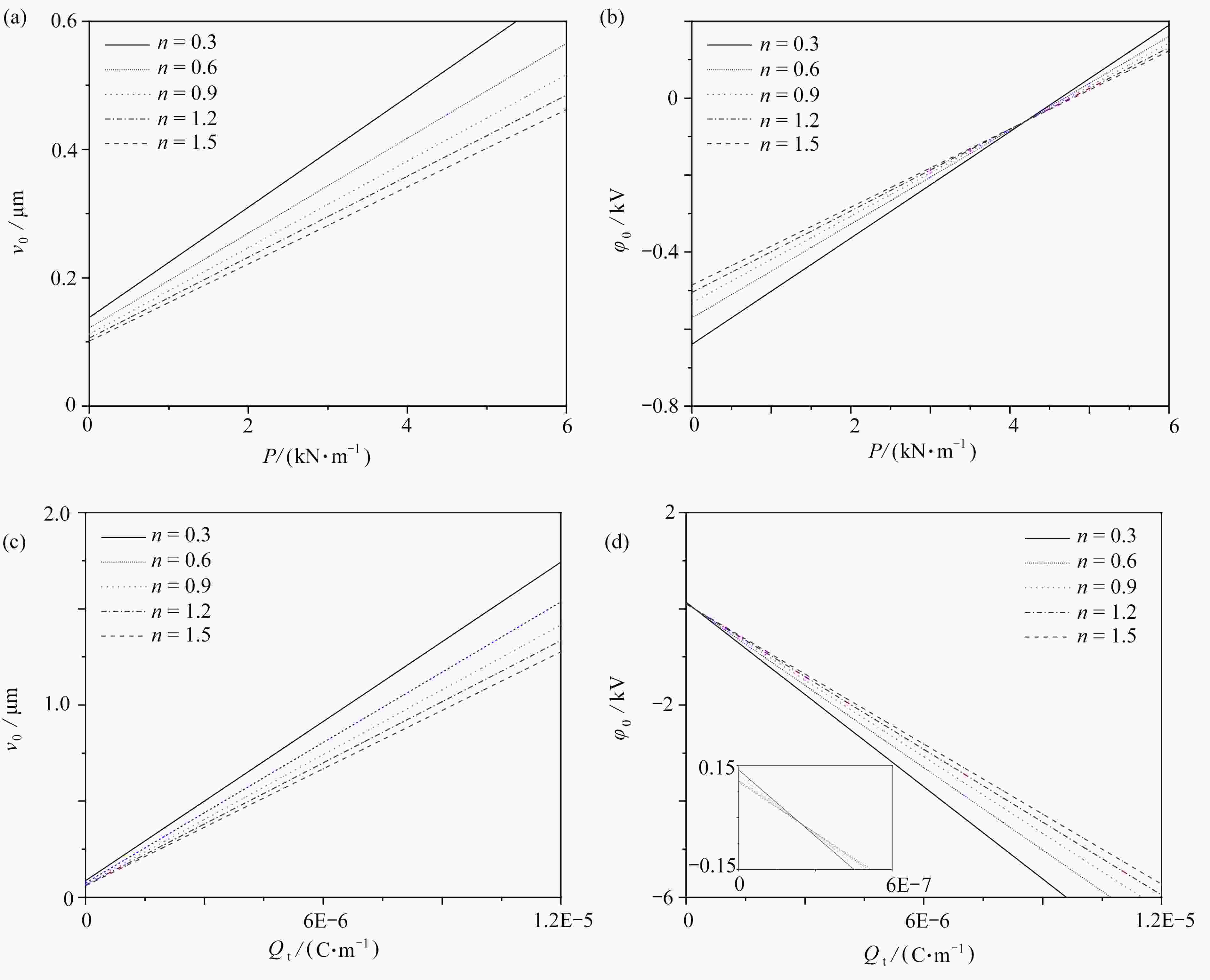
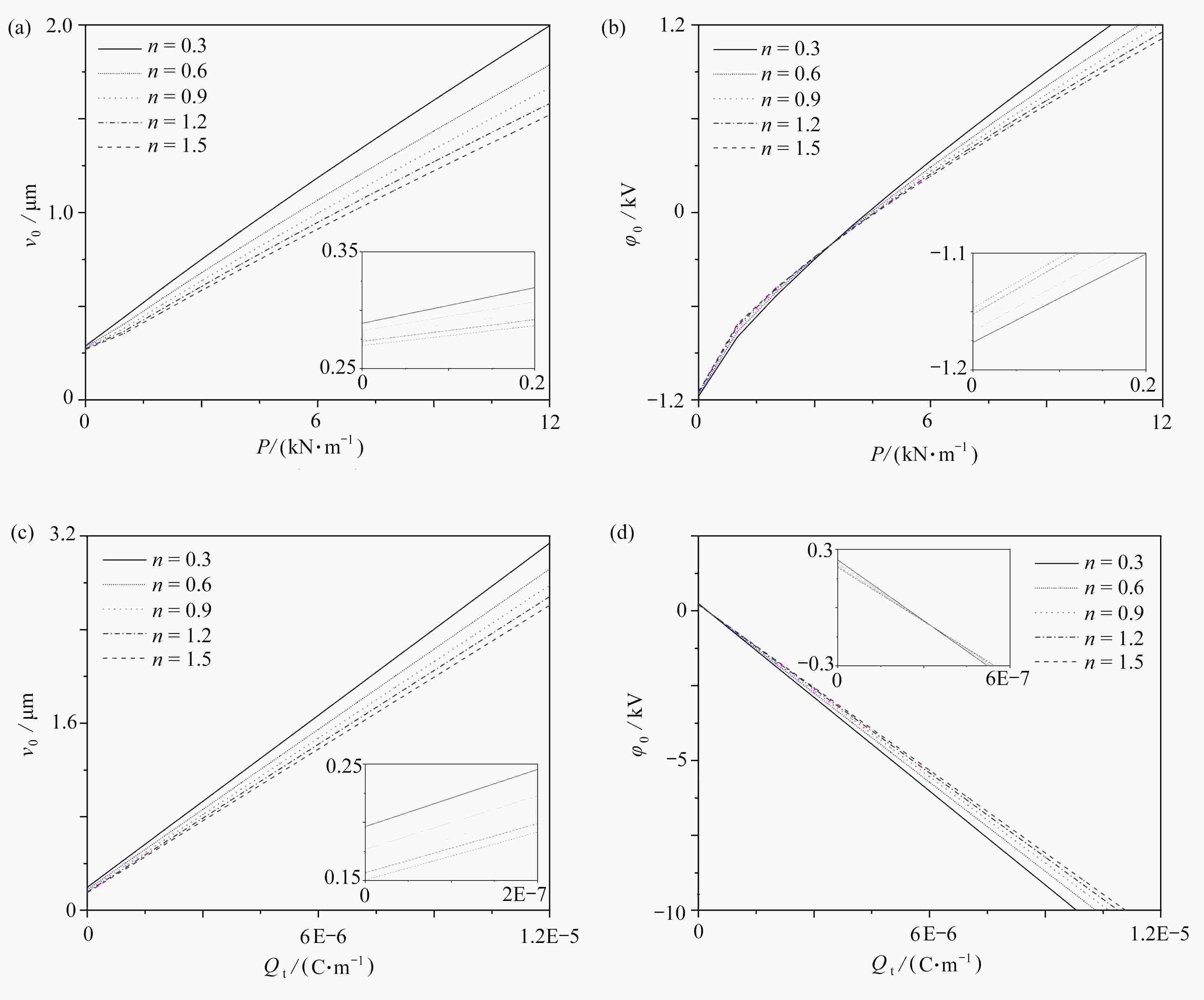
$k = 8/1$ 时，$n$ 值变化对压力与压痕曲线、压力与电势曲线、电荷与位移曲线和电荷与电势曲线的影响Figure 12. Effects of
$n$ on the curve of applied force vs. indentation, the curve of applied force vs. electrical potential, the curve of electric charge vs. indentation and the curve of electrical charge vs. the electrical potential for$k = 8/1$ 
图 13
$k = 1/8$ 时，$n$ 值变化对压力与压痕曲线、压力与电势曲线、电荷与位移曲线和电荷与电势曲线的影响Figure 13. Effects of
$n$ on the curve of applied force vs. indentation, the curve of applied force vs. electrical potential, the curve of electric charge vs. indentation and the curve of electrical charge vs. the electrical potential for$k = 1/8$ 
图 14 当
$k = 8/1$ 时，$n$ 值变化对界面处($z = 0$ )竖向应力分布${\sigma _z}$ 和电位移${D_z}$ 的影响Figure 14. Effects of
$n$ on vertical stress distribution${\sigma _z}$ and electric displacement${D_z}$ at interface ($z = 0$ ) for$k = 8/1$ 
图 15 当
$k = 1/8$ 时，$n$ 值变化对界面处($z = 0$ )竖向应力分布${\sigma _z}$ 和电位移${D_z}$ 的影响Figure 15. Effects of
$n$ on vertical stress distribution${\sigma _z}$ and electric displacement${D_z}$ at interface ($z = 0$ ) for$k = 1/8$ 
图 16 当
$k = 8/1$ 时，$n$ 值变化对沿涂层厚度方向($x = 0$ )的应力${\sigma _z}$ 和电位移${D_z}$ 的影响Figure 16. Effects of
$n$ on stress${\sigma _z}$ and electrical displacement${D_z}$ at$x = 0$ along the thickness direction of coating for$k = 8/1$ 
图 17 当
$k = 1/8$ 时，$n$ 值变化对沿涂层厚度方向($x = 0$ )的应力${\sigma _z}$ 和电位移${D_z}$ 的影响Figure 17. Effects of
$n$ on stress${\sigma _z}$ and electrical displacement${D_z}$ at$x = 0$ along the thickness direction of coating for$k = 1/8$ 
图 18 在
$k = 8/1$ 和$k = 1/8$ 的情况下，$n$ 值对$P {\text{-}} a$ 关系图的影响Figure 18. Effects of
$n$ on relation$P$ vs.$a$ for$k = 8/1$ and$k = 1/8$ 
图 19 在
$k = 8/1$ 时，$n$ 值变化对导电圆柱压头接触应力$p\left( x \right)$ 和电荷分布$q\left( x \right)$ 的影响Figure 19. Effects of gradient index
$n$ on distribution of contact stress$p\left( x \right)$ and electric charge$q\left( x \right)$ for$k = 8/1$ 
图 20 在
$k = 1/8$ 时，$n$ 值变化对导电圆柱压头接触应力$p\left( x \right)$ 和电荷分布$q\left( x \right)$ 的影响Figure 20. Effects of gradient index
$n$ on distribution of contact stress$p\left( x \right)$ and electric charge$q\left( x \right)$ for$k = 1/8$ 
图 21 当
$k = 8/1$ 时，$n$ 值变化对压力与压痕曲线、压力与电势曲线、电荷与位移曲线和电荷与电势曲线的影响Figure 21. Effects of
$n$ on the curve of applied force vs. indentation, the curve of applied force vs. electrical potential, the curve of electric charge vs. indentation and the curve of electrical charge vs. electrical potential for$k = 8/1$ 
图 22 当
$k = 1/8$ 时，$n$ 值变化压力与压痕曲线、压力与电势曲线、电荷与位移曲线和电荷与电势曲线的影响Figure 22. Effects of
$n$ on the curve of applied force vs. indentation, the curve of applied force vs. electrical potential, the curve of electric charge vs. indentation and the curve of electrical charge vs. electrical potential for$k = 1/8$ 表 1 压电陶瓷PZT-4的材料参数
Table 1. Material properties of PZT-4
$ c_{11, N + 1} $/GPa $ G_{13, N + 1} $/GPa $ c_{33, N + 1} $/GPa $ C_{44, N + 1} $/GPa $ e_{31, N + 1} $/(C/m2) $ e_{33, N + 1} $/(C/m2) $ e_{15, N + 1} $/(C/m2) $ \varepsilon_{11, N + 1} $/(C/(V·m)) $ \varepsilon_{33, N + 1} $/(C/(V·m)) 139 74.3 115 25.6 −5.2 15.1 12.7 6.461×10−9 5.62×10−9 
下载: 导出CSV
-
[1] 李青山, 刘正兴, 杨耀文. 压电材料在智能结构形状和振动控制中的应用[J]. 力学进展, 1999, 29(1): 66-76 doi: 10.6052/1000-0992-1999-1-J1998-056LI Qingshan, LIU Zhengxing, YANG Yaowen. The applications of piezoelectric materials on shape control and vibration control of smart structures[J]. Advances in Mechanics, 1999, 29(1): 66-76.(in Chinese) doi: 10.6052/1000-0992-1999-1-J1998-056 [2] MASON W P. Piezoelectricity, its history and application[J]. The Journal of the Acoustical Society of America, 1980, 70(6): 1561-1566. [3] 张涛, 孙立宁, 蔡鹤皋. 压电陶瓷基本特性研究[J]. 光学精密工程, 1998, 6(5): 26-32 doi: 10.3321/j.issn:1004-924X.1998.05.005ZHANG Tao, SUN Lining, CAI Hegao. Study on the fundament characteristics of piezoelectric element[J]. Optics and Precision Engineering, 1998, 6(5): 26-32.(in Chinese) doi: 10.3321/j.issn:1004-924X.1998.05.005 [4] 路桂华, 赵曼, 岳强. 各向异性压电介质摩擦接触界面波动特性分析[J]. 应用数学和力学, 2017, 38(4): 421-431LU Guihua, ZHAO Man, YUE Qiang. Characteristics of elastic waves through frictional contact interfaces between 2 anisotropic piezoelectric materials[J]. Applied Mathematics and Mechanics, 2017, 38(4): 421-431.(in Chinese) [5] 刘兴伟, 李星, 汪文帅. 一维六方压电准晶中正n边形孔边裂纹的反平面问题[J]. 应用数学和力学, 2020, 41(7): 713-724LIU Xingwei, LI Xing, WANG Wenshuai. The anti-plane problem of regular n-polygon holes with radial edge cracks in 1D hexagonal piezoelectric quasicrystals[J]. Applied Mathematics and Mechanics, 2020, 41(7): 713-724.(in Chinese) [6] 孙文静, 王毅泽. 压电超材料梁中弹性波带隙特性与界面传输的主动控制[J]. 应用数学和力学, 2022, 43(1): 14-25SUN Wenjing, WANG Yize. Active control on band gap properties and interface transmission of elastic waves in piezoelectric metamaterial beams[J]. Applied Mathematics and Mechanics, 2022, 43(1): 14-25.(in Chinese) [7] SOSA H A, CASTRO M A. On concentrated loads at the boundary of a piezoelectric half-plane[J]. Journal of the Mechanics and Physics of Solids, 1994, 42(7): 1105-1122. doi: 10.1016/0022-5096(94)90062-0 [8] WANG Z K, ZHENG B L. The general solution of three-dimensional problem in piezoelectric media[J]. International Journal of Solids and Structures, 1995, 32(1): 105-115. doi: 10.1016/0020-7683(94)00101-2 [9] DING H J, CHEN B, LIAN G. General solutions for coupled equations for piezoelectric media[J]. International Journal of Solids & Structures, 1996, 33(16): 2283-2298. [10] CHEN W Q, SHIOYA T, DING H J. The elasto-electric field for a rigid conical punch on a transversely isotropic piezoelectric half-space[J]. Journal of Applied Mechanics, 1999, 66(3): 764-771. doi: 10.1115/1.2791738 [11] 周坤丽, 匡震邦. 压电材料中的表面电极[J]. 上海交通大学学报, 2005, 39(2): 293-296 doi: 10.3321/j.issn:1006-2467.2005.02.029ZHOU Kunli, KUANG Zhenbang. Surface electrode problem in piezoelectric materials[J]. Journal of Shanghai Jiaotong University, 2005, 39(2): 293-296.(in Chinese) doi: 10.3321/j.issn:1006-2467.2005.02.029 [12] LIU T J, WANG Y S. Axisymmetric frictionless contact problem of a functionally graded coating with exponentially varying modulus[J]. Acta Mechanica, 2008, 199: 151-165. doi: 10.1007/s00707-007-0556-3 [13] WU C C M, KAHN M, MOY W. Piezoelectric ceramics with functional gradients: a new application in material design[J]. Journal of the American Ceramic Society, 1996, 79(3): 809-812. [14] ZHU X H, MENG Z. Operational principle, fabrication and displacement characteristics of a functionally gradient piezoelectric ceramic actuator[J]. Sensors and Actuators A: Physical, 1995, 48(3): 169-176. doi: 10.1016/0924-4247(95)00996-5 [15] KE L L, YANG J, KITIPORNCHAI S, et al. Frictionless contact analysis of a functionally graded piezoelectric layered half-plane[J]. Smart Materials and Structures, 2008, 17(2): 025003. doi: 10.1088/0964-1726/17/2/025003 [16] KE L L, YANG J, KITIPORNCHAI S, et al. Electro-mechanical frictionless contact behavior of a functionally graded piezoelectric layered half-plane under a rigid punch[J]. International Journal of Solids and Structures, 2008, 45(11/12): 3313-3333. [17] LIU T J, ZHANG C Z, WANG Y S. Analysis of axisymmetric indentation of functionally graded piezoelectric coating or substrate systems under an insulator indenter[J]. Journal of Intelligent Material Systems and Structures, 2017, 28(1): 23-34. doi: 10.1177/1045389X16642305 [18] LIU T J, ZHANG C Z. Axisymmetric conducting indenter on a functionally graded piezoelectric coating[J]. International Journal of Mechanical Sciences, 2016, 115/116: 34-44. doi: 10.1016/j.ijmecsci.2016.06.008 [19] LIU T J, LI P X, ZHANG C Z. On contact problem with finite friction for a graded piezoelectric coating under an insulating spherical indenter[J]. International Journal of Engineering Science, 2017, 121: 1-13. doi: 10.1016/j.ijengsci.2017.08.001 [20] SU J, KE L L, WANG Y S. Axisymmetric partial slip contact of a functionally graded piezoelectric coating under a conducting punch[J]. Journal of Intelligent Material Systems and Structures, 2017, 28(14): 1925-1940. doi: 10.1177/1045389X16682849 [21] 苏洁. 功能梯度压电材料的摩擦接触分析[D]. 博士学位论文. 北京: 北京交通大学, 2018.SU Jie. Frictional contact analysis of functionally graded piezoelectric materials[D]. PhD Thesis. Beijing: Beijing Jiaotong University, 2018. (in Chinese) [22] ERDOGAN F, GUPTA G D. On the numerical solution of singular integral equations[J]. Quarterly of Applied Mathematics, 1972, 29(4): 525-534. doi: 10.1090/qam/408277 [23] GIANNAKOPOULOS A E, SURESH S. Theory of indentation of piezoelectric materials[J]. Acta Materialia, 1999, 47(7): 2153-2164. doi: 10.1016/S1359-6454(99)00076-2 -
计量
- 文章访问数: 495
- HTML全文浏览量: 345
- PDF下载量: 59
- 被引次数: 0
渝公网安备50010802005915号