<span style="white-space: normal;">Construction of Spatiotemporal-Coupling Optimal Low-Dimensional Dynamical Systems for Compressible Navier-Stokes Equations</span>

齐进; 吴锤结

doi:10.21656/1000-0887.430220

Construction of Spatiotemporal-Coupling Optimal Low-Dimensional Dynamical Systems for Compressible Navier-Stokes Equations

doi: 10.21656/1000-0887.430220

QI Jin^1,,
WU Chuijie^2, ,

1.
Institute of Applied Physics and Computational Mathematics, Beijing 100088, P.R.China
2.
School of Aeronautics and Astronautics, Dalian University of Technology, Dalian, Liaoning 116024, P.R.China

详细信息

中图分类号: O35
计量
- 文章访问数: 801
- HTML全文浏览量: 323
- PDF下载量: 129
- 被引次数: 0
出版历程
- 收稿日期: 2022-07-01
- 修回日期: 2022-09-30
- 网络出版日期: 2022-10-20
- 刊出日期: 2022-10-31

可压缩Navier-Stokes方程的时空耦合优化低维动力系统建模方法

齐进^1
,,
吴锤结^{2
, ,}

1.
北京应用物理与计算数学研究所，北京 100088
2.
大连理工大学航空航天学院，辽宁大连 116024

摘要

摘要:
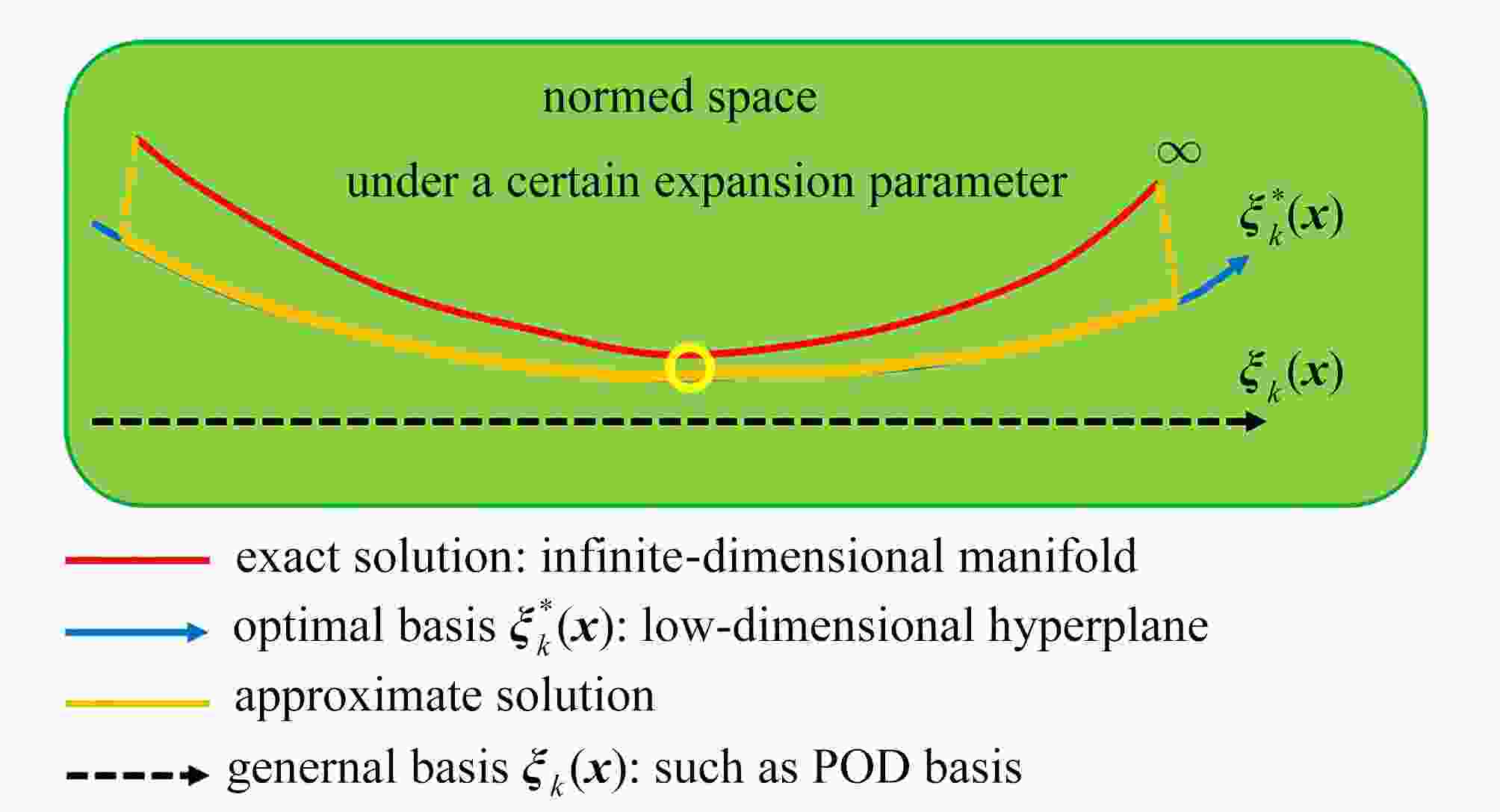
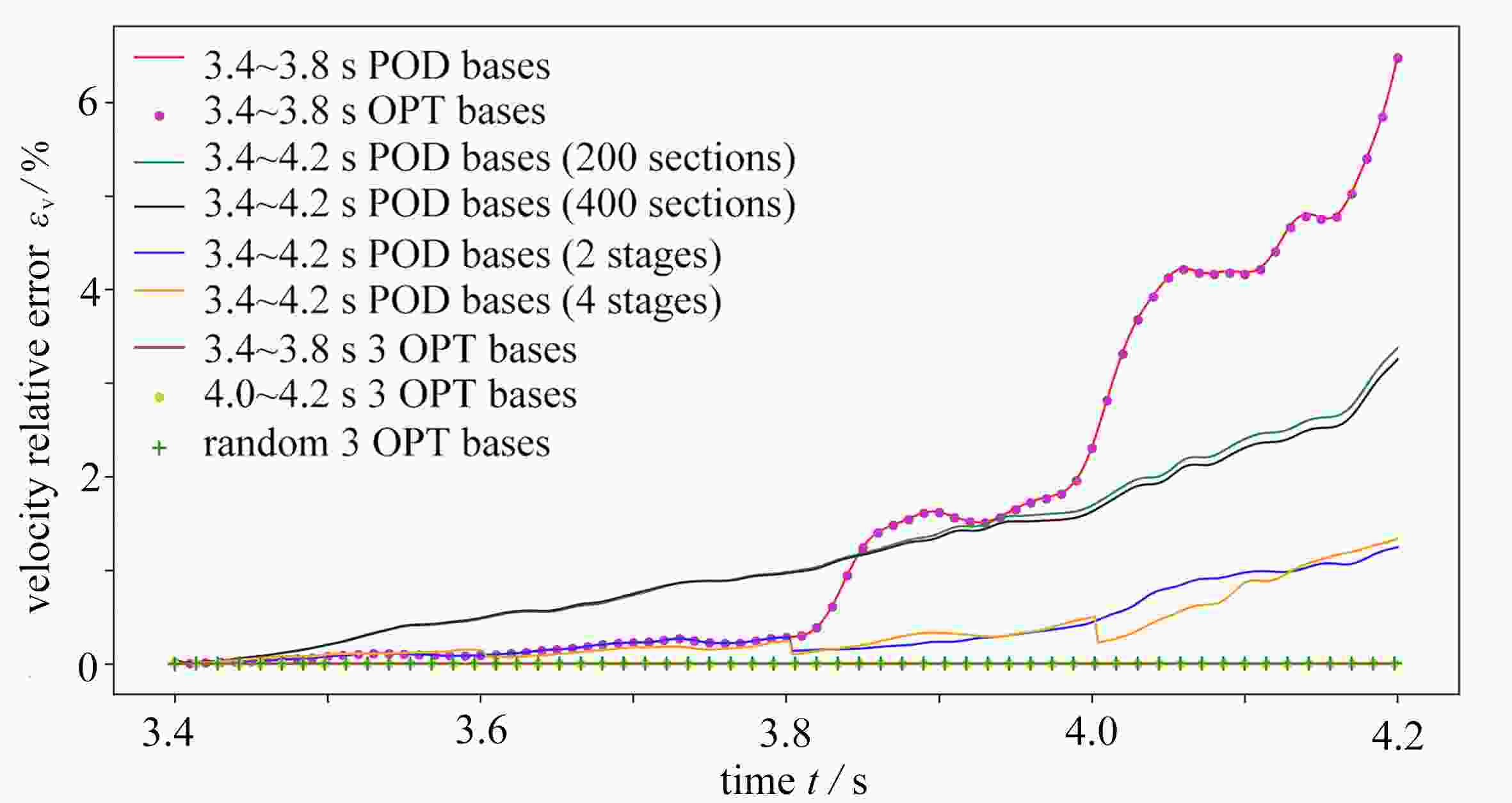
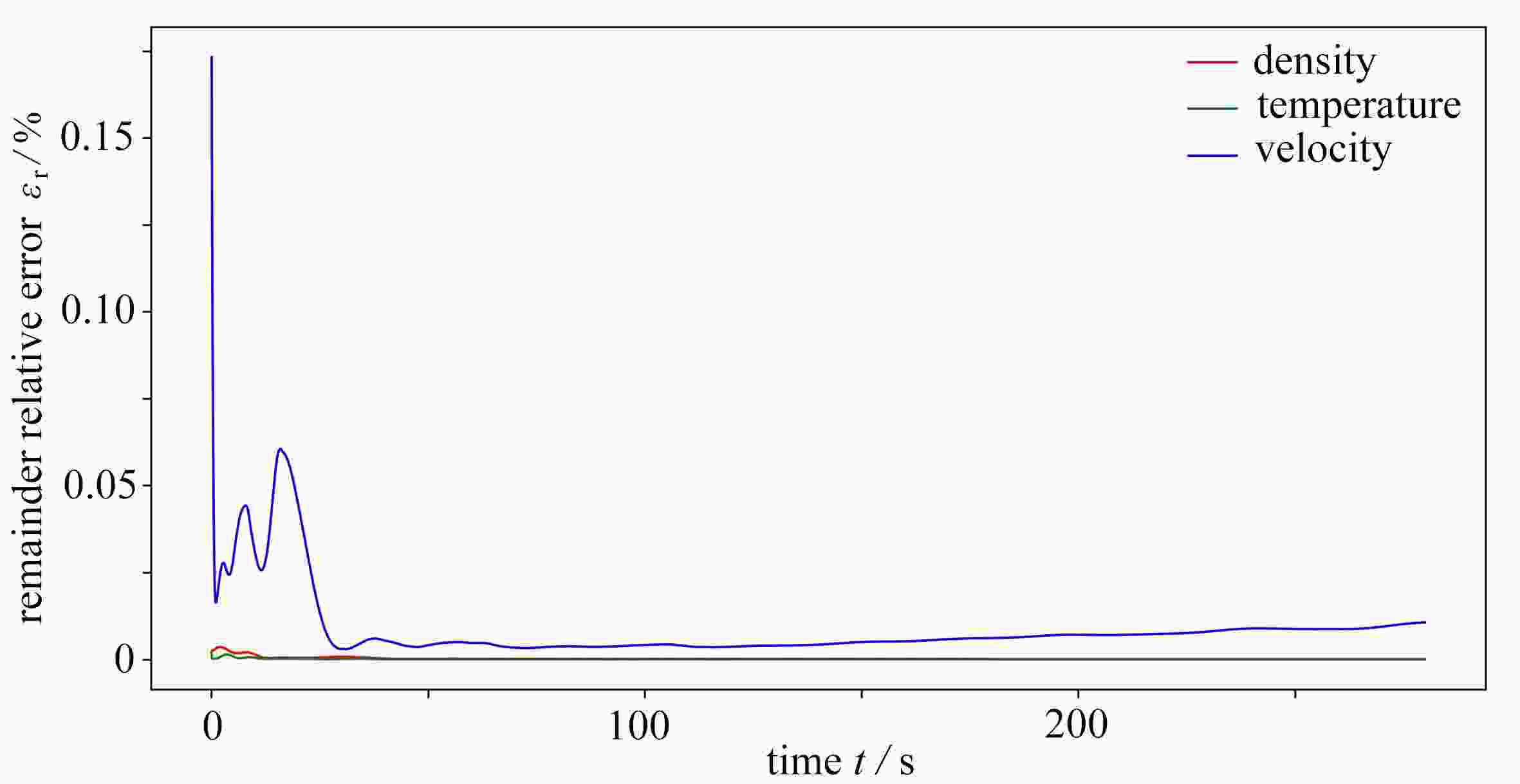
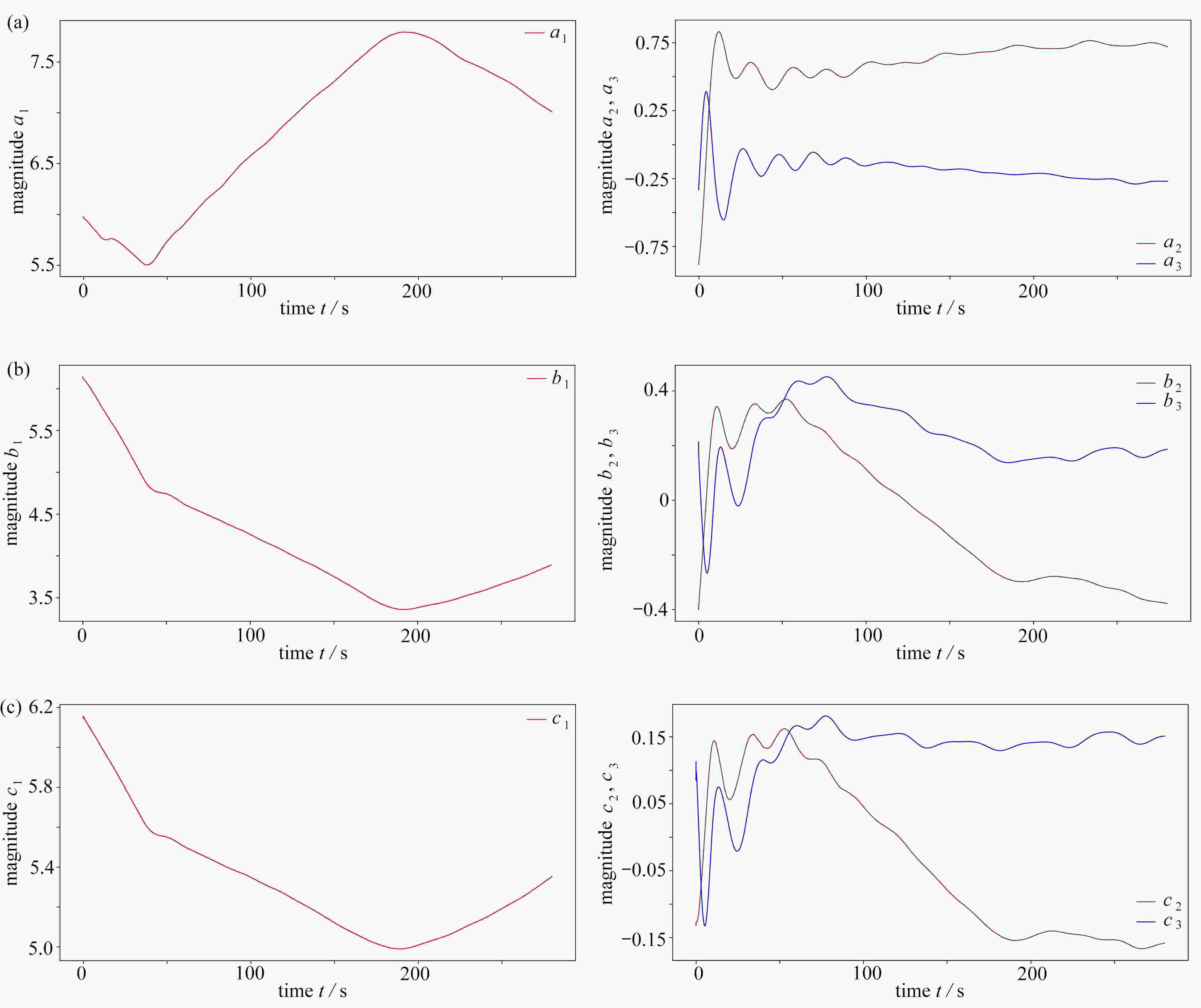
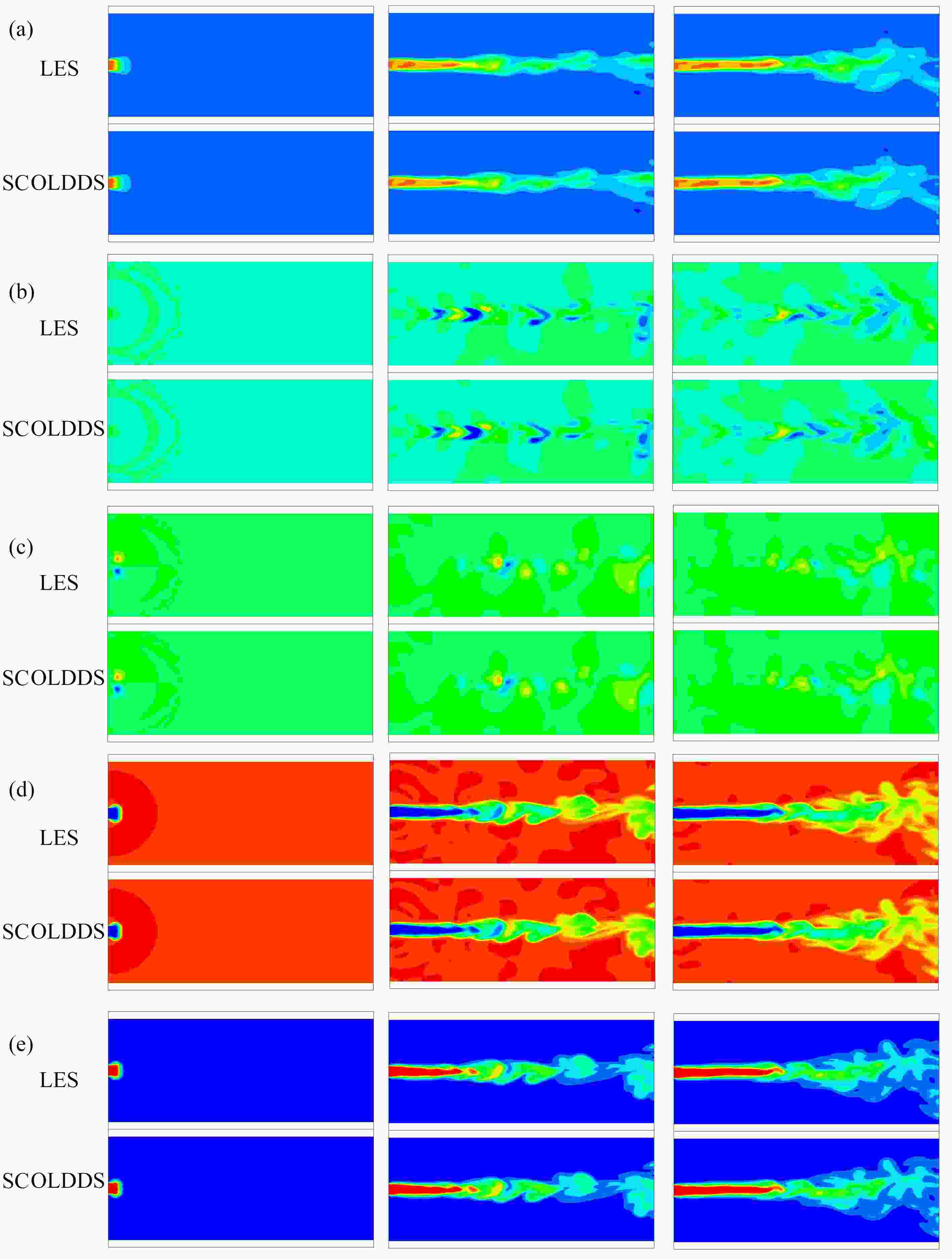
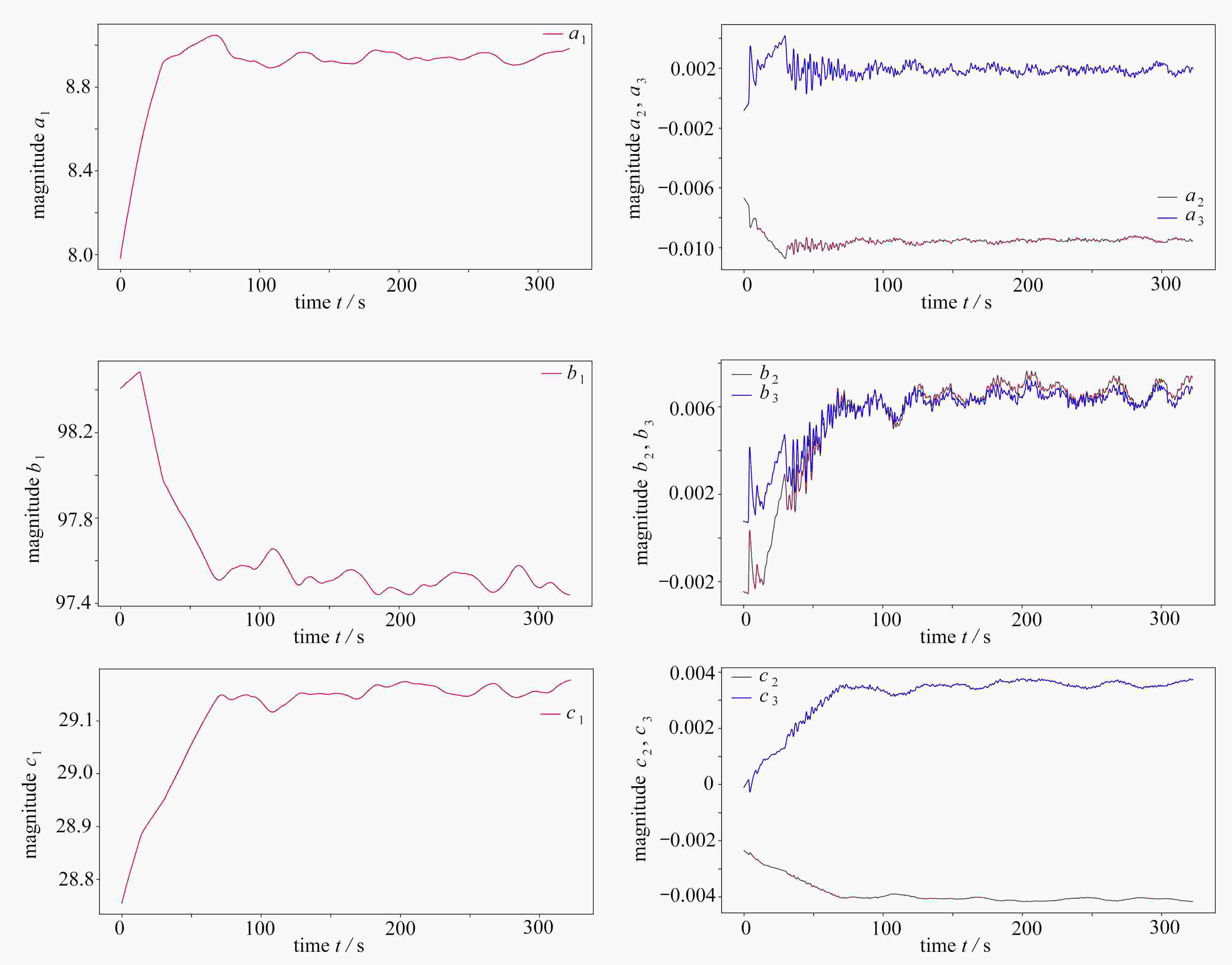
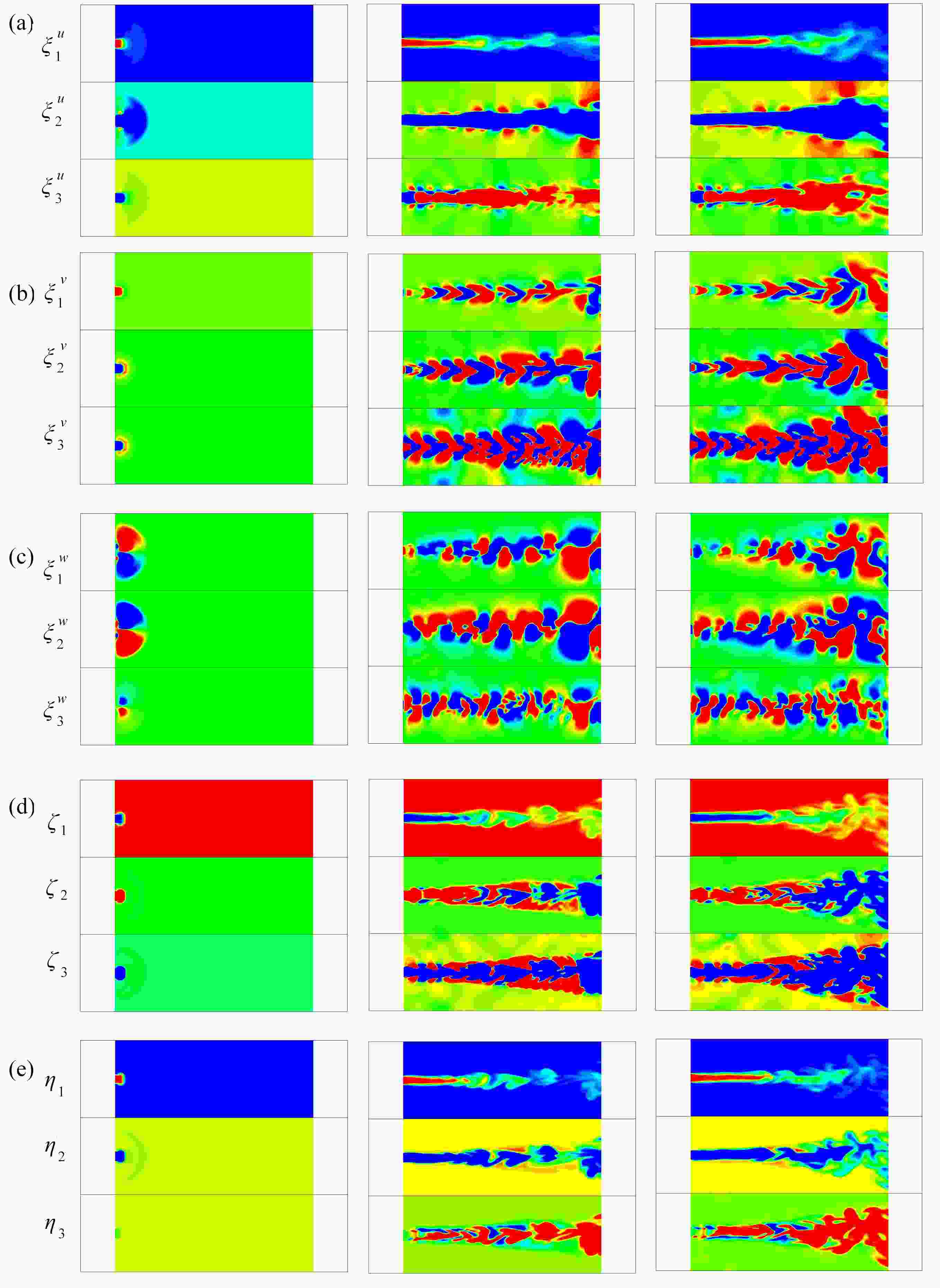
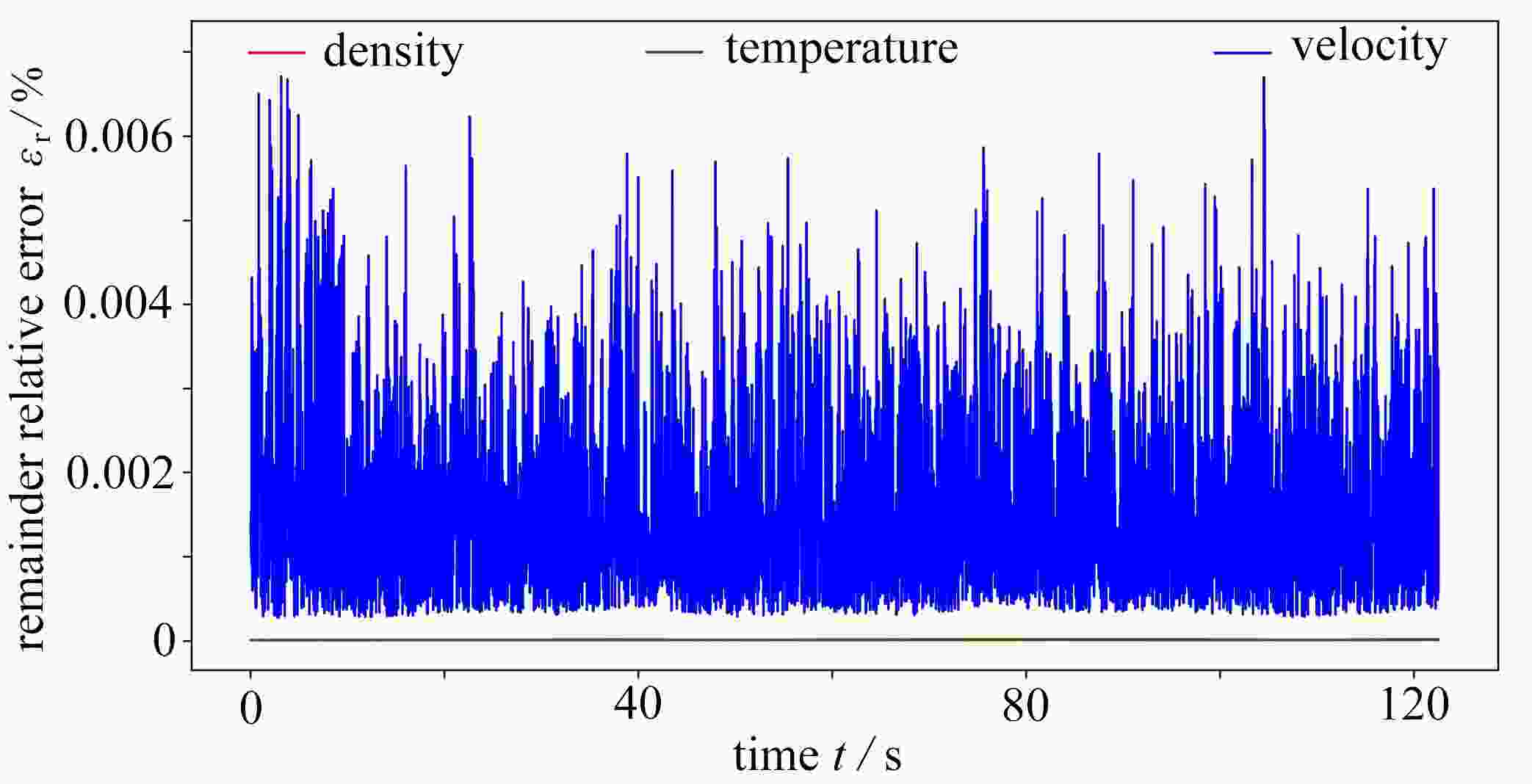
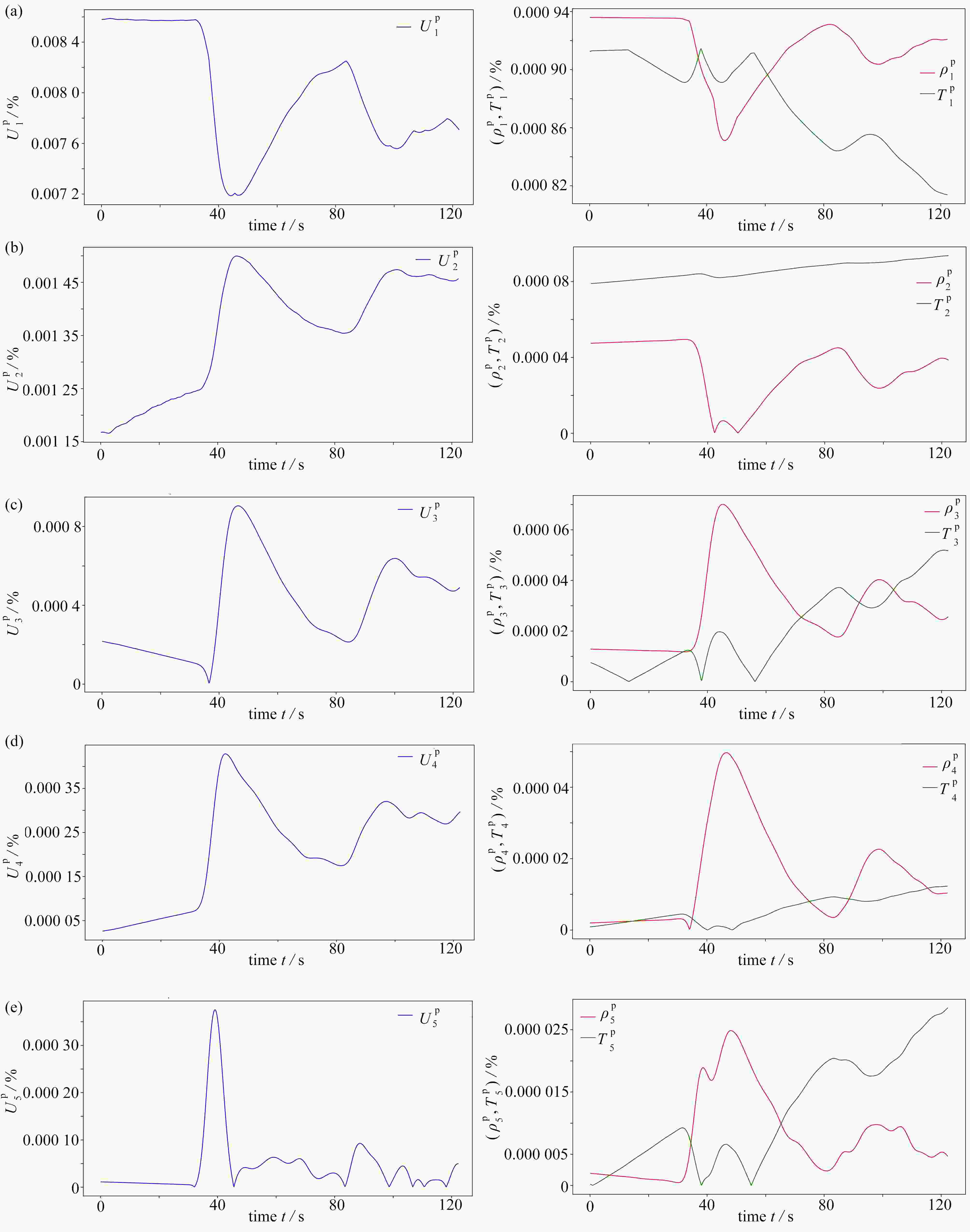
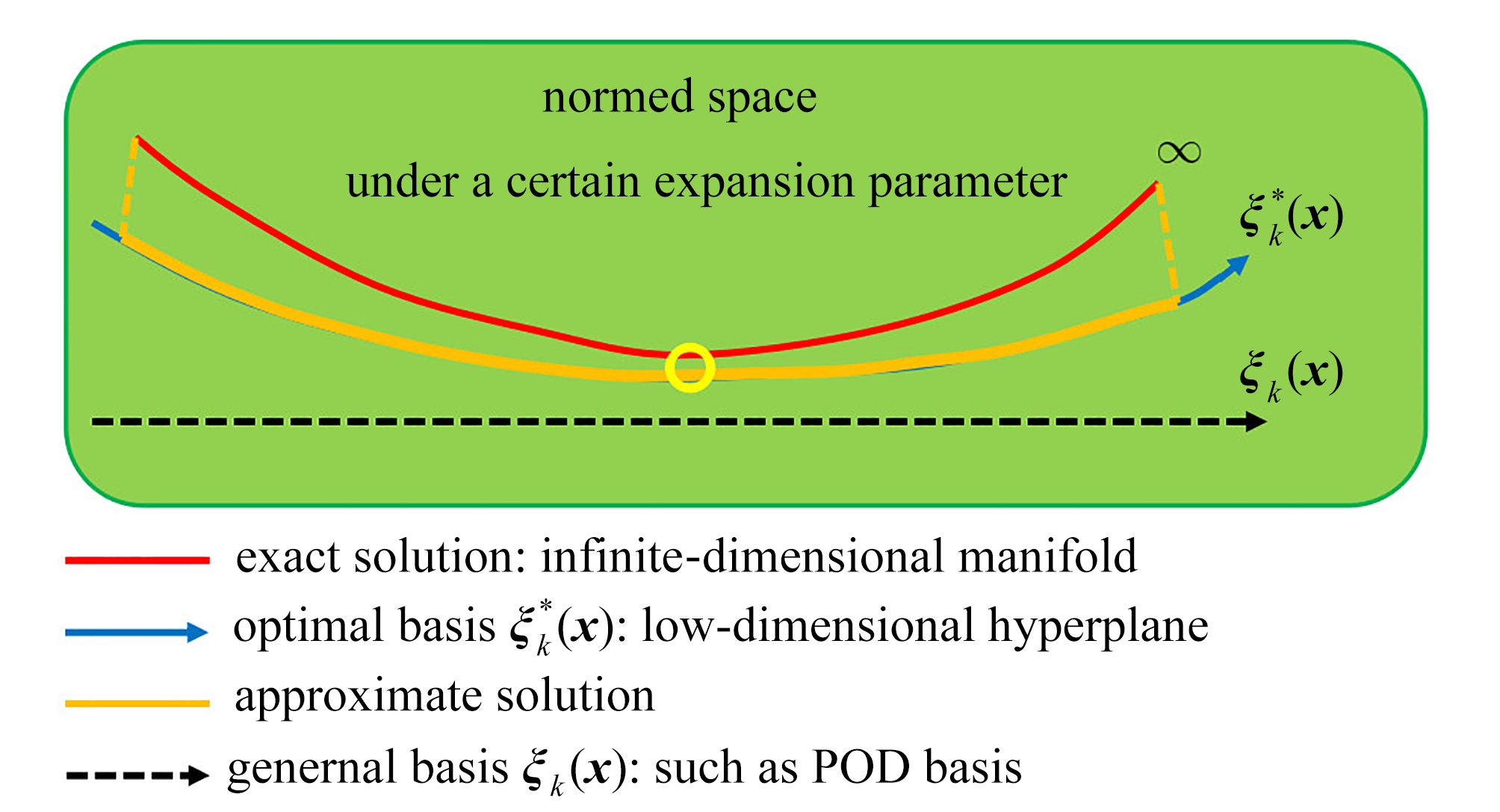
For the low-dimensional dynamical system model to study dynamics properties of Navier-Stokes equations, it is very important that the attraction domain of the low-dimensional model is the same as that of Navier-Stokes equations. However, to date, there is no universal approach to ensure this purpose for general problems. Herein, it is found that any low-dimensional model based on spatial bases, such as proper orthogonal decomposition bases, optimal spatial bases, and other classical spatial bases, is not predictable, i.e., the error increases with the time evolution of the flow field. With the theoretical framework for building optimal dynamical systems and the new concept of spatiotemporal-coupling spectrum expansion, the low-dimensional model for compressible Navier-Stokes equations was constructed to approximate the numerical solution to large-eddy simulation equations, and the numerical results and novel time evolution of spatiotemporal-coupling bases were given. The entire field error is typically below 10⁻²%, and the average error at each grid point is below 10⁻⁸%. The spatiotemporal-coupling optimal low-dimensional dynamical systems can ensure that the attraction domain of the low-dimensional model is the same as that of Navier-Stokes equations. Therefore, characteristic dynamics properties of spatiotemporal-coupling optimal low-dimensional dynamical systems are the same as those of real flow.
Abstract:
当采用低维动力系统模型研究Navier-Stokes方程的动力学性质时，保持低维模型的吸引域与Navier-Stokes方程的吸引域相同是非常重要的。然而，到目前为止，还没有一种普适的方法能确保对于一般问题都能达到这一目的。该文发现任何基于空间基的低维模型，如本征正交分解基、优化空间基和其他经典空间基，都不具有可预测性，即低维动力系统的误差随着流场的时间演化而增大。在构造优化动力系统的理论框架和时空耦合谱展开的新概念下，该文构造了可压缩Navier-Stokes方程的低维模型来逼近大涡模拟方程的数值解，给出了高精度的流场数值模拟结果和全新的时空耦合基时空演化数值结果。全场误差在10⁻²%以下，而每个网格点的平均误差在10⁻⁸%以下。时空耦合化化低维动力系统可以保证低维模型的吸引域与Navier-Stokes方程的吸引域相同。因此，保证了时空耦合优化低维动力系统的特征动力学性质与真实流场的特征动力学性质是一致的。
- 时空耦合谱展开 /
- 时空耦合优化低维动力系统 /
- 可压缩Navier-Stokes方程 /
- 大涡模拟 /
- 大涡模拟

HTML全文

Figure 1. The basic idea of the OLDDS theory

下载: 全尺寸图片幻灯片

Figure 2. Schematic diagram of the double-scale global optimization method

下载: 全尺寸图片幻灯片

Figure 3. The 3D sketch map of the compressible laminar backward-facing step flow

下载: 全尺寸图片幻灯片

Figure 4. Comparison of the evolution curves of the velocity errors with time in the whole field of low-dimensional dynamical system models constructed by POD bases, POD bases with a time interval, spatial optimal bases, SCOBs with random initial bases or POD initial bases

下载: 全尺寸图片幻灯片

Figure 5. Time evolution curves of errors of velocity, density and temperature

下载: 全尺寸图片幻灯片

Figure 6. Comparison of time evolution of flow fields of CFD and OLDDS, from left to right, $ t = 100\;{\rm{s}},300\;{\rm{s}},5\;000\;{\rm{s}},9\;990\;{\rm{s}} $: (a) velocity field u; (b) velocity field v; (c) velocity field w; (d) density field ρ; (e) temperature field T

下载: 全尺寸图片幻灯片

Figure 7. Time evolution curves of coefficients of velocity basis $ {\boldsymbol{\xi}} $, density basis $ \zeta $ and temperature basis $ \eta $

下载: 全尺寸图片幻灯片

Figure 8. Time evolution of spatiotemporal-coupling optimal velocity basis $ {{\boldsymbol{\xi}}} $, density basis $ \zeta $ and temperature basis $ \eta $: from left to right, $ t = 100\;{\rm{s}},5\;000\;{\rm{s}},9\;990\;{\rm{s}} $

下载: 全尺寸图片幻灯片

Figure 9. The 3D sketch map of the compressible turbulent straight jet flow

下载: 全尺寸图片幻灯片

Figure 10. Time evolution curves of errors of velocity, density and temperature

下载: 全尺寸图片幻灯片

Figure 11. Comparison of time evolution of turbulent flow fields between the LES and the SCOLDDS, from left to right, $ t = 100\;{\rm{s}},5\;000\;{\rm{s}},16\;670\;{\rm{s}} $: (a) velocity field u; (b) velocity field v; (c) velocity field w; (d) density field ρ; (e) temperature field T

下载: 全尺寸图片幻灯片

Figure 12. Time evolution curves of the proportion of each order of approximate flow variables: (a) the 1st-order; (b) the 2nd-order; (c) the 3rd-order

下载: 全尺寸图片幻灯片

Figure 13. Time evolution curves of coefficients of velocity basis $ {\boldsymbol{\xi}} $, density basis $ \zeta $ and temperature basis $ \eta $

下载: 全尺寸图片幻灯片

Figure 14. Time evolution of spatiotemporal-coupling optimal velocity basis $ {{\boldsymbol{\xi}}} $, density basis $ \zeta $ and temperature basis $ \eta $: from left to right, $ t = 100\;{\rm{s}},5\;000\;{\rm{s}},16\;670\;{\rm{s}} $

下载: 全尺寸图片幻灯片

Figure 15. Time evolution curves of errors of velocity, density and temperature

下载: 全尺寸图片幻灯片

Figure 16. Time evolution curves of the proportion of each order of approximate flow variables: (a) the 1st order; (b) the 2nd order; (c) the 3rd order; (d) the 4th order; (e) the 5th order

下载: 全尺寸图片幻灯片

Figure 17. Time evolution curves of coefficients of velocity basis $ {\boldsymbol{\xi}} $, density basis $ \zeta $ and temperature basis $ \eta $

下载: 全尺寸图片幻灯片

Figure 18. Time evolution of spatiotemporal-coupling optimal velocity basis $ {{\boldsymbol{\xi}}} $, density basis $ \zeta $ and temperature basis $ \eta $: from left to right, $ t = 100\;{\rm{s}},3\;000\;{\rm{s}},6\;000\;{\rm{s}} $

下载: 全尺寸图片幻灯片

参考文献(41)

[1]	POPE S B. Turbulent Flows[M]. Cambridge: Cambridge University Press, 2000.
[2]	HOFMES P, LUMLEY J L, BERKOOZ G. Turbulence, Coherent Structures, Dynamical Systems and Symmetry[M]. Cambridge: Cambridge University Press, 1996.
[3]	HOLMES P, LUMLEY J L, BERKOOZ G, et al. Turbulence, Coherent Structures, Dynamical Systems and Symmetry[M]. Cambridge: Cambridge University Press, 2012.
[4]	HALLER G. Lagrangian structures coherent[J]. Annual Review of Fluid Mechanics, 2015, 47: 137-162. doi: 10.1146/annurev-fluid-010313-141322
[5]	MENEVEAU C. Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows[J]. Annual Review of Fluid Mechanics, 2011, 43: 219-245. doi: 10.1146/annurev-fluid-122109-160708
[6]	REMPFER D. Low-dimensional modeling and numerical simulation of transition in simple shear flows[J]. Annual Review of Fluid Mechanics, 2003, 35: 229-265. doi: 10.1146/annurev.fluid.35.030602.113908
[7]	WIGGINS S. The dynamical systems approach to Lagrangian transport in oceanic flows[J]. Annual Review of Fluid Mechanics, 2005, 37: 295-328. doi: 10.1146/annurev.fluid.37.061903.175815
[8]	SHIRER H N. Nonlinear Hydrodynamic Modeling: a Mathematical Introduction[M]. Springer-Verlag, 1987.
[9]	DANIELSON T J, OTTINO J M. Structural stability in two-dimensional model flows: Lagrangian and Eulerian turbulence[J]. Physics of Fluids A, 1990, 2(11): 2024-2035. doi: 10.1063/1.857677
[10]	LUMLEY J L. The structure of inhomogeneous turbulent flows[C]//Atmospheric Turbulence and Radio Wave Propagation. Moscow: Nauka, 1967: 166-178.
[11]	POJE C, LUMLEY J L. A model for large scale structures in turbulence shear flows[J]. Journal of Fluid Mechanics, 1995, 285: 349-369. doi: 10.1017/S0022112095000577
[12]	LUMLEY J L. Coherent structures in turbulence[J]. Transition and Turbulence, 1981: 215-242.
[13]	LOÉVE M. Probability Theory[M]. Princeton: D. Van Nostrand Co Inc, 1963: 477-485.
[14]	PREISENDORFER R W. Principal Component Analysis in Meteorology and Oceanography[M]. Elservier, 1988.
[15]	BERKOOZ G, HOLMES P, LUMLEY J L. The proper orthogonal decomposition in the analysis of turbulent flows[J]. Annual Review of Fluid Mechanics, 1993, 25: 539-575. doi: 10.1146/annurev.fl.25.010193.002543
[16]	WU C J. Optimal truncated low-dimensional dynamical systems[J]. Discrete and Continuous Dynamical Systems, 1996, 2(4): 559-583. doi: 10.3934/dcds.1996.2.559
[17]	WU C J, SHI H S. An optimal theory for an expansion of flow quantities to capture the flow structures[J]. Fluid Dynamics Research, 1996, 17(2): 67-85. doi: 10.1016/0169-5983(95)00024-0
[18]	WANG L. Applications of optimization methods in fluid mechanics[D]. Master Thesis. Nanjing: PLA University of Science and Technology, 2003.
[19]	WU C J, WANG L. A method of constructing a database-free optimal dynamical system and a global optimal dynamical system[J]. Science in China, Series G: Physics, Mechanics and Astronomy, 2008, 51(7): 905-915. doi: 10.1007/s11433-008-0081-y
[20]	WU C J, ZHAO H L. Optimal low dimensional dynamical system modeling method for coherent structure of turbulence[C]//Proceedings of the Fifth National Conference on Turbulence and Flow Stability. Wuhan: Chinese Society of Mechanics, 1997.
[21]	WU C J, ZHAO H L. Generalized HWD-POD method and coupling low-dimensional dynamical systems onturbulence, dynamical systems and differential equation[J]. American Institute of Mathematical Sciences, 2001, 2001: 371-379.
[22]	WU C J, ZHAO H L. A new database-free method of constructing optimal low-dimensional dynamical systemsand its application[J]. Acta Mechanica Sinica, 2001, 33(3): 289-300.
[23]	ZHAO H L. Optimal low-dimensional dynamical systems in fluid dynamics[D]. Master Thesis. Nanjing: Air Force Institute of Meteorology, 1998.
[24]	PENG N F, GUAN H, WU C J. Research on the optimal dynamical systems of three-dimensional Navier-Stokes equations based on weighted residual[J]. Science China: Physics, Mechanics & Astronomy, 2016, 59(4): 644701.
[25]	PENG N F, GUAN H, WU C J. Optimal dynamical systems of Navier-Stokes equations based on generalized helical-wave bases and the fundamental elements of turbulence[J]. Science China: Physics, Mechanics & Astronomy, 2016, 59(11): 114713.
[26]	WANG J C, QI J, WU C J. Analysis and modelling of optimal dynamical systems of incompressible Navier-Stokes equations[J]. Applied Mathematics and Mechanics, 2020, 41(1): 1-15. doi: 10.1007/s10483-020-2560-6
[27]	WANG J C, QI J, WU C J. Modelling and dynamics analysis of optimal dynamical systems of fluctuation velocity equations for incompressible Navier-Stokes equations[J]. Applied Mathematics and Mechanics, 2020, 41(3): 235-249.
[28]	WANG J C, QI J, WU C J. Modelling and analysis of optimal dynamical systems of incompressible Navier-Stokes equations with pressure base functions[J]. Applied Mathematics and Mechanics, 2020, 41(8): 817-833.
[29]	LEONI G. A first course in Sobolev spaces[D]. Pittsburgh: Carnegie Mellon University, 2009.
[30]	ZHANG G Q, LIN Y Q. Lecture Notes of Functional Analysis[M]. Beijing: Peking University Press, 2013.
[31]	HAND L N, FINCH J D. Analytical Mechanics[M]. Cambridge: Cambridge University Press, 1998.
[32]	SAMTANEY R, PULLIN D I, KOSOVIĆ B. Direct numerical simulation of decaying compressible turbulence and shocklet statistics[J]. Physics of Fluids, 2001, 13(5): 1415-1430. doi: 10.1063/1.1355682
[33]	SHEN W D, TONG J G. Engineering Thermodynamics[M]. Beijing: Higher Education Press, 2007: 62-63.
[34]	ZHANG Y J, WANG P, HAN Z X, et al. Complete Works of Fluid Mechanics[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 1991.
[35]	SUTHERLAND W. The viscosity of gases and molecular force[J]. Philosophical Magazine, 1893, 36(223): 507-531.
[36]	FORD W. Numerical Linear Algebra With Applications[M]. London: Academic Press, 2014.
[37]	BUI T T. A parallel, finite-volume algorithm for large-eddy simulation of turbulent flows[J]. Computers & Fluids, 2000, 29(8): 877-915.
[38]	FAVRE A. Equations des gazturbulents compressible, Ⅰ: forms generals[J]. Journal de Mécanique, 1965, 4(2): 361.
[39]	FAVRE A. Equations des gazturbulents compressible, Ⅱ: méthode des vitesses moyennes, méthode des vitesses macroscopiques pondérées par la mass volumique[J]. Journal de Mécanique, 1965, 4(3): 391.
[40]	SMAGORINSKY U. General circulation experiments with the primitive equations, Ⅰ: the basic experiment[J]. Monthly Weather Review, 1963, 91(3): 99-164. doi: 10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2
[41]	YE Q K, WANG Z M. Numerical Methods in Optimization and Optimal Control[M]. Beijing: Science Press, 1986.