弹性薄壳动力学比拟的曲面论基础

薛纭; 陈立群

doi:10.21656/1000-0887.430222

弹性薄壳动力学比拟的曲面论基础

doi: 10.21656/1000-0887.430222

薛纭^1,,
陈立群^2, ,

1.
上海应用技术大学机械工程学院，上海 201418
2.
哈尔滨工业大学(深圳) 理学院力学系，广东深圳 518055

我刊编委陈立群来稿

基金项目:

国家自然科学基金项目 11872159

国家自然科学基金项目 11372195

详细信息

作者简介:
薛纭(1956—)，男，教授，博士，硕士生导师(E-mail: xy@sit.edu.cn)

通讯作者:
陈立群(1963—)，男，教授，博士，博士生导师(通讯作者. E-mail: chenliqun@hit.edu.cn)

中图分类号: O302
计量
- 文章访问数: 544
- HTML全文浏览量: 139
- PDF下载量: 126
- 被引次数: 0
出版历程
- 收稿日期: 2022-07-04
- 修回日期: 2022-08-06
- 刊出日期: 2023-05-01

A Fundamental Surface Theory for Kinetic Analogy of Thin Elastic Shells

XUE Yun^1
,,
CHEN Liqun^{2
, ,}

1.
School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 201418, P.R.China
2.
Department of Mechanics, School of Science, Harbin Institute of Technology, Shenzhen, Shenzhen, Guangdong 518055, P.R.China

Contributed by CHEN Liqun, M. AMM Editorial Board

摘要

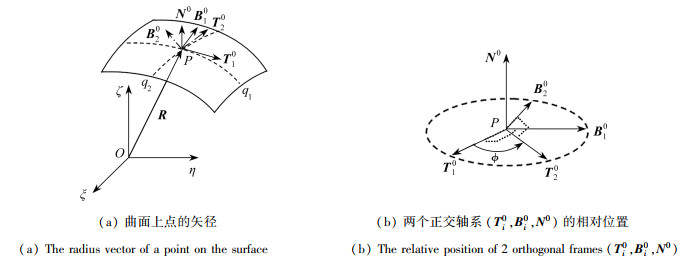
摘要: 将Kirchhoff动力学比拟从弹性细杆推广到弹性薄壳，需要相应的经典曲面论新的表达形式，即用刚体动力学的概念和方法描述曲面的基本性质，形成广义Kirchhoff动力学比拟方法. 从曲面非正交网格的两个刚性正交轴系出发，用其姿态坐标和Lamé系数表达曲面偏微分方程；用弯扭度和Lamé系数表达曲面的第一和第二基本二次型，得到了法曲率的表达式，由此计算了主曲率和主方向，验证了与经典曲面论的一致性；给出算例以说明该文方法的应用，这一方法可以用来表达曲面的Rodrigues方程、Weingarten公式和Gauss公式，以及曲面论的基本方程. 分析表明了这一方法对表述曲面微分几何的可行性，具有推导简洁和直观的优点. 这有助于为广义Kirchhoff比拟及其后续发展奠定数学基础.
- 广义Kirchhoff比拟 /
- 曲面的弯扭度 /
- 曲面第二基本二次型 /
- 弹性薄壳 /
- 刚体动力学
Abstract: The generalization of the Kirchhoff kinetic analogy from thin elastic rods to thin elastic shells, namely the generalized Kirchhoff kinetic analogy, needs a corresponding novel expression of the classical surface theory with its fundamental properties described by means of the concept and method of the rigid body dynamics. A rigid orthogonal-axis system and a curvature-twist vector were defined for the non-orthogonal meshing of a surface, and the Euler angles were used to express the attitude of the system and the partial differential geometric equation of the surface. The curvature-twist vector and the Lamé coefficient were applied to depict the 1st and the 2nd basic quadratic forms of the surface, obtain the normal curvature and calculate the principal curvature and the principal direction. The analysis demonstrates the consistency between the new and the classical expressions of the surface theory. The application example of the proposed method shows that, this method can reasonably express the Rodrigues equation, the Weingarten equation, the Gauss equation and the fundamental equations for the surface, and well describe the differential geometry of the surface. This method has the benefits of conciseness and directness, and lays a mathematical foundation for the generalized Kirchhoff kinetic analogy and its further developments.
- generalized Kirchhoff analogy /
- surface curvature-twist vector /
- surface 2nd fundamental quadratic /
- elastic thin shell /
- rigid body dynamics
edited-by

edited-by
注释:

1) 我刊编委陈立群来稿

HTML全文

图 1 曲面上点的矢径和正交轴系

Figure 1. The radius vector and orthogonal frames of a point on the surface

下载: 全尺寸图片幻灯片

图 2 轴系(e_i1, e_i2, e_i3)姿态的Euler角

Figure 2. Euler angles of the attitude of the frames (e_i1, e_i2, e_i3)

下载: 全尺寸图片幻灯片

图 3 球面坐标和球面上的轴系

Figure 3. Spherical coordinates and frames on the spherical surface

下载: 全尺寸图片幻灯片

参考文献(20)

[1]	徐晓建, 邓子辰. 基于简化的应变梯度理论下Kirchhoff板模型边值问题的提法及其应用[J]. 应用数学和力学, 2022, 43(4): 363-373. doi: 10.21656/1000-0887.420286 XU Xiaojian, DENG Zichen. Boundary value problems of a Kirchhoff type plate model based on the simplified strain gradient elasticity and the application[J]. Applied Mathematics and Mechanics, 2022, 43(4): 363-373. (in Chinese) doi: 10.21656/1000-0887.420286
[2]	王奇, 朱寅鑫, 牛培行, 等. 柔性扑翼翼型的气动性能仿真分析[J]. 应用数学和力学, 2022, 43(5): 586-596. doi: 10.21656/1000-0887.430155 WANG Qi, ZHU Yinxin, NIU Peixing, et al. Simulation of aerodynamic performances of flexible flapping wing airfoils[J]. Applied Mathematics and Mechanics, 2022, 43(5): 586-596. (in Chinese) doi: 10.21656/1000-0887.430155
[3]	LOVE A E H. A Treatise on the Mathematical Theory of Elasticity[M]. 4th ed. Dover, New York, 1927.
[4]	刘延柱. 弹性细杆的非线性力学: DNA力学模型的理论基础[M]. 北京: 清华大学出版社, 2006. LIU Yanzhu. Nonlinear Mechanics of Thin Elastic Rod: Theoretical Basis of Mechanical Model of DNA[M]. Beijing: Tsinghua University Press, 2006. (in Chinese)
[5]	COLEMAN B, SWIGON D. Theory of self-contact in Kirchhoff rods with applications to supercoiling of knotted and unknotted DNA plasmids[J]. Philosophical Transactions: Mathematical, Physical and Engineering Sciences, 2004, 362(1820): 1281-1299. doi: 10.1098/rsta.2004.1393
[6]	薛纭, 刘延柱, 陈立群. 超细长弹性杆的分析力学问题[J]. 力学学报, 2005, 37(4): 485-493. doi: 10.3321/j.issn:0459-1879.2005.04.014 XUE Yun, LIU Yanzhu, CHEN Liqun. On analytical mechanics for a super-thin elastic rod[J]. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(4): 485-493. (in Chinese) doi: 10.3321/j.issn:0459-1879.2005.04.014
[7]	XUE Yun, SHANG Huilin. Jourdain principle of a super-thin elastic rod dynamics[J]. Chinese Physics Letters, 2009, 26(7): 074501. doi: 10.1088/0256-307X/26/7/074501
[8]	薛纭, 曲佳乐, 陈立群. Cosserat生长弹性杆动力学的Gauss最小拘束原理[J]. 应用数学和力学, 2015, 36(7): 700-709. doi: 10.3879/j.issn.1000-0887.2015.07.003 XUE Yun, QU Jiale, CHEN Liqun. Gauss principle of least constraint for Cosserat growing elastic rod dynamics[J]. Applied Mathematics and Mechanics, 2015, 36(7): 700-709. (in Chinese) doi: 10.3879/j.issn.1000-0887.2015.07.003
[9]	WANG P, XUE Y, LIU Y L. Noether symmetry and conserved quantities of analytical dynamics of a Cosserat thin elastic rod[J]. Chinese Physics B, 2013, 22(10): 104503-6. doi: 10.1088/1674-1056/22/10/104503
[10]	薛纭, 陈立群, 刘延柱. Kirchhoff方程的相对常值特解及其Lyapunov稳定性[J]. 物理学报, 2004, 53(12): 4029-4036. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB200412002.htm XUE Yun, CHEN Liqun, LIU Yanzhu. Special solutions of Kirchhoff equations and their Lyapunov stability[J]. Acta Physica Sinica, 2004, 53(12): 4029-4036. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB200412002.htm
[11]	刘延柱, 薛纭. 基于精确Cosserat模型的螺旋杆稳定性分析[J]. 应用数学和力学, 2011, 32(5): 570-578. doi: 10.3879/j.issn.1000-0887.2011.05.007 LIU Yanzhu, XUE Yun. Stability analysis of a helical rod based on exact Cosserat's model[J]. Applied Mathematics and Mechanics, 2011, 32(5): 570-578. (in Chinese) doi: 10.3879/j.issn.1000-0887.2011.05.007
[12]	LEUNG A Y T, KUANG J L, LIM C W, et al. Spatial chaos of buckled elastica by the Kirchhoff analogy of a gyrostat[J]. Computers & Structures, 2005, 83(28/30): 2395-2413. http://www.onacademic.com/detail/journal_1000034066282310_ea1d.html
[13]	陈至达. 杆、板、壳大变形理论[M]. 北京: 科学出版社, 1994: 106. CHEN Zhida. Rod, Plate, Shell Large Deformation Theory[M]. Beijing: Science Press, 1994: 106. (in Chinese)
[14]	薛纭, 陈立群. Kirchhoff动力学比拟对弹性薄壳的推广[J]. 力学学报, 2021, 53(1): 234-247. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202101019.htm XUE Yun, CHEN Liqun. Generalization of Kirchhoff kinetic analogy to thin elastic shells[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(1): 234-247. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202101019.htm
[15]	吴大任. 微分几何讲义[M]. 北京: 高等教育出版社, 1959. WU Daren. Differential Geometry Lecture Notes[M]. Beijing: Higher Education Press, 1959. (in Chinese)
[16]	CAO D Q, TUCKER R W. Nonlinear dynamics of elastic rods using the Cosserat theory: modelling and simulation[J]. International Journal of Solids and Structures, 2008, 45(2): 460-477. http://www.sciencedirect.com/science/article/pii/S0020768307003253/pdfft?md5=713cbb83211a366e9ce75c9145719738&pid=1-s2.0-S0020768307003253-main.pdf
[17]	刘铖, 胡海岩. 基于李群局部标架的多柔体系统动力学建模与计算[J]. 力学学报, 2021, 53(1): 213-233. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202101018.htm LIU Cheng, HU Haiyan. Dynamic modeling and computation for flexible multibody systems based on the local frame of Lie group[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(1): 213-233. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202101018.htm
[18]	刘延柱. 高等动力学[M]. 2版. 北京: 高等教育出版社, 2016. LIU Yanzhu. Advanced Dynamics[M]. 2nd ed. Beijing: Higher Education Press, 2016. (in Chinese)
[19]	王桢, 丁洁玉. 多刚体系统动力学方向矢量模型及多步块数值方法[J]. 应用数学和力学, 2020, 41(12): 1323-1335. doi: 10.21656/1000-0887.400340 WANG Zhen, DING Jieyu. A multibody system dynamics vector model and the multistep block nemerical method[J]. Applied Mathematics and Mechanics, 2020, 41(12): 1323-1335. (in Chinese) doi: 10.21656/1000-0887.400340
[20]	关玉铭, 戈新生. 基于非约束模态的中心刚体-Timoshenko梁动力学建模与分析[J]. 应用数学和力学, 2022, 43(2): 156-165. doi: 10.21656/1000-0887.420089 GUAN Yuming, GE Xinsheng. Dynamic modeling and analysis of the central rigid body-Timoshenko beam model based on unconstrained modes[J]. Applied Mathematics and Mechanics, 2022, 43(2): 156-165. (in Chinese) doi: 10.21656/1000-0887.420089