Legendre配置谱方法求解Bose-Einstein凝聚态的基态解

刘文杰; 王汉权

doi:10.21656/1000-0887.430257

Legendre配置谱方法求解Bose-Einstein凝聚态的基态解

doi: 10.21656/1000-0887.430257

刘文杰^1,,
王汉权^{1, 2, ,}

1.
云南财经大学统计与数学学院, 昆明 650221
2.
云南师范大学数学学院, 昆明 650504

基金项目:

国家自然科学基金项目 11871418

国家自然科学基金项目 11971120

云南基础研究计划重点项目 202101AS070044

云南省教育厅科研基金项目 2022Y547

详细信息

作者简介:
刘文杰(1996—)，男，硕士生(E-mail: 1455696828@qq.com)

通讯作者:
王汉权(1974—)，男，教授，博士(通讯作者. E-mail: hanquan.wang@gmail.com)

中图分类号: O242
计量
- 文章访问数: 323
- HTML全文浏览量: 126
- PDF下载量: 49
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-10
- 修回日期: 2023-05-18
- 刊出日期: 2023-06-01

The Legendre Collocation Spectral Method for the Ground State Solutions of the Bose-Einstein Condensates

LIU Wenjie^1
,,
WANG Hanquan^{1, 2
, ,}

1.
School of Mathematics and Statistics, Yunnan University of Finance and Economics, Kunming 650221, P.R.China
2.
School of Mathematics, Yunnan Normal University, Kunming 650504, P.R.China

摘要

摘要: 近年来, 有关Bose-Einstein凝聚态基态解的实验研究已经取得了一系列重要的成果. 该文在相关研究成果的基础上, 首先通过降维和无量纲化方法将Bose-Einstein凝聚态基态解问题转换成能量泛函极值问题, 在离散该泛函时, 尝试使用Legendre配置谱方法离散该能量泛函的一维和二维情形. 其次, 对该能量泛函极小值问题进行了数值模拟. 最后，通过分析实验数据结果和图像得出，针对非旋转的Bose-Einstein凝聚态的基态解问题可以使用Legendre配置谱方法来求解, 且数值结果的误差较小.
- Bose-Einstein凝聚态 /
- Legendre配置谱方法 /
- 数值计算
Abstract: In recent years, a series of important achievements have been made in the experimental study of the ground state solutions of the Bose Einstein condensates. First, the ground state solution problem of the Bose Einstein condensate was converted into the extreme value problem of energy functional with the dimensionless method. In the discretization of the energy functional, the Legendre collocation spectral method was used in the 1D and 2D cases. Second, the energy functional minimum problem was numerically simulated. The analyses of the experimental data and graphs show that, the Legendre collocation spectral method is applicable to the ground state solution of the non-rotating Bose Einstein condensate, and the errors of the numerical results are very small.
- Bose-Einstein condensate /
- Legendre collocation spectral method /
- numerical calculation

HTML全文

图 1 一维(左图)、二维(右图)情况下, 改变N的大小, 误差ε的变化情况

Figure 1. Changes of error ε with N in the 1D case (left) and the 2D case (right)

下载: 全尺寸图片幻灯片

图 2 β=5, 10, 100, 1 000时, 一维Bose-Einstein凝聚态的基态解ϕ_g(x)

Figure 2. Ground state solution ϕ_g(x) of the 1D Bose-Einstein condensates for β=5, 10, 100, 1 000

下载: 全尺寸图片幻灯片

图 3 β=5, 10, 100, 1 000时的ϕ_g(x, y)

Figure 3. The ϕ_g(x, y) graphs for β=5, 10, 100, 1 000

下载: 全尺寸图片幻灯片

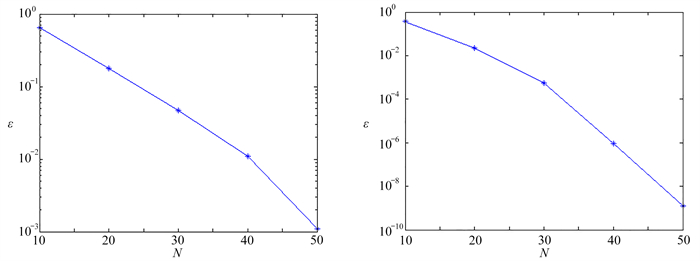
表 1 一维情况下, 改变N的大小, 误差ε的变化情况

Table 1. In the 1D case, changes of error ε with N

N	10	20	30	40	50
error ε	6.46E-1	1.79E-1	4.67E-2	1.10E-2	1.10E-3

下载: 导出CSV

表 2 二维情况下, 改变N的大小, 误差ε的变化情况

Table 2. In the 2D case, changes of error ε with N

N	10	20	30	40	50
error ε	3.65E-1	2.23E-2	5.38E-4	9.31E-7	1.22E-9

下载: 导出CSV

表 3 一维情况下Legendre配置谱方法的能量值E_β(ϕ_g)和Fourier谱方法的能量值E_β(ϕ_g^FP)与β之间的变化情况

Table 3. Energy value E_β(ϕ_g) of the Legendre collocation spectrum method and energy value E_β(ϕ_g^FP) of the Fourier spectrum method in the 1D case, changing with β

β	0	5	10	100	1 000
E_β(ϕ_g)	0.499 9	1.316 0	1.947 2	8.508 5	39.322 4
E_β(ϕ_g^FP)	0.500 0	1.316 1	1.947 1	8.508 5	39.322 4

下载: 导出CSV

表 4 二维情况下Legendre配置谱方法的能量值E_β(ϕ_g)和Fourier谱方法的能量值E_β(ϕ_g^FP)与β之间的变化情况

Table 4. Energy value E_β(ϕ_g) of the Legendre collocation spectrum method and energy value E_β(ϕ_g^FP) of the Fourier spectrum method in the 2D case, changing with β

β	0	5	10	100	1 000
E_β(ϕ_g)	1	1.437 1	1.611 7	3.983 6	12.001
E_β(ϕ_g^FP)	0.968 7	1.501 1	1.697 1	4.004 0	12.001

下载: 导出CSV

参考文献(31)

[1]	BAO W, WANG H, MARKOWICH P A. Ground, symmetric and central vortex states in rotating Bose-Einstein condensates[J]. Communications in Mathematical Sciences, 2005, 3(1): 57-88. doi: 10.4310/CMS.2005.v3.n1.a5
[2]	冯悦. Bose-Einstein凝聚基态解的时空自适应方法[D]. 硕士学位论文. 杭州: 浙江大学, 2017. FENG Yue. A spatiotemporal adaptive method for Bose-Einstein condensed ground state solutions[D]. Master Thesis. Hangzhou: Zhejiang University, 2017. (in Chinese)
[3]	LIU H, DENG D, PANG P, et al. Numerical simulations on ground states for rotating two-component Bose-Einstein condensates[J]. Advances in Applied Mathematics, 2017, 6(9): 1187-1200. doi: 10.12677/AAM.2017.69144
[4]	温建蓉, 李晋斌. 单组份玻色-爱因斯坦凝聚体基态稳定性研究[J]. 西安文理学院学报(自然科学版), 2018, 21(1): 11-15. https://www.cnki.com.cn/Article/CJFDTOTAL-XAJY201801002.htm WEN Jianrong, LI Jinbin. Research on ground state stability of single-component Bose-Einstein condensate[J]. Journal of Xi'an University(Natural Science Edition), 2018, 21(1): 11-15. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAJY201801002.htm
[5]	GAIDAMOUR J, TANG Q, ANTOINE X. BEC2HPC: a HPC spectral solver for nonlinear Schrödinger and rotating Gross-Pitaevskii equations. Stationary states computation[J]. Computer Physics Communications, 2021, 265: 108007. doi: 10.1016/j.cpc.2021.108007
[6]	王智军. 带杂质旋转玻色-爱因斯坦凝聚体基态的数值模拟[D]. 硕士学位论文. 长沙: 湖南师范大学, 2020. WANG Zhijun. Numerical simulation of the ground state of a Bose-Einstein condensate with impurities[D]. Master Thesis. Changsha: Hunan Normal University, 2020. (in Chinese)
[7]	XU F, HUANG Q, WANG M, et al. A novel adaptive finite element method for the ground state solution of Bose-Einstein condensates[J]. Applied Mathematics and Computation, 2020, 385: 125404. doi: 10.1016/j.amc.2020.125404
[8]	CHEN H, DONG G, LIU W, et al. Second-order flows for computing the ground states of rotating Bose-Einstein condensates[J]. Journal of Computational Physics, 2022, 475: 111872.
[9]	EDWARDS M, BURNETT K. Numerical solution of the nonlinear Schrödinger equation for small samples of trapped neutral atoms[J]. Physical Review A, 1995, 51(2): 1382. doi: 10.1103/PhysRevA.51.1382
[10]	BAO W, DU Q. Computing the ground state solution of Bose-Einstein condensates by a normalized gradient flow[J]. SIAM Journal on Scientific Computing, 2003, 25(5): 1674-1697.
[11]	BAO W, SHEN J. A fourth-order time-splitting Laguerre-Hermite pseudo-spectral method for Bose-Einstein condensates[J]. SIAM Journal on Scientific Computing, 2005, 26(6): 2010-2028. doi: 10.1137/030601211
[12]	BAO W, JAKSCH D, MARKOWICH P A. Numerical solution of the Gross-Pitaevskii equation for Bose-Einstein condensation[J]. Journal of Computational Physics, 2003, 187(1): 318-342. doi: 10.1016/S0021-9991(03)00102-5
[13]	舒级, 张健. 一类拟线性Schrödinger方程[J]. 应用数学和力学, 2007, 28(7): 877-882. doi: 10.3321/j.issn:1000-0887.2007.07.015 SHU Ji, ZHANG Jian. On a class of quasilinear Schrödinger equations[J]. Applied Mathematics and Mechanics, 2007, 28(7): 877-882. (in Chinese) doi: 10.3321/j.issn:1000-0887.2007.07.015
[14]	CALIARI M, RAINER S. GSGPEs: a MATLAB code for computing the ground state of systems of Gross-Pitaevskii equations[J]. Computer Physics Communications, 2013, 184(3): 812-823. doi: 10.1016/j.cpc.2012.10.007
[15]	华冬英, 邱镜亮. 玻色-爱因斯坦凝聚基态解的有限元数值计算[J]. 北京信息科技大学学报, 2011, 26(6): 21-25. doi: 10.3969/j.issn.1674-6864.2011.06.005 HUA Dongying, QIU Jingliang. Computing the ground state solution of Bose-Einstein condensations by finite element method[J]. Journal of Beijing Information Science & Technology University, 2011, 26(6): 21-25. (in Chinese) doi: 10.3969/j.issn.1674-6864.2011.06.005
[16]	WU X, WEN Z, BAO W. A regularized Newton method for computing ground states of Bose-Einstein condensates[J]. Journal of Scientific Computing, 2017, 73: 303-329. doi: 10.1007/s10915-017-0412-0
[17]	杨娜, 陈龙伟, 熊梅. 广义带导数的非线性Schrödinger方程的动态分析和精确解[J]. 应用数学和力学, 2018, 39(10): 1198-1205. doi: 10.21656/1000-0887.380302 YANG Na, CHEN Longwei, XIONG Mei. Dynamic analysis and exact solution of the general nonlinear Schrödinger equation with derivative[J]. Applied Mathematics and Mechanics, 2018, 39(10): 1198-1205. (in Chinese) doi: 10.21656/1000-0887.380302
[18]	代猛, 尹小艳. 立方Schrödinger方程的半隐格式BDF2-FEM无条件最优误差估计[J]. 应用数学和力学, 2019, 40(6): 663-681. doi: 10.21656/1000-0887.390209 DAI Meng, YIN Xiaoyan. Unconditionally optimal error estimates of the semi-implicit BDF2-FEM for cubic Schrödinger equations[J]. Applied Mathematics and Mechanics, 2019, 40(6): 663-681. (in Chinese) doi: 10.21656/1000-0887.390209
[19]	曹蕊, 华冬英, 王茜, 等. Bose-Einstein凝聚问题基态解的数值方法比较和分析[J]. 北京信息科技大学学报, 2021, 36(6): 6-13. https://www.cnki.com.cn/Article/CJFDTOTAL-BJGY202106002.htm CAO Rui, HUA Dongying, WANG Xi, et al. Comparison and analysis of numerical methods for ground state solution of Bose-Einstein condensation[J]. Journal of Beijing Information Science & Technology University, 2021, 36(6): 6-13. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJGY202106002.htm
[20]	NOCEDAL J, WRIGHT S J. Numerical Optimization[M]. 2nd ed. New York: Springer, 2006.
[21]	SHEN J, TANG T, WANG L L. Spectral Methods[M]. Berlin: Springer, 2011.
[22]	ANGLIN J R, KETTERLE W. Bose-Einstein condensation of atomic gases[J]. Nature, 2002, 436: 211-218.
[23]	DALFOVO F, GIORGINI S, PITAEVSKⅡ L P, et al. Theory of Bose-Einstein condensation in trapped gases[J]. Review of Modern Physics, 1998, 71(3): 463-512.
[24]	PETHICK C J. Bose-Einstein Condensation in Dilute Gases[M]. Cambridge: Cambridge University Press, 2008.
[25]	PITAEVSKⅡ L, STRINGARI S. Bose-Einstein condensation[J]. Physical Review Letters, 2009, 103(20): 200402. doi: 10.1103/PhysRevLett.103.200402
[26]	BAO W, TANG W. Ground state solution of Bose-Einstein condensate by directly minimizing the energy functional[J]. Journal of Computational Physics, 2003, 187(1): 230-254. doi: 10.1016/S0021-9991(03)00097-4
[27]	BAO W, CAI Y. Mathematical theory and numerical methods for Bose-Einstein condensation[J]. Kinetic and Related Models, 2013, 6(1): 1-135. doi: 10.3934/krm.2013.6.1
[28]	LIEB E H, SEIRINGER R, YNGVASON J. Bosons in a trap: a rigorous derivation of the Gross-Pitaevskii energy functional[J]. Physical Review A, 2000, 61(4): 043602. doi: 10.1103/PhysRevA.61.043602
[29]	PETHICK C J, SMITH H. Bose-Einstein Condensation in Dilute Gases: Theory of the Condensed State[M]. Cambridge: Cambridge University Press, 2001.
[30]	CANCōS E, CHAKIR R, MADAY Y. Numerical analysis of nonlinear eigenvalue problems[J]. Journal of Scientific Computing, 2009, 45(1): 1-24.
[31]	AN J, SHEN J, ZHANG Z. The spectral-Galerkin approximation of nonlinear eigenvalue problems[J]. Applied Numerical Mathematics: Transactions of IMACS, 2018, 131: 1-15.