基于同伦分析法的FGM输流管非线性频率分析

周杰; 常学平; 李映辉; 邵永波

doi:10.21656/1000-0887.430296

基于同伦分析法的FGM输流管非线性频率分析

doi: 10.21656/1000-0887.430296

1.
西南石油大学机电工程学院，成都 610500
2.
西南交通大学力学与航空航天学院，成都 610031
3.
西南石油大学土木工程与测绘学院，成都 610500

基金项目: 国家自然科学基金（51674216）

详细信息

作者简介:
周杰（1997—），男，硕士生（E-mail：17713653269@163.com）

常学平（1977—），男，副教授，博士（通讯作者. E-mail：xuepingch0952@sina.com）

中图分类号: O322
计量
- 文章访问数: 633
- HTML全文浏览量: 211
- PDF下载量: 63
- 被引次数: 0
出版历程
- 收稿日期: 2022-09-27
- 修回日期: 2023-01-05
- 网络出版日期: 2023-02-02
- 刊出日期: 2023-02-15

Nonlinear Frequency Analysis of FGM Pipes Based on the Homotopy Method

1.
School of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, P.R.China
2.
School of Mechanics and Aerospace Engineering, Southwest Jiaotong University, Chengdu 610031, P.R.China
3.
School of Civil Engineering and Geomatics, Southwest Petroleum University, Chengdu 610500, P.R.China

摘要

摘要:
该文基于同伦分析法研究了广义边界条件下含孔隙功能梯度材料(FGM)输流管道的非线性振动。基于FGM的幂律分布规律和Voigt模型来描述具有孔隙的FGM管道的材料特性。基于Euler-Bernoulli梁理论和von Kármán非线性理论，利用Hamilton变分原理，建立了含孔隙功能梯度流体输送管道的动力学控制方程和广义边界条件。采用同伦分析法求解了广义边界条件下的功能梯度流管道的非线性振动特性。数值结果表明：平移弹簧对失稳的临界流速影响不明显，而扭转弹簧则提高了失稳的临界流速，使系统更加稳定；在非线性系统中，黏弹性系数不会改变失稳临界流速；管道长度、幂律指数和孔隙率都会对FGM多孔输流管道的非线性自由振动有明显的影响。
- 同伦分析法 /
- 广义边界条件 /
- 非线性振动 /
- 孔隙率 /
- 输流管道
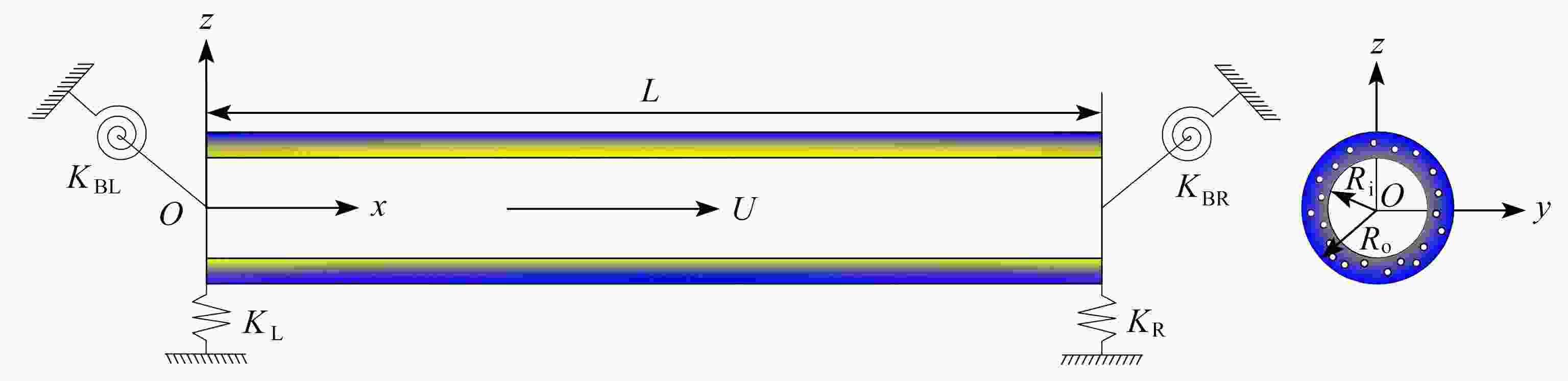
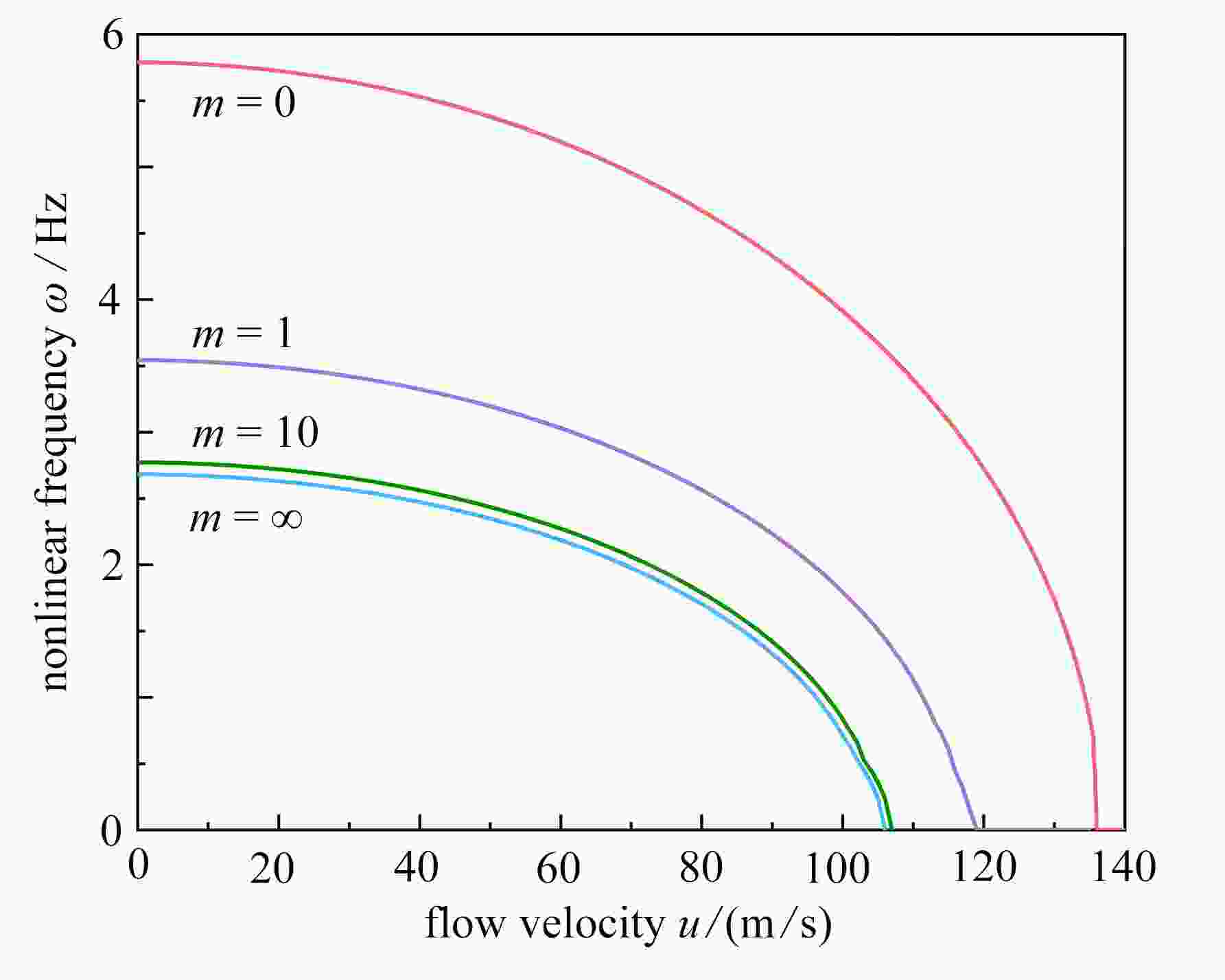
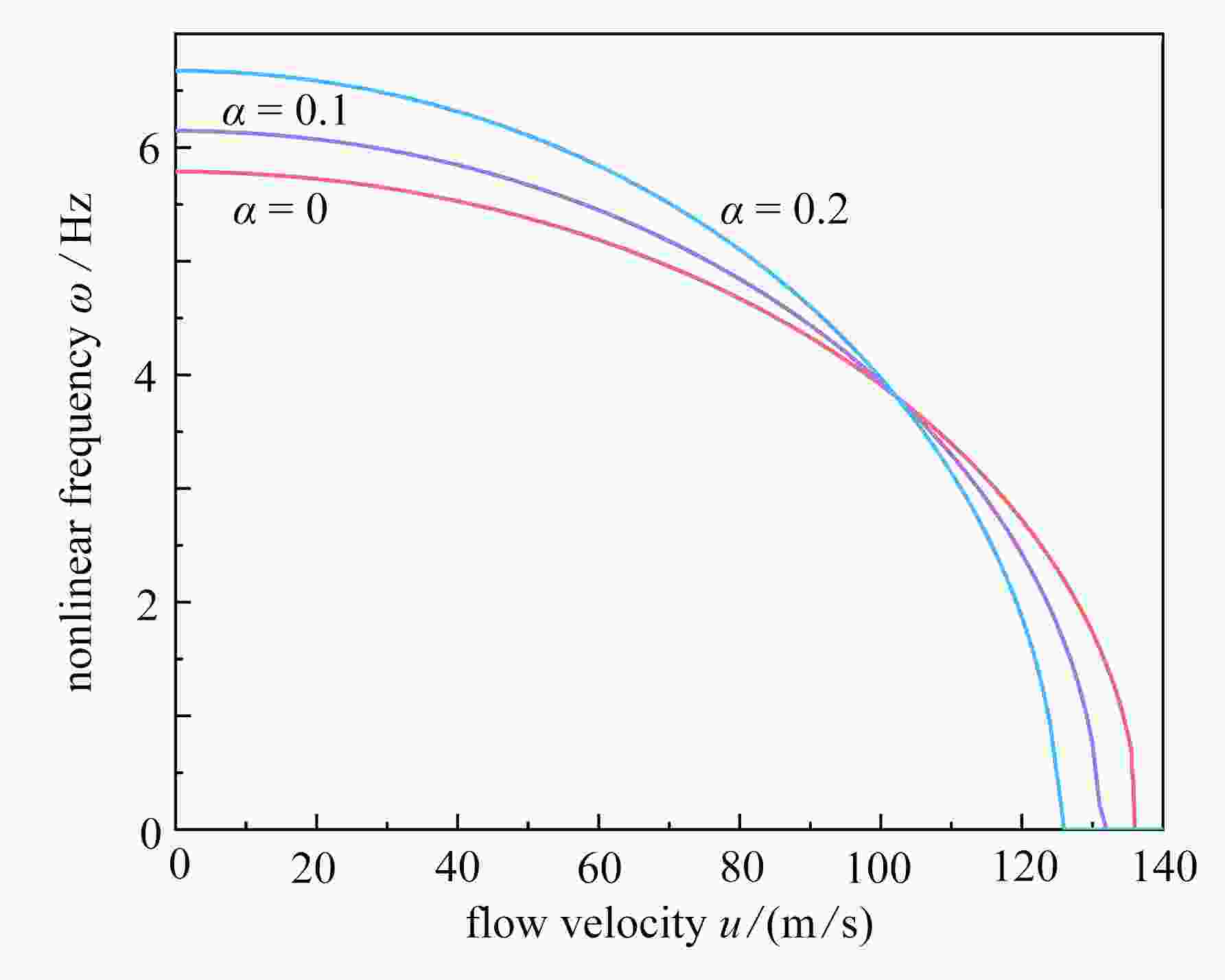
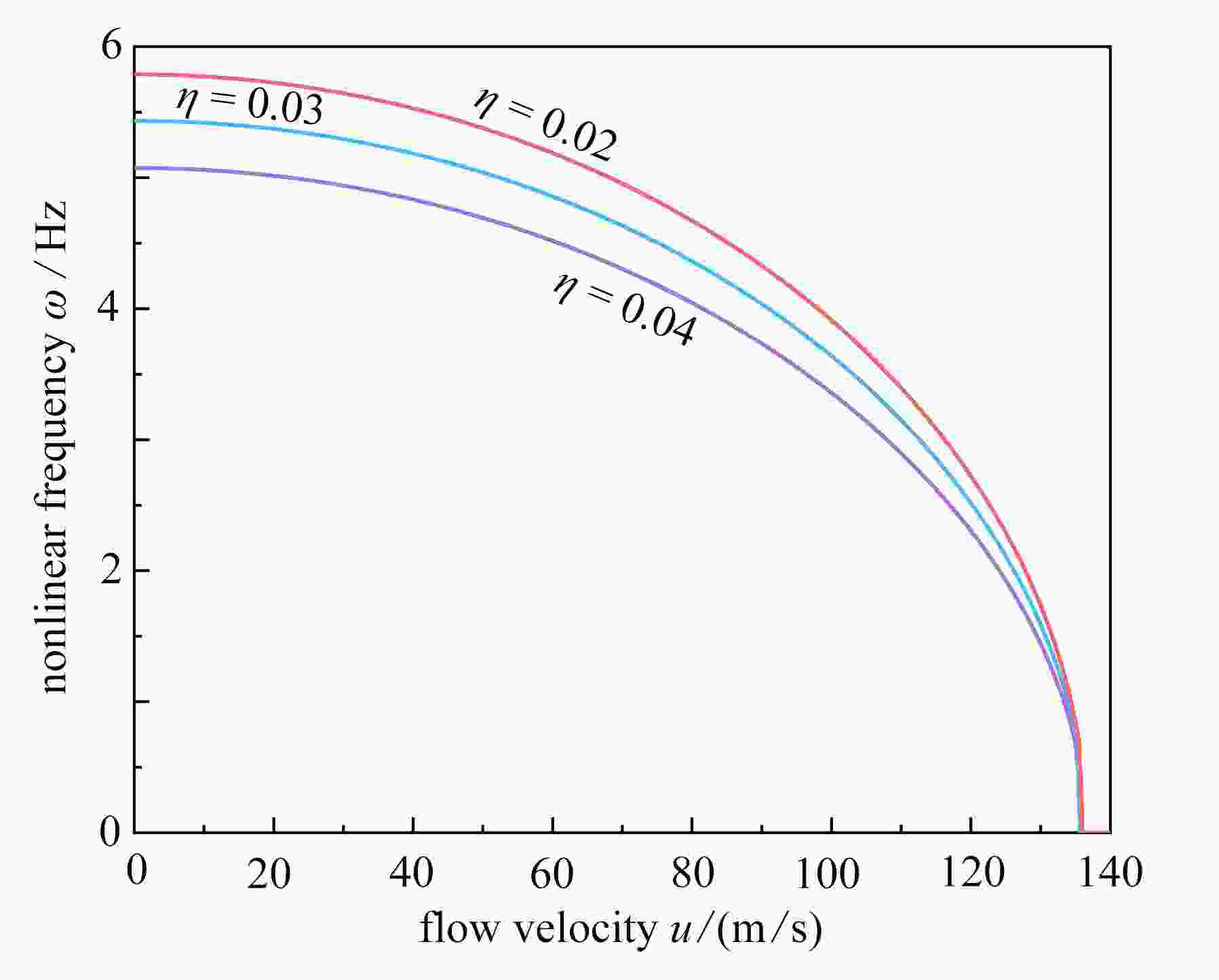
Abstract:
Based on the homotopy analysis method, the nonlinear vibration of porous functionally graded material (FGM) conveying pipes under generalized boundary conditions was studied. Based on the power-law distribution of the FGM and the Voigt model, the physical properties of the porous pipe material were described. Under the Euler-Bernoulli beam theory and the von Kármán nonlinear theory, and by means of Hamilton’s variational principle, the dynamic control equations and generalized boundary conditions for porous FGM conveying pipes were established. The homotopy analysis method was used to solve the nonlinear vibration characteristics of the porous FGM conveying pipe under generalized boundary conditions. The numerical results show that, the translation spring has little effect on the critical velocity of instability, while the rotation spring increases the critical velocity of instability, making the system more stable; in the nonlinear system, the viscoelastic coefficient does not change the critical velocity; the pipe length, the power-law exponent and the porosity all influence the nonlinear free vibration of the porous FGM conveying pipe.
- homotopy analysis /
- generalized boundary condition /
- nonlinear vibration /
- porosity /
- conveying pipe

HTML全文

图 1 广义边界条件下输送流体的管道示意图

Figure 1. Schematic diagram of a pipeline conveying fluid under generalized boundary conditions

下载: 全尺寸图片幻灯片

图 2 不同幂律指数下非线性频率随流速的变化

Figure 2. Variations of nonlinear natural frequencies with the fluid velocity under different power law indices

下载: 全尺寸图片幻灯片

图 3 不同孔隙率下非线性频率随流速的变化

Figure 3. Variations of nonlinear natural frequencies with the fluid velocity under different porosities

下载: 全尺寸图片幻灯片

图 4 不同黏弹性系数下非线性频率随流速的变化

Figure 4. Variations of nonlinear natural frequencies with the fluid velocity under different viscoelastic coefficients

下载: 全尺寸图片幻灯片

图 5 不同支撑平移弹簧刚度下非线性频率随流速的变化

Figure 5. Variations of nonlinear natural frequencies with the fluid velocity under different support spring stiffnesses

下载: 全尺寸图片幻灯片

图 6 不同扭转弹簧刚度下非线性频率随流速的变化

Figure 6. Variations of nonlinear natural frequencies with the fluid velocity under different rotating spring stiffnesses

下载: 全尺寸图片幻灯片

图 7 不同初始振幅下非线性频率随流速的变化

Figure 7. Variations of nonlinear natural frequencies with the fluid velocity under different initial amplitudes

下载: 全尺寸图片幻灯片

图 8 不同幂律指数下非线性频率随流体密度的变化

Figure 8. Variations of nonlinear natural frequencies with the fluid density under different power law indices

下载: 全尺寸图片幻灯片

图 9 不同孔隙率下非线性频率随流体密度的变化

Figure 9. Variations of nonlinear natural frequencies with the fluid density under different porosities

下载: 全尺寸图片幻灯片

参考文献(33)

[1]	TANG Y, YANG T, FANG B. Fractional dynamics of fluid-conveying pipes made of polymer-like materials[J]. Acta Mechanica Solida Sinica, 2018, 31(2): 243-258. doi: 10.1007/s10338-018-0007-9
[2]	AMIRI A, MASOUMI A, TALEBITOOTI R. Flutter and bifurcation instability analysis of fluid-conveying micro-pipes sandwiched by magnetostrictive smart layers under thermal and magnetic field[J]. International Journal of Mechanics and Materials in Design, 2020, 16: 569-588. doi: 10.1007/s10999-020-09487-w
[3]	ZHU H, WANG W, YIN X, et al. Spectral element method for vibration analysis of three-dimensional pipes conveying fluid[J]. International Journal of Mechanics and Materials in Design, 2019, 15(2): 345-360. doi: 10.1007/s10999-018-9416-7
[4]	朱晨光, 徐思朋. 功能梯度输流管的非线性自由振动分析[J]. 振动与冲击, 2018, 37(14): 195-201 ZHU Chenguang, XU Sipeng. Nonlinear free vibration analysis of FG tubes conveying fluid[J]. Journal of Vibration and Shock, 2018, 37(14): 195-201.(in Chinese)
[5]	范谨铭, 常学平, 陈美. 旋转输流管中管结构强迫振动的格林函数解[J]. 振动与冲击, 2022, 41(13): 17-25 FAN Jinming, CHANG Xueping, CHEN Mei. Green’s function solution to forced vibration of pipe-in-pine structure in rotating flow pipe[J]. Journal of Vibration and Shock, 2022, 41(13): 17-25.(in Chinese)
[6]	马腾, 杜敬涛, 许得水, 等. 任意弹性边界支承输流管路系统耦合振动特性分析[J]. 振动工程学报, 2018, 31(3): 441-449 MA Teng, DU Jingtao, XU Deshui, et al. Vibration characteristics analysis of fluid-conveying pipe system with general elastic boundary supports[J]. Journal of Vibration Engineering, 2018, 31(3): 441-449.(in Chinese)
[7]	张博, 史天姿, 张贻林, 等. 旋转输液管动力稳定性理论分析[J]. 应用数学和力学, 2022, 43(2): 166-175 ZHANG Bo, SHI Tianzi, ZHANG Yilin, et al. Theoretical analysis on dynamic stability of rotating pipes conveying fluid[J]. Applied Mathematics and Mechanics, 2022, 43(2): 166-175.(in Chinese)
[8]	龚琳琦, 陈曦昀, 郭庆, 等. 基面力单元法在空间几何非线性问题中的应用[J]. 应用数学和力学, 2021, 42(8): 785-793 GONG Linqi, CHEN Xiyun, GUO Qing, et al. Application of the base force element method to spacial geometrically nonlinear problems[J]. Applied Mathematics and Mechanics, 2021, 42(8): 785-793.(in Chinese)
[9]	包日东, 闻邦椿. 分析弹性支承输流管道的失稳临界流速[J]. 力学与实践, 2007, 29(4): 24-28 doi: 10.3969/j.issn.1000-0879.2007.04.005 BAO Ridong, WEN Bangchun. Analysis of critical instability flowrate of pipeline conveying fluid with elastic supports[J]. Mechanics in Engineering, 2007, 29(4): 24-28.(in Chinese) doi: 10.3969/j.issn.1000-0879.2007.04.005
[10]	赵千里, 孙志礼, 柴小冬. 具有弹性支承输流管路的振动分析[J]. 振动、测试与诊断, 2017, 37(6): 1222-1226 ZHAO Qianli, SUN Zhili, CHAI Xiaodong. Vibration analysis of fluid conveying pipe with elastic support[J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(6): 1222-1226.(in Chinese)
[11]	巨维博, 顾致平, 苟兵旺. 支承刚度对输流管道振动特性的影响分析[J]. 西安工业大学学报, 2011, 31(7): 616-620 JU Weibo, GU Zhiping, GOU Bingwang. Analysis of the influence of support stiffness on the vibration characteristics of flow transmission pipeline[J]. Journal of Xi’an Technological University, 2011, 31(7): 616-620.(in Chinese)
[12]	BABAEI H, ESLAMI M R. Nonlinear bending analysis of size-dependent FG porous microtubes in thermal environment based on modified couple stress theory[J]. Mechanics Based Design of Structure and Machines, 2020, 50(8): 2714-2735.
[13]	ZHU B, XU Q, LI M, et al. Nonlinear free and forced vibrations of porous functionally graded pipes conveying fluid and resting on nonlinear elastic foundation[J]. Composite Structures, 2020, 252: 112672. doi: 10.1016/j.compstruct.2020.112672
[14]	LONG V T, VAN TUNG H. Thermal nonlinear buckling of shear deformable functionally graded cylindrical shells with porosities[J]. AIAA Journal, 2021, 59(6): 2233-2241. doi: 10.2514/1.J060026
[15]	LIU Y, QIN Z, CHU F. Nonlinear forced vibrations of FGM sandwich cylindrical shells with porosities on an elastic substrate[J]. Nonlinear Dynamics, 2021, 104(2): 1007-1021. doi: 10.1007/s11071-021-06358-7
[16]	SETOODEH A R, AFRAHIM S. Nonlinear dynamic analysis of FG micro-pipes conveying fluid based on strain gradient theory[J]. Composite Structures, 2014, 116: 128-135. doi: 10.1016/j.compstruct.2014.05.013
[17]	GHAZAVI M R, MOLKI H, BEIGLOO A A. Nonlinear vibration and stability analysis of the curved microtube conveying fluid as a model of the micro coriolis flowmeters based on strain gradient theory[J]. Applied Mathematical Modelling, 2017, 45: 1020-1030. doi: 10.1016/j.apm.2017.01.048
[18]	KHODABAKHSH R, SAIDI A R, BAHAADINI R. An analytical solution for nonlinear vibration and post-buckling of functionally graded pipes conveying fluid considering the rotary inertia and shear deformation effects[J]. Applied Ocean Research, 2020, 101: 102277. doi: 10.1016/j.apor.2020.102277
[19]	MASHROUTEH S, SADRI M, YOUNESIAN D, et al. Nonlinear vibration analysis of fluid-conveying microtubes[J]. Nonlinear Dynamics, 2016, 85(2): 1007-1021. doi: 10.1007/s11071-016-2739-8
[20]	DEHROUYEH-SEMNANI A M, NIKKHAH-BAHRAMI M, YAZDI M R H. On nonlinear stability of fluid-conveying imperfect micropipes[J]. International Journal of Engineering Science, 2017, 120: 254-271. doi: 10.1016/j.ijengsci.2017.08.004
[21]	KHEIRI M. Nonlinear dynamics of imperfectly-supported pipes conveying fluid[J]. Journal of Fluids and Structures, 2020, 93: 102850. doi: 10.1016/j.jfluidstructs.2019.102850
[22]	WATSON L T. Globally convergent homotopy methods: a tutorial[J]. Applied Mathematics and Computation, 1989, 31: 369-396. doi: 10.1016/0096-3003(89)90129-X
[23]	ROITHMAYR C M, HODGES D H. Dynamics: theory and application of Kane’s method[J]. Journal of Computational and Nonlinear Dynamics, 2016, 11(6): 066501. doi: 10.1115/1.4034731
[24]	廖世俊. 关于非线性问题求解的同伦分析技术[D]. 博士学位论文. 上海: 上海交通大学, 1992. LIAO Shijun. The proposed homotopy analysis technique for the solution of nonlinear problems[D]. PhD Thesis. Shanghai: Shanghai Jiao Tong University, 1992. (in Chinese)
[25]	ALI-ASGARI M, MIRDAMADI H R, GHAYOUR M. Coupled effects of nano-size, stretching, and slip boundary conditions on nonlinear vibrations of nano-tube conveying fluid by the homotopy analysis method[J]. Physica E: Low-Dimensional of Sysems and Nanostructures, 2013, 52: 77-85. doi: 10.1016/j.physe.2013.03.031
[26]	SETOODEH A, REZAEI M, SHAHRI M R Z. Linear and nonlinear torsional free vibration of functionally graded micro/nano-tubes based on modified couple stress theory[J]. Applied Mathematics and Mechanics (English Edition), 2016, 37(6): 725-740. doi: 10.1007/s10483-016-2085-6
[27]	TANG Y, YANG T. Post-buckling behavior and nonlinear vibration analysis of a fluid-conveying pipe composed of functionally graded material[J]. Composite Structures, 2018, 185: 393-400. doi: 10.1016/j.compstruct.2017.11.032
[28]	WATTANASAKULPONG N, UNGBHAKORN V. Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities[J]. Aerospace Science and Technology, 2014, 31(1): 111-120.
[29]	EBRAHIMI F, GHASEMI F, SALARI E. Investigating thermal effects on vibration behavior of temperature-dependent compositionally graded Euler beams with porosities[J]. Meccanica, 2016, 51(1): 223-249. doi: 10.1007/s11012-015-0208-y
[30]	JIN J D, SONG Z Y. Parametric resonances of supported pipes conveying pulsating fluid[J]. Journal of Fluids and Structures, 2005, 20(6): 763-783. doi: 10.1016/j.jfluidstructs.2005.04.007
[31]	PANDA L N, KAR R C. Nonlinear dynamics of a pipe conveying pulsating fluid with parametric and internal resonances[J]. Nonlinear Dynamics, 2007, 49: 9-30. doi: 10.1007/s11071-006-9100-6
[32]	崔继峰. 应用同伦分析方法求解若干非线性周期振动问题[D]. 博士学位论文. 上海: 上海交通大学, 2015. CUI Jifeng. Applying of homotopy analysis method to some nonlinear periodic oscillation problems[D]. PhD Thesis. Shanghai: Shanghai Jiao Tong University, 2015. (in Chinese)
[33]	DENG J, LIU Y, ZHANG Z, et al. Stability analysis of multi-span viscoelastic functionally graded material pipes conveying fluid using a hybrid method[J]. European Journal of Mechanics A: Solids, 2017, 65: 257-270. doi: 10.1016/j.euromechsol.2017.04.003