Modeling of Electric Vehicles as Mobile Energy Storage Systems Considering Multiple Congestions
-
摘要:
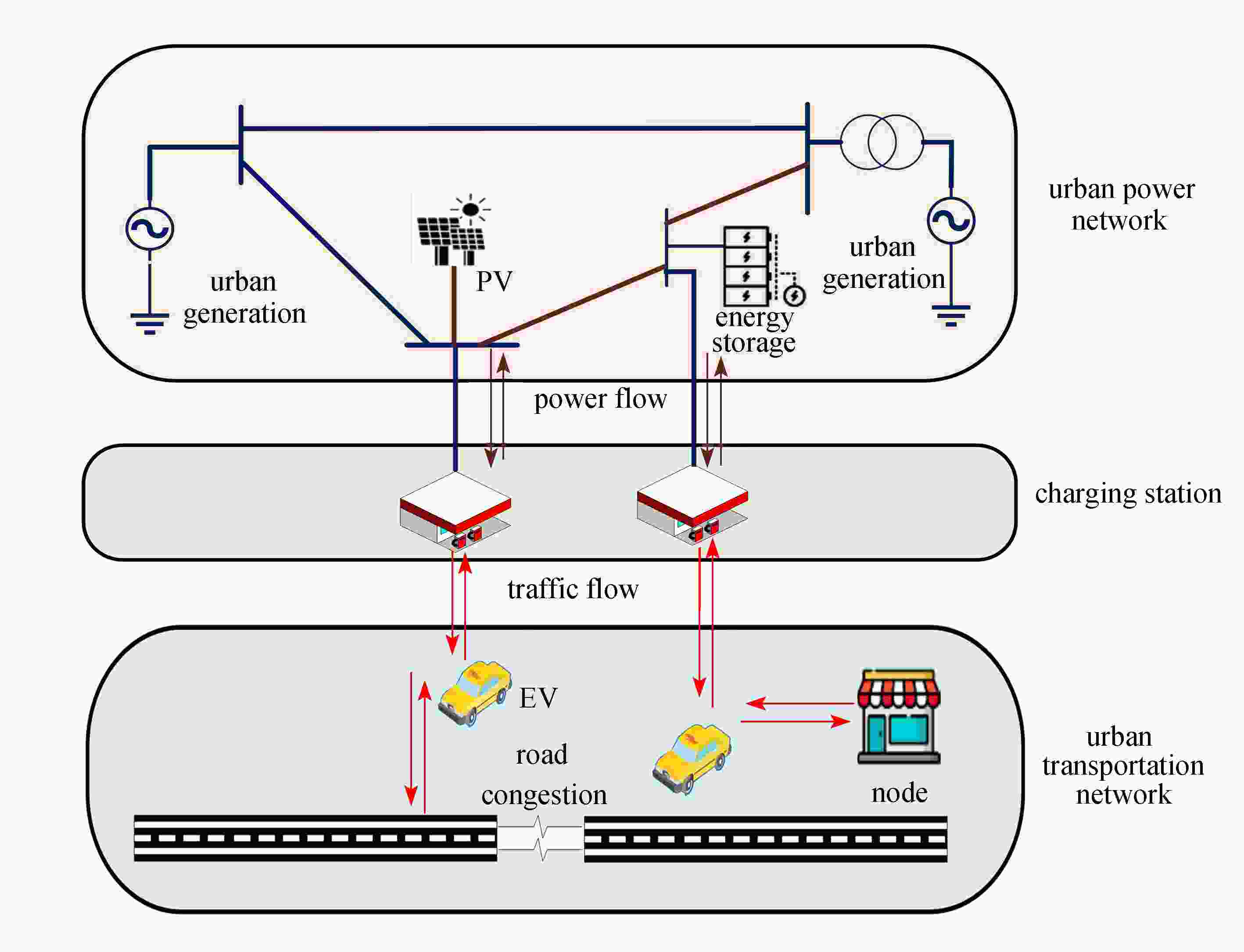
为实现城市交通电力耦合系统在城市道路、充电设施、输电线路阻塞环境下的优化运行，提出了计及多重阻塞的动态交通电力流联合优化方法。首先，基于时空网络模型，提出了计及电动汽车移动、静止、充电、排队模式的队列时空网络模型，构建了适用于电动汽车的车辆调度模型，进而形成动态交通分配模型，以减少交通出行损失。其次，通过优化发电机组、储能等的出力和备用计划，计及城市电网安全、备用约束，构建了安全约束动态经济调度模型，以降低碳排放及发电成本。随后，形成多目标动态优化模型，并将其转换为混合整数凸二次规划问题。最后，在耦合IEEE-30、Sioux Falls系统中验证了所提模型的有效性。
-
关键词:
- 阻塞 /
- 动态交通分配 /
- 队列时空网络 /
- 城市交通电力耦合系统
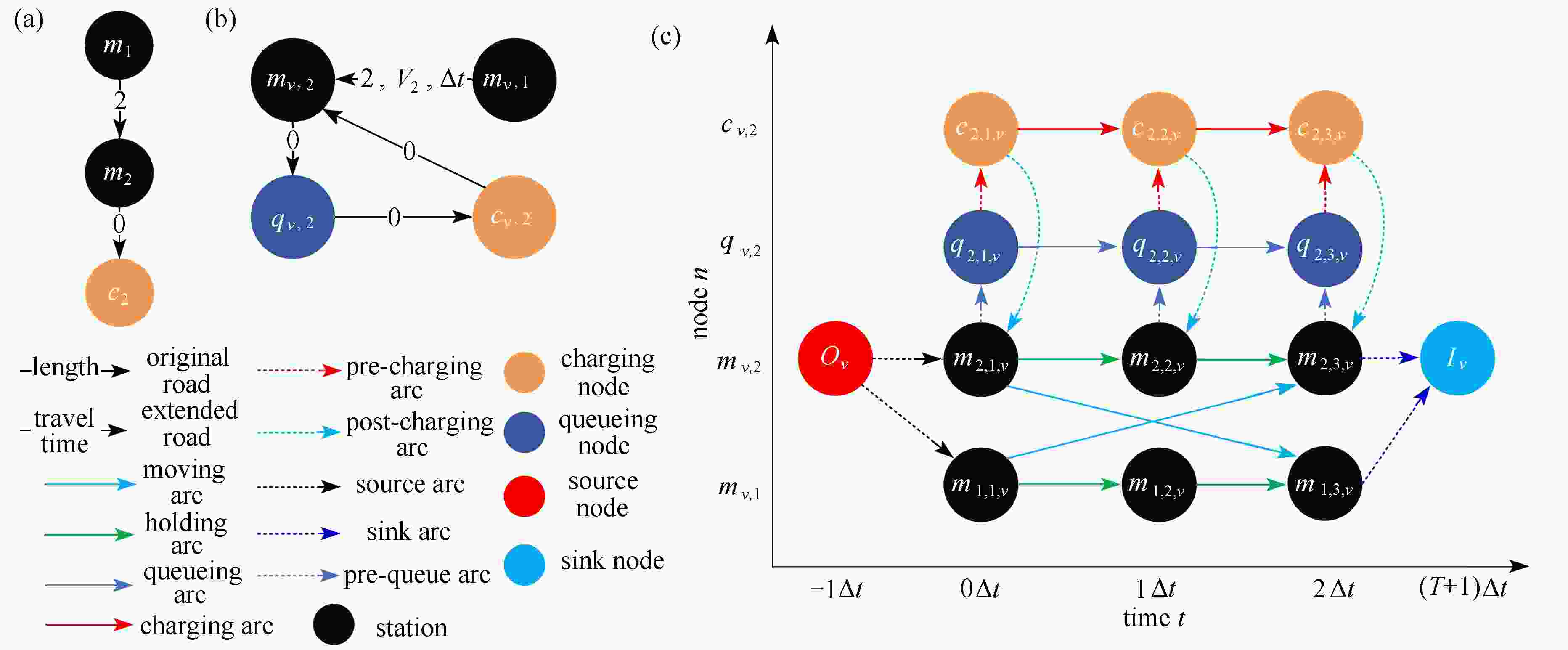
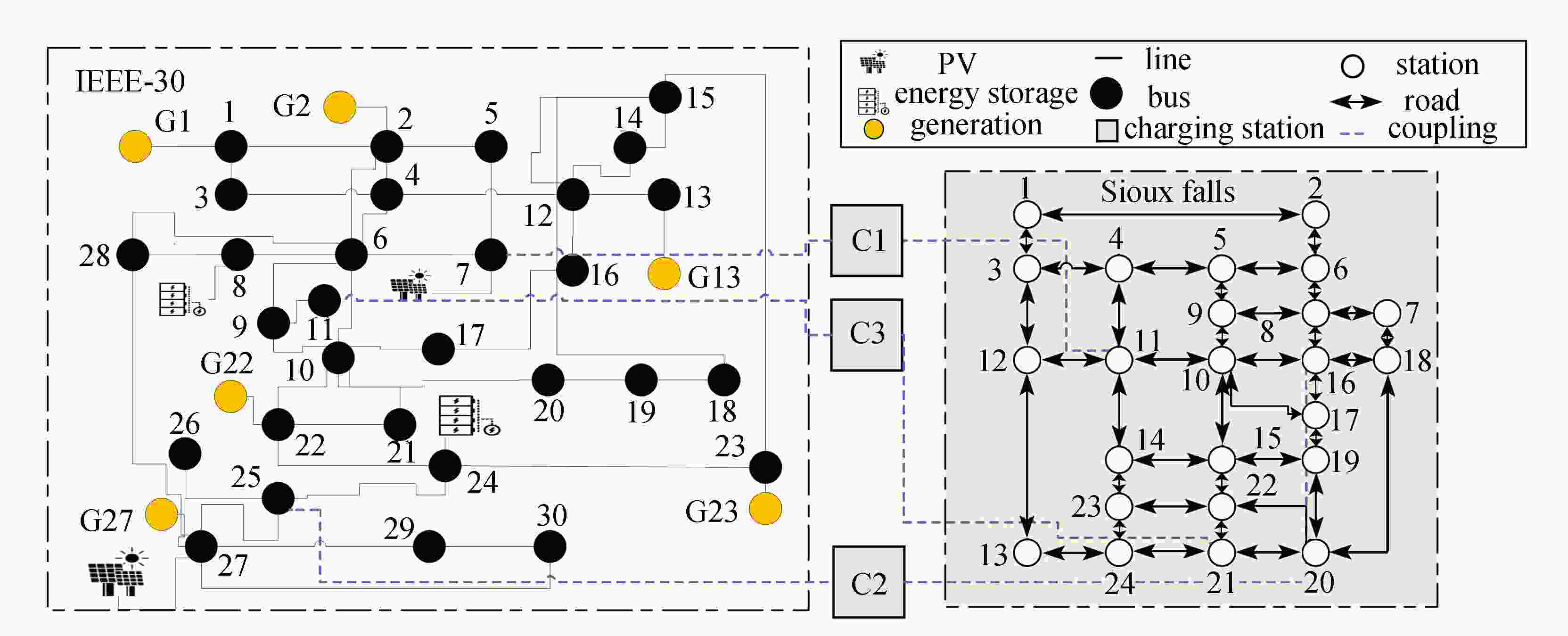
Abstract:To realize the optimal operation of urban coupled transportation power systems underthe road, charging facilities, and transmission line congestions, a dynamic optimal traffic power flow (DOTPF) model was formulated under congestions. Based on the time space network (TSN) approach, a novel TSN with queues was proposed, considering the moving, parking, charging, and queueing state transitions. A vehicle routing problem was formulated for electric vehicles (EVs) and further incorporated into the dynamic traffic assignment problem (DTAP), reducing the traffic demand losses. With security and reserve constraints, a dynamic security-constrained carbon dioxide-oriented optimal power flow (OPF) problem was formulated to reduce the carbon emission and generation cost, by optimizing the scheduling of thermal units and energy storage systems. A multi-objective DOTPF problem was formulated, and further reformulated into a convex mixed-integer quadratic programming problem. The effectiveness of the proposed DOTPF was verified based on the simulation results on coupled IEEE-30 and Sioux Falls system.
-
图 3 不同情景下总充放电负荷曲线
Figure 3. Total charging/discharging load profile under different scenarios
表 1 仿真情景设计
Table 1. Simulation scenarios
scenario road congestion charging congestion line congestion 1 − − − 2 capacities of roads (1, 2) and (1, 4) are reduced to 25% during 2:00—16:00 − − 3 − capacities of charging stations are 1 fleet during 0:00—24:00 − 4 − − capacities of lines (2, 4) and (3, 4) are reduced to 20% during 7:00—15:00 5 capacities of roads (1, 2) and (1, 4) are reduced to 25% during 2:00—16:00 capacities of charging stations are 1 fleet during 0:00—24:00 − 6 capacity of roads (1, 2) and (1, 4) are reduced to 25% during 2:00—16:00 capacities of charging stations are 1 fleet during 0:00—24:00 capacities of lines (2, 4) and (3, 4) are reduced to 20% during 7:00—15:00 
下载: 导出CSV
表 2 测试系统1各情景下计算结果
Table 2. Results under different scenarios for case 1
scenario total cost Ctotal/$ generation cost Cgeneration/$ carbon emission Mcarbon/t unmet traffic demand D 1 104 356.54 68 517.91 1 396.38 4 900 2 108 356.48 68 517.71 1 396.40 5 700 3 112 091.69 67 626.85 1 473.50 6 500 4 115 984.50 68 140.42 1 397.05 7 300 5 112 092.09 67 628.23 1 473.38 6 500 6 120 024.68 67 663.61 1 460.72 8 100
下载: 导出CSV
表 3 测试系统2各情景下计算结果
Table 3. Results under different scenarios for case 2
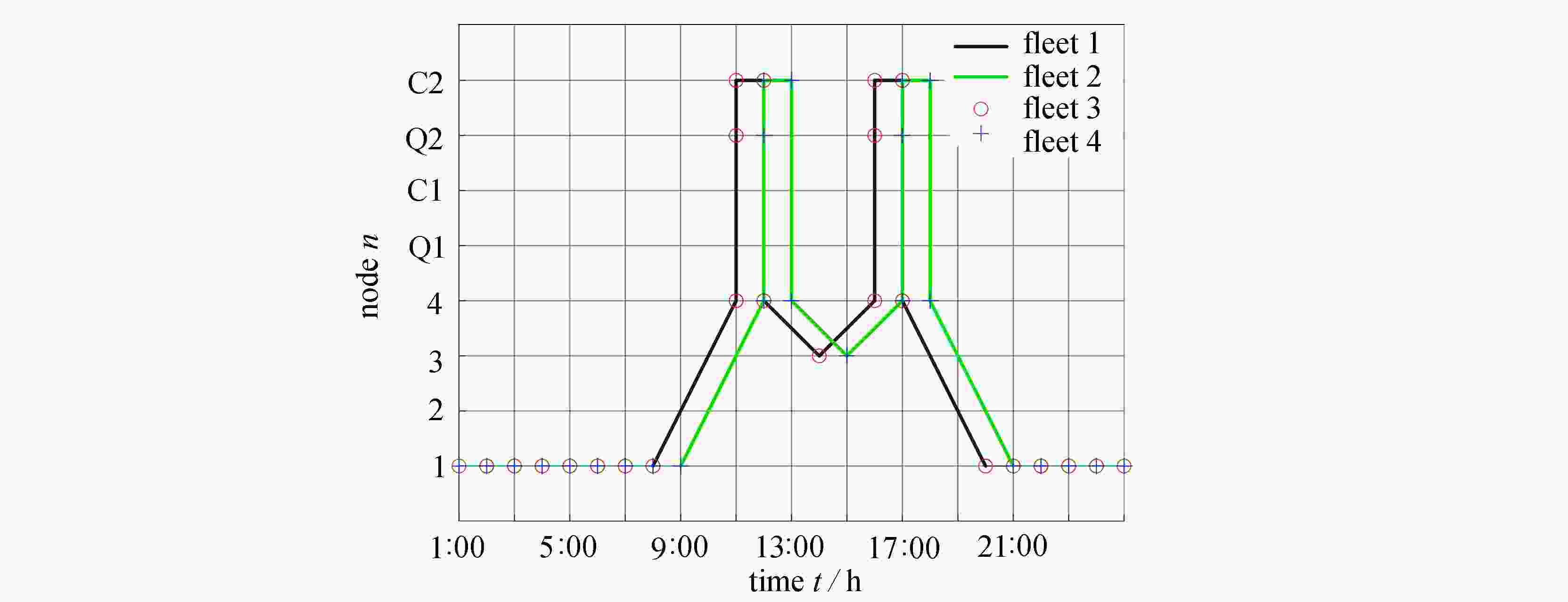
scenario total cost Ctotal /$ generation cost Cgeneration /$ carbon emission Mcarbon /t unmet traffic demand D 1 261 404.13 175 428.59 10588.12 0 2 287 652.67 166 613.51 11581.17 5400 3 263 758.63 172 999.91 10869.30 500 4 271 298.96 169 484.63 12 292.40 400 5 287 657.34 167 446.14 11479.21 5400 6 287 713.96 167 626.16 11464.01 5400
下载: 导出CSV
表 4 测试系统2情景1不同车队下的计算时间与差距
Table 4. CPU time and gap under different size of fleets in scenario 1 for case 2
fleet number computing time t/s gap δ/% 8 <20 0 12 <30 0.03 16 < 30 0.03 20 < 50 0.03 24 <100 0.3 28 < 600 0.6
下载: 导出CSV
-
[1] 杨天宇, 郭庆来, 盛裕杰, 等. 系统互联视角下的城域电力-交通融合网络协同[J]. 电力系统自动化, 2020, 44(11): 1-9 doi: 10.7500/AEPS20190811001YANG Tianyu, GUO Qinglai, SHENG Yujie, et al. Coordination of urban integrated electric power and traffic network from perspective of system interconnection[J]. Automation of Electric Power Systems, 2020, 44(11): 1-9.(in Chinese) doi: 10.7500/AEPS20190811001 [2] 李秋硕, 肖湘宁, 郭静, 等. 电动汽车有序充电方法研究[J]. 电网技术, 2012, 36(12): 32-38 doi: 10.7500/AEPS20210312006LI Qiushuo, XIAO Xiangning, GUO Jing, et al. Research on scheme for ordered charging of electric vehicles[J]. Power System Technology, 2012, 36(12): 32-38.(in Chinese) doi: 10.7500/AEPS20210312006 [3] TONG Li, ZHAO Shen, JIANG Hang, et al. Multi-scenario and multi-objective collaborative optimization of distribution network considering electric vehicles and mobile energy storage systems[J]. IEEE Access, 2021, 9: 55690-55697. doi: 10.7500/AEPS20210315002 [4] 苏粟, 李玉璟, 夏明超, 等. 基于时空耦合特性的充电站运行状态预测[J]. 电力系统自动化, 2022, 46(3): 23-32SU Su, LI Yujing, XIA Mingchao, et al. Operation state prediction of charging station based on spatio-temporal coupling characteristics[J]. Automation of Electric Power Systems, 2022, 46(3): 23-32.(in Chinese) [5] WEI Wei, MEI Shengwei, WU Lei, et al. Optimal traffic-power flow in urban electrified transportation networks[J]. IEEE Transactions on Smart Grid, 2017, 8(1): 84-95. doi: 10.1109/TSG.2016.2612239 [6] 谢仕炜, 林伟伟, 张亚超. 基于变分不等式理论的电力-交通耦合网络均衡状态研究[J]. 中国电机工程学报, 2022, 42(17): 6220-6239XIE Shiwei, LIN Weiwei, ZHANG Yachao. Research on coupled power-transportation network equilibrium state based on variational inequality theory[J]. Proceedings of the CSEE, 2022, 42(17): 6220-6239.(in Chinese) [7] LV Si, WEI Zhinong, SUN Guoqiang, et al. Optimal power and semi-dynamic traffic flow in urban electrified transportation networks[J]. IEEE Transactions on Smart Grid, 2019, 11(3): 1854-1865. [8] ZHOU Zhe, ZHANG Xuan, GUO Qinglai, et al. Analyzing power and dynamic traffic flows in coupled power and transportation networks[J]. Renewable and Sustainable Energy Reviews, 2021, 135: 110083. doi: 10.1016/j.rser.2020.110083 [9] 张鹏, 吕瑜佩, 郭明旻, 等. 简单闭环路网交通流定常解[J]. 应用数学和力学, 2021, 42(2): 123-132ZHANG Peng, LÜ Yupei, GUO Mingmin, et al. Steady-state solutions of traffic flow in a simple circled road network[J]. Applied Mathematics and Mechanics, 2021, 42(2): 123-132.(in Chinese) [10] ESTANDIA A, SCHIFFER M, ROSSI F, et al. On the interaction between autonomous mobility on demand systems and power distribution networks: an optimal power flow approach[J]. IEEE Transactions on Control of Network Systems, 2021, 8(3): 1163-1176. doi: 10.1109/TCNS.2021.3059225 [11] LIU Xiaochuan, SOH C B, ZHAO Tianyang, et al. Stochastic scheduling of mobile energy storage in coupled distribution and transportation networks for conversion capacity enhancement[J]. IEEE Transactions on Smart Grid, 2021, 12(1): 117-130. doi: 10.1109/TSG.2020.3015338 [12] LI Nan, UÇKUN C, CONSTANTINESCU E M, et al. Flexible operation of batteries in power system scheduling with renewable energy[J]. IEEE Transactions on Sustainable Energy, 2015, 7(2): 685-696. [13] 赵天阳, 张华君, 徐岩, 等. 不确定环境下含云计算数据中心的电网韧性增强调度[J]. 电力系统自动化, 2021, 45(3): 49-57ZHAO Tianyang, ZHANG Huajun, XU Yan, et al. Resilience-enhanced scheduling of power system with cloud computing data centers under uncertainty[J]. Automation of Electric Power Systems, 2021, 45(3): 49-57.(in Chinese) [14] RAHMANI M, KARGARIAN A, HUG G. Comprehensive power transfer distribution factor model for large-scale transmission expansion planning[J]. IET Generation, Transmission & Distribution, 2016, 10(12): 2981-2989. [15] ZHONG Shaopeng, JIANG Yu, NIELSEN O A. Lexicographic multi-objective road pricing optimization considering land use and transportation effects[J]. European Journal of Operational Research, 2022, 298(2): 496-509. doi: 10.1016/j.ejor.2021.05.048 [16] MARLER R T, ARORA J S. The weighted sum method for multi-objective optimization: new insights[J]. Structural and Multidisciplinary Optimization, 2010, 41(6): 853-862. doi: 10.1007/s00158-009-0460-7 [17] CHAKIROV A, FOURIE P J. Enriched Sioux Falls scenario with dynamic and disaggregate demand[J]. Arbeitsberichte Verkehrs-und Raumplanung, 2014: 978. doi: 10.3929/ethz-b-000080996 [18] 张展鹏, 班明飞, 郭丹阳, 等. 适用于环境-经济调度研究的燃煤机组二氧化碳排放特性模型[J]. 上海交通大学学报, 2021, 55(12): 1663-1672 doi: 10.16183/j.cnki.jsjtu.2021.368ZHANG Zhanpeng, BAN Mingfei, GUO Danyang, et al. A model for carbon diosixde emission characteristics of coal-fired unit for environment-economic dispatch research[J]. Journal of Shanghai Jiaotong University, 2021, 55(12): 1663-1672.(in Chinese) doi: 10.16183/j.cnki.jsjtu.2021.368 [19] 肖勇, 喻洁, 张新森, 等. 泛在电力物联网下用户侧分布式电源P2P优化调度研究[J]. 应用数学和力学, 2020, 41(12): 1358-1368XIAO Yong, YU Jie, ZHANG Xinsen, et al. Research on P2P optimal scheduling of user side distributed generation under ubiquitous power internet of things[J]. Applied Mathematics and Mechanics, 2020, 41(12): 1358-1368.(in Chinese) -
计量
- 文章访问数: 574
- HTML全文浏览量: 249
- PDF下载量: 60
- 被引次数: 0
渝公网安备50010802005915号