温差影响下的局部滑移接触行为的研究

杨阳; 王凯模; 沈火明; 王宇星

doi:10.21656/1000-0887.430334

温差影响下的局部滑移接触行为的研究

doi: 10.21656/1000-0887.430334

杨阳^1,,
王凯模¹,
沈火明^1, ,,
王宇星^{1, 2}

1.
西南交通大学力学与航空航天学院，成都 611756
2.
西南交通大学机械工程学院，成都 610031

基金项目: 国家自然科学基金(面上项目)（11672252）；中央高校基本科研费(科技创新项目)（2682022CX056）

详细信息

作者简介:
杨阳（1998—），男，硕士生（E-mail：249037911@qq.com）

沈火明（1968—），男，教授（通讯作者. E-mail：hmshen@126.com）

中图分类号: TH117; O343.6
计量
- 文章访问数: 622
- HTML全文浏览量: 308
- PDF下载量: 93
- 被引次数: 0
出版历程
- 收稿日期: 2022-10-21
- 修回日期: 2022-12-26
- 网络出版日期: 2023-02-09
- 刊出日期: 2023-02-15

Research on Partial Slip Contact Behaviors Under Temperature Effects

YANG Yang^1
,,
WANG Kaimo¹,
SHEN Huoming^{1
, ,},
WANG Yuxing^{1, 2}

1.
School of Mechanics and Aerospace Engineering, Southwest Jiaotong University, Chengdu 611756, P.R.China
2.
School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, P.R.China

摘要

摘要:
针对不同温度装配件间接触界面的局部滑移问题，建立了三维稳态热弹性局部滑移接触的半解析求解模型。基于热弹性理论与热传导方程，构建了半空间受热流载荷和力载荷作用下的频响函数并建立了相应的影响系数矩阵。借助离散卷积-快速Fourier变换等数学工具，实现了针对高温压头与热弹性半空间局部滑移接触问题的高效求解。接触界面间的热量传递满足Fourier热传导定律，并且黏/滑状态由Coulomb定律确定。基于该半解析模型分析了不同荷载及温差对表面法向压力分布、摩擦力分布、刚体位移及接触区黏/滑演化行为的影响。研究结果表明，当法向荷载和切向荷载一定时，温差的上升会导致接触区域的减小，引起接触面法向压力及摩擦力的峰值增大，并且会显著影响黏着区与滑移区的分布情况。
- 热弹性接触 /
- 局部滑移 /
- 半解析法 /
- 离散卷积-快速Fourier变换 /
- 共轭梯度法
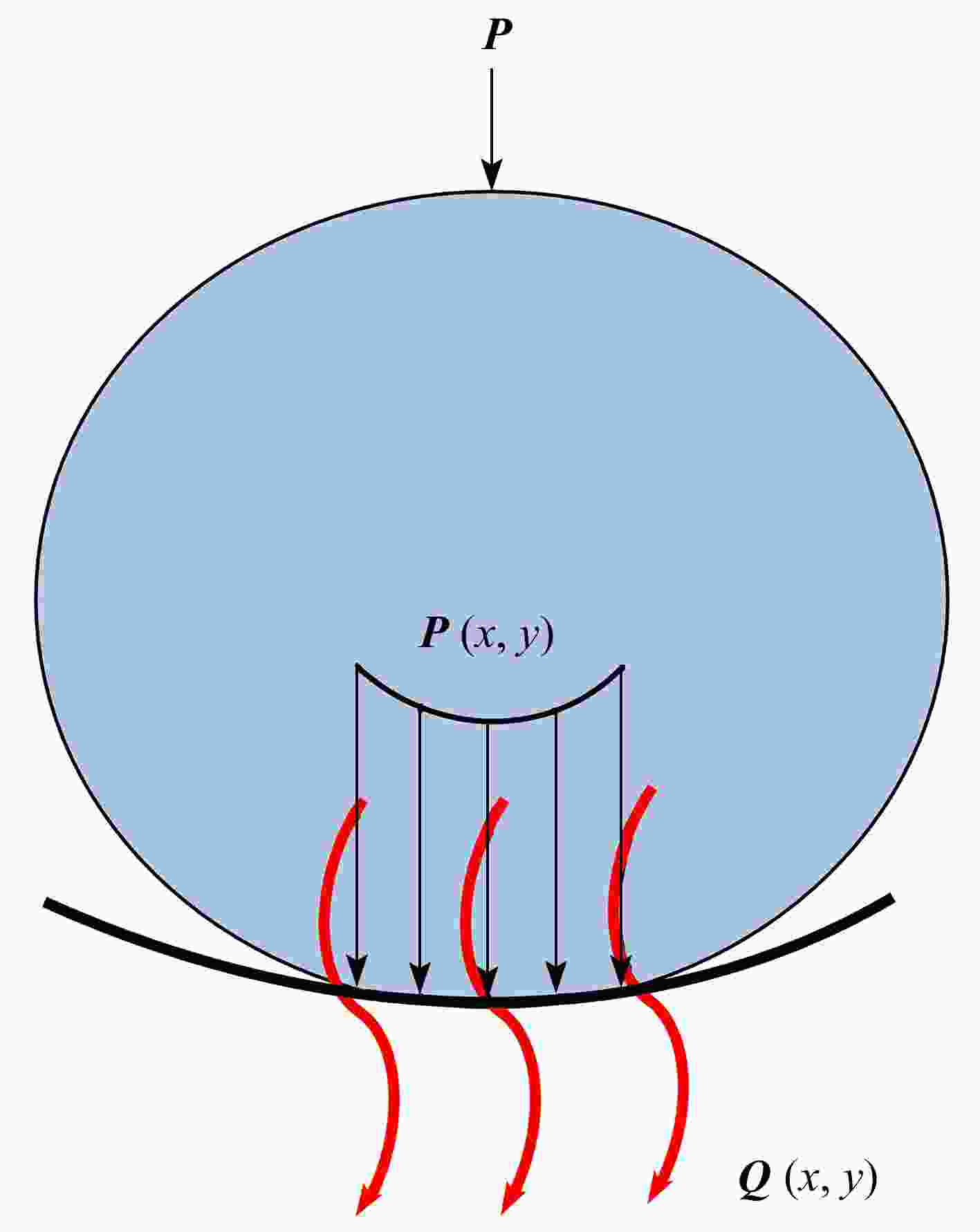
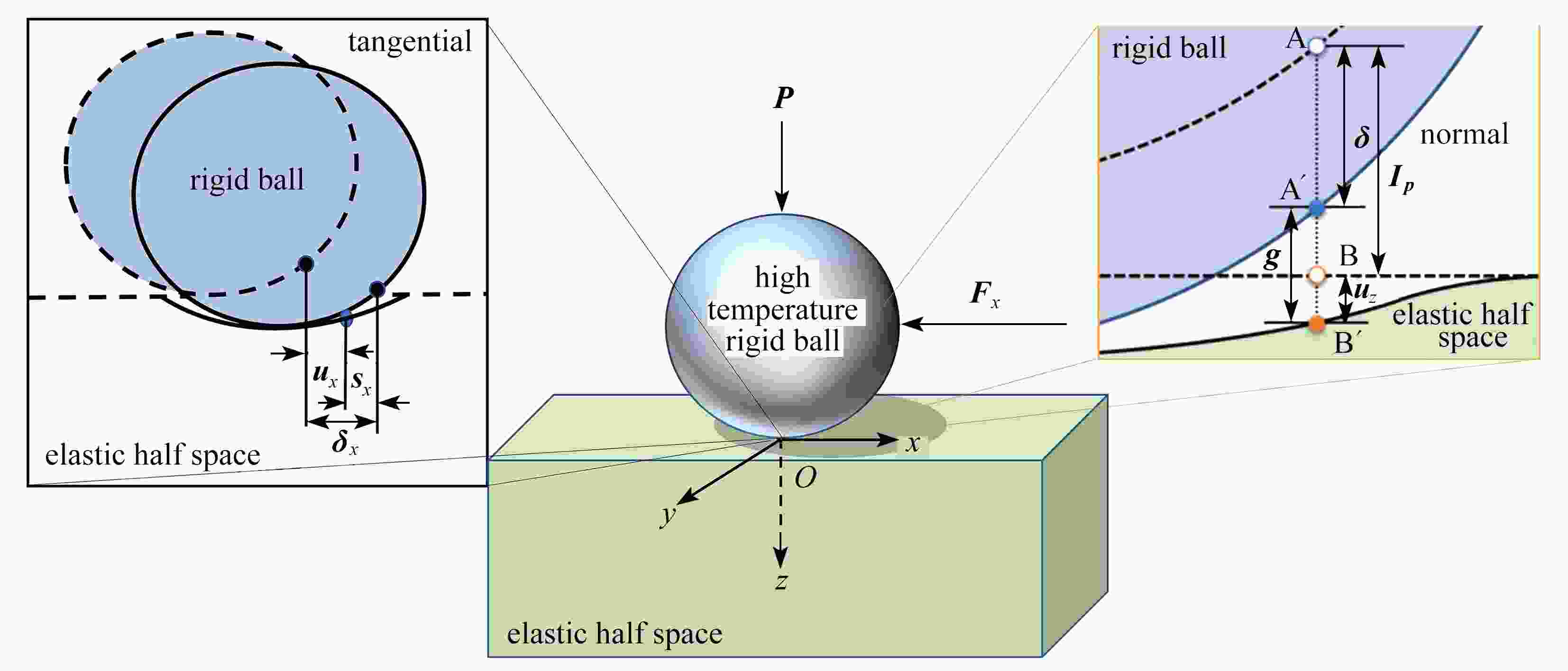
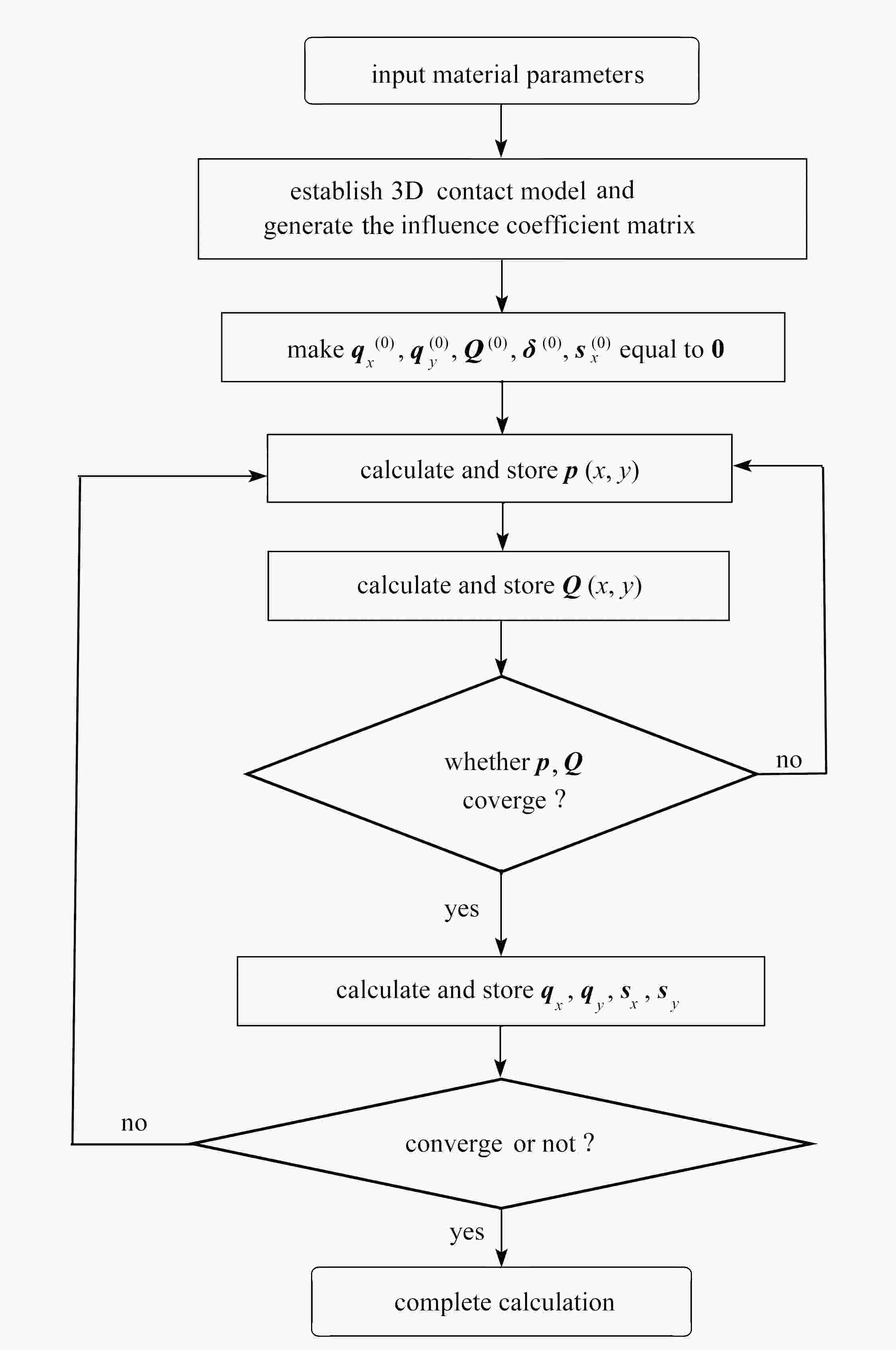
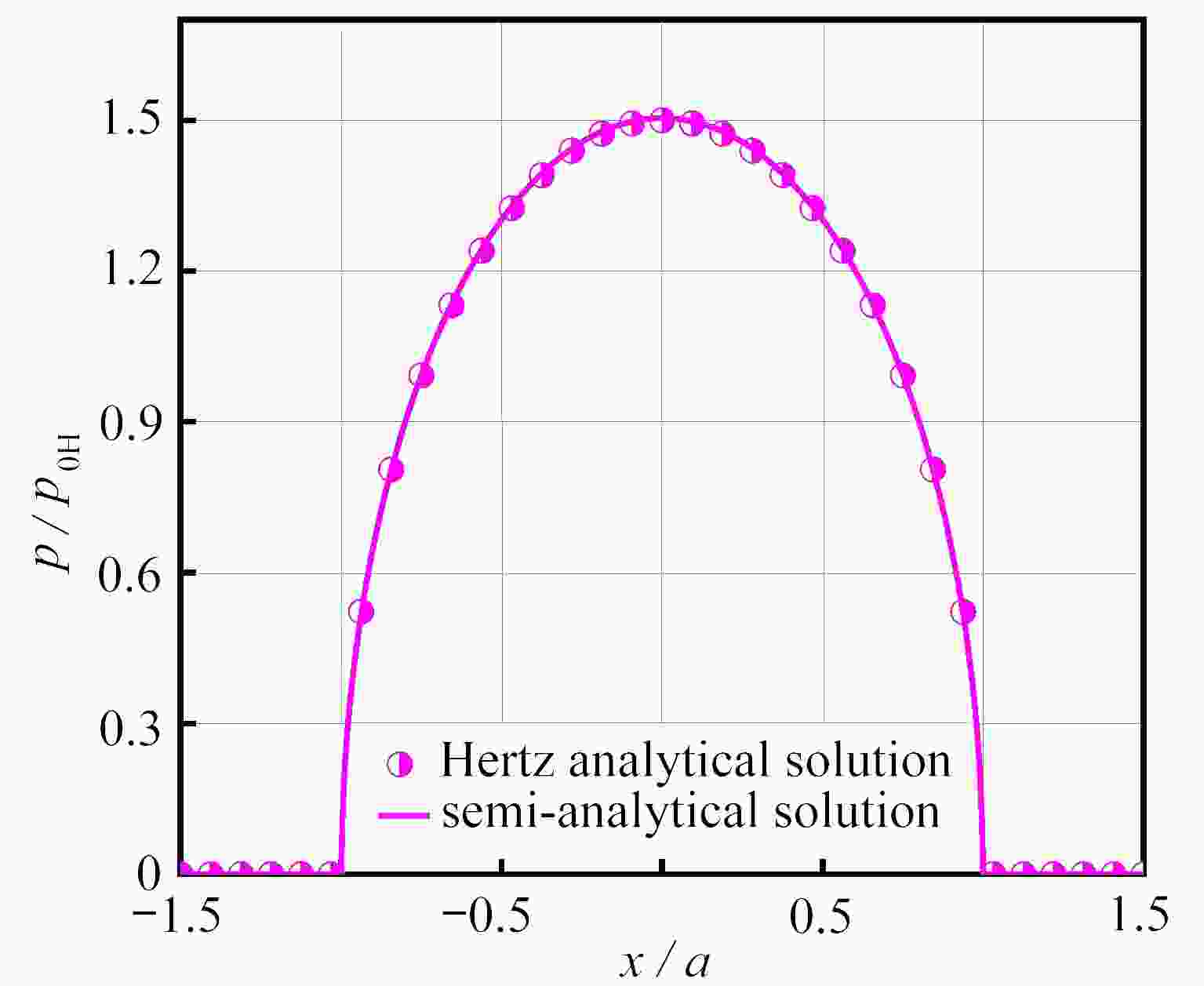
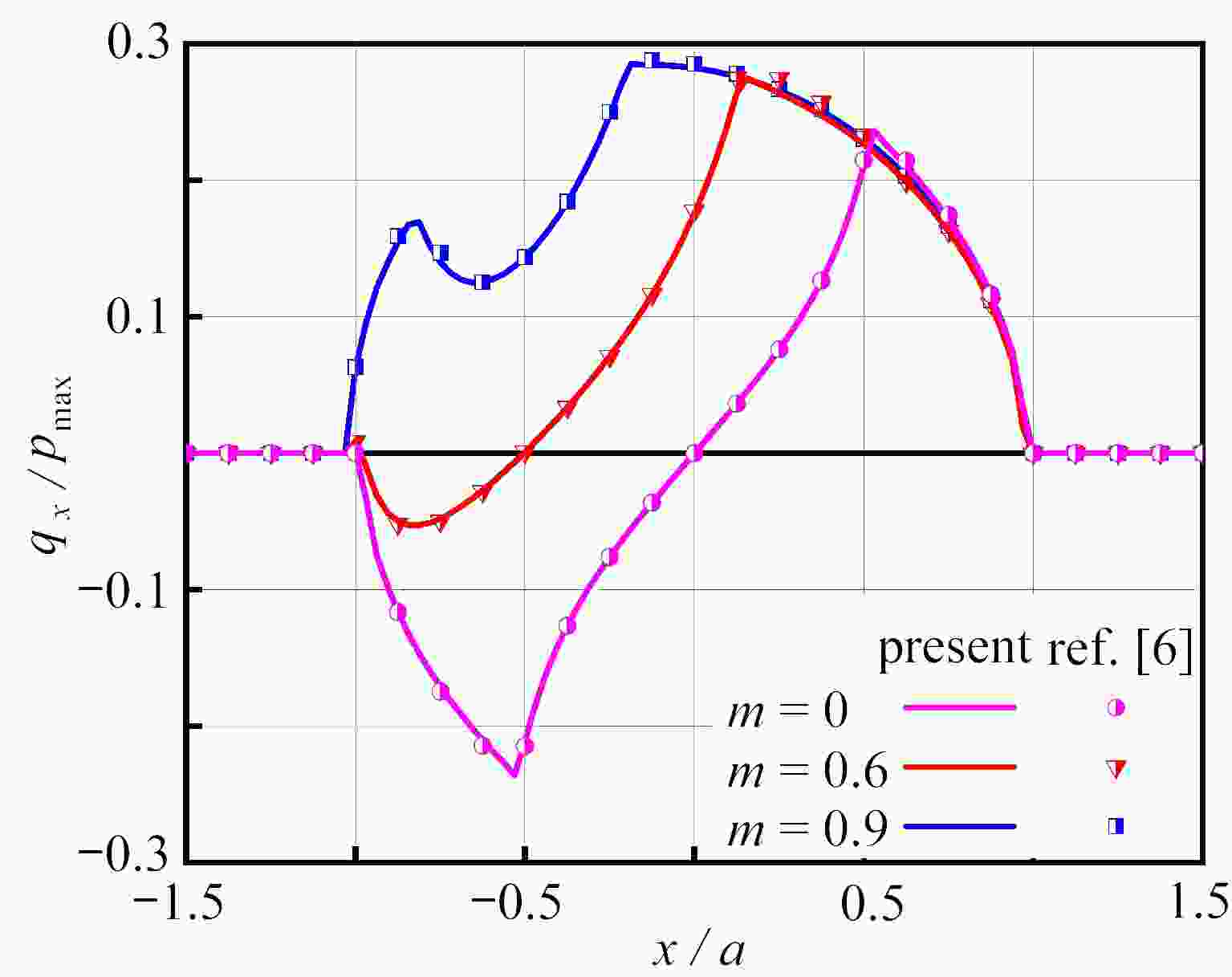
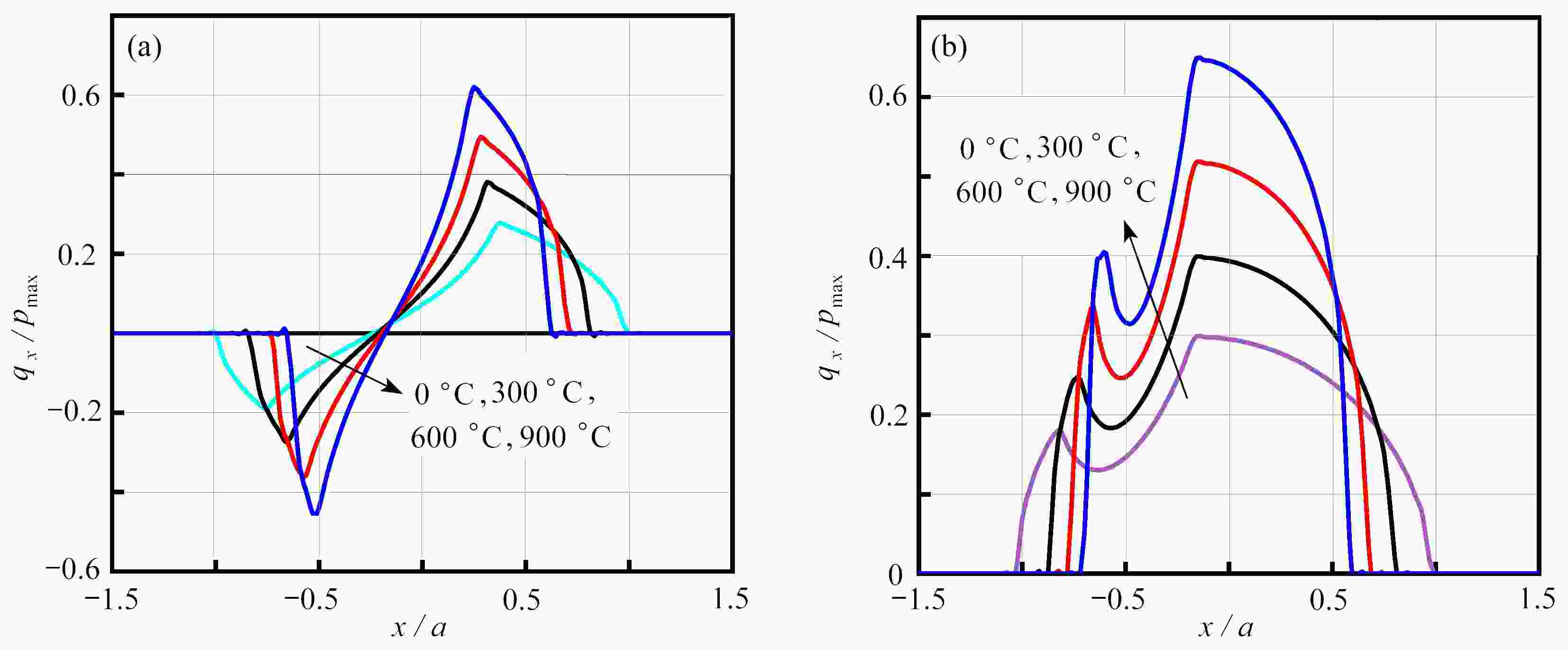
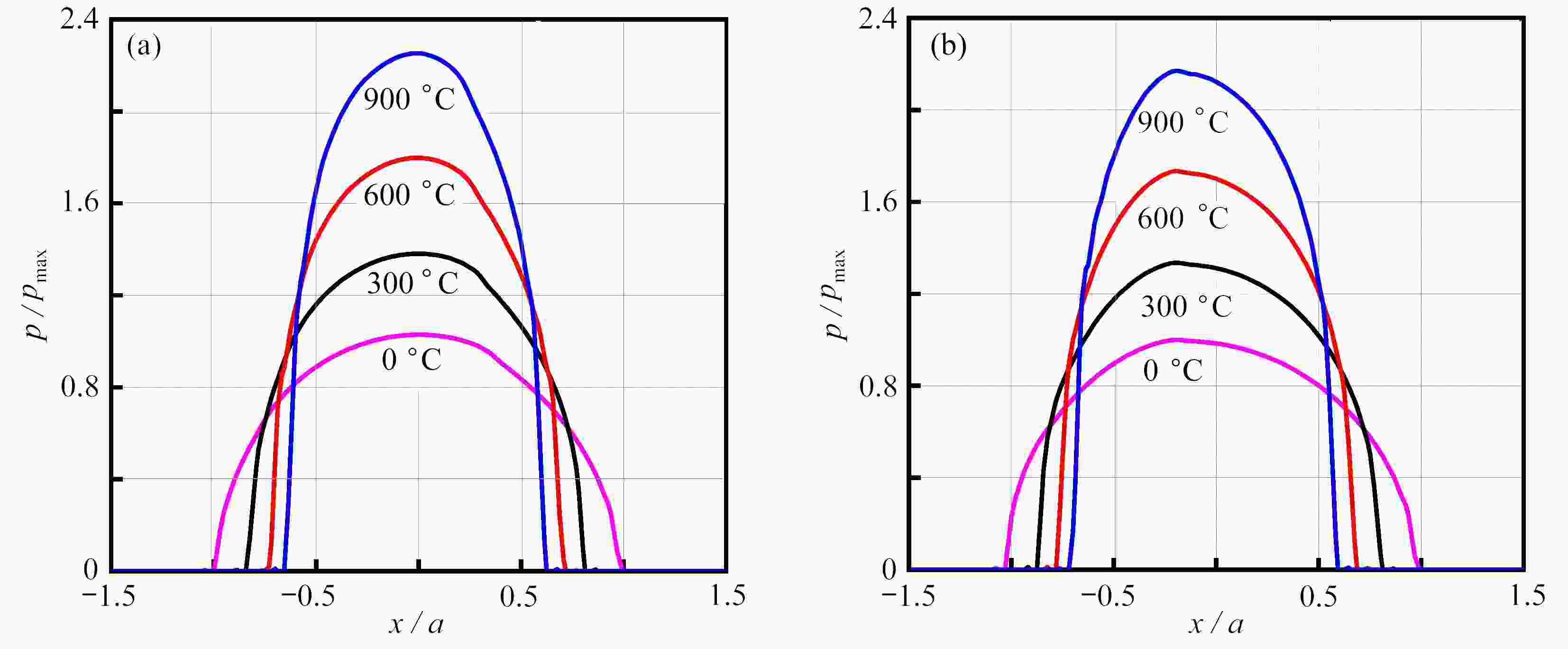
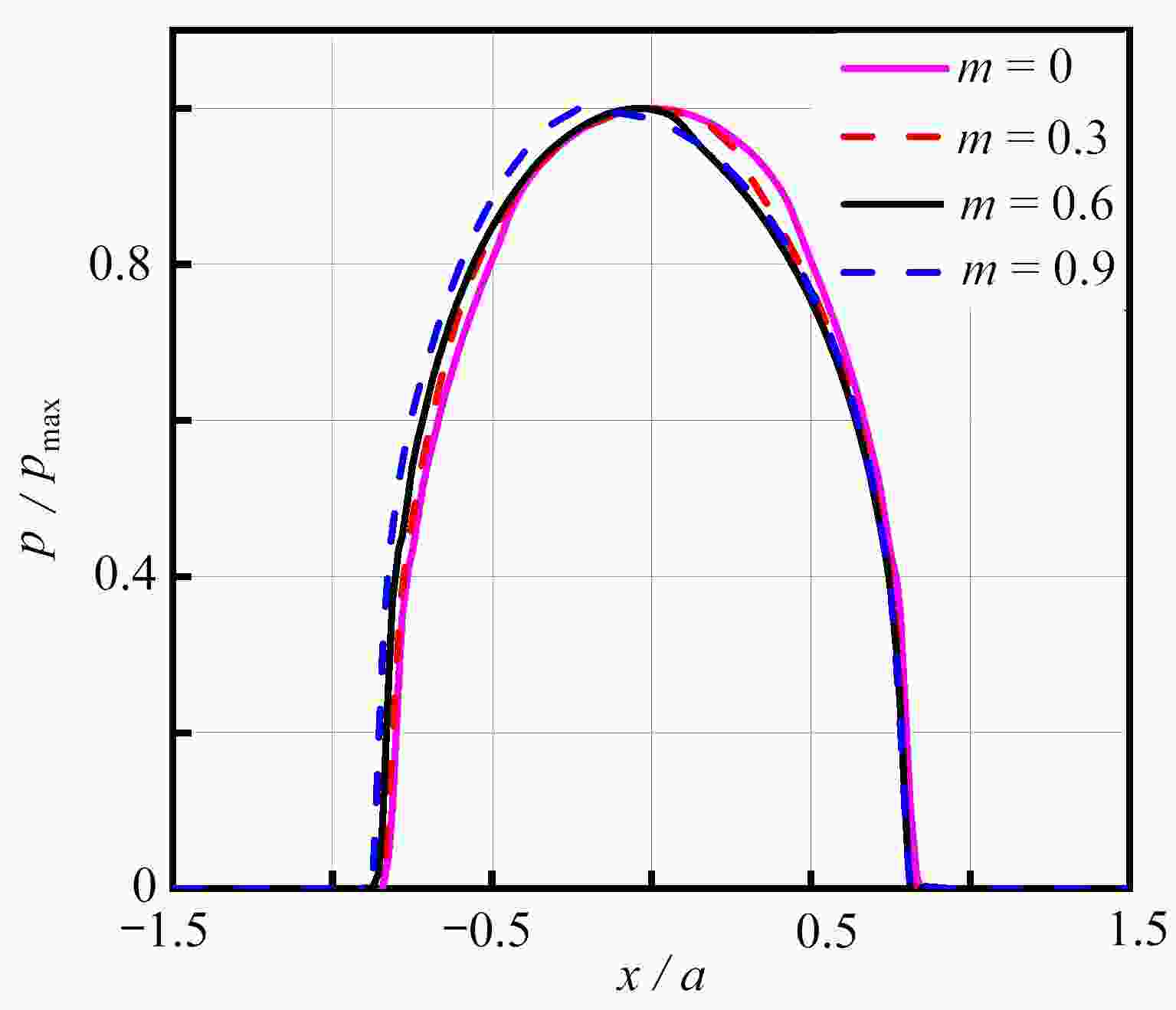
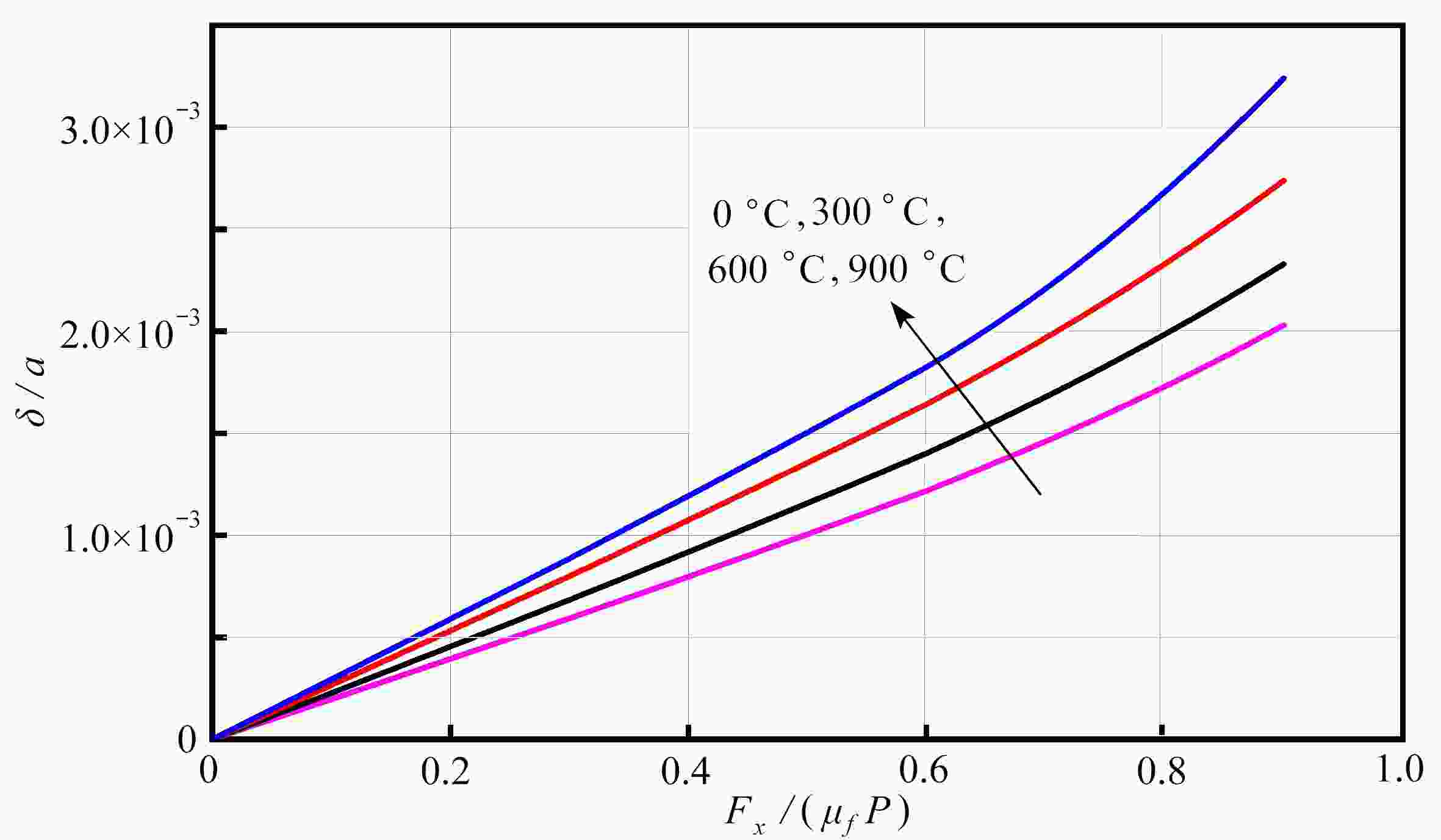
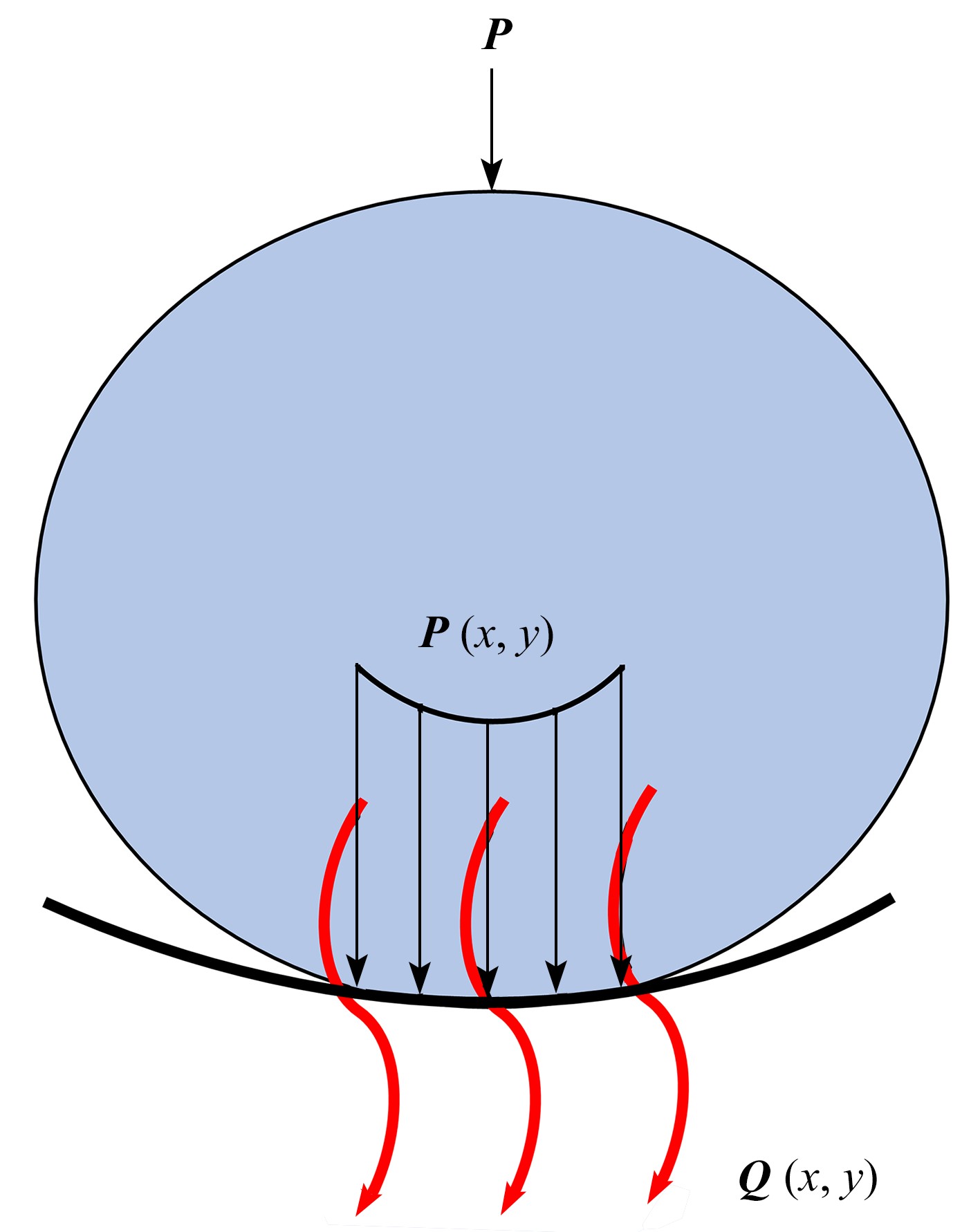
Abstract:
Aimed at the partial slip problem of contact interface between assemblies at different temperatures, a semi-analytical model for 3D steady-state thermoelastic partial slip contact was established. Based on the thermoelastic theory and the heat conduction equation, the frequency response functions of the half space under heat flux and force load were given, and the corresponding influence coefficients were established. With the discrete convolution and fast Fourier transform (DC-FFT), the partial contact between the rigid high-temperature indenter and the thermoelastic half space was efficiently solved. The heat conduction behavior was assumed to follow Fourier’s law, and the stick/slip state on the contact interface was determined under Coulomb’s law. Based on this semi-analytical model, the effects of external loads and temperature differences on the surface pressure distribution, the friction distribution, the rigid body displacement, and the stick/slip evolution behaviors, were analyzed in detail. The numerical results show that, the increase of the temperature difference will lead to a decrease of the contact area, result in an increase of the peak values of the normal pressure and the friction, and significantly influence the regions of the stick zone and the slip zone.
- thermoelastic contact /
- partial slip /
- semi-analytical method /
- discrete convolution and fast Fourier transform /
- conjugate gradient method

HTML全文

图 1 热流作用示意图

Figure 1. Diagram of the heat flow action

下载: 全尺寸图片幻灯片

图 2 三维接触模型示意图

Figure 2. Schematic diagram of the 3D contact model

下载: 全尺寸图片幻灯片

图 3 流程图

Figure 3. The flow chart

下载: 全尺寸图片幻灯片

图 4 半解析法向压力p沿x轴方向的分布与Hertz解析解的对比

Figure 4. Comparison between the distribution of semi-analytical normal pressure p along the x-axis and the Hertz analytical solution

下载: 全尺寸图片幻灯片

图 5 切向力${q_x}$沿x轴方向的分布

Figure 5. The distribution of tangential force ${q_x}$ along the x-axis

下载: 全尺寸图片幻灯片

图 6 不同温差、切向荷载下，无量纲切向力沿x轴方向的分布：(a) ${F_x} = 0.3\mu _f P$；(b) ${F_x} = 0.9\mu _f P$

Figure 6. Distributions of the dimensionless tangential force along the x-axis under different temperature rises and tangential loads: (a) ${F_x} = 0.3\mu _f P$; (b) ${F_x} = 0.9\mu _f P$

下载: 全尺寸图片幻灯片

图 7 不同温差、切向荷载下，无量纲法向压力沿x轴方向的分布：(a) ${F_x} = 0.3\mu _fP$；(b) ${F_x} = 0.9\mu _fP$

Figure 7. Distributions of the dimensionless normal pressure along the x-axis under different temperature rises and tangential loads: (a) ${F_x} = 0.3\mu _fP$; (b) ${F_x} = 0.9\mu _f P$

下载: 全尺寸图片幻灯片

图 8 300 ℃温差下不同切向荷载作用下法向压力沿x轴方向的分布

Figure 8. Distributions of the normal pressure along the x-axis under different tangential loads at a temperature rise of 300 ℃

下载: 全尺寸图片幻灯片

图 9 不同温差下刚体位移与切向荷载的关系

Figure 9. Relationships between the rigid body displacement and the tangential load at different temperatures rises

下载: 全尺寸图片幻灯片

图 10 不同切向荷载下黏/滑比与温差的关系

Figure 10. Relationships between the stick/slip ratio and the temperature under different tangential loads

下载: 全尺寸图片幻灯片

表 1 模型参数

Table 1. Model parameters

model parameter	value
normal load $P/{\rm{N}}$	20
tangential load ${F_x}/{\rm{N}}$	$\left( {0 \sim 0.9} \right) \times {\mu _f}P$
tangential load ${F_y}/{\rm{N}}$	0
friction coefficient ${\mu _f}$	0.3
ball radius $R/{\rm{mm}}$	18
maximum Hertzian pressure ${p_{\max } }/{\rm{MPa}}$	907
elastic half space modulus $E/{\rm{GPa}}$	210
Poisson’s ratio of elastic half space $\nu $	0.3
thermal expansion in coefficient elastic half space K	$2.0 \times {10^{ - 5}}$
elastic half space heat transfer coefficien $Q/({{\text{W}}/ {({\text{m}} \cdot {\text{K}})}}$)	60

下载: 导出CSV

参考文献(16)

[1]	JOHNSON K L. Contact Mechanics[M]. Cambridge, UK: Cambridge University Press, 1985.
[2]	LAKKARAJU R K, BOBARU F, ROHDE S L. Optimization of multilayer wear-resistant thin filmsusing finite element analysis on stiff and compliantsubstrates[J]. Journal of Vacuum Science & Technology A, 2006, 24(1): 146-155.
[3]	潘先云, 余江鸿, 周枫林. 非齐次弹性力学问题双互易边界元方法研究[J]. 应用数学和力学, 2022, 43(9): 1004-1015 PAN Xianyun, YU Jianghong, ZHOU Fenglin. Research on the dual reciprocity boundary element method for non-homogeneous elasticity problems[J]. Applied Mathematics and Mechanics, 2022, 43(9): 1004-1015.(in Chinese)
[4]	王晋宝, 童焯煜, 何博, 等. 考虑应力沿深度变化的饱和软黏土一维固结半解析解[J]. 应用数学和力学, 2019, 40(10): 1099-1108 WANG Jinbao, TONG Zhuoyu, HE Bo, et al. A semi-analytical 1D consolidation solution of saturated soft clay with changing stresses along the depth[J]. Applied Mathematics and Mechanics, 2019, 40(10): 1099-1108.(in Chinese)
[5]	KUPCHYTSR, BAJKOWSKIA. Elastic coating within homogeneous inter layer under the action of normal and tangential forces[J]. Materials Science, 2014, 49(5): 650-659. doi: 10.1007/s11003-014-9659-x
[6]	WANG Z J, WANG W Z, WANG H, et al. Partial slip contact analysis on three-dimensional elastic layered half space[J]. Journal of Tribology, 2010, 132(2): 021403. doi: 10.1115/1.4001011
[7]	CHEN W, WANG Q J. A numerical static friction model for spherical contacts of rough surfaces, influence of load, material, and roughness[J]. Journal of Tribology, 2009, 131(2): 021402. doi: 10.1115/1.3063814
[8]	WANG Z J, JIN X, LIU S B, et al. A new fast method for solving contact plasticity and its application in analyzing elasto-plastic partial slip[J]. Mechanics of Materials, 2013, 60: 18-35. doi: 10.1016/j.mechmat.2013.01.001
[9]	WANG Z J, MENG F M, XIAO K, et al. Numerical analysis of partial slip contact under a tangential force anda twisting moment[J]. Proceedings of the Institution of Mechanical Engineers (Part J): Journal of Engineering Tribology, 2011, 225(2): 72-83. doi: 10.1177/2041305X10392125
[10]	向金兰, 刘娟, 沈火明. 热源影响下的涂层板滑动接触问题研究[J]. 机械科学与技术, 2021, 40(2): 165-167 doi: 10.13433/j.cnki.1003-8728.20200040 XIANG Jinlan, LIU Juan, SHEN Huoming. Study on sliding contact problem of coated plate considering heat source[J]. Mechanical Science and Technology, 2021, 40(2): 165-167.(in Chinese) doi: 10.13433/j.cnki.1003-8728.20200040
[11]	李玲, 田海飞, 云强强, 等. 微动接触中分形粗糙表面的温升分布研究[J]. 表面技术, 2019, 48(6): 238-244 doi: 10.16490/j.cnki.issn.1001-3660.2019.06.028 LI Ling, TIAN Haifei, YUN Qiangqiang, et al. Temperature rise distribution of fractal rough surface in fretting contact[J]. Surface Technology, 2019, 48(6): 238-244.(in Chinese) doi: 10.16490/j.cnki.issn.1001-3660.2019.06.028
[12]	ZHANG X, SHEN H M, LIU J, et al. An efficient numerical model for predicting the torsional fretting wear considering real rough surface[J]. Wear, 2015, 344/345: 32-45. doi: 10.1016/j.wear.2015.10.019
[13]	ZHANG X, WANG Z J, SHEN H M, et al. Dynamic contact in multiferroic energy conversion[J]. International Journal of Solids and Structures, 2018, 143: 84-102. doi: 10.1016/j.ijsolstr.2018.02.034
[14]	LIU S, WANG Q. Studying contact stress fields caused by surface tractions with a discrete convolution and fast Fourier transform algorithm[J]. Journal of Tribology, 2002, 124(1): 36-45. doi: 10.1115/1.1401017
[15]	POLONSKY I A, KEER L M. A numerical method for solving rough contact problems based on the multi-level multi-summation and conjugate gradient techniques[J]. Wear, 1999, 231(2): 206-219. doi: 10.1016/S0043-1648(99)00113-1
[16]	王宇星. 三维偶应力弹性体接触力学问题的半解析法建模研究[D]. 博士学位论文. 成都: 西南交通大学, 2021. WANG Yuxing. Semi-analytical modeling of three-dimensional contact problem within the framework[D]. PhD Thesis. Chengdu: Southwest Jiaotong University, 2021. (in Chinese)