Topology Optimization Design of Heat Convection Problems With Variable-Density Cells
-
摘要: 为获得优异的散热结构设计，发展了一种基于腐蚀-扩散算子的变密度胞元层级结构设计方法. 通过腐蚀-扩散算子得到了一系列拓扑相似但体积分数不同的变密度微结构，计算并拟合得到变密度微结构等效热传导系数曲线. 在此基础上，采用移动渐近线法更新宏观设计变量，将变密度微结构植入相应体积分数的宏观单元中完成装配. 通过数值算例对不同优化方法下温度场的热柔顺度、平均温度、方差等参数进行了比较分析，结果表明，变密度胞元层级结构比传统单尺度胞元结构和周期胞元结构具有更好的散热性能.Abstract: The method of designing cell structures with variable-density cells based on erode-dilate operators was applied to the optimization of thermal structures. A series of variable-density microstructures with the same topology definition but different volume fractions were obtained with erode-dilate operators. Then, the thermal conductivity of the variable-density cells was extracted and the equivalent thermal conductivity fitting curve was obtained. After this, the method of moving asymptotes was used to update macro design variables, and the variable-density microstructure was implanted into the macroscopic unit of the corresponding volume fraction to complete the assembly. Numerical examples were given to compare and analyze the thermal compliance, the mean temperature, the variance and other parameters of the temperature fields with different optimization methods. The results show that, variable-density cell structures have better heat dissipating performance than traditional single-scale cell structures and periodic cell structures.
-
0. 引言
低温环境是确保电子设备、发动机、航天飞机和卫星等系统安全工作的必要条件之一. 因此，结构散热一直以来都是学者和工程师研究和设计的热点[1]. 其中，热传导系统具有加工简单、不依赖其他电子系统、无噪声等优点，在工业应用中最为广泛. 随着设备精度的不断提升，研究微型化、轻量化、高效化的散热系统至关重要.
拓扑优化是一种新型的结构优化设计方法，其不依赖于工程经验就能得到意想不到的创新构型，被广泛应用于基于热传导、热对流和共轭传热的热系统优化[2-3]. 然而，这些研究大多只是在宏观尺度上进行结构优化，设计空间有限. 在自然界中，植物茎和动物骨骼等生物结构多是由胞元结构组成，具有高刚度、耐腐蚀、多功能和轻量化等优越的性能[4]. 受这一现象的启发，结构的宏观和微观一体化拓扑优化设计受到了研究者们的关注.
多尺度拓扑优化设计可以追溯到Rodrigues等[5]提出的宏观尺度材料分布和微结构设计协同优化的层级算法. Xia和Breitkopf[6-7]将非线性FE2框架应用于多尺度设计. 然而，这些设计中每个单元的微结构都不同，计算成本高，且难以制造. 为此，Liu和Cheng等[8-9]提出了一种并行拓扑优化方法来设计周期胞元结构，只需求解一个简单的优化公式，大幅缩减了计算成本. Long等[10]将这种方法应用于考虑承载能力和保温性能的结构轻量化设计. Yan和Huang等[11]解决了以宏观结构刚度和材料导热系数为目标函数的多目标多尺度结构优化问题. Yan等[12]证实，对于热弹性问题，周期胞元结构比宏观结构表现出更好的性能. 但由于微观结构相同，设计空间有限，只能获得很小的性能改进.
变密度胞元结构[13]是另一种特殊类型的多尺度结构，其微结构具有相似的拓扑结构，仅一个或多个几何参数在宏观设计域内变化. 通过优化这些几何参数，可以将不同密度的微结构置于最佳宏观位置. Wang等[14]通过优化不同六边形单胞的厚度，使结构的散热效率提高一倍. Cheng等[15-16]开发了一种网格密度填充和与设计相关的动态特征的并行优化方法. Wu等[17]开发了一种考虑尺度效应的带惩罚的简化子结构近似(ARSP)模型. 然而，在这些工作中，微观结构拓扑是规定的，而不是优化得到的.
在微观结构拓扑与宏观密度并行优化中，最困难的是如何提取一个参数来改变微结构的密度. 特别是在拓扑优化框架中，用元素密度或水平集函数描述微观结构拓扑，很难提取一个显式的参数，如半径或厚度. 最近，基于水平集框架，Wang等[18-19]提出了一种在不同位置切割带符号的距离函数的参数化方法. 在此基础上，Zong等[20]为保证相邻单元之间完美的几何连接，通过插值一组位于节点上的高度变量，构造了一个可变切割函数. 而后，一种类似的形状插值技术被提出来生成一系列基于参数水平集方法优化的微结构[21-22].
本文提出了一种实现微观结构拓扑与宏观密度并行拓扑设计的有效方法. 首先，在密度框架下优化具有不同体积分数的单一或有限种微结构; 然后应用腐蚀-扩散算子构建准周期微结构库; 最后，解决宏观热柔顺度最小问题，并将这些微结构置于宏观设计域.
1. 优化模型
1.1 变密度胞元结构
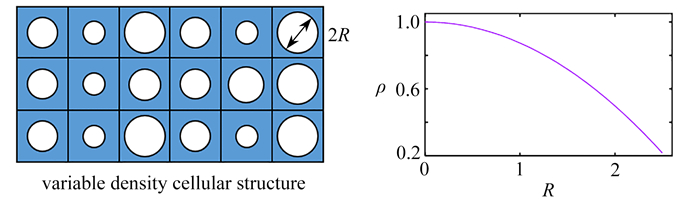
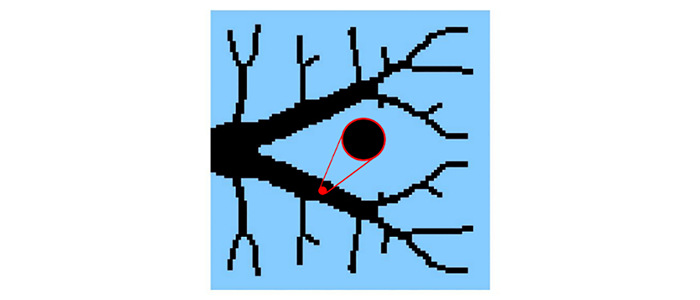
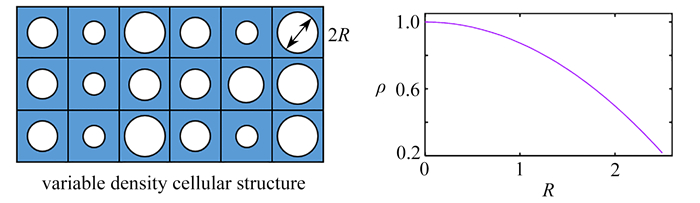
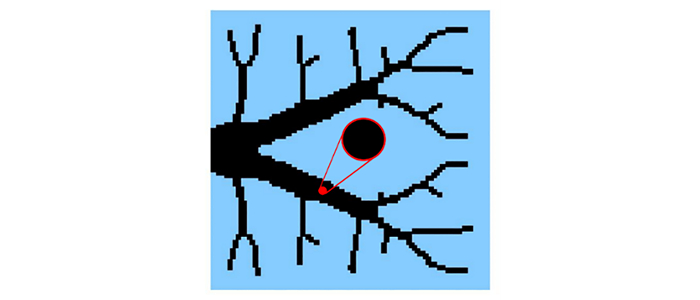
图 1为典型的变密度胞元结构，其微结构密度ρ由内孔半径R控制. 由于微结构拓扑是预定的，性能改进有限. 文献中有很多性能优异的微结构拓扑优化构型[23-27]，但其复杂的几何结构导致很难提取一个显式的几何参数来改变密度.
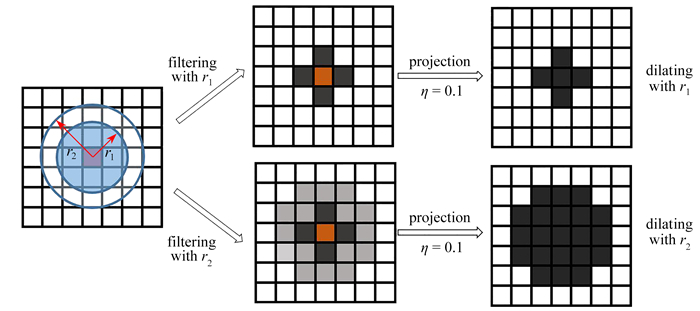
图 1 变密度胞元结构及其几何参数与密度的关系Figure 1. Illustration of the variable density cellular structure一些研究人员预先设计了一系列密度不等的微结构，并置于宏观设计域. 然而，这一过程计算成本很高，且不能保证相邻微结构之间的连通性. 为此，本文提出了一种基于腐蚀-扩散算子的方法来参数化微结构拓扑. 在基于密度的拓扑优化框架中， ρmi=[ρ1mi, ρ2mi, ⋯, ρNmimi]表示微结构拓扑. 结合密度滤波技术[28]，腐蚀-扩散算子可表示为
$$ \bar{\tilde{\rho}}_e^{\mathrm{mi}}=\frac{\tanh (\beta \eta)+\tanh \left(\beta\left(\tilde{\rho}_e^{\mathrm{mi}}-\eta\right)\right)}{\tanh (\beta \eta)+\tanh (\beta(1-\eta))}, $$ (1) 其中，$\tilde{\rho}_e^{\mathrm{mi}} $表示相邻设计变量ρemi的加权平均值：
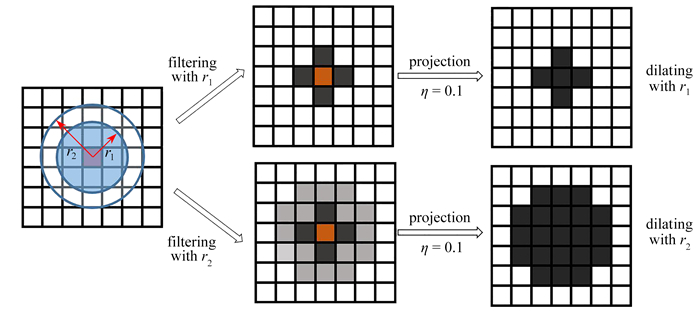
$$ \tilde{\rho}_e^{\mathrm{mi}}=\frac{\sum\limits_{i \in N_e} w\left(\boldsymbol{x}_i\right) v_i \rho_i^{\mathrm{mi}}}{\sum\limits_{i \in N_e} w\left(\boldsymbol{x}_i\right) v_i}. $$ (2) 式(2) 和(1) 分别表示过滤和映射过程, 简图如图 2所示. $\beta$代表映射方程的斜率, $\beta \rightarrow \infty$时映射方程是Heaviside方程, $\rho_i^{\mathrm{mi}}$和$v_i$分别代表第$i$个单元的密度和体积. $w\left(\boldsymbol{x}_i\right)=r_{\text {min }}-\left\|\boldsymbol{x}_i-\boldsymbol{x}_e\right\|$和$\boldsymbol{x}_i$是中心点的权函数和坐标向量. $N_e=\left\{i \mid\left\|\boldsymbol{x}_i-\boldsymbol{x}_e\right\| \leqslant r_{\min }\right\}$代表中心点周围圆形过滤区域内的相邻单元个数, $\|\cdot\|$代表 2范数, $r_{\min }$为过滤半径. $0 \leqslant \eta \leqslant 1$代表Heaviside方程的截断值: 密度大于$\eta$的灰色单元将被映射为$\bar{\tilde{\rho}}_e=1$, 其余的为$\bar{\tilde{\rho}}_e=0$. 这些微结构共享相似的拓扑结构, 从而确保了相邻微结构之间的自然连接.
1.2 优化流程
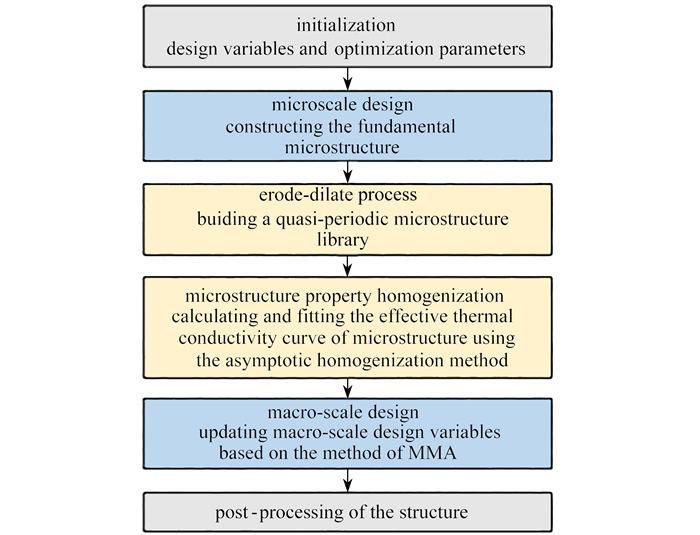
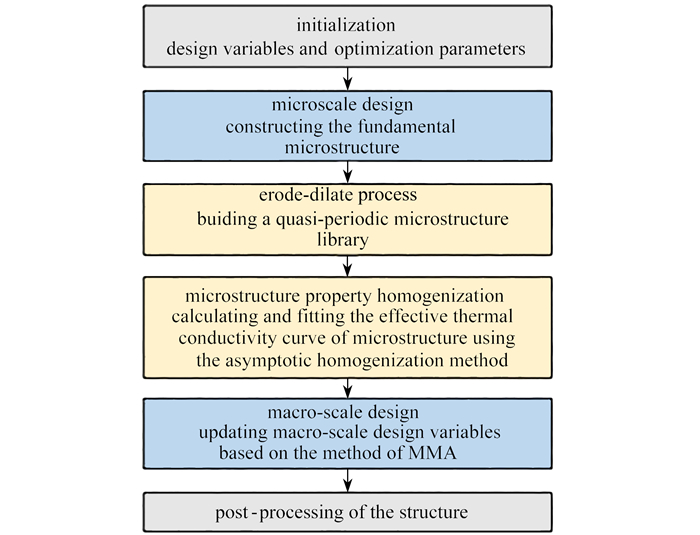
为了更清楚地说明本文提出的算法，本小节给出了热对流问题微观结构拓扑与宏观密度分布并行拓扑设计的具体优化流程，如图 3所示.
图 3 提出算法的优化流程图注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.Figure 3. The optimization flowchart of the proposed methodStep 1: 优化得到有限个体积分数不同的微结构；
Step 2: 基于腐蚀-扩散算子，建立准周期微结构库；
Step 3: 利用渐近均匀化方法计算微结构等效材料属性，及其B样条代理模型；
Step 4: 优化宏观单元的密度分布；
Step 5: 基于MMA优化算法更新设计变量，完成结构优化并进行后处理及验证.
2. 问题描述
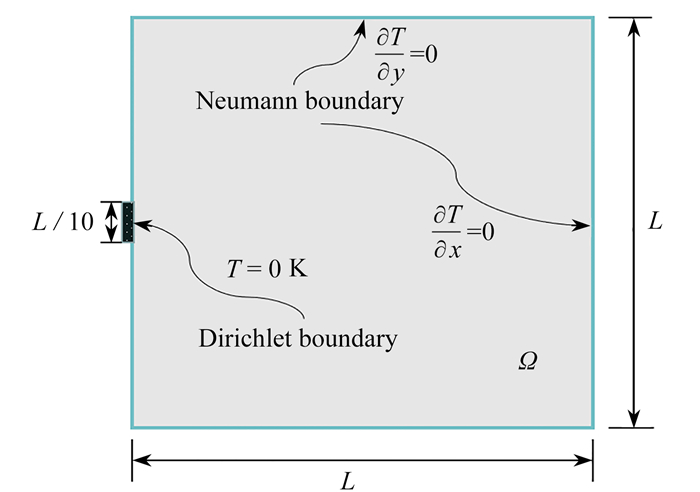
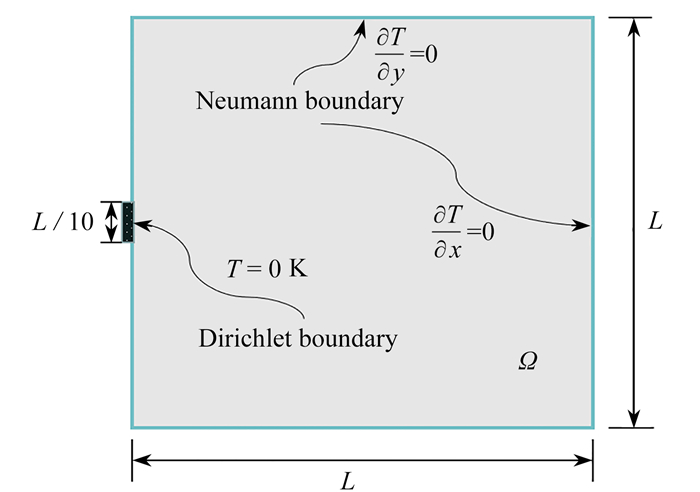
本节针对热传导问题验证本文算法的有效性，测试模型设计域为边长L=1 m的正方形，均布热载荷Q=1 W/m2. 规定左侧中部长度为L/10的边界T=0 K，其他边界对流系数为0(图 4).
网格划分规模为100×100. 为提高结构热导率，优化采用双材料，其导热系数分别为k1=1 W/(m2·K)和k2=0.001 W/(m2·K).
在稳态热传导问题中，结构热柔顺度被广泛用于性能评估. 结构的热柔顺度值越小，说明结构的导热性越好. 因此，本文考虑了体积约束下结构热柔顺度最小的优化问题：
$$ J=\boldsymbol{T}^{\mathrm{T}} \boldsymbol{K} \boldsymbol{T}, $$ (3) 其中，K和T分别表示全局热传导矩阵和温度向量，满足方程KT = Q，Q为热载荷向量. 矩阵K可由下式计算得到：
$$ \boldsymbol{K}=\sum\limits_{e=1}^{N^{\mathrm{ma}}} \boldsymbol{K}_e=\sum\limits_{e=1}^{N^{\mathrm{ma}}} \int_{\varOmega_e} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{D}_e \boldsymbol{B} \mathrm{d} \varOmega, $$ (4) 其中，Ωe和Nma分别表示单元积分域和单元个数，B是单元应变矩阵，De是位于第e个宏观单元的微结构的等效热传导系数矩阵.
本文基于渐近均匀化方法[29]计算微结构的等效矩阵:
$$ \boldsymbol{D}^{\mathrm{H}}=\frac{1}{|Y|} \int_Y\left[\boldsymbol{D}(y)-\boldsymbol{D}(y) \boldsymbol{\varepsilon}_y(\boldsymbol{\phi}, y)\right] \mathrm{d} y, $$ (5) 其中，D(y)是微观材料插值得到的热传导系数矩阵，y代表微观积分域，εy(·)是应变算子，ϕ =[ϕ11, ϕ22, ϕ12] 代表求解施加周期性边界条件的均匀化问题得到的三个特征位移场：
$$ \int_Y \boldsymbol{\varepsilon}_y^{\mathrm{T}}(\boldsymbol{v})\left[\boldsymbol{D}(y)-\boldsymbol{D}(y) \boldsymbol{\varepsilon}_y(\boldsymbol{\phi})\right] \mathrm{d} y=0, \quad \forall \boldsymbol{\phi} \in V_y, $$ (6) 其中，$V_y=\left\{u_y(y) \mid y \in Y, u_y(y+Y)=u_y(y)\right\} $表示单元Y中定义的周期函数的函数空间，v表示虚位移场.
3. 微观尺度设计
3.1 微观尺度优化模型
基于密度的拓扑优化方法，采用均匀化方法和MMA优化方法进行微观结构设计:
$$ \left\{\begin{array}{l} \text {find} \quad\boldsymbol{\rho}^{\mathrm{mi}}, \\ \min \quad J \\ \quad\;\;\boldsymbol{K}\left(\boldsymbol{D}^{\mathrm{H}}\left(\boldsymbol{\rho}^{\mathrm{mi}}\right)\right) \boldsymbol{U}=\boldsymbol{F}, \\ \quad \;\;\boldsymbol{D}^{\mathrm{H}}=\frac{1}{|Y|} \int_Y\left[\boldsymbol{D}(y)-\boldsymbol{D}(y) \boldsymbol{\varepsilon}_y(\boldsymbol{\phi}, y)\right] \mathrm{d} y, \\ \quad \;\;\sum\limits_{m=1}^{N^{\mathrm{mi}}} \bar{\tilde{\rho}}_m(i) v_m^{\mathrm{mi}}-\bar{V}^{\mathrm{mi}}=0, \\ \quad \;\;0 \leqslant \rho_m^{\mathrm{mi}} \leqslant 1 \quad\left(m=1, 2, \cdots, N^{\mathrm{mi}}\right), \end{array}\right. $$ (7) 其中，ρmi为微观设计变量，Nmi为微观设计域单元数目，微观体积约束上限为$ \bar{V}^{\mathrm{mi}}$. 为控制最小特征尺寸并获得清晰的黑白设计，本文采用Wang等[30]提出的鲁棒公式，过滤半径设为2.5. 采用改进的SIMP方法[31]对Di和$ \bar{\tilde{\boldsymbol{\rho}}}_i^{\mathrm{mi}}$进行插值:
$$ \boldsymbol{D}_i=\left(\underline{\rho}+(\bar{\rho}-\underline{\rho})\left(\bar{\tilde{\boldsymbol{\rho}}}_i^{\mathrm{mi}}\right)^p\right) \boldsymbol{D}_0, $$ (8) 其中，D0是材料的热传导系数矩阵，下标i表示微观设计域中的第i个单元. 为获得清晰的“0-1”设计，设置惩罚系数p>1(本文为p=3). 目标函数关于微观设计变量ρimi的导数可以写作
$$ \frac{\partial c}{\partial \rho_i^{\mathrm{mi}}}=-\sum\limits_e^{N^{\mathrm{ma}}} \boldsymbol{U}_e^{\mathrm{T}}\left(\int_{\varOmega_e} \boldsymbol{B}^{\mathrm{T}}\left(\frac{\partial \boldsymbol{D}^{\mathrm{H}}}{\partial \rho_i^{\mathrm{mi}}}\right) \boldsymbol{B} \mathrm{d} V\right) \boldsymbol{U}_e, $$ (9) 其中
$$ \frac{\partial \boldsymbol{D}^H}{\partial \bar{\tilde{\rho}}_i^{\mathrm{mi}}}=\frac{1}{|Y|} \int_Y\left[\boldsymbol{I}-\boldsymbol{\varepsilon}_y(\boldsymbol{\phi})\right]^{\mathrm{T}} \frac{\partial \boldsymbol{D}}{\partial \bar{\tilde{\rho}}_i^{\mathrm{mi}}}\left[\boldsymbol{I}-\boldsymbol{\varepsilon}_y(\boldsymbol{\phi})\right] \mathrm{d} Y, $$ (10) 且
$$ \frac{\partial \boldsymbol{D}}{\partial \bar{\tilde{\rho}}_i^{\mathrm{mi}}}=\left(p\left(\overline{\rho}-\underline{\rho}\right)\left(\bar{\tilde{\rho}}_i^{\mathrm{mi}}\right)^{p-1}\right) \boldsymbol{D}_0. $$ (11) 设置微观设计变量ρimi初始化后恰好满足体积约束$\bar{V}^{\mathrm{mi}} $. 微观设计域被离散为80×80个网格，为控制棋盘格现象，设置过滤半径rmin=2.5. 求解的优化求解器选取基于梯度的MMA算法，收敛准则为max‖xi+1－xi‖≤10－3，最大迭代步数设置为240.
3.2 微结构拓扑优化结果
1) 策略1：不考虑微结构之间的连通性
对体积分数分别为0.2，0.4，0.6，0.8的优化公式(7)求解，可以得到如图 5所示的4种微观结构. 本文将这些微观结构称为“基础微结构”.
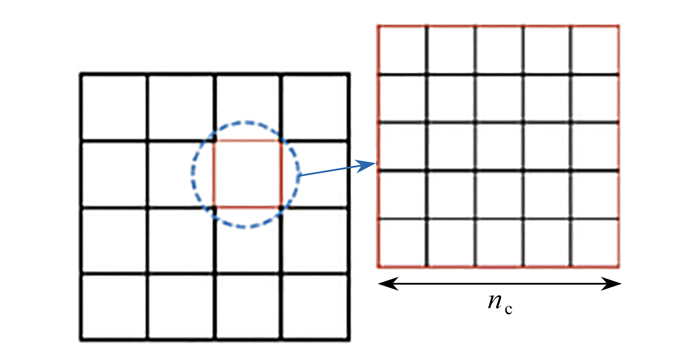
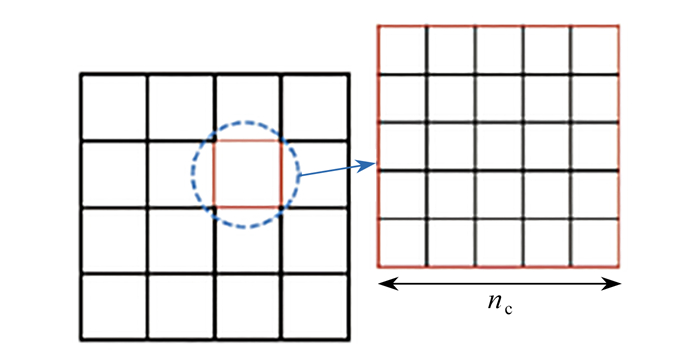
为保证经腐蚀和扩散后的微结构具有光滑边界，对微结构进行网格细化，将每个微观单元划分为nc×nc的细网格，如图 6所示. 本文选择nc=3，将微结构的网格细化为240×240.
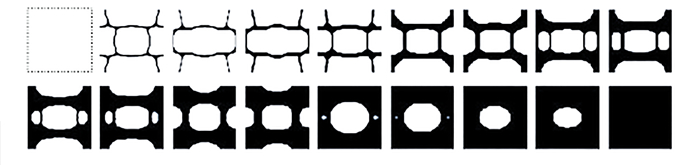
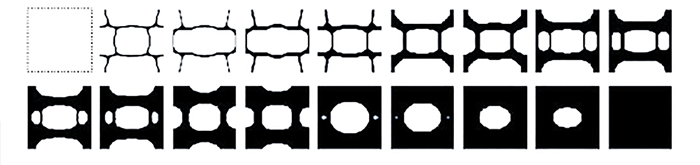
利用腐蚀-扩散算子，可以得到一系列密度从0至1变化的微结构，参数设置如下：过滤半径设为rmin=8.6，β值固定为128，微结构体积分数从0.05至1变化，间隔为0.05(共20步)，从而得到4×20个微结构，并选择若干体积分数均匀增大的微结构作为准周期微结构库①，用于后续的计算和优化，如图 7所示.
2) 策略2: 考虑微结构之间的连通性
由于策略1中不同体积分数的微结构拓扑是独立计算的，微结构间的连通性较差. 本文将体积分数较小的微结构作为不可设计域，依次优化获取体积分数较大的微结构. 首先，优化得到体积分数为0.2的微结构，并作为不可设计域优化体积分数为0.4的微结构，同理，优化得到体积分数为0.6和0.8的微结构. 从而得到4个连通性较好的基础微结构，如图 8所示. 应用策略1中的腐蚀-扩散算子，得到准周期微结构库②，如图 9所示.
4. 宏观尺度设计
4.1 等效材料属性
基于渐进均匀化法计算两组准周期微结构等效矩阵DH，
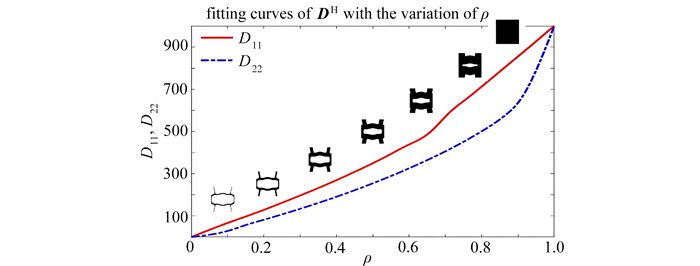
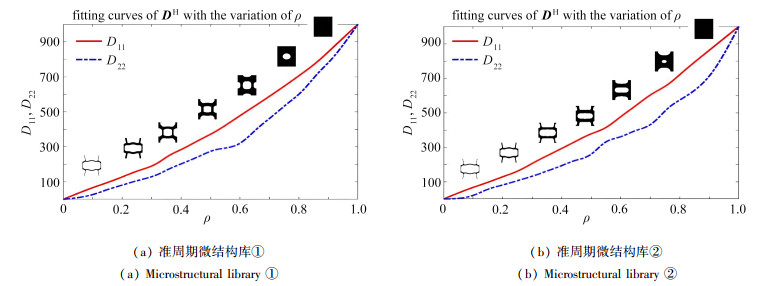
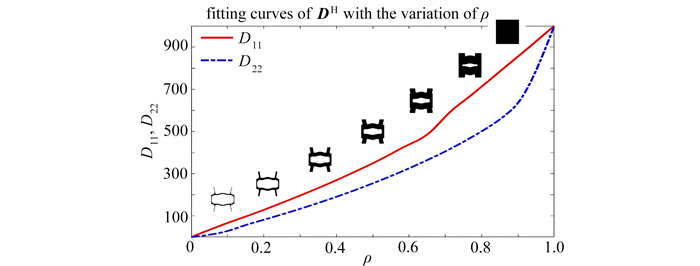
$$ \boldsymbol{D}^{\mathrm{H}}\left(\rho_e^{\mathrm{ma}}\right)=\boldsymbol{f}_{\text {spline }}\left(\rho_e^{\mathrm{ma}}\right), $$ (12) 并采用三次B-样条将其与设计变量ρema拟合，曲线如图 10所示.
4.2 宏观结构优化结果
将宏观密度ρema作为设计变量，其值对应准周期微结构库中密度相近的微结构. 优化公式可写成
$$ \left\{\begin{array}{l} \text {find} \quad \boldsymbol{\rho}^{\mathrm{ma}}, \\ \min \quad J \\ \quad\;\; \boldsymbol{K}\left(\boldsymbol{f}_{\text {spline }}\left(\boldsymbol{\rho}^{\mathrm{ma}}\right)\right) \boldsymbol{U}=\boldsymbol{F}, \\ \quad\;\; \sum\limits_{m=1}^{N^{\mathrm{ma}}} \bar{\tilde{\rho}}_m(i) v_m^{\mathrm{ma}}-\bar{V}^{\mathrm{ma}}=0, \\ \quad\;\;0 \leqslant \rho_m^{\mathrm{ma}} \leqslant 1 \quad\left(m=1, 2, \cdots, N^{\mathrm{ma}}\right), \end{array}\right. $$ (13) 其中，Nma为宏观设计域单元数目，体积约束上限为$ \bar{V}^{\text {ma }}$，密度过滤半径设为2.5.
结构热柔顺度关于宏观设计变量ρema的导数可以写作
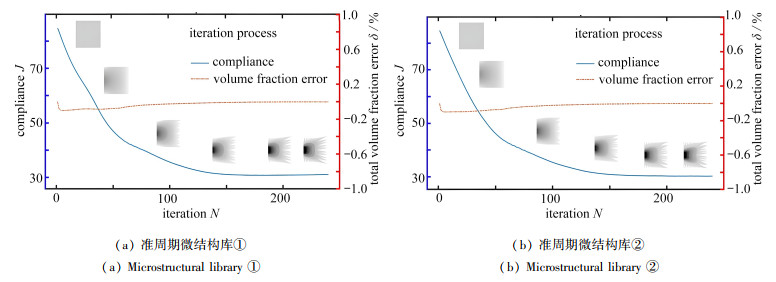
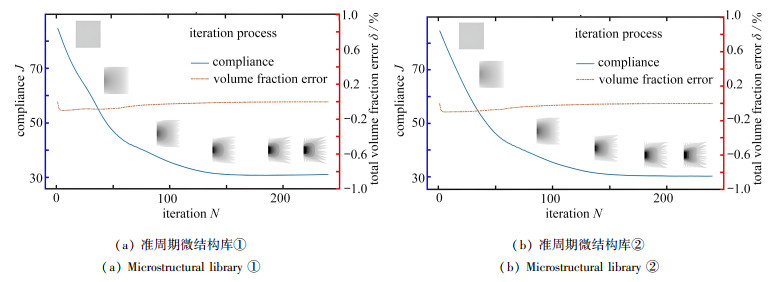
$$ \frac{\partial c}{\partial \rho_e^{\mathrm{ma}}}=-\boldsymbol{U}_e^{\mathrm{T}}\left(\int_{\varOmega_e} \boldsymbol{B}^{\mathrm{T}} \frac{\partial \boldsymbol{f}_{\text {spline }}\left(\rho_e^{\mathrm{ma}}, \rho_i^{\mathrm{mi}}\right)}{\partial \rho_e^{\mathrm{ma}}} \boldsymbol{B} \mathrm{d} V\right) \boldsymbol{U}_e, $$ (14) 其中，下标e=1, 2, ⋯, Nma. 迭代过程如图 11所示. 准周期微结构库①和准周期微结构库②的优化结构热柔顺度分别为31.279 3和30.252 6. 考虑连通性的结果值略小于不考虑连通性的结果值.
4.3 变密度胞元结构组装
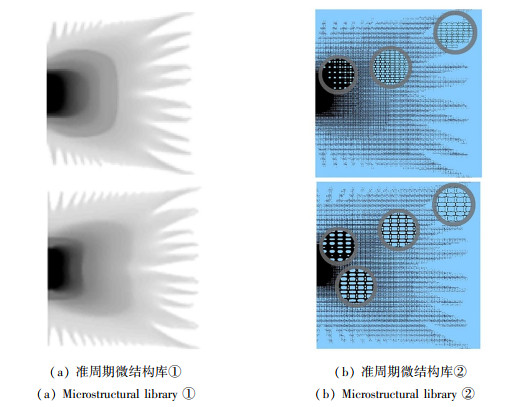
宏观优化完成后，利用体积分数最接近的微结构对各个宏观单元进行组装，得到变密度胞元结构，如图 12所示.
5. 比较与验证
在本节中，引入了另外两个方案验证方法的有效性. 方案一选择体积分数0.2的微结构拓扑优化结果作为唯一的基础微观结构，方案二为单一宏观尺度设计. 为了消除均匀化带来的误差，验证4种设计的性能，建立了4种设计的细网格模型，并计算了温度场.
5.1 两种对照方案
1) 单一基础微结构
方案一 选择体积分数为0.2的微结构作为单一基础微结构，经腐蚀、扩散，得到一个微结构族. 由于只有一个基础微结构，需要大的过滤半径来获得具有大体积分数的微结构，产生高额计算成本. 因此，我们调整了腐蚀-扩散策略：过滤半径设置为8.5，η=0.8和η=0.2分别实现腐蚀和扩散过程，从而得到两种微结构. 对新的微结构继续应用腐蚀-扩散，重复这个过程，建立准周期微结构库③，如图 13所示. 图 14为等效材料属性拟合曲线，图 15为宏观区域密度分布. 优化后结构的热柔顺度为31.393 1.
图 14 准周期微结构库③的等效热传导系数曲线Figure 14. Fitting curves of D11 and D22 with the variation of ρema in library ③2) 宏观单尺度设计
方案二 给出了宏观单尺度设计，以说明引入双尺度设计对结构性能的提升. 优化模型及参数与文献[32]相同. 拓扑优化结果如图 16所示，热柔顺度为48.162 9.
图 16 宏观单尺度拓扑优化结果Figure 16. The topology optimization result of the single macro-scale design5.2 方案验证
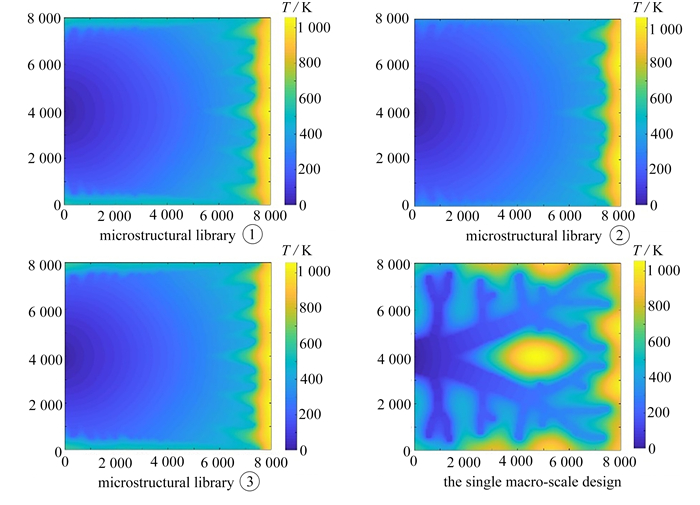
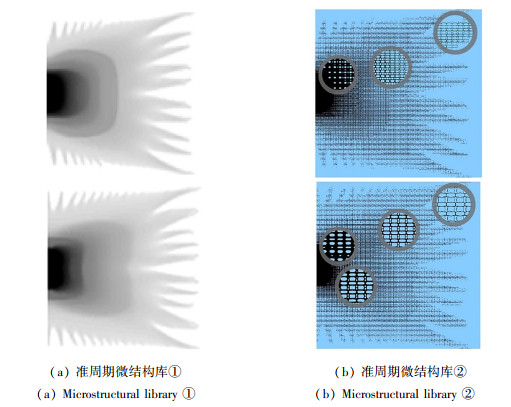
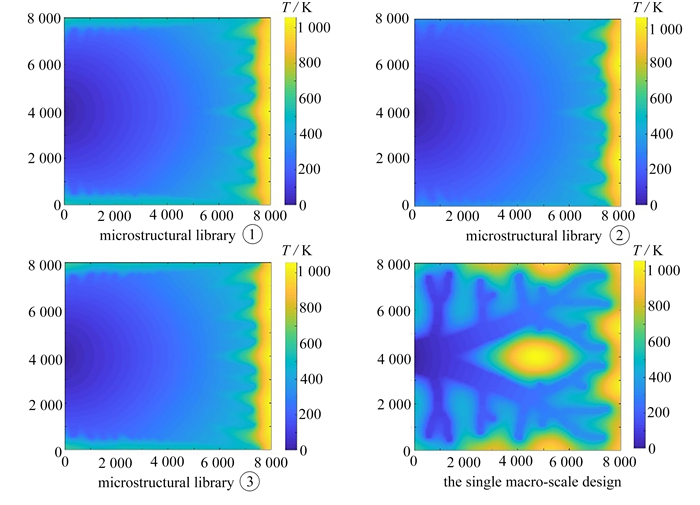
在拓扑优化过程中，采用渐近均匀化方法计算等效材料性质，并假定周期边界，忽略非均匀性和非连通性. 为了准确评定4种结果的散热性能，采用8 000×8 000的精细网格离散优化结果. 优化后结构的温度场如图 17所示. 计算温度场的一系列参数，用于后续对比，如表 1所示.
图 17 精细网格下的温度场优化结果Figure 17. Temperature fields of the 4 optimization results with the fine mesh表 1 不同策略优化结果的结构散热性能Table 1. Thermal performances of structures optimized by different strategiescompliance average temperature maximum temperature variance microstructural library ① 3.541 1E4 3.374 1E2 1.094 8E3 4.751 1E4 microstructural library ② 3.133 7E4 2.977 8E2 1.043 3E3 4.033 0E4 microstructural library ③ 3.303 3E4 3.126 1E2 1.001 9E3 4.125 8E4 the single macro-scale design 4.963 6E4 4.757 3E2 1.170 6E3 7.221 5E4 结果表明，变密度胞元结构比传统的宏观优化结构具有更好的热性能. 相比之下，其热柔顺度等参数明显降低. 在准周期微结构库①中，由于在微结构优化时没有加入不可设计域，导致一些微结构之间的连通性较弱，结构性能下降. 准周期微结构库③的构建只使用了体积分数为0.2的微结构，扩散得到体积分数较大的微结构与最佳微结构存在偏差，其散热性能也降低了. 此外，4种优化方案的最终结构体积分数分别为0.202 5，0.201 7，0.200 4和0.200 7. 体积分数偏差小，在允许范围内. 因此，本文提出的变密度多尺度拓扑优化方法是合理的，优化后的结构散热性能优异.
6. 结论
本文将变密度多尺度拓扑优化方法应用于散热结构优化. 基于腐蚀-扩散算子处理基础微结构生成准周期微结构库. 采用渐进均匀化方法计算微结构的等效热传导系数，得到拟合曲线，用于宏观优化，并组装变密度胞元结构. 此外，由于相邻微结构共享相似的微结构拓扑，具有较好的连通性. 数值算例表明，与传统的宏观尺度设计相比，变密度结构具有更好的散热性能.
-
图 1 变密度胞元结构及其几何参数与密度的关系
Figure 1. Illustration of the variable density cellular structure
图 3 提出算法的优化流程图
注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.
Figure 3. The optimization flowchart of the proposed method
图 14 准周期微结构库③的等效热传导系数曲线
Figure 14. Fitting curves of D11 and D22 with the variation of ρema in library ③
图 16 宏观单尺度拓扑优化结果
Figure 16. The topology optimization result of the single macro-scale design
图 17 精细网格下的温度场优化结果
Figure 17. Temperature fields of the 4 optimization results with the fine mesh
表 1 不同策略优化结果的结构散热性能
Table 1. Thermal performances of structures optimized by different strategies
compliance average temperature maximum temperature variance microstructural library ① 3.541 1E4 3.374 1E2 1.094 8E3 4.751 1E4 microstructural library ② 3.133 7E4 2.977 8E2 1.043 3E3 4.033 0E4 microstructural library ③ 3.303 3E4 3.126 1E2 1.001 9E3 4.125 8E4 the single macro-scale design 4.963 6E4 4.757 3E2 1.170 6E3 7.221 5E4 
下载: 导出CSV
-
[1] 彭世彬, 郭瑞, 冯上升, 等. 主动冷却点阵夹层防热结构温度响应计算模型[J]. 应用数学和力学, 2022, 43(5): 477-489. doi: 10.21656/1000-0887.420405PENG Shibin, GUO Rui, FENG Shangsheng, et al. A calculation model for temperature responses of active cooling lattice sandwich structures for thermal protection[J]. Applied Mathematics and Mechanics, 2022, 43(5): 477-489. (in Chinese) doi: 10.21656/1000-0887.420405 [2] ZHU J H, ZHANG W H, XIA L. Topology optimization in aircraft and aerospace structures design[J]. Archives of Computational Methods in Engineering, 2015, 23: 595-622. [3] LIU S, HU R, LI Q, et al. Topology optimization-based lightweight primary mirror design of a large-aperture space telescope[J]. Applied Optics, 2014, 53(35): 8318-8325. [4] 张东东, 栾福强, 赵礼辉, 等. 基于变体积约束的阻尼材料微结构拓扑优化研究[J]. 应用数学和力学, 2022, 43(6): 648-659. doi: 10.21656/1000-0887.420206ZHANG Dongdong, LUAN Fuqiang, ZHAO Lihui, et al. Research on topology optimization of damping material microstructures with varied volume constraints[J]. Applied Mathematics and Mechanics, 2022, 43(6): 648-659. (in Chinese) doi: 10.21656/1000-0887.420206 [5] RODRIGUES H, GUEDES J M, BENDSOE M P. Hierarchical optimization of material and structure[J]. Structural and Multidisciplinary Optimization, 2002, 24(1): 1-10. doi: 10.1007/s00158-002-0209-z [6] XIA L, BREITKOPF P. Concurrent topology optimization design of material and structure within FE2 nonlinear multiscale analysis framework[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 278: 524-542. doi: 10.1016/j.cma.2014.05.022 [7] XIA L, BREITKOPF P. Multiscale structural topology optimization with an approximate constitutive model for local material microstructure[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 286: 147-167. doi: 10.1016/j.cma.2014.12.018 [8] LIU L, YAN J, CHENG G. Optimum structure with homogeneous optimum truss-like material[J]. Computers & Structures, 2008, 86(13/14): 1417-1425. [9] YAN J, CHENG G D, LIU L. A uniform optimum material based model for concurrent optimization of thermoelastic structures and materials[J]. International Journal for Simulation and Multidisciplinary Design Optimization, 2008, 2(4): 259-266. doi: 10.1051/ijsmdo/2008035 [10] LONG K, WANG X, GU X. Concurrent topology optimization for minimization of total mass considering load-carrying capabilities and thermal insulation simultaneously[J]. Acta Mechanica Sinica, 2018, 34(2): 315-326. doi: 10.1007/s10409-017-0708-1 [11] YAN X, HUANG X, SUN G, et al. Two-scale optimal design of structures with thermal insulation materials[J]. Composite Structures, 2015, 120: 358-365. doi: 10.1016/j.compstruct.2014.10.013 [12] YAN J, GUO X, CHENG G. Multi-scale concurrent material and structural design under mechanical and thermal loads[J]. Computational Mechanics, 2016, 57(3): 437-446. doi: 10.1007/s00466-015-1255-x [13] ZHANG P, TOMAN J, YU Y, et al. Efficient design-optimization of variable-density hexagonal cellular structure by additive manufacturing: theory and validation[J]. Journal of Manufacturing Science & Engineering, 2015, 137(2): 021004-021013. [14] WANG B, CHENG G. Design of cellular structures for optimum efficiency of heat dissipation[J]. Structural and Multidisciplinary Optimization, 2005, 30(6): 447-458. doi: 10.1007/s00158-005-0542-0 [15] CHENG L, LIU J, LIANG X, et al. Coupling lattice structure topology optimization with design-dependent feature evolution for additive manufactured heat conduction design[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 332: 408-439. doi: 10.1016/j.cma.2017.12.024 [16] CHENG L, LIU J, TO A C. Concurrent lattice infill with feature evolution optimization for additive manufactured heat conduction design[J]. Structural and Multidisciplinary Optimization, 2018, 58(2): 511-535. doi: 10.1007/s00158-018-1905-7 [17] WU Z, XIA L, WANG S, et al. Topology optimization of hierarchical lattice structures with substructuring[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 345: 602-617. doi: 10.1016/j.cma.2018.11.003 [18] WANG Y, CHEN F, WANG M Y. Concurrent design with connectable graded microstructures[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 317: 84-101. doi: 10.1016/j.cma.2016.12.007 [19] WANG Y, ZHANG L, DAYNES S, et al. Design of graded lattice structure with optimized mesostructures for additive manufacturing[J]. Materials & Design, 2018, 142: 114-123. [20] ZONG H, LIU H, MA Q, et al. VCUT level set method for topology optimization of functionally graded cellular structures[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 354: 487-505. doi: 10.1016/j.cma.2019.05.029 [21] ZHANG Y, LI H, XIAO M, et al. Concurrent topology optimization for cellular structures with nonuniform microstructures based on the Kriging metamodel[J]. Structural and Multidisciplinary Optimization, 2019, 59(4): 1273-1299. doi: 10.1007/s00158-018-2130-0 [22] ZHANG Y, XIAO M, GAO L, et al. Multiscale topology optimization for minimizing frequency responses of cellular composites with connectable graded microstructures[J]. Mechanical Systems and Signal Processing, 2020, 135: 106369. doi: 10.1016/j.ymssp.2019.106369 [23] SIGMUND O. Tailoring materials with prescribed elastic properties[J]. Mechanics of Materials, 1995, 20(4): 351-368. doi: 10.1016/0167-6636(94)00069-7 [24] OSANOV M, GUEST J K. Topology optimization for architected materials design[J]. Annual Review of Materials Research, 2016, 46(1): 211-233. doi: 10.1146/annurev-matsci-070115-031826 [25] CHEN W, LIU S. Topology optimization of microstructures of viscoelastic damping materials for a prescribed shear modulus[J]. Structural and Multidisciplinary Optimization, 2014, 50(2): 287-296. doi: 10.1007/s00158-014-1049-3 [26] WANG Y, WANG M Y, CHEN F. Structure-material integrated design by level sets[J]. Structural and Multidisciplinary Optimization, 2016, 54(5): 1145-1156. doi: 10.1007/s00158-016-1430-5 [27] 杨航, 马力. 多材料点阵结构的热可编程力学行为[J]. 应用数学和力学, 2022, 43(5): 534-552. doi: 10.21656/1000-0887.430104YANG Hang, MA Li. Multimaterial lattice structures with thermally programmable mechanical behaviors[J]. Applied Mathematics and Mechanics, 2022, 43(5): 534-552. (in Chinese) doi: 10.21656/1000-0887.430104 [28] BOURDIN B. Filters in topology optimization[J]. International Journal for Numerical Methods in Engineering, 2001, 50(9): 2143-2158. doi: 10.1002/nme.116 [29] PAPANICOLAU G, BENSOUSSAN A, LIONS J L. Asymptotic Analysis for Periodic Structures[M]. Elsevier, 1978. [30] WANG F, LAZAROV B S, SIGMUND O. On projection methods, convergence and robust formulations in topology optimization[J]. Structural and Multidisciplinary Optimization, 2011, 43(6): 767-784. doi: 10.1007/s00158-010-0602-y [31] BENDSØE M P, SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9/10): 635-654. [32] SIGMUND O. Morphology-based black and white filters for topology optimization[J]. Structural and Multidisciplinary Optimization, 2007, 33(4/5): 401-424. 期刊类型引用(0)
其他类型引用(1)
-
下载:
计量
- 文章访问数: 560
- HTML全文浏览量: 209
- PDF下载量: 64
- 被引次数: 1
渝公网安备50010802005915号