基于降阶模型和数据驱动的动态结构数字孪生方法

王青山; 严波; 陈岩; 邓茂; 蔡源斌

doi:10.21656/1000-0887.430384

基于降阶模型和数据驱动的动态结构数字孪生方法

doi: 10.21656/1000-0887.430384

重庆大学航空航天学院，重庆 400044

(我刊编委严波来稿)

基金项目:

国家自然科学基金项目 11572060

详细信息

作者简介:
王青山(1997—)，男，硕士生(E-mail: wqs20166229@163.com)

通讯作者:
严波(1965—)，男，教授，博士，博士生导师(通讯作者. E-mail: boyan@cqu.edu.cn)

中图分类号: O32
计量
- 文章访问数: 963
- HTML全文浏览量: 266
- PDF下载量: 245
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-29
- 修回日期: 2022-12-09
- 刊出日期: 2023-07-01

Digital Twin Method for Dynamic Structures Based on Reduced Order Models and Data Driving

College of Aerospace Engineering, Chongqing University, Chongqing 400044, P.R.China

(Contributed by YAN Bo, M.AMM Editorial Board)

摘要

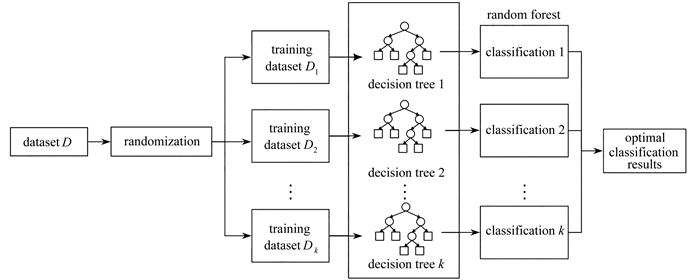
摘要: 针对受动载荷作用的结构，提出了一种基于降阶模型库和机器学习数据驱动的数字孪生构建方法. 首先根据物理结构服役过程中可能出现的损伤状态，采用有限单元法建立高保真有限元模型. 其次采用Krylov子空间模型降阶方法对模型进行降阶，建立了物理结构各种状态下的降阶模型，形成模型库. 最后利用随机森林机器学习算法训练获得模型选择器，通过物理结构上传感器的数据推断当前物理结构的状态，驱动数字孪生体跟随物理结构一同演化. 设计制作了一个框架结构物理模型，模拟了结构不同位置损伤及不同损伤程度，验证了提出的数字孪生构建方法.
- 结构数字孪生 /
- 降阶模型库 /
- Krylov子空间模型降阶 /
- 随机森林 /
- 数据驱动
Abstract: A digital twin construction method based on the reduced order model library and machine learning was proposed for structures under dynamic loads. Firstly, the high-fidelity finite element models were established according to the possible damage states occurring during the service of the physical structures. Secondly, the Krylov subspace order reduction method was used to reduce the orders of the models and the reduced order models were assembled to a library. Finally, the random forest machine learning algorithm was used to train the model selector, infer the current state of the physical structure through the sensor data from the structure, and then drive the digital twin to evolve with the physical structure. A physical frame structure was designed and manufactured to simulate the damages of different degrees at different points, and verify the proposed digital twin construction method for dynamic structures.
- structural digital twin /
- reduced order model library /
- Krylov subspace model order reduction /
- random forest /
- data-driven method
edited-by

edited-by
注释:

1) (我刊编委严波来稿)

HTML全文

图 1 随机森林算法示意图

Figure 1. The flowchart of the random forest algorithm

下载: 全尺寸图片幻灯片

图 2 物理结构与数字孪生体

注为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.

Figure 2. The physical structure and the digital twin

下载: 全尺寸图片幻灯片

图 3 空间框架结构示意图

Figure 3. Schematic diagram of the frame structure

下载: 全尺寸图片幻灯片

图 4 框架结构物理实体及测试系统

Figure 4. The physical frame structure and the test system

下载: 全尺寸图片幻灯片

图 5 框架结构模型库

Figure 5. The model library of the framework structure

下载: 全尺寸图片幻灯片

图 6 模型选择器测试数据混淆矩阵

Figure 6. The confusion matrix of the testing sample

下载: 全尺寸图片幻灯片

图 7 结构实测与数字孪生预测结果比较

Figure 7. Comparison of measured values and predicted results by digital twin

下载: 全尺寸图片幻灯片

图 8 框架结构数字孪生体给出的典型时刻的应变分布

Figure 8. Strain distributions at typical moments predicted by the digital twin of the frame structure

下载: 全尺寸图片幻灯片

图 9 位置2损伤演变过程中数字孪生体的更新

Figure 9. Update of the digital twin during evolution of damage at point 2

下载: 全尺寸图片幻灯片

参考文献(29)

[1]	GRIEVES M, VICKERS J. Digital twin: mitigating unpredictable, undesirable emergent behavior in complex systems[M]//Transdisciplinary Perspectives on Complex Systems. Springer, 2017: 85-113.
[2]	TAO F, XIAO B, QI Q, et al. Digital twin modeling[J]. Journal of Manufacturing Systems, 2022, 64: 372-389. doi: 10.1016/j.jmsy.2022.06.015
[3]	董雷霆, 周轩, 赵福斌, 等. 飞机结构数字孪生关键建模仿真技术[J]. 航空学报, 2021, 42(3): 113-141. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202103012.htm DONG Leiting, ZHOU Xuan, ZHAO Fubin, et al. Key modeling and simulation technology of aircraft structure digital twin[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(3): 113-141. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202103012.htm
[4]	HAAG S, ANDERL R. Digital twin-proof of concept[J]. Manufacturing Letters, 2018, 15(B): 64-66.
[5]	MOI T, CIBICIK A, RØLVÅG T. Digital twin based condition monitoring of a knuckle boom crane: an experimental study[J]. Engineering Failure Analysis, 2020, 112(3): 104517.
[6]	WANG S, LAI X, HE X, et al. Building a trustworthy product-level shape-performance integrated digital twin with multifidelity surrogate model[J]. Journal of Mechanical Design, 2022, 144(3): 031703-0317114. doi: 10.1115/1.4052390
[7]	LAI X, HE X, WANG S, et al. Building a lightweight digital twin of a crane boom for structural safety monitoring based on a multifidelity surrogate model[J]. Journal of Mechanical Design, 2022, 144(6): 064502. doi: 10.1115/1.4053606
[8]	KAPTEYN M G, KNEZEVIC D J, HUYNH D, et al. Data-driven physics-based digital twins via a library of component-based reduced-order models[J]. International Journal for Numerical Methods in Engineering, 2022, 123(13): 2986-3003. doi: 10.1002/nme.6423
[9]	KAPTEYN M G, KNEZEVIC D J, WILLCOX K. Toward predictive digital twins via component-based reduced-order models and interpretable machine learning[C]//Proceedings of the AIAA Scitech 2020 Forum. Orlando, 2020.
[10]	MILANOSKI D P, GALANOPOULOS G K, LOUTAS T H. Digital-twins of composite aerostructures towards structural health monitoring[C]// 2021 IEEE 8th International Workshop on Metrology for AeroSpace (MetroAeroSpace). Naples, Italy, 2021.
[11]	WANG J, YE L, GAO R X, et al. Digital twin for rotating machinery fault diagnosis in smart manufacturing[J]. International Journal of Production Research, 2019, 57(12): 3920-3934. doi: 10.1080/00207543.2018.1552032
[12]	GANGULI R, ADHIKARI S. The digital twin of discrete dynamic systems: initial approaches and future challenges[J]. Applied Mathematical Modelling, 2020, 77(2): 1110-1128.
[13]	CHAKRABORTY S, ADHIKARI S. Machine learning based digital twin for dynamical systems with multiple time-scales[J]. Computers & Structures, 2021, 243: 106410.
[14]	赖学方, 王晓龙, 聂玉峰. 基于Mori-Zwanzig格式和偏最小二乘的非线性模型降阶[J]. 应用数学和力学, 2021, 42(6): 551-561. doi: 10.21656/1000-0887.410230 LAI Xuefang, WANG Xiaolong, NIE Yufeng. Nonlinear model reduction based on Mori-Zwanzig scheme and partial least squares[J]. Applied Mathematics and Mechanics, 2021, 42(6): 551-561. (in Chinese) doi: 10.21656/1000-0887.410230
[15]	罗振东, 张博. Sobolev方程基于POD的降阶外推差分算法[J]. 应用数学和力学, 2016, 37(1): 107-116. doi: 10.3879/j.issn.1000-0887.2016.01.009 LUO Zhendong, ZHANG Bo. Reduced order extrapolation difference algorithm based on pod for Sobolev equation[J]. Applied Mathematics and Mechanics, 2016, 37(1): 107-116. (in Chinese) doi: 10.3879/j.issn.1000-0887.2016.01.009
[16]	PATERA A T, ROZZA G. Reduced Basis Approximation and a Posteriori Error Estimation for Parametrized Partial Differential Equations[M]. Massachusetts Institute of Technology, 2007.
[17]	QUARTERONI A, MANZONI A, NEGRI F. Reduced Basis Methods for Partial Differential Equations: an Introduction[M]. Springer, 2015.
[18]	VALLAGHÉ S, HUYNH P, KNEZEVIC D J, et al. Component-based reduced basis for parametrized symmetric eigenproblems[J]. Advanced Modeling and Simulation in Engineering Sciences, 2015, 2(1): 1-30. doi: 10.1186/s40323-014-0017-1
[19]	张珺, 李立州, 原梅妮. 径向基函数参数化翼型的气动力降阶模型优化[J]. 应用数学和力学, 2019, 40(3): 250-258. doi: 10.21656/1000-0887.390187 ZHANG Jun, LI Lizhou, YUAN Meini. Aerodynamic model optimization for radial basis function parameterized airfoils[J]. Applied Mathematics and Mechanics, 2019, 40(3): 250-258. (in Chinese) doi: 10.21656/1000-0887.390187
[20]	GUGERCIN S, ANTOULAS A C. A survey of model reduction by balanced truncation and some new results[J]. International Journal of Control, 2004, 77(8): 748-766. doi: 10.1080/00207170410001713448
[21]	KVRSCHNER P. Balanced truncation model order reduction in limited time intervals for large systems[J]. Advances in Computational Mathematics, 2018, 44(6): 1821-1844. doi: 10.1007/s10444-018-9608-6
[22]	GUYAN R J. Reduction of stiffness and mass matrices[J]. AIAA Journal, 1965, 3(2): 380. doi: 10.2514/3.2874
[23]	BAI Z. Krylov subspace techniques for reduced-order modeling of large-scale dynamical systems[J]. Applied Numerical Mathematics, 2002, 43(1/2): 9-44.
[24]	BEATTIE C, GUGERCIN S. Model reduction by rational interpolation[M]//Model Reduction and Approximation. Society for Industrial and Applied Mathematics, 2017: 297-334.
[25]	SALIMBAHRAMI B, LOHMANN B. Order reduction of large scale second-order systems using Krylov subspace methods[J]. Linear Algebra and Its Applications, 2006, 415(2/3): 385-405.
[26]	ARNOLDI W E. The principle of minimized iterations in the solution of the matrix eigenvalue problem[J]. Quarterly of Applied Mathematics, 1951, 9(1): 17-29.
[27]	BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32.
[28]	严波. 有限单元法基础[M]. 北京: 高等教育出版社, 2022: 396-397. YAN Bo. Foundation of Finite Element Method[M]. Beijing: Higher Education Press, 2022: 396-397. (in Chinese)
[29]	ADHIKARI S, BHATTACHARYA S. Dynamic analysis of wind turbine towers on flexible foundations[J]. Shock and Vibration, 2012, 19(1): 37-56.