矩形边界越流承压含水层中非完整井稳定流解析解

孙前林; 谭卫佳; 徐蓓艺; 王旭东

doi:10.21656/1000-0887.430398

矩形边界越流承压含水层中非完整井稳定流解析解

doi: 10.21656/1000-0887.430398

南京工业大学岩土工程研究所，南京 211816

基金项目:

国家自然科学基金青年科学基金项目 41807189

详细信息

作者简介:
孙前林(1997—)，男，硕士生(E-mail: 202061225023@njtech.edu.cn)

通讯作者:
王旭东(1963—)，男，教授(通讯作者. E-mail: cewxd@njtech.edu.cn)

中图分类号: TU470
计量
- 文章访问数: 435
- HTML全文浏览量: 137
- PDF下载量: 56
- 被引次数: 0
出版历程
- 收稿日期: 2022-12-21
- 修回日期: 2023-05-06
- 刊出日期: 2023-08-01

Analytical Solutions of Steady Flow Toward a Partially Penetrating Well in a Rectangular Leaky-Confined Aquifer

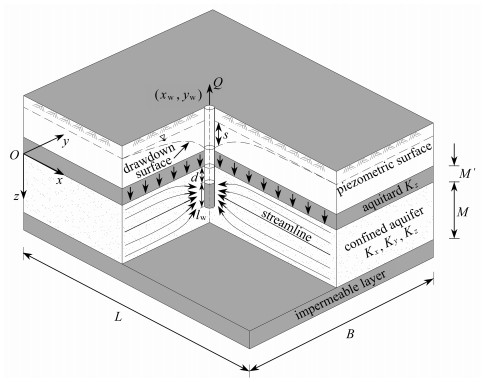
Institute of Geotechnical Engineering, Nanjing Tech University, Nanjing 211816, P.R.China

摘要

摘要: 针对矩形边界越流承压含水层中非完整井抽水引起的复杂地下水流动问题，建立了直角坐标系下越流承压含水层非完整井稳定流数学模型. 通过对地下水流动计算模型的有限Fourier变换和有限Fourier变换域降深函数的逆变换，提出了不同类型边界条件下越流承压含水层非完整井三维稳定流降深解析解. 在验证降深解析解正确性的基础上，通过降深解析解计算精度的分析，并结合非完整井抽水条件下含水层地下水流动特性，给出了降深解析解满足计算精度要求的计算项数取值. 探讨了含水层正交各向异性、抽水井完整性、井位布置等因素对含水层降深和地下水流动的影响规律，并利用工程案例阐明了降深解析解的工程适用性.
- 矩形边界承压含水层 /
- 非完整井 /
- 三维稳定流 /
- 直角坐标系 /
- 解析解
Abstract: For the complicated problem of groundwater flow to a partially penetrating well in a rectangular confined aquifer, a mathematical model describing the groundwater flow to a partially penetrating well pumped at a constant rate in a rectangular leaky-confined aquifer, was established. The analytical solutions of the 3D steady flow in the Cartesian coordinate system under different boundary conditions, were derived through the finite Fourier transform and the inverse transform. After the verification of the analytical solution of drawdown, the number of calculation items satisfying the calculation accuracy requirement was given, based on the analysis of the calculation accuracy of the analytical solution and the characteristics of the groundwater flow to a partially penetrating well. Moreover, the effects of orthotropy, well integrity and well location on the drawdown and seepage fields, were discussed. The engineering examples demonstrate the applicability of the proposed analytical method.
- rectangular confined aquifer /
- partially penetrating well /
- 3D steady flow /
- Cartesian coordinate system /
- analytical solution

HTML全文

图 1 矩形边界越流承压含水层非完整井计算模型

Figure 1. The calculation model for the partially penetrating well in a rectangular leaky-confined aquifer

下载: 全尺寸图片幻灯片

图 2 降深分布曲线(越流与无越流)

Figure 2. Drawdown distribution curves(leakage and non-leakage)

下载: 全尺寸图片幻灯片

图 3 降深分布曲线(完整井与非完整井)

Figure 3. Drawdown distribution curves(fully penetrating well and partially penetrating well)

下载: 全尺寸图片幻灯片

图 4 降深及相对误差随计算项数的变化(完整井)

Figure 4. Variations of drawdowns and relative errors with the number of calculation items (fully penetrating well)

下载: 全尺寸图片幻灯片

图 5 降深及相对误差随计算项数的变化(非完整井)

Figure 5. Variations of drawdowns and relative errors with the number of calculation items (partially penetrating well)

下载: 全尺寸图片幻灯片

图 6 降深分布曲线

Figure 6. Drawdown distribution curves

下载: 全尺寸图片幻灯片

图 7 承压含水层非完整井水力梯度(剖面)

Figure 7. Gradients of the partially penetrating well in a confined aquifer(profile)

下载: 全尺寸图片幻灯片

图 8 降深等值线及水力梯度(平面)

Figure 8. Drawdown contours and gradients(plane)

下载: 全尺寸图片幻灯片

图 9 抽水井和观测井布置(单位: m)

Figure 9. The pumping well and the observation well layout(unit: m)

下载: 全尺寸图片幻灯片

图 10 地下水计算模型(单位: m)

Figure 10. The groundwater calculation model(unit: m)

下载: 全尺寸图片幻灯片

图 11 降深计算值与实测值对比

Figure 11. Comparison of calculated and measured values of the drawdown

下载: 全尺寸图片幻灯片

B1 不同类型边界条件下的特征函数、特征值、范数以及变换参数

B1. Characteristic functions, eigenvalues, norms and transformation parameters under different boundary conditions

coordinate axis	boundary condition	eigenvalue	characteristic function	norm	transformation parameter
x	$\left.s\right\|_{x=0}=\left.s\right\|_{x=L}=0$	$\alpha_m=\frac{m {\rm{ \mathsf{π} }} }{L}$	$\varphi_m\left(\alpha_m x\right)=\sin \left(\alpha_m x\right)$	$M\left(\alpha_m\right)=\frac{L}{2}(m \geqslant 1)$	$m \in[1, \infty)$
x	$\left.\frac{\partial s}{\partial x}\right\|_{x=0}=\left.s\right\|_{x=L}=0$	$\alpha_m=\frac{(2 m+1) {\rm{ \mathsf{π} }} }{2 L}$	$\varphi_m\left(\alpha_m x\right)=\cos \left(\alpha_m x\right)$	$M\left(\alpha_m\right)=\frac{L}{2}(m \geqslant 0)$	$m \in[0, \infty)$
y	$\left.s\right\|_{y=0}=\left.s\right\|_{y=B}=0$	$\beta_n=\frac{n {\rm{ \mathsf{π} }} }{B}$	$\psi_n\left(\beta_n y\right)=\sin \left(\beta_n y\right)$	$N\left(\beta_n\right)=\frac{B}{2}(n \geqslant 1)$	$n \in[1, \infty)$
	$\left.\frac{\partial s}{\partial y}\right\|_{y=0}=\left.\frac{\partial s}{\partial y}\right\|_{y=B}=0$	$\beta_n=\frac{n {\rm{ \mathsf{π} }} }{B}$	$\psi_n\left(\beta_n y\right)=\cos \left(\beta_n y\right)$	$N\left(\beta_n\right)=\left\{\begin{array}{l} B(n=0) \\ B / 2(n \geqslant 1) \end{array}\right.$	$n \in[0, \infty)$
	$\left.\frac{\partial s}{\partial y}\right\|_{y=0}=\left.s\right\|_{y=B}=0$	$\beta_n=\frac{(2 n+1) {\rm{ \mathsf{π} }} }{2 B}$	$\psi_n\left(\beta_n y\right)=\cos \left(\beta_n y\right)$	$N\left(\beta_n\right)=\frac{B}{2}(n \geqslant 0)$	$n \in[0, \infty)$
z	$\left.\frac{\partial s}{\partial z}\right\|_{z=0}=\left.\frac{\partial s}{\partial z}\right\|_{z=M}=0$	$\lambda_k=\frac{k {\rm{ \mathsf{π} }} }{M}$	$\chi_k\left(\lambda_k z\right)=\cos \left(\lambda_k z\right)$	$K\left(\lambda_k\right)=\left\{\begin{array}{l} M(k=0) \\ M / 2(k \geqslant 1) \end{array}\right.$	$k \in[0, \infty)$

下载: 导出CSV

C1 降深解析解(case 1~3)

C1. Analytic solutions of the drawdown(case 1~3)

case	boundary condition	schematic plan	s(x, y, z)
1	4 fixed-head boundary		$\begin{aligned} s= & \frac{4 Q}{B L M}\left[\sum_{n=1}^{\infty} \sum_{m=1}^{\infty} \frac{\theta_{m n}}{\beta_{m n}^2} \sin \left(\frac{m {\rm{ \mathsf{π} }} x}{L}\right) \sin \left(\frac{n {\rm{ \mathsf{π} }} y}{B}\right)+\right. \\ & \left.2 \sum_{k=1}^{\infty} \sum_{n=1}^{\infty} \sum_{m=1}^{\infty} \frac{\xi_k \theta_{m n}}{\beta_{m n k}^2} \sin \left(\frac{m {\rm{ \mathsf{π} }} x}{L}\right) \sin \left(\frac{n {\rm{ \mathsf{π} }} y}{B}\right) \cos \left(\frac{k {\rm{ \mathsf{π} }} z}{M}\right)\right] \end{aligned}$
1	4 fixed-head boundary		$\theta_{m n}=\sin \left(\frac{m {\rm{ \mathsf{π} }} x_{\mathrm{w}}}{L}\right) \sin \left(\frac{n {\rm{ \mathsf{π} }} y_{\mathrm{w}}}{B}\right)$
2	4 impermeable boundary		$\begin{aligned} s= & \frac{Q}{B L M}\left[\sum_{n=0}^{\infty} \sum_{m=0}^{\infty} \varepsilon_{m n} \frac{\theta_{m n}}{\beta_{m n}^2} \cos \left(\frac{m {\rm{ \mathsf{π} }} x}{L}\right) \cos \left(\frac{n {\rm{ \mathsf{π} }} y}{B}\right)+\right. \\ & \left.2 \sum_{k=1}^{\infty} \sum_{n=0}^{\infty} \sum_{m=0}^{\infty} \varepsilon_{m n} \frac{\xi_k \theta_{m n}}{\beta_{m n k}^2} \cos \left(\frac{m {\rm{ \mathsf{π} }} x}{L}\right) \cos \left(\frac{n {\rm{ \mathsf{π} }} y}{B}\right) \cos \left(\frac{k {\rm{ \mathsf{π} }} z}{M}\right)\right] \end{aligned}$
			$\theta_{m n}=\cos \left(\frac{m {\rm{ \mathsf{π} }} x_{\mathrm{w}}}{L}\right) \cos \left(\frac{n {\rm{ \mathsf{π} }} y_{\mathrm{w}}}{B}\right)$
			$\varepsilon_{m n}= \begin{cases}1, & m=0, n=0, \\ 2, & m=0, n \geqslant 1 \quad \text { or } \quad m \geqslant 1, n=0, \\ 4, \quad & m \geqslant 1, n \geqslant 1\end{cases}$
3	2 fixed-head boundary (parallel) 2 impermeable boundary		$\begin{aligned} s= & \frac{2 Q}{B L M}\left[\sum_{n=0}^{\infty} \sum_{m=1}^{\infty} \varepsilon_n \frac{\theta_{m n}}{\beta_{m n}^2} \sin \left(\frac{m {\rm{ \mathsf{π} }} x}{L}\right) \cos \left(\frac{n {\rm{ \mathsf{π} }} y}{B}\right)+\right. \\ & \left.2 \sum_{k=1}^{\infty} \sum_{n=0}^{\infty} \sum_{m=1}^{\infty} \varepsilon_n \frac{\xi_k \theta_{m n}}{\beta_{m n k}^2} \sin \left(\frac{m {\rm{ \mathsf{π} }} x}{L}\right) \cos \left(\frac{n {\rm{ \mathsf{π} }} y}{B}\right) \cos \left(\frac{k {\rm{ \mathsf{π} }} z}{M}\right)\right] \end{aligned}$
			$\theta_{m n}=\sin \left(\frac{m {\rm{ \mathsf{π} }} x_{\mathrm{w}}}{L}\right) \cos \left(\frac{n {\rm{ \mathsf{π} }} y_{\mathrm{w}}}{B}\right)$
			$\varepsilon_n= \begin{cases}1, & n=0, \\ 2, & n \geqslant 1\end{cases}$
$\beta_{m n k}^2=K_x\left(\frac{m {\rm{ \mathsf{π} }} }{L}\right)^2+K_y\left(\frac{n {\rm{ \mathsf{π} }} }{B}\right)^2+K_z\left(\frac{k {\rm{ \mathsf{π} }} }{M}\right)^2+\frac{K_z^{\prime}}{M M^{\prime}}, \beta_{m n}^2=K_x\left(\frac{m {\rm{ \mathsf{π} }} }{L}\right)^2+K_y\left(\frac{n {\rm{ \mathsf{π} }} }{B}\right)^2+\frac{K_z^{\prime}}{M M^{\prime}}$

下载: 导出CSV

C2 降深解析解(case 4)

C2. Analytic solutions of the drawdown(case 4)

case	boundary condition	schematic plan	s(x, y, z)
4	2 fixed-head boundary 2 impermeable boundary		$\begin{aligned} s= & \frac{4 Q}{B L M}\left[\sum_{n=0}^{\infty} \sum_{m=0}^{\infty} \frac{\theta_{m n}}{\beta_{m n}^2} \cos \left(\frac{(2 m+1) {\rm{ \mathsf{π} }} x}{2 L}\right) \cos \left(\frac{(2 n+1) {\rm{ \mathsf{π} }} y}{2 B}\right)+\right. \\ & \left.2 \sum_{k=1}^{\infty} \sum_{n=0}^{\infty} \sum_{m=0}^{\infty} \frac{\xi_k \theta_{m n}}{\beta_{m n k}^2} \cos \left(\frac{(2 m+1) {\rm{ \mathsf{π} }} x}{2 L}\right) \cos \left(\frac{(2 n+1) {\rm{ \mathsf{π} }} y}{2 B}\right) \cos \left(\frac{k {\rm{ \mathsf{π} }} z}{M}\right)\right] \end{aligned}$
4	2 fixed-head boundary 2 impermeable boundary		$\theta_{m n}=\cos \left(\frac{(2 m+1) {\rm{ \mathsf{π} }} x_{\mathrm{w}}}{2 L}\right) \cos \left(\frac{(2 n+1) {\rm{ \mathsf{π} }} y_{\mathrm{w}}}{2 B}\right)$
$\beta_{m n k}^2=K_x\left(\frac{(2 m+1) {\rm{ \mathsf{π} }} }{2 L}\right)^2+K_y\left(\frac{(2 n+1) {\rm{ \mathsf{π} }} }{2 B}\right)^2+K_z\left(\frac{k {\rm{ \mathsf{π} }} }{M}\right)^2+\frac{K_z^{\prime}}{M M^{\prime}}, \beta_{m n}^2=K_x\left(\frac{(2 m+1) {\rm{ \mathsf{π} }} }{2 L}\right)^2+K_y\left(\frac{(2 n+1) {\rm{ \mathsf{π} }} }{2 B}\right)^2+\frac{K_z^{\prime}}{M M^{\prime}}$

下载: 导出CSV

C3 降深解析解(case 5, 6)

C3. C3 Analytic solutions of the drawdown(case 5, 6)

case	boundary condition	schematic plan	s(x, y, z)
5	1 fixed-head boundary 3 impermeable boundary		$\begin{aligned} s= & \frac{2 Q}{B L M}\left[\sum_{n=0}^{\infty} \sum_{m=0}^{\infty} \varepsilon_n \frac{\theta_{m n}}{\beta_{m n}^2} \cos \left(\frac{(2 m+1) {\rm{ \mathsf{π} }} x}{2 L}\right) \cos \left(\frac{n {\rm{ \mathsf{π} }} y}{B}\right)+\right. \\ & \left.2 \sum_{k=1}^{\infty} \sum_{n=0}^{\infty} \sum_{m=0}^{\infty} \varepsilon_n \frac{\xi_k \theta_{m n}}{\beta_{m n k}^2} \cos \left(\frac{(2 m+1) {\rm{ \mathsf{π} }} x}{2 L}\right) \cos \left(\frac{n {\rm{ \mathsf{π} }} y}{B}\right) \cos \left(\frac{k {\rm{ \mathsf{π} }} z}{M}\right)\right] \end{aligned}$
			$\theta_{m n}=\cos \left(\frac{(2 m+1) {\rm{ \mathsf{π} }} x_{\mathrm{w}}}{2 L}\right) \cos \left(\frac{n {\rm{ \mathsf{π} }} y_{\mathrm{w}}}{B}\right)$
			$\varepsilon_n= \begin{cases}1, & n=0 \\ 2, & n \geqslant 1\end{cases}$
6	3 fixed-head boundary 1 impermeable boundary		$\begin{aligned} s= & \frac{4 Q}{B L M}\left[\sum_{n=1}^{\infty} \sum_{m=0}^{\infty} \frac{\theta_{m n}}{\beta_{m n}^2} \cos \left(\frac{(2 m+1) {\rm{ \mathsf{π} }} x}{2 L}\right) \sin \left(\frac{n {\rm{ \mathsf{π} }} y}{B}\right)+\right. \\ & \left.2 \sum_{k=1}^{\infty} \sum_{n=1}^{\infty} \sum_{m=0}^{\infty} \frac{\xi_k \theta_{m n}}{\beta_{m n k}^2} \cos \left(\frac{(2 m+1) {\rm{ \mathsf{π} }} x}{2 L}\right) \sin \left(\frac{n {\rm{ \mathsf{π} }} y}{B}\right) \cos \left(\frac{k {\rm{ \mathsf{π} }} z}{M}\right)\right] \end{aligned}$
6	3 fixed-head boundary 1 impermeable boundary		$\theta_{m n}=\cos \left(\frac{(2 m+1) {\rm{ \mathsf{π} }} x_{\mathrm{w}}}{2 L}\right) \sin \left(\frac{n {\rm{ \mathsf{π} }} y_{\mathrm{w}}}{B}\right)$
$\beta_{m n k}^2=K_x\left(\frac{(2 m+1) {\rm{ \mathsf{π} }} }{2 L}\right)^2+K_y\left(\frac{n {\rm{ \mathsf{π} }} }{B}\right)^2+K_z\left(\frac{k {\rm{ \mathsf{π} }} }{M}\right)^2+\frac{K_z^{\prime}}{M M^{\prime}}, \beta_{m n}^2=K_x\left(\frac{(2 m+1) {\rm{ \mathsf{π} }} }{2 L}\right)^2+K_y\left(\frac{n {\rm{ \mathsf{π} }} }{B}\right)^2+\frac{K_z^{\prime}}{M M^{\prime}}$

下载: 导出CSV

参考文献(27)

[1]	DUPUIT P J. Études Théoriques et Pratiques sur le Mouvement des Eaux Dans les Canaux Découverts et à Travers les Terrains Perméables: Avec des Considérations Relatives au Régime des Grandes Eaux, au Débouché à Leur Donner, et à la Marche des Alluvions Dans les Rivières à Fond Mobile[M]. Paris: Dunod éditeur, 1863.
[2]	THIEM A. Die ergiebigkeit artesischer bohrlöcher, schachtbrunnen und filtergalerien[J]. Journal fur Gasbeleuchtung und Wasserversorgung, 1870, 13: 450-467.
[3]	HANTUSH M S, JACOB C E. Non-steady radial flow in an infinite leaky aquifer[J]. Eos Transactions American Geophysical Union, 1955, 36(1): 95-100. doi: 10.1029/TR036i001p00095
[4]	JACOB C E. Radial flow in a leaky artesian aquifer[J]. Eos Transactions American Geophysical Union, 1946, 27(2): 198-208. doi: 10.1029/TR027i002p00198
[5]	HANTUSH M S, JACOB C E. Steady three-dimensional flow to a well in a two-layered aquifer[J]. Eos Transactions American Geophysical Union, 1958, 36(2): 286-292.
[6]	HANTUSH M S. Drawdown around a partially penetrating well[J]. Journal of the Hydraulics Division, 1961, 127(1): 83-98.
[7]	HANTUSH M S. Hydraulics of wells[M]//Advances in Hydroscience. New York: Academic Press, 1964: 281-432.
[8]	JAVANDEL I. Analytical solutions in subsurface fluid flow[J]. Geological Society of America, 1982, 189: 223-235.
[9]	CHEN J S, WU C L, LIU C W. Analysis of contaminant transport towards a partially penetrating extraction well in an anisotropic aquifer[J]. Hydrological Processes, 2010, 24(15): 2125-2136.
[10]	DALY C J, MOREL-SEYTOUX H J. An integral transform method for the linearized Boussinesq groundwater flow equation[J]. Water Resources Research, 1981, 17(4): 875-884. doi: 10.1029/WR017i004p00875
[11]	YEO I W, LEE K K. Analytical solution for arbitrarily located multiwells in an anisotropic homogeneous confined aquifer[J]. Water Resources Research, 2003, 39(5): 1133.
[12]	王旭东, 殷宗泽, 宰金珉. 有限区域地下水非稳定流解析解[J]. 南京工业大学学报, 2008, 30(2): 45-50. https://www.cnki.com.cn/Article/CJFDTOTAL-NHXB200802010.htm WANG Xudong, YIN Zongze, ZAI Jinmin. Analytical solution of unsteady groundwater flow in limited areas[J]. Journal of Nanjing Tech University, 2008, 30(2): 45-50. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-NHXB200802010.htm
[13]	CHAN Y K, MULLINEUX N, REED J R. Analytic solutions for drawdowns in rectangular artesian aquifers[J]. Journal of Hydrology, 1976, 31(1/2): 151-160.
[14]	CHAN Y K. Improved image-well technique for aquifer analysis[J]. Journal of Hydrology, 1976, 29(1/2): 149-164.
[15]	YANG L Z, HE F, LI Y, et al. Three-dimensional steady-state closed form solution for multilayered fluid-saturated anisotropic finite media due to surface/internal point source[J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(1): 17-38. doi: 10.1007/s10483-021-2685-9
[16]	姬安召, 王玉风, 张光生. 不对称裂缝单井渗流模型的Green函数构造方法[J]. 应用数学和力学, 2022, 43(4): 424-434. doi: 10.21656/1000-0887.420237 JI Anzhao, WANG Yufeng, ZHANG Guangsheng. A Green's function construction method of the single well seepage model for asymmetric fractures[J]. Applied Mathematics and Mechanics, 2022, 43(4): 424-434. (in Chinese) doi: 10.21656/1000-0887.420237
[17]	黄飞, 马永斌. 移动热源作用下基于分数阶应变的三维弹性体热-机响应[J]. 应用数学和力学, 2021, 42(4): 373-384. doi: 10.21656/1000-0887.400346 HUANG Fei, MA Yongbin. Thermomechanical responses of 3D media under moving heat sources based on fractional-order strains[J]. Applied Mathematics and Mechanics, 2021, 42(4): 373-384. (in Chinese) doi: 10.21656/1000-0887.400346
[18]	孔祥言. 高等渗流力学[M]. 3版. 合肥: 中国科技大学出版社, 2020. KONG Xiangyan. Advanced Seepage Mechanics[M]. 3rd ed. Hefei: University of Science and Technology of China Press, 2020. (in Chinese)
[19]	段汕. 有限Fourier变换在偏微分方程中的应用[J]. 中南民族学院学报, 1999, 18(4): 62-67. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNZK199904019.htm DUAN Shan. Application of finite Fourier transform in partial differential equation[J]. Journal of South Central College for Nationalities, 1999, 18(4): 62-67. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNZK199904019.htm
[20]	姬安召. Newton-非Newton幂律流双区复合水平井压力动态特征分析[J]. 应用数学和力学, 2019, 40(5): 562-573. doi: 10.21656/1000-0887.390252 JI Anzhao. Transient pressure analysis of bi-zone composite horizontal wells with non-Newtonian and Newtonian power-law fluid flow[J]. Applied Mathematics and Mechanics, 2019, 40(5): 562-573. (in Chinese) doi: 10.21656/1000-0887.390252
[21]	DAVIS H F. Fourier Series and Orthogonal Functions[M]. New York: Dover Publications, 1989.
[22]	SNEDDON I N. The Use of Integral Transforms[M]. New York: McGraw-Hill, 1972.
[23]	CHURCHILL R V. Operational Mathematics[M]. New York: McGraw-Hill, 1972.
[24]	杨天行, 付泽周, 刘金山, 等. 地下水流向井的非稳定运动的原理及计算方法[M]. 北京: 地质出版社, 1980. YANG Tianxing, FU Zezhou, LIU Jinshan, et al. Principles and Calculation Methods of Unsteady Ground-Water Flow to Wells[M]. Beijing: Geological Publishing House, 1980. (in Chinese)
[25]	DALY C J, MOREL-SEYTOUX H J. An integral transform method for the linearized Bossinesq groundwater flow equation[J]. Water Resources Research, 1981, 17(4): 875-884.
[26]	郑刚, 曹剑然, 程雪松, 等. 天津第二粉土粉砂微承压含水层回灌试验研究[J]. 岩土工程学报, 2018, 40(4): 592-601. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201804004.htm ZHENG Gang, CAO Jianran, CHENG Xuesong, et al. Experimental study on artificial recharge of second Tianjin silt and silty sand micro-confined aquifer[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 592-601. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201804004.htm
[27]	曹剑然. 天津地区基坑工程中承压层回灌控沉理论与技术研究[D]. 博士学位论文. 天津: 天津大学, 2018. CAO Jianran. Study on the theory and technology of recharge and subsidence control of confined layer in excavation engineering in Tianjin area[D]. PhD Thesis. Tianjin: Tianjin University, 2018. (in Chinese)