磁场作用功能梯度壳体磁弹耦合动力学模型

胡宇达; 廖峰

doi:10.21656/1000-0887.440048

磁场作用功能梯度壳体磁弹耦合动力学模型

doi: 10.21656/1000-0887.440048

胡宇达^{1, 2, ,},
廖峰^{1, 2}

1.
燕山大学建筑工程与力学学院，河北秦皇岛 066004
2.
燕山大学河北省重型装备与大型结构力学可靠性重点实验室，河北秦皇岛 066004

基金项目:

国家自然科学基金项目 12172321

河北省自然科学基金项目 A2020203007

详细信息

通讯作者:
胡宇达(1968—)，男，教授，博士，博士生导师(通讯作者. E-mail: huyuda03@163.com)

中图分类号: O322;O343.7
计量
- 文章访问数: 381
- HTML全文浏览量: 175
- PDF下载量: 49
- 被引次数: 0
出版历程
- 收稿日期: 2023-02-27
- 修回日期: 2023-05-24
- 刊出日期: 2023-11-01

A Magnetoelastic Coupling Dynamical Model for Functional Gradient Shells Under Magnetic Field Actions

HU Yuda^{1, 2
, ,},
LIAO Feng^{1, 2}

1.
School of Civil Engineering and Mechanics, Yanshan University, Qinhuangdao, Hebei 066004, P.R.China
2.
Hebei Key Laboratory of Mechanical Reliability for Heavy Equipment and Large Structures, Yanshan University, Qinhuangdao, Hebei 066004, P.R.China

摘要

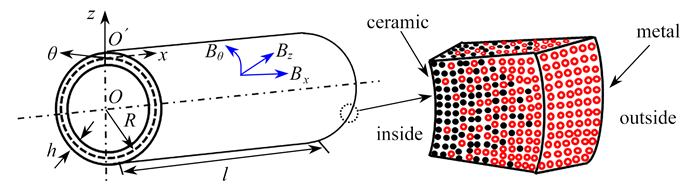
摘要: 针对电磁场环境中金属-陶瓷功能梯度圆柱壳体结构，基于物理中面下的几何关系和Hooke定律，确定了圆柱薄壳体的非线性本构关系.根据Kirchhoff-Love弹性理论，给出了非均质弹性壳体的变形应变能、动能及其变分运算式.基于电磁弹性理论，得出了电磁场作用下磁性功能梯度壳体所受涡流Lorentz力和磁化力模型.应用Hamilton广义变分原理，建立功能梯度薄壳体的磁弹性耦合非线性振动方程组，得出了描述功能梯度结构的具有变形场与电磁场耦合特征的动力学理论模型.通过对磁场中功能梯度壳体固有振动问题的举例分析，得到了壳体振动特征方程和固有频率变化规律，表明磁场和材料体积分数指数的增大能够使频率值减小，而在周向波数影响曲线中出现频率最小值的情形.研究方法可为多场耦合系统理论建模及动力学分析提供参考.
- 功能梯度圆柱壳 /
- 磁弹性 /
- 动力学模型 /
- 电磁场 /
- Hamilton变分原理
Abstract: For metal-ceramic functional gradient cylindrical shells in electromagnetic fields, the nonlinear constitutive relations were determined based on the geometry and Hooke's law on the physical neutral surface. According to the Kirchhoff-Love theory, the strain energy expression and the kinetic energy expression with its variational operator were given for the heterogeneous elastic shell. The model of the eddy current Lorentz force and the magnetization force for ferromagnetic functional gradient shells under electromagnetic field actions, was derived with the electromagnetic elasticity theory. The magnetoelastic coupling nonlinear vibration equations for the shell were obtained by means of Hamilton's variational principle, and the dynamical model describing the coupling characteristics of the deformation field and the electromagnetic field was established for functional gradient structures. Through numerical examples for natural vibrations of functional gradient shells, the characteristic equation and the natural frequency variation law were obtained. The results show that, the natural frequency decreases with the magnetic induction intensity and the material volume fraction index, and the phenomenon of minimum frequency will occur in the circumferential wave number influence curves. This study provides a reference for the theoretical modeling and dynamic analysis of multi-field coupling systems.
- functional gradient cylindrical shell /
- magnetoelasticity /
- dynamical model /
- electromagnetic field /
- Hamilton's variational principle

HTML全文

图 1 磁场中FGM圆柱壳模型

Figure 1. The model for the FGM cylindrical shell in a magnetic field

下载: 全尺寸图片幻灯片

图 2 固有频率-周向波数特征曲线

Figure 2. Characteristic curves of natural frequency-circumferential wave numbers

下载: 全尺寸图片幻灯片

图 3 固有频率-磁感应强度特征曲线

Figure 3. Characteristic curves of natural frequency-magnetic induction intensities

下载: 全尺寸图片幻灯片

图 4 固有频率-体积分数指数特征曲线

Figure 4. Characteristic curves of natural frequency-volume fraction indexes

下载: 全尺寸图片幻灯片

图 5 不同磁感应强度FGM圆柱壳时程响应

Figure 5. Time history response diagrams of the FGM cylindrical shell with different magnetic induction intensities

下载: 全尺寸图片幻灯片

图 6 FGM圆柱壳功率谱

Figure 6. Power spectrum diagrams of the FGM cylindrical shell

下载: 全尺寸图片幻灯片

表 1 不锈钢/镍FGM圆柱壳固有频率随体积分数指数变化

Table 1. Natural frequencies of stainless steel/nickel FGM shells with different volume fraction indexes

(m, n)	sources	ω/Hz
(m, n)	sources	N=0	N=0.5	N=1	N=2	N=5
(1, 7)	ref. [35]	580.70	570.25	565.46	560.93	556.45
	ref. [34]	585.79	575.27	570.48	565.92	561.40
	present	590.17	579.46	574.46	569.64	564.99
(1, 8)	ref. [35]	763.98	750.12	743.82	737.86	731.97
	ref. [34]	759.91	746.28	740.07	734.18	728.31
	present	771.37	757.37	750.82	744.54	738.46

下载: 导出CSV

参考文献(35)

[1]	沈惠申. 功能梯度复合材料板壳结构的弯曲、屈曲和振动[J]. 力学进展, 2004, 34(1): 53-60. https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ200401006.htm SHEN Huishen. Bending, buckling and vibration of functionally graded plates and shells[J]. Advances in Mechanics, 2004, 34(1): 53-60. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ200401006.htm
[2]	YANG B, CHEN W Q, DING H J. Approximate elasticity solutions for functionally graded circular plates subject to a concentrated force at the center[J]. Mathematics and Mechanics of Solids, 2014, 19(3): 277-288. doi: 10.1177/1081286512463572
[3]	LIU N W, SUN Y L, CHEN W Q, et al. 3D elasticity solutions for stress field analysis of FGM circular plates subject to concentrated edge forces and couples[J]. Acta Mechanica, 2019, 230(8): 2655-2668. doi: 10.1007/s00707-019-02412-z
[4]	YOUSEFITABAR M, MATAPOURI M K. Thermally induced buckling of thin annular FGM plates[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2017, 39(1): 969-980.
[5]	TRABELSI S, FRIKHA A, ZGHAL S, et al. Thermal post-buckling analysis of functionally graded material structures using a modified FSDT[J]. International Journal of Mechanical Sciences, 2018, 144(8): 74-89.
[6]	CHAN D Q, LONG V D, DUC N D. Nonlinear buckling and postbuckling of FGM shear-deformable truncated conical shells reinforced by FGM stiffeners[J]. Mechanics of Composite Materials, 2019, 54(6): 745-764. doi: 10.1007/s11029-019-9780-x
[7]	曹志远. 不同条件功能梯度矩形板固有频率解的一般表达式[J]. 复合材料学报, 2005, 22(5): 172-177. https://www.cnki.com.cn/Article/CJFDTOTAL-FUHE200505028.htm CAO Zhiyuan. Unified expression of natural frequency solutions for functionally graded composite rectangular plates under various boundary conditions[J]. Acta Materiae Compositae Sinica, 2005, 22(5): 172-177. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FUHE200505028.htm
[8]	TU T M, QUOC T H, VAN-LONG N. Vibration analysis of functionally graded plates using the eight-unknown higher order shear deformation theory in thermal environments[J]. Aerospace Science and Technology, 2018, 84(5): 698-711.
[9]	HU Y D, ZHANG Z Q. The bifurcation analysis on the circular functionally graded plate with combination resonances[J]. Nonlinear Dynamics, 2012, 67(3): 1779-1790. doi: 10.1007/s11071-011-0105-4
[10]	ZHANG W, HAO Y X, YANG J. Nonlinear dynamics of FGM circular cylindrical shell with clamped-clamped edges[J]. Composite Structures, 2012, 94(3): 1075-1086. doi: 10.1016/j.compstruct.2011.11.004
[11]	AN F X, CHEN F Q. Multi-pulse chaotic motions of functionally graded truncated conical shell under complex loads[J]. Nonlinear Dynamics, 2017, 89(3): 1753-1778. doi: 10.1007/s11071-017-3550-x
[12]	SAHU N K, BISWAL D K, JOSEPH S V, et al. Vibration and damping analysis of doubly curved viscoelastic-FGM sandwich shell structures using FOSDT[J]. Structures, 2020, 26: 24-38. doi: 10.1016/j.istruc.2020.04.007
[13]	LI X, DU C C, LI Y H. Parametric resonance of a FG cylindrical thin shell with periodic rotating angular speeds in thermal environment[J]. Applied Mathematical Modelling, 2018, 59(7): 393-409.
[14]	ZHANG D G, ZHOU Y H. A theoretical analysis of FGM thin plates based on physical neutral surface[J]. Computational Materials Science, 2008, 44(2): 716-720. doi: 10.1016/j.commatsci.2008.05.016
[15]	ZHANG D G. Nonlinear bending analysis of FGM beams based on physical neutral surface and high order shear deformation theory[J]. Composite Structure, 2013, 100: 121-126. doi: 10.1016/j.compstruct.2012.12.024
[16]	ZHANG D G. Nonlinear static analysis of FGM infinite cylindrical shallow shells based on physical neutral surface and high order shear deformation theory[J]. Applied Mathematical Modelling, 2015, 39(5/6): 1587-1596.
[17]	MIYA K, HARA K, SOMEYA K. Experimental and theoretical study on magnetoelastic buckling of a ferromagnetic cantilevered beam-plate[J]. Journal of Applied Mechanics, 1978, 45(2): 355-360. doi: 10.1115/1.3424301
[18]	刘旭, 姚林泉. 热环境中旋转功能梯度纳米环板的振动分析[J]. 应用数学和力学, 2020, 41(11): 1224-1236. doi: 10.21656/1000-0887.410090 LIU Xu, YAO Linquan. Vibration analysis of rotating functionally gradient nano annular plates in thermal environment[J]. Applied Mathematics and Mechanics, 2020, 41(11): 1224-1236. (in Chinese) doi: 10.21656/1000-0887.410090
[19]	陈明飞, 刘坤鹏, 靳国永, 等. 面内功能梯度三角形板等几何面内振动分析[J]. 应用数学和力学, 2020, 41(2): 156-170. doi: 10.21656/1000-0887.400171 CHEN Mingfei, LIU Kunpeng, JIN Guoyong, et al. Isogeometric in-plane vibration analysis of functionally graded triangular plates[J]. Applied Mathematics and Mechanics, 2020, 41(2): 156-170. (in Chinese) doi: 10.21656/1000-0887.400171
[20]	WANG X Z, LEE J S, ZHENG X J. Magneto-thermo-elastic instability of ferromagnetic plates in thermal and magnetic fields[J]. International Journal of Solids and Structures, 2003, 40(22): 6125-6142. doi: 10.1016/S0020-7683(03)00297-X
[21]	MOHAJERANI S A, MOHAMMADZADEH A, NIKKHAH-BAHRAMI M N. An exact solution for vibration analysis of soft ferromagnetic rectangular plates under the influence of magnetic field with levy type boundary conditions[J]. Journal of Solid Mechanics, 2017, 9(1): 186-197.
[22]	胡宇达, 张金志. 轴向运动载流导电板磁热弹性耦合动力学方程[J]. 力学学报, 2013, 45(5): 792-796. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201305020.htm HU Yuda, ZHANG Jinzhi. Magneto-thermo-elastic coupled dynamics equations of axially moving carry current plate in magnetic field[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(5): 792-796. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201305020.htm
[23]	HU Y D, CAO T X, XIE M X. Magnetic-structure coupling dynamic model of a ferromagnetic plate parallel moving in air-gap magnetic field[J]. Acta Mechanica Sinica, 2022, 38(10): 522084. doi: 10.1007/s10409-022-22084-x
[24]	胡宇达, 刘超. 线载和弹性支承作用面内运动薄板磁固耦合双重共振[J]. 应用数学和力学, 2021, 42(7): 713-722. doi: 10.21656/1000-0887.410202 HU Yuda, LIU Chao. Double resonance of magnetism-solid coupling of in-plane moving thin plates with linear loads and elastic supports[J]. Applied Mathematics and Mechanics, 2021, 42(7): 713-722. (in Chinese) doi: 10.21656/1000-0887.410202
[25]	沈璐璐, 蔡方圆, 杨博. 功能梯度压电板柱面弯曲的弹性力学解[J]. 应用数学和力学, 2023, 44(3): 272-281. doi: 10.21656/1000-0887.430224 SHEN Lulu, CAI Fangyuan, YANG Bo. Elasticity solutions for cylindrical bending of functionally graded piezoelectric material plates[J]. Applied Mathematics and Mechanics, 2023, 44(3): 272-281. (in Chinese) doi: 10.21656/1000-0887.430224
[26]	MIKILYANA M, MARZOCCA P. Dynamic instability of electroconductive cylindrical shell in a magneticfield[J]. International Journal of Solids and Structures, 2019, 160: 168-176.
[27]	MOLCHENKO L V, LOOS I I, VASILEVA L Y, et al. Magnetoelastic deformation of isotropic variable-stiffness shells of revolution: allowing for joule heat and geometrical nonlinearity[J]. International Applied Mechanics, 2020, 56(2): 198-207.
[28]	LI Z, WANG Q S, QIN B, et al. Vibration and acoustic radiation of magneto-electro-thermo- elastic functionally graded porous plates in the multi-physics fields[J]. International Journal of Mechanical Sciences, 2020, 185(11): 105850.
[29]	MEHDITABAR A, RAHIMI G H, ANSARI-SADRABADI S. Three-dimensional magneto-thermo-elastic analysis of functionally graded cylindrical shell[J]. Applied Mathematics and Mechanics(English Edition), 2017, 38(4): 479-494.
[30]	LIU Y F, QIN Z Y, CHU F L. Nonlinear forced vibrations of functionally graded piezoelectric cylindrical shells under electric-thermo-mechanicalloads[J]. International Journal of Mechanical Sciences, 2021, 201: 106474.
[31]	DU C C, LI Y H. Nonlinear resonance behavior of functionally graded cylindrical shells in thermal environments[J]. Composite Structures, 2013, 102(8): 164-174.
[32]	ZHANG D G, ZHOU Y H. A theoretical analysis of FGM thin plates based on physical neutralsurface[J]. Computational Materials Science, 2009, 44(2): 716-720.
[33]	梁斌, 项爽, 李戎, 等. 旋转功能梯度圆柱壳振动影响因素研究[J]. 船舶力学, 2013, 17(12): 1460-1472. https://www.cnki.com.cn/Article/CJFDTOTAL-CBLX201312010.htm LIANG Bin, XIANG Shuang, LI Rong, et al. Study of effective factors for the vibration of rotating functionally graded cylindrical shells[J]. Journal of Ship Mechanics, 2013, 17(12): 1460-1472. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CBLX201312010.htm
[34]	SHEN H S. Nonlinear vibration of shear deformable FGM cylindrical shells surrounded by an elasticmedium[J]. Composite Structures, 2012, 94(3): 1144-1154.
[35]	LOY C T, LAM K Y, REDDY J N. Vibration of functionally graded cylindricalshells[J]. International Journal of Mechanical Sciences, 1999, 41(3): 309-324.