求解理想磁流体方程的四阶WENO型熵稳定格式

张成治; 郑素佩; 陈雪; 张蕊

doi:10.21656/1000-0887.440178

求解理想磁流体方程的四阶WENO型熵稳定格式

doi: 10.21656/1000-0887.440178

长安大学理学院，西安 710064

基金项目:

国家自然科学基金项目 11971075

详细信息

作者简介:
张成治(1999—)，男，硕士生(E-mail: zhangchengzhi2021@163.com)

通讯作者:
郑素佩(1978—)，女，副教授，博士，硕士生导师(通讯作者. E-mail: zsp2008@chd.edu.cn)

中图分类号: O241
计量
- 文章访问数: 458
- HTML全文浏览量: 159
- PDF下载量: 50
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-13
- 修回日期: 2023-08-02
- 刊出日期: 2023-11-01

A 4th-Order WENO-Type Entropy Stable Scheme for Ideal Magnetohydrodynamic Equations

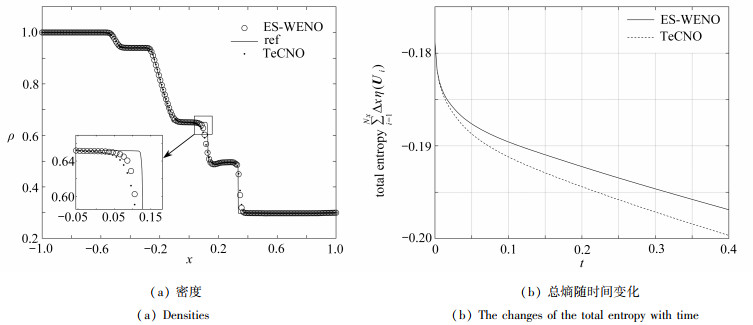
School of Sciences, Chang'an University, Xi'an 710064, P.R.China

摘要

摘要: 构造了一种用于求解理想磁流体方程的四阶熵稳定半离散有限体积格式.该格式空间方向上将高阶熵守恒通量与采用WENO重构的耗散项结合，得到高阶熵稳定通量.通过在耗散项中添加开关函数，使得数值通量具有更低的耗散并且高阶WENO重构满足符号性质.对用来控制磁场散度的源项采用中心格式离散，最终得到与熵守恒通量一致的高阶精度.几个一维、二维算例表明该格式无振荡，鲁棒性强，可以精确捕捉间断.
- 理想磁流体方程 /
- 熵稳定格式 /
- WENO重构 /
- 有限体积法
Abstract: A 4th-order entropy stable semi-discrete finite volume scheme was constructed for ideal magnetohydrodynamic equations. This scheme combines the high-order entropy conservative flux with the dissipation term reconstructed with the WENO scheme in the spatial direction. With a switching function added to the dissipation term, the numerical flux has lower dissipation and the WENO reconstruction satisfies the sign property. The source term used to control the divergence of the magnetic field is discretized with the center difference scheme to obtain high-order accuracy consistent with the entropy conservative flux. Several 1D and 2D cases show that, the scheme has no oscillation and strong robustness, and can accurately capture discontinuities.
- ideal magnetohydrodynamic equation /
- entropy stable scheme /
- WENO reconstruction /
- finite volume method

HTML全文

图 1 Ryu-Jones Riemman问题

Figure 1. The Ryu-Jones Riemman problem

下载: 全尺寸图片幻灯片

图 2 ES-WENO格式在T=0和T=0.4对应的开关函数值

Figure 2. The switch function values corresponding to the ES-WENO scheme at T=0 and T=0.4

下载: 全尺寸图片幻灯片

图 3 Torrilhon Riemman问题

Figure 3. The Torrilhon Riemman problem

下载: 全尺寸图片幻灯片

图 4 二维Orszag-Tang漩涡问题

Figure 4. The 2D Orszag-Tang vortex problem

下载: 全尺寸图片幻灯片

图 5 总熵随时间变化图

Figure 5. The changes of the total entropy with time

下载: 全尺寸图片幻灯片

图 6 第一转子问题

Figure 6. The 1st rotor problem

下载: 全尺寸图片幻灯片

图 7 云-激波相互作用

Figure 7. Cloud-shock interactions

下载: 全尺寸图片幻灯片

表 1 T=5时不同网格数下B₁的L¹, L^∞误差以及对应的收敛阶

Table 1. L¹, L^∞ errors in B₁ at T=5 and corresponding convergence rates for different mesh numbers

N	L¹ error	order	L^∞ error	order
16	9.165E-4		1.477E-3
32	2.838E-5	5.013	4.514E-5	5.032
64	2.100E-6	3.756	3.325E-6	3.763
128	1.320E-7	3.992	2.076E-7	4.001
256	8.337E-9	3.985	1.312E-8	3.984

下载: 导出CSV

参考文献(21)

[1]	GODUNOV S K. Symmetric form of the magnetohydrodynamic equation[J]. Chislennye Metody Mekh Sploshnoi Sredy, 1972, 3(1): 26-34.
[2]	TADMOR E. Numerical viscosity of entropy stable schemes for systems of conservation laws: Ⅰ[J]. Mathematics of Computation, 1987, 49(179): 91-103. doi: 10.1090/S0025-5718-1987-0890255-3
[3]	TADMOR E. Numerical viscosity and the entropy condition for conservative difference schemes[J]. Mathematic of Computation, 1984, 43(168): 369-381. doi: 10.1090/S0025-5718-1984-0758189-X
[4]	ROE P L. Entropy conservation schemes for Euler equations[R]. Lyon, France: Talk at HYP, 2006.
[5]	郑素佩, 李霄, 赵青宇, 等. 求解二维浅水波方程的旋转混合格式[J]. 应用数学和力学, 2022, 43(2): 176-186. doi: 10.21656/1000-0887.420063 ZHENG Supei, LI Xiao, ZHAO Qingyu, et al. A rotated mixed scheme for solving 2D shallow water equations[J]. Applied Mathematics and Mechanics, 2022, 43(2): 176-186. (in Chinese)) doi: 10.21656/1000-0887.420063
[6]	贾豆, 郑素佩. 求解二维Euler方程的旋转通量混合格式[J]. 应用数学和力学, 2021, 42(2): 170-179. doi: 10.21656/1000-0887.410196 JIA Dou, ZHENG Supei. A hybrid scheme of rotational flux for solving 2D Euler equations[J]. Applied Mathematics and Mechanics, 2021, 42(2): 170-179. (in Chinese) doi: 10.21656/1000-0887.410196
[7]	郑素佩, 王令, 王苗苗. 求解二维浅水波方程的移动网格旋转通量法[J]. 应用数学和力学, 2020, 41(1): 42-53. doi: 10.21656/1000-0887.400124 ZHENG Supei, WANG Ling, WANG Miaomiao. Solution of 2D shallow water wave equations with the moving-grid rotating-invariance method[J]. Applied Mathematics and Mechanics, 2020, 41(1): 42-53. (in Chinese) doi: 10.21656/1000-0887.400124
[8]	FJORDHOLM U S, MISHRA S, TADMOR E. Arbitrarily high-order accurate entropy stable essentially nonoscillatory schemes for systems of conservation laws[J]. SIAM Journal on Numerical Analysis, 2012, 50(2): 544-573. doi: 10.1137/110836961
[9]	BISWAS B, DUBEY R K. Low dissipative entropy stable schemes using third order WENO and TVD reconstructions[J]. Advances in Computational Mathematics, 2017, 44(4): 1153-1181.
[10]	DUAN J, TANG H. High-order accurate entropy stable finite difference schemes for one- and two-dimensional special relativistic hydrodynamics[J]. Advances in Applied Mathematics and Mechanics, 2020, 12: 1-29. doi: 10.4208/aamm.OA-2019-0124
[11]	DUAN J, TANG H. High-order accurate entropy stable finite difference schemes for the shallow water magnetohydrodynamics[J]. Journal of Computational Physics, 2021, 431: 110136. doi: 10.1016/j.jcp.2021.110136
[12]	郑素佩, 赵青宇, 封建湖. 基于WENO重构保号的四阶熵稳定格式[J]. 浙江大学学报(理学版), 2022, 49(3): 329-335. https://www.cnki.com.cn/Article/CJFDTOTAL-HZDX202203010.htm ZHENG Supei, ZHAO Qingyu, FENG Jianhu. The fourth order entropy stable scheme based on sign-preserving WENO reconstruction[J]. Journal of Zhejiang University (Science Edition), 2022, 49(3): 329-335. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HZDX202203010.htm
[13]	DUAN J, TANG H. Entropy stable adaptive moving mesh schemes for 2D and 3D special relativistic hydrodynamics[J]. Journal of Computational Physics, 2021, 426: 109949.
[14]	WINTERS A R, GASSNER G J. Affordable, entropy conserving and entropy stable flux functions for the ideal MHD equations[J]. Journal of Computational Physics, 2015, 304: 72-108.
[15]	CHANDRASHEKAR P, KLINGENBERG C. Entropy stable finite volume scheme for ideal compressible MHD on 2-D Cartesian meshes[J]. SIAM Journal on Numerical Analysis, 2016, 54(2): 1313-1340.
[16]	翟梦情, 李琦, 郑素佩. 求解一维理想磁流体方程的移动网格熵稳定格式[J]. 计算力学学报, 2023, 40(2): 229-236. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG202302010.htm ZHAI Mengqing, LI Qi, ZHENG Supei. A moving-grid entropy stable scheme for the 1D ideal MHD equations[J]. Chinese Journal of Computational Mechanics, 2023, 40(2): 229-236. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG202302010.htm
[17]	LIU Y, SHU C W, ZHANG M. Entropy stable high order discontinuous Galerkin methods for ideal compressible MHD on structured meshes[J]. Journal of Computational Physics, 2018, 354: 163-178.
[18]	SHU C W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes[J]. Acta Numerica, 2020, 29: 701-762.
[19]	SHU C W, OSHER S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J]. Journal of Computational Physics, 1989, 77(2): 439-471.
[20]	ORSZAG S A, TANG C M. Small-scale structure of two-dimensional magnetohydrodynamic turbulence[J]. Journal of Fluid Mechanics, 1979, 90(1): 129-143.
[21]	BALSARA D S, SPICER D S. A staggered mesh algorithm using high order Godunov fluxes to ensure solenoidal magnetic fields in magnetohydrodynamic simulations[J]. Journal of Computational Physics, 1999, 149(2): 270-292.