考虑挠曲电效应的薄板声学超材料隔声特性研究

杨莎莎; 彭聪; 孟晗; 沈承

doi:10.21656/1000-0887.450115

考虑挠曲电效应的薄板声学超材料隔声特性研究

doi: 10.21656/1000-0887.450115

杨莎莎^{1, 2, 3,},
彭聪^{2, 4},
孟晗^{2, 4},
沈承^{2, 4, ,}

1.
南京工业职业技术大学机械工程学院，南京 210023
2.
南京航空航天大学航空航天结构力学及控制全国重点实验室，南京 210016
3.
江苏省精密制造技术工程研发中心，南京 210023
4.
南京航空航天大学多功能轻量化材料与结构工信部重点实验室，南京 210016

(我刊青年编委孟晗来稿)

基金项目:

国家自然科学基金 12202183

国家重点研发计划 2023YFB4604800

详细信息

作者简介:
杨莎莎(1986—)，女，讲师，博士(E-mail: 2016100849@niit.edu.cn)

通讯作者:
沈承(1986—)，男，副教授，博士(通讯作者. E-mail: cshen@nuaa.edu.cn)

中图分类号: O32
计量
- 文章访问数: 190
- HTML全文浏览量: 70
- PDF下载量: 37
- 被引次数: 0
出版历程
- 收稿日期: 2024-04-25
- 修回日期: 2024-06-05
- 刊出日期: 2024-08-01

Study on Sound Insulation Characteristics of Thin Plate Acoustic Metamaterials With Flexoelectric Effects

YANG Shasha^{1, 2, 3
,},
PENG Cong^{2, 4},
MENG Han^{2, 4},
SHEN Cheng^{2, 4
, ,}

1.
School of Mechanical Engineering, Nanjing Vocational University of Industry Technology, Nanjing 210023, P.R.China
2.
State Key Laboratory of Mechanics and Control for Aerospace Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R.China
3.
Jiangsu Province Precision Manufacturing Engineering and Technology Research Center, Nanjing 210023, P.R.China
4.
MIIT Key Laboratory of Multifunctional Lightweight Materials and Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R.China

(Contributed by MENG Han, M.AMM Youth Editorial Board)

摘要

摘要: 区别于传统的压电效应，当结构尺寸减小到微纳米尺度时，一种新的力电耦合效应——挠曲电效应将无法被忽略. 该文利用变分原理推导了考虑挠曲电效应的薄板声学超材料结构隔声问题的控制方程和边界条件，基于Kirchhoff薄板理论预测了薄板质量块结构的隔声曲线，系统讨论了挠曲电效应、几何尺寸、质量密度等参数对结构隔声性能的影响. 结果表明，当结构尺寸减小到微纳米尺度时，挠曲电效应显著增加了隔声曲线的隔声谷值和峰值频率，因此考虑挠曲电效应是十分有必要的. 该文的工作有望为微机电系统的噪声控制研究提供理论基础.
- 挠曲电效应 /
- 薄板超材料 /
- 隔声特性
Abstract: When the structure size is reduced to the micro-and nano-scale, a new mechanoelectric coupling effect, the flexoelectric effect, cannot be ignored. The governing equations and boundary conditions for the sound insulation problem of thin plate acoustic metamaterial structure with the flexoelectric effects were derived by means of the variational principle. The sound insulation curves of thin plate mass blocks were predicted based on the Kirchhoff theory. The effects of flexural effects, geometric sizes and mass densities on the sound insulation performances of the structure were systematically discussed. The results show that, for the micro-and nano-scale structure sizes, the flexoelectric effect significantly increases the sound insulation valley values and peak frequencies of the sound insulation curves, so it is necessary to consider the flexoelectric effects. This work provides a theoretical basis for the research of noise control in MEMS.
- flexoelectric effect /
- thin plate metamaterial /
- sound insulation characteristic
edited-by

edited-by
注释:

1) (我刊青年编委孟晗来稿)

HTML全文

图 1 附加薄板质量块结构示意图

Figure 1. The additional sheet mass block structure diagram

下载: 全尺寸图片幻灯片

图 2 薄板质量块结构平面示意图

Figure 2. Structural plane diagram of the sheet mass block

下载: 全尺寸图片幻灯片

图 3 考虑挠曲电效应与经典理论的隔声曲线对比

Figure 3. The sound insulation curve of the flexural effect is compared with that of the classical theory

下载: 全尺寸图片幻灯片

图 4 第一隔声谷/峰值频率随薄板边长/厚度的变化曲线

Figure 4. The 1st sound insulation valley/peak frequency curves with the sheet side length/thickness

下载: 全尺寸图片幻灯片

图 5 薄板尺寸对隔声曲线的影响

Figure 5. Influences of sheet sizes on sound insulation curves

下载: 全尺寸图片幻灯片

图 6 薄板面密度对隔声曲线的影响

Figure 6. Effects of thin plate surface densities on sound insulation curves

下载: 全尺寸图片幻灯片

图 7 质量块面密度对隔声曲线的影响

Figure 7. Influences of mass block surface densities on sound insulation curves

下载: 全尺寸图片幻灯片

图 8 质量块大小对隔声曲线的影响

Figure 8. Influences of mass block sizes on sound insulation curves

下载: 全尺寸图片幻灯片

表 1 薄板质量块材料参数和结构参数^[16]

Table 1. Material and structural parameters of the sheet mass block^[16]

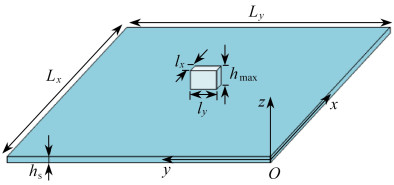
parameter	value
plate length	L_x=500 nm
plate width	L_y=500 nm
plate density	ρ_s=7 500 kg/m³
plate thickness	h_s=10 nm
mass block length	l_x=50 nm
mass block width	l_y=50 nm
mass block density	ρ_mass=7 550 kg/m³
mass block thickness	h_mass=100 nm
elasticity modulus	c₁₁=c₂₂=1.26×10¹¹ N/m², c₁₂=7.95×10¹⁰ N/m², c₆₆=2.325×10¹⁰ N/m²
piezoelectric coefficient	e₃₁₁=e₃₂₂=－6.5 C/m²
flexoelectricity coefficient	f₃₁₁₃=f₃₂₂₃=1×10^－7 C/m
dielectric constant	a₃₃=1.302×10^－8 C/(V·m)

下载: 导出CSV

参考文献(16)

[1]	田源, 葛浩, 卢明辉, 等. 声学超构材料及其物理效应的研究进展[J]. 物理学报, 2019, 68(19): 194301. doi: 10.7498/aps.68.20190850 TIAN Yuan, GE Hao, LU Minghui, et al. Research advances in acoustic metamaterials[J]. Acta Physica Sinica, 2019, 68(19): 194301. (in Chinese) doi: 10.7498/aps.68.20190850
[2]	MA G, YANG M, YANG Z, et al. Low-frequency narrow-band acoustic filter with large orifice[J]. Applied Physics Letters, 2013, 103(1): 011903. doi: 10.1063/1.4812974
[3]	PARK J J, KWAK J H, SONG K. Ultraslow medium with an acoustic membrane-like undamped dynamic vibration absorber for low-frequency isolation[J]. Extreme Mechanics Letters, 2021, 43: 101203. doi: 10.1016/j.eml.2021.101203
[4]	YAO S, ZHOU X, HU G. Investigation of the negative-mass behaviors occurring below a cut-off frequency[J]. New Journal of Physics, 2010, 12(10): 103025. doi: 10.1088/1367-2630/12/10/103025
[5]	MEI J, MA G, YANG M, et al. Dark acoustic metamaterials as super absorbers for low-frequency soun[J]. Nature Communications, 2012, 3: 756. doi: 10.1038/ncomms1758
[6]	KALAEE M, MIRHOSSEINI M, DIETERLE P B, et al. Quantum electromechanics of a hypersonic crystal[J]. Nature Nanotechnology, 2019, 14(4): 334-339. doi: 10.1038/s41565-019-0377-2
[7]	CUENOT S, FRÉTIGNY C, DEMOUSTIER-CHAMPAGNE S, et al. Surface tension effect on the mechanical properties of nanomaterials measured by atomic force microscopy[J]. Physical Review B: Condensed Matter and Materials Physics, 2004, 69(16): 165410. doi: 10.1103/PhysRevB.69.165410
[8]	WANG Z L, SONG J. Piezoelectric nanogenerators based on zinc oxide nanowire arrays[J]. Science, 2006, 312(5771): 242-246. doi: 10.1126/science.1124005
[9]	WANG X, ZHOU J, SONG J, et al. Piezoelectric field effect transistor and nanoforce sensor based on a single ZnO nanowire[J]. Nano Letters, 2006, 6(12): 2768-2772. doi: 10.1021/nl061802g
[10]	JIANG X, HUANG W, ZHANG S. Flexoelectric nano-generator: materials, structures and devices[J]. Nano Energy, 2013, 2(6): 1079. doi: 10.1016/j.nanoen.2013.09.001
[11]	ZHANG Z, JIANG L. Size effects on electromechanical coupling fields of a bending piezoelectric nanoplate due to surface effects and flexoelectricity[J]. Journal of Applied Physics, 2014, 116: 134308. doi: 10.1063/1.4897367
[12]	SHEN S, HU S. A theory of flexoelectricity with surface effect for elastic dielectrics[J]. Journal of the Mechanics and Physics Solids, 2010, 58(5): 665-677. doi: 10.1016/j.jmps.2010.03.001
[13]	王平, 黄庆安, 于虹. 纳机电系统阻尼及噪声研究进展[J]. 电子器件, 2004, 27(3): 527-532. doi: 10.3969/j.issn.1005-9490.2004.03.039 WANG Ping, HUANG Qing'an, YU Hong. Research and ptogress of damping and noise in NEMS[J]. Chinese Journal of Electron Devices, 2004, 27(3): 527-532. (in Chinese) doi: 10.3969/j.issn.1005-9490.2004.03.039
[14]	任树伟, 辛锋先, 卢天健. 考虑尺度效应的微平板声振耦合特性研究[J]. 中国科学: 技术科学, 2014, 44(2): 201-208. REN Shuwei, XIN Fengxian, LU Tianjian. Vibroacoustic characteristics of micro-plates considering scale effect[J]. Scientia Sinica: Technologica, 2014, 44(2): 201-208. (in Chinese)
[15]	原庆丹, 郭俊宏. 一维纳米准晶层合梁的非局部振动、屈曲与弯曲研究[J]. 应用数学和力学, 2024, 45(2): 208-219. YUAN Qingdan, GUO Junhong. Nonlocal vibration, buckling and bending of 1D layered quasicrystal nanobeams[J]. Applied Mathematics and Mechanics, 2024, 45(2): 208-219. (in Chinese)
[16]	GHORBANPOUR A A, SOLTAN A A H, HAGHPARAST E. Flexoelectric and surface effects on vibration frequencies of annular nanoplate[J]. Indian Journal of Physics, 2021, 95(10): 2063-2083. doi: 10.1007/s12648-020-01854-9