Dynamic Modeling and Analysis of the Central Rigid Body-Timoshenko Beam Model Based on Unconstrained Modes
-
摘要:
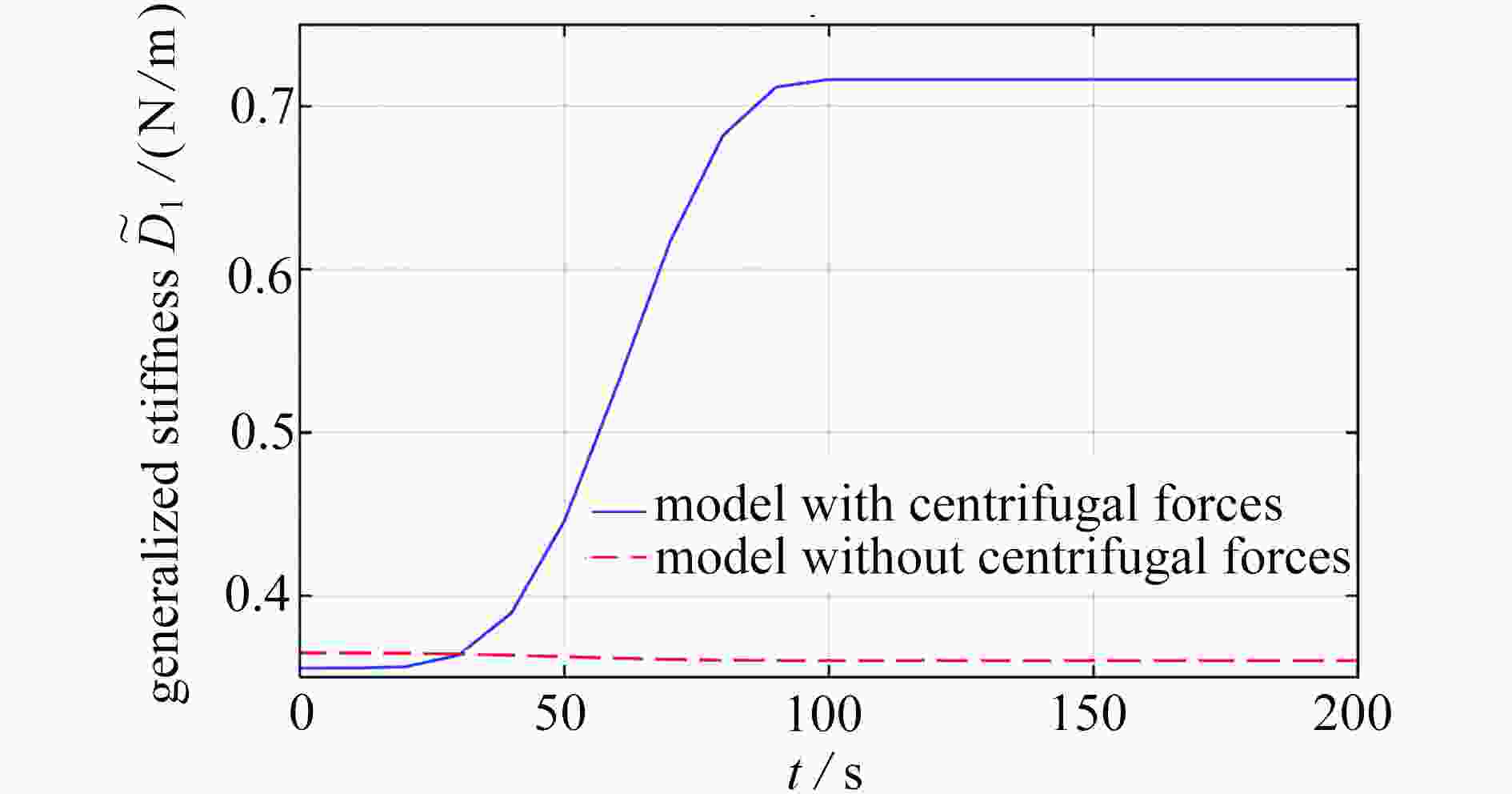
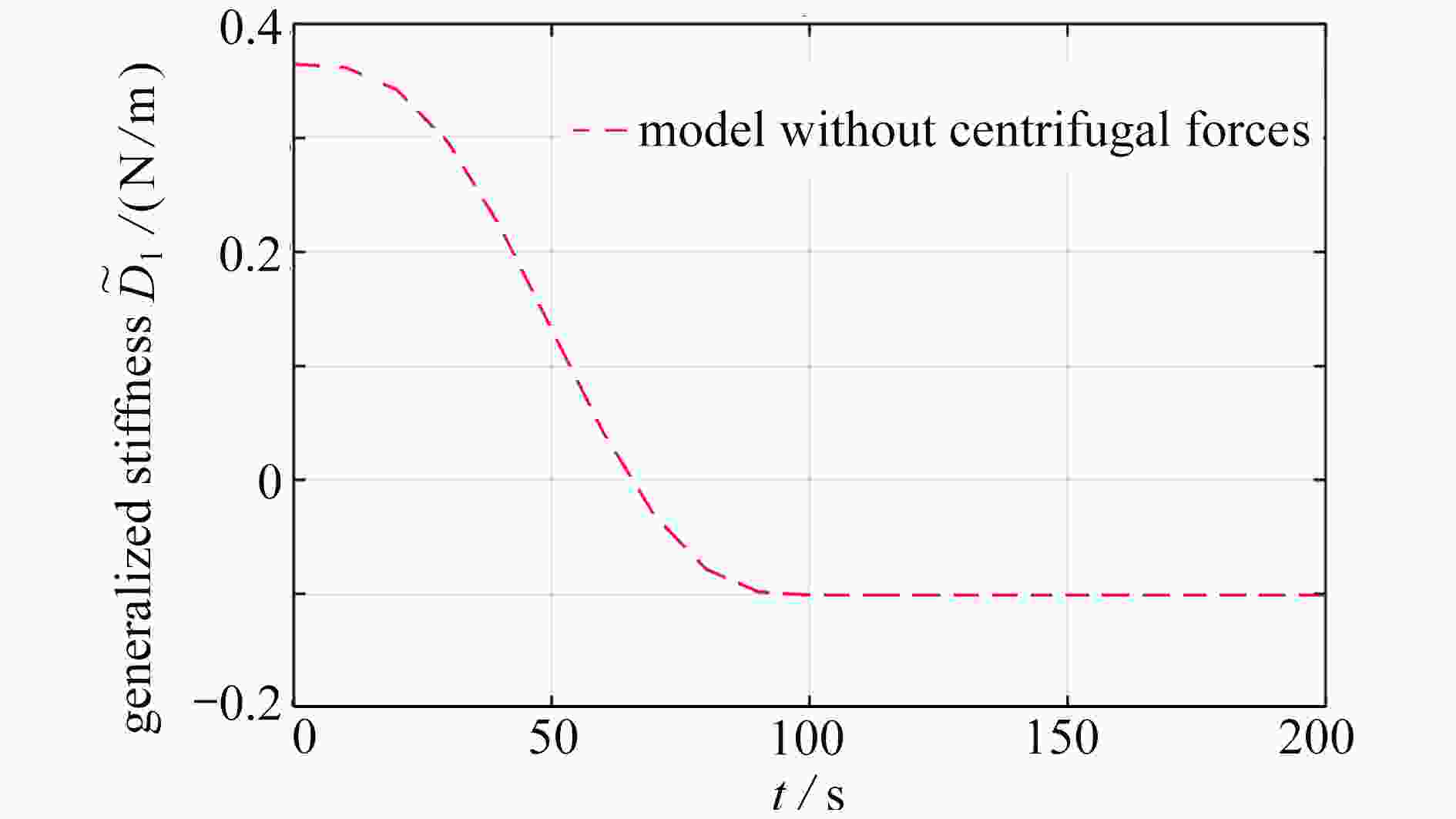
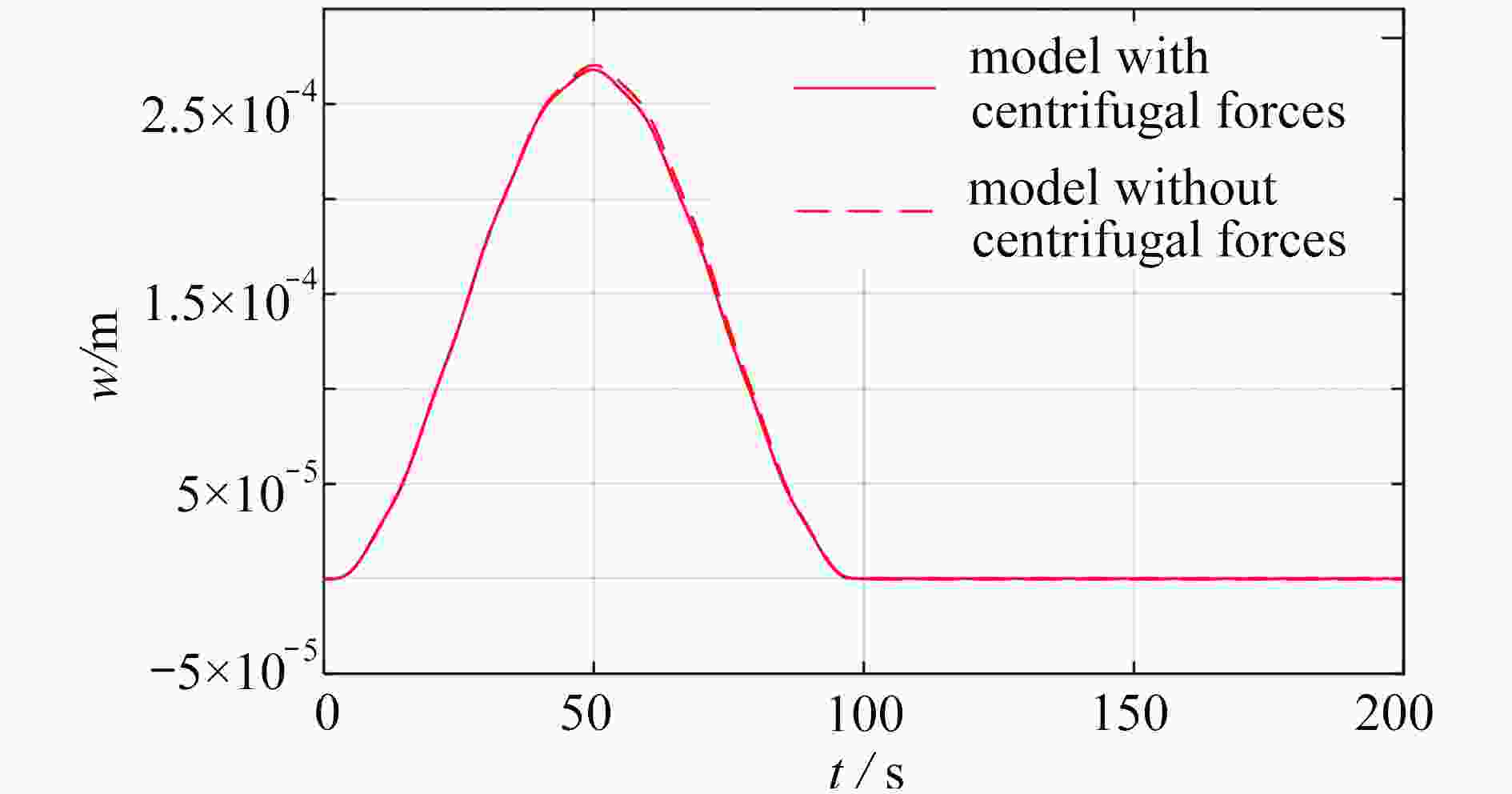
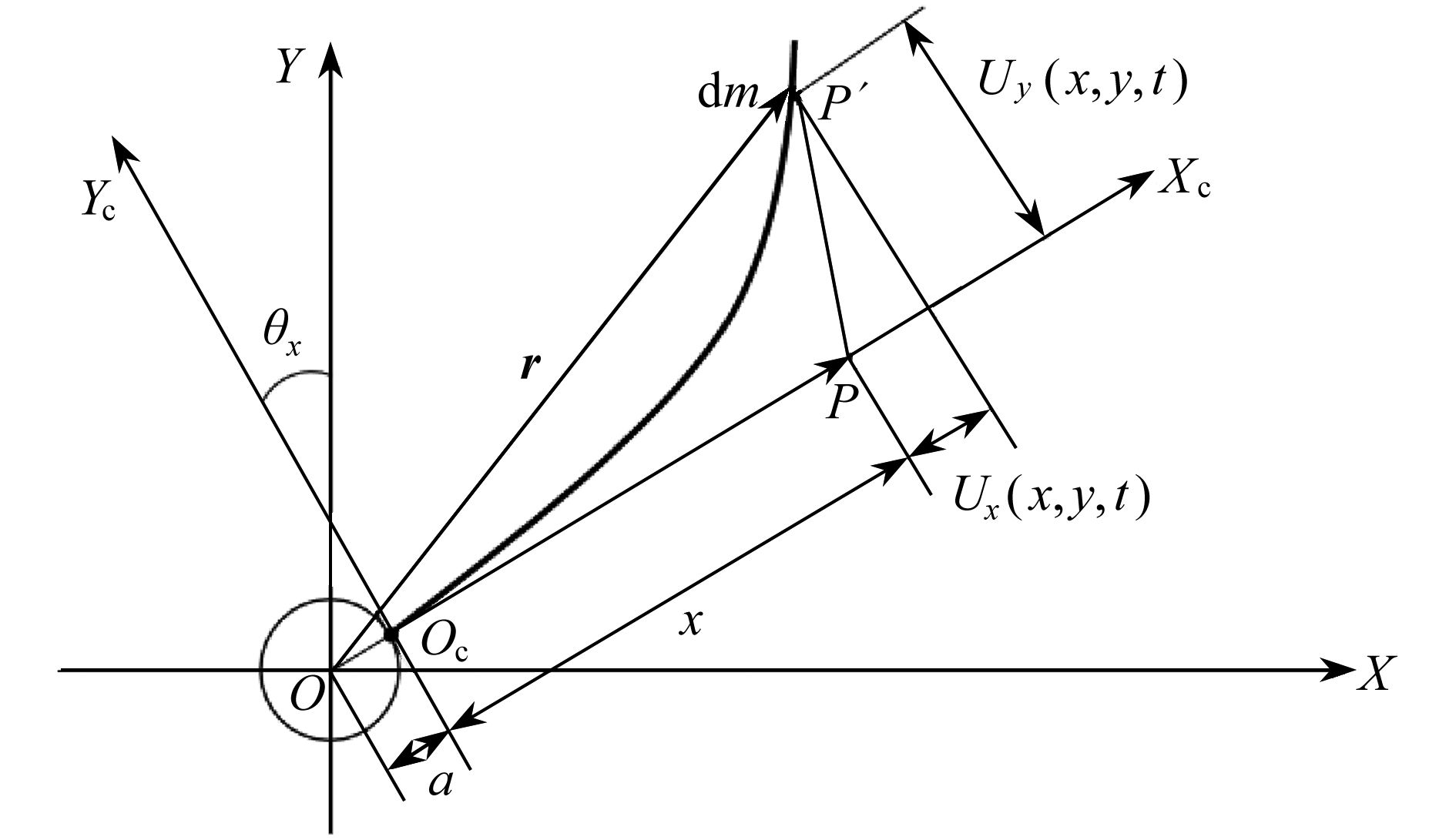
梁的横向变形会导致梁纵向缩短,建模过程中考虑梁横纵变形二次耦合项则存在动力刚化现象,这说明梁的纵向变形会对模型的广义刚度造成影响。对于做旋转运动的梁结构,旋转运动时还会受到离心力的作用而产生轴向拉力,轴向拉力同样也会引起梁的轴向变形,这种影响对粗短梁更加明显。以大范围运动中心刚体-Timoshenko梁模型为研究对象:首先,运用Timoshenko梁理论以及Hamilton原理建立含离心力的动力学模型;其次,引入非约束模态概念,采用Frobenius方法求解非约束模态振型函数以及固有频率;最后,通过数值仿真探究不同恒定转速时非约束模态与约束模态广义刚度的差异和非约束模态条件下离心力对模型的影响。
-
关键词:
- 刚柔耦合 /
- 动力刚化 /
- Timoshenko梁 /
- 非约束模态
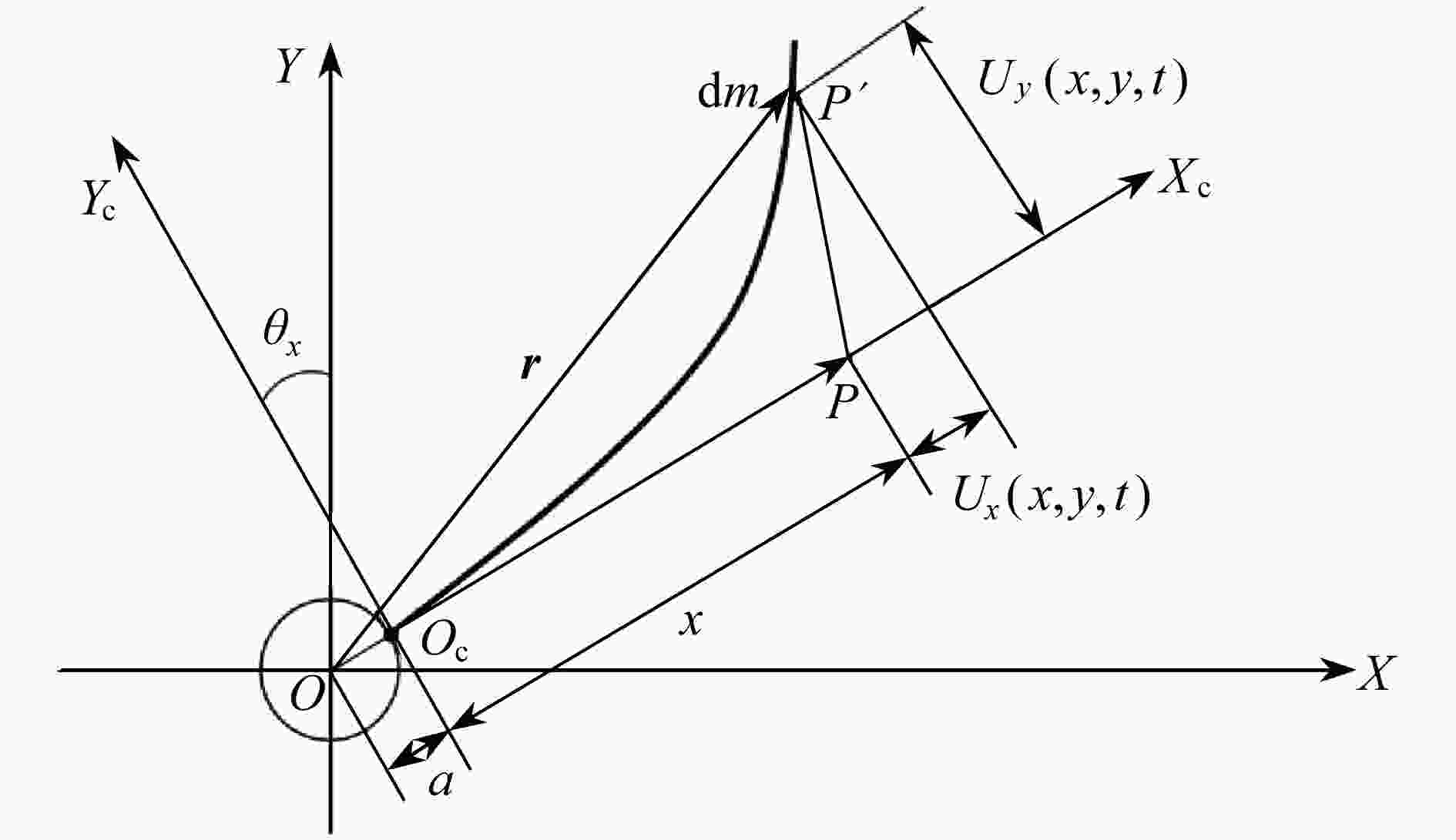
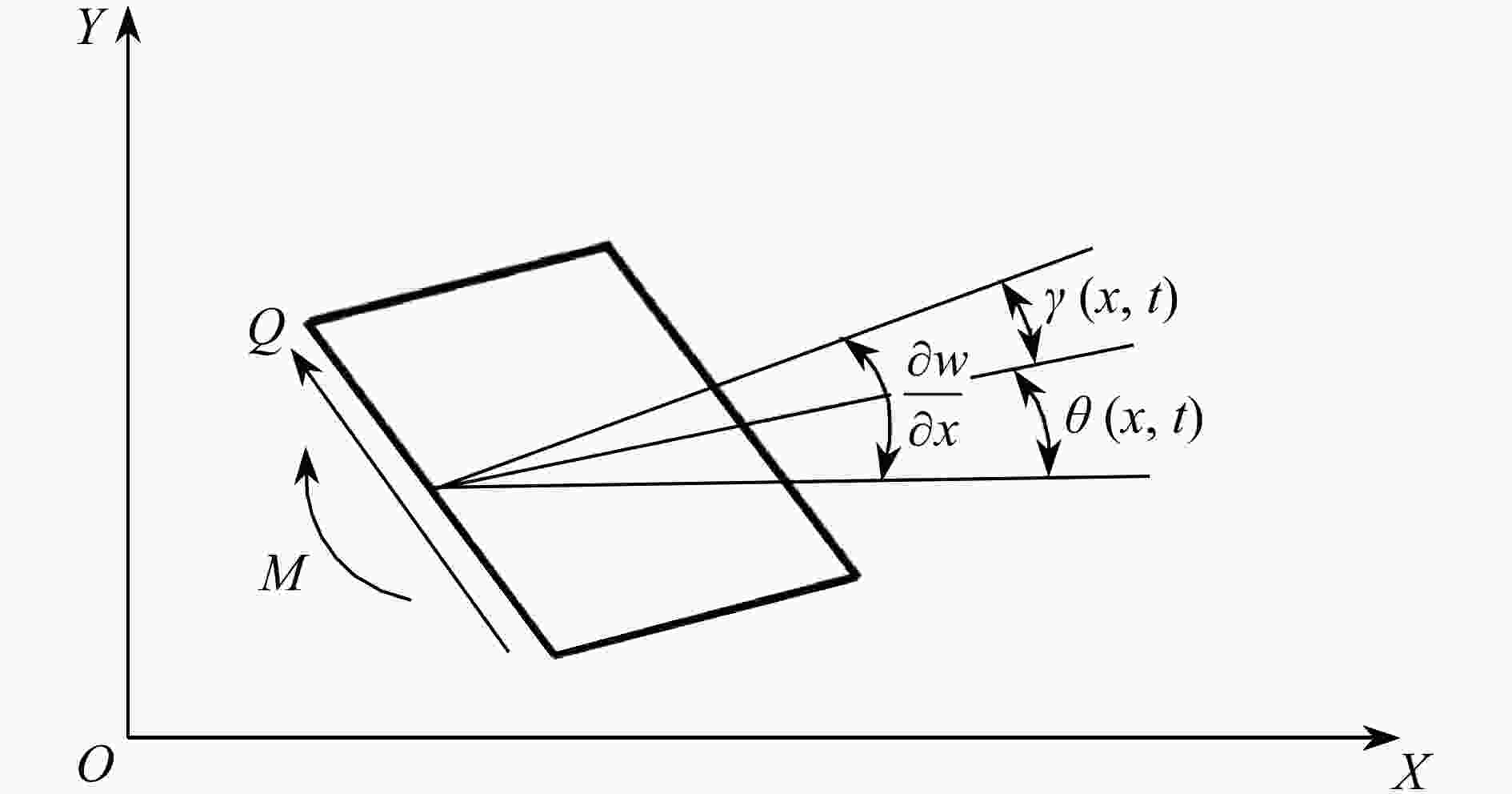
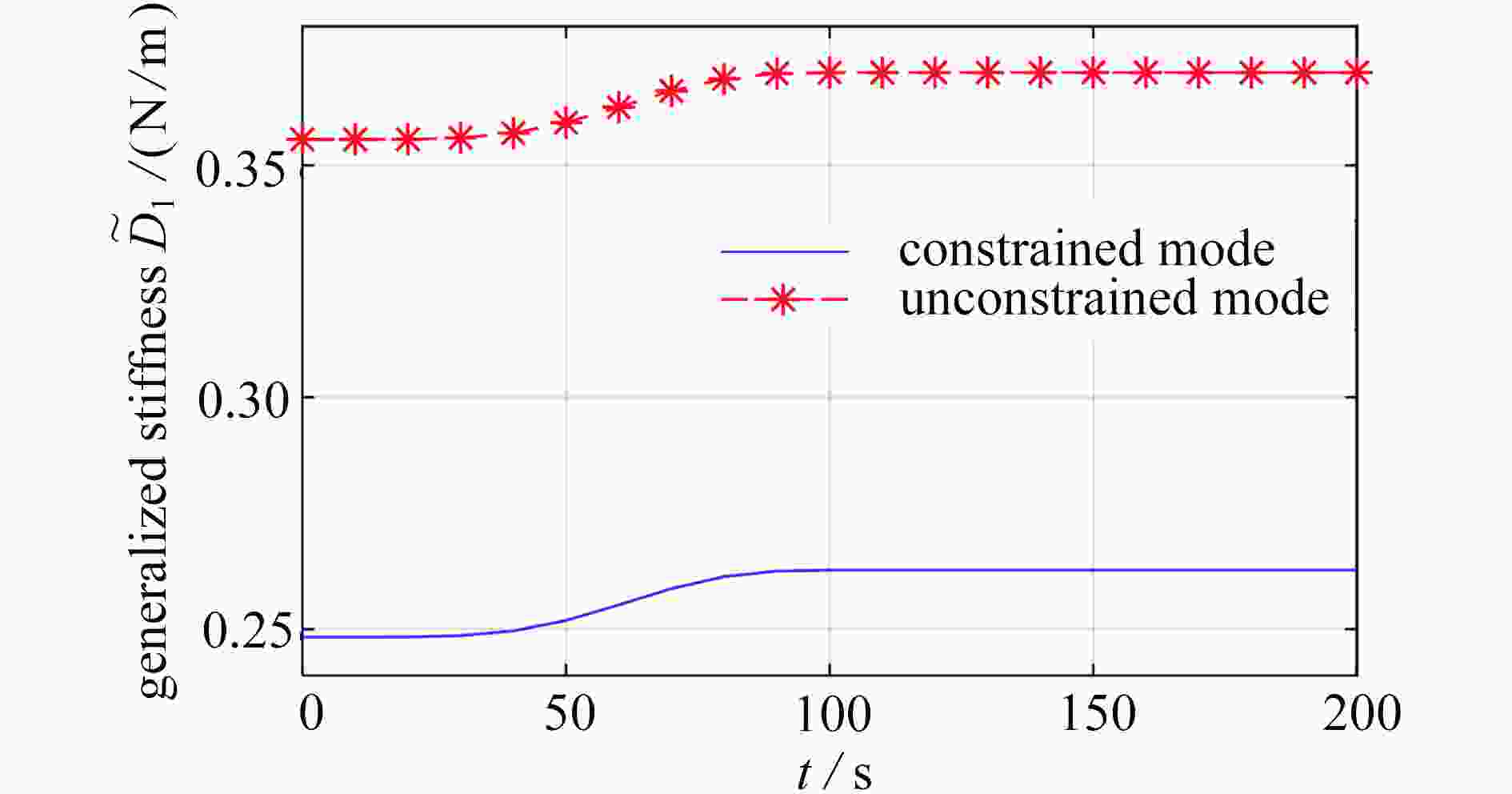
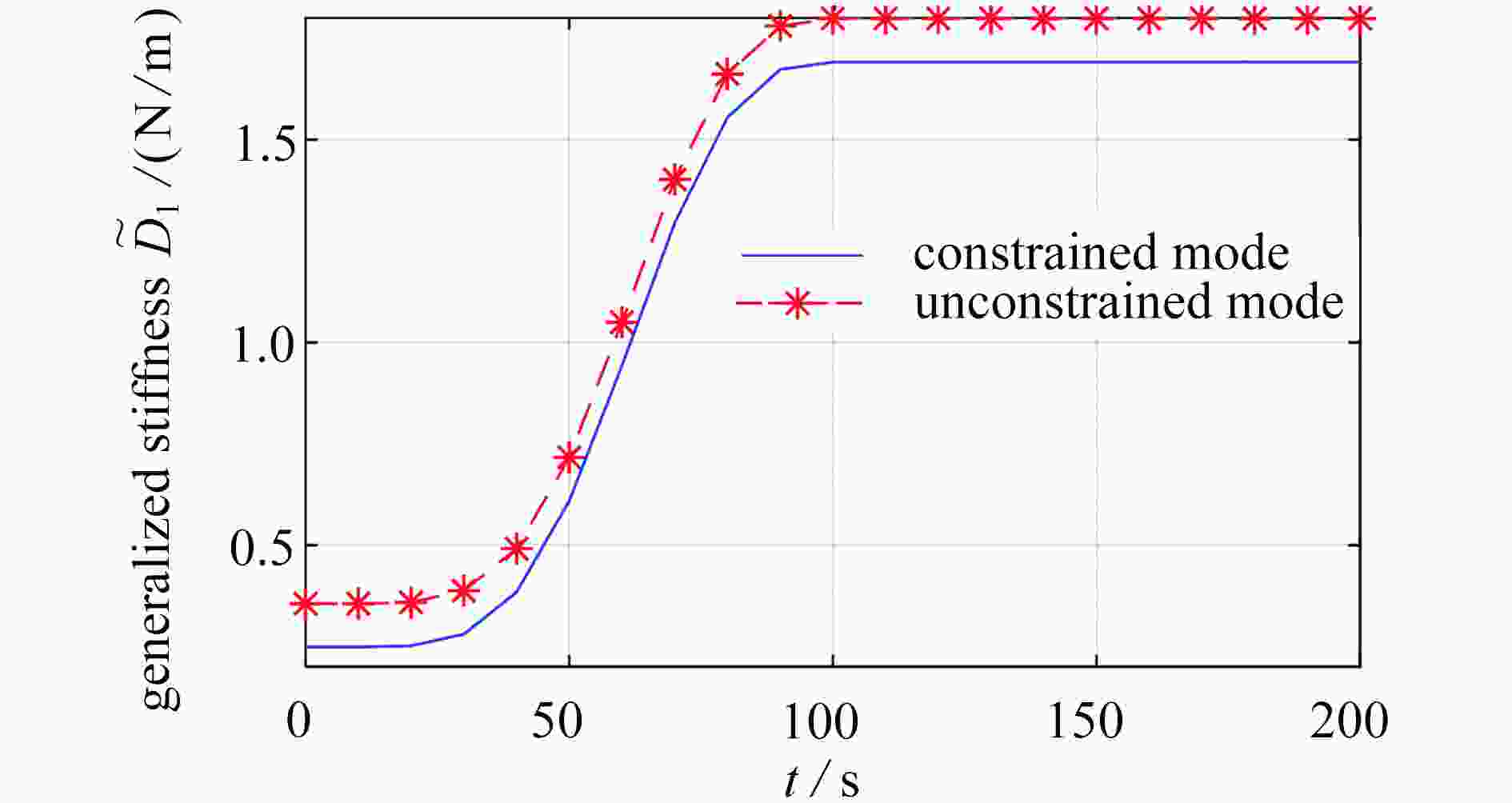
Abstract:The transverse deformation of the beam will lead to the longitudinal shortening deformation, and this transverse-longitudinal deformation coupling will bring the dynamic stiffening effect term on the generalized rigidity of the beam model. For the rotating beam structure, the centrifugal force will cause axial tension, with coupling axial and transverse deformation of the beam and bring additional geometric stiffness, which is more obvious for the thick short beam. The central rigid body-Timoshenko beam model with a large-range-motion center was investigated. Firstly, the dynamic model with centrifugal forces was established by means of the Timoshenko beam theory and the Hamilton principle. Secondly, the unconstrained mode concept was introduced, and the unconstrained mode shape functions and natural frequencies were solved with the Frobenius method. Finally, numerical simulations were carried out to explore the difference of generalized stiffness between the unconstrained mode and the constrained mode at different constant speeds, and the effects of centrifugal forces on the model under unconstrained mode condition were discussed.
-
Key words:
- rigid-flexible coupling /
- dynamic stiffening /
- Timoshenko beam /
- unconstrained mode
-
表 1 Timoshenko 梁参数
Table 1. Parameters of the Timoshenko beam
beam parameter length L / m cross-sectional
area Ab / m2cross-sectional moment
of inertia I / m4Young’s modulus
E/GPadensity
$\rho /({\rm{kg} }/{ {\rm{m} }^{ 3} })$Poisson’s
ratio $\upsilon $shear
coefficient $\kappa $value 0.5 1.6E−3 2.56E−6 163.8 7 850 0.3 5/6 -
[1] 蒋建平, 李东旭. 带太阳帆板航天器刚柔耦合动力学研究[J]. 航空学报, 2006, 27(3): 418-422. (JIANG Jianping, LI Dongxu. Research on rigid-flexible coupling dynamics of spacecraft with solar panel[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(3): 418-422.(in Chinese) doi: 10.3321/j.issn:1000-6893.2006.03.013 [2] 袁秋帆, 王超磊, 齐乃明, 等. 单翼大挠性航天器全局模态动力学建模及试验[J]. 宇航学报, 2019, 40(4): 369-377. (YUAN Qiufan, WANG Chaolei, QI Naiming, et al. Global dynamic modeling for a spacecraft with single large flexible structure and experimental study[J]. Journal of Astronautics, 2019, 40(4): 369-377.(in Chinese) [3] XING Yufeng, QIAO Yuansong, ZHU Dechao, et al. Elastic impact on finite Timoshenko beam[J]. Acta Mechanica Sinica (English Series) , 2002, 18(3): 252-263. [4] 邓军, 陈国平, 张方. 旋转铁木辛柯梁分布动态载荷的时域识别研究[J]. 机械科学与技术, 2011, 30(6): 947-950, 956. (DENG Jun, CHEN Guoping, ZHANG Fang. Identification of distributed dynamic load on a rotating Timoshenko beam in time domain[J]. Mechanical Science and Technology, 2011, 30(6): 947-950, 956.(in Chinese) [5] 张夏阳, 祝明, 武哲. 基于K-V阻尼模型的铁木辛柯梁振动响应分析[J]. 北京航空航天大学学报, 2018, 44(3): 500-507. (ZHANG Xiayang, ZHU Ming, WU Zhe. Vibration response analysis of Timoshenko beam based on K-V damping model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(3): 500-507.(in Chinese) [6] KANE T R, RYAN R, BANERJEE A K. Dynamics of a cantilever beam attached to a moving base[J]. Journal of Guidance, Control and Dynamics, 1987, 10(2): 139-151. [7] 方建士, 章定国. 旋转悬臂梁的刚柔耦合动力学建模与频率分析[J]. 计算力学学报, 2012, 29(3): 333-339. (FANG Jianshi, ZHANG Dingguo. Rigid flexible coupling dynamic modeling and frequency analysis of rotating cantilever beam[J]. Journal of Computational Mechanics, 2012, 29(3): 333-339.(in Chinese) doi: 10.7511/jslx201203007 [8] 章定国, 朱志远. 一类刚柔耦合系统的动力刚化分析[J]. 南京理工大学学报, 2006, 30(1): 21-26. (ZHANG Dingguo, ZHU Zhiyuan. Dynamic rigidity analysis of a rigid flexible coupling system[J]. Journal of Nanjing University of Technology, 2006, 30(1): 21-26.(in Chinese) [9] 方建士, 黎亮, 章定国, 等. 基于刚柔耦合动力学的旋转悬臂梁的频率转向与振型转换特性[J]. 机械工程学报, 2015, 51(17): 59-65. (FANG Jianshi, LI Liang, ZHANG Dingguo, et al. Frequency steering and mode conversion characteristics of rotating cantilever beam based on rigid flexible coupling dynamics[J]. Journal of Mechanical Engineering, 2015, 51(17): 59-65.(in Chinese) doi: 10.3901/JME.2015.17.059 [10] 杨辉, 洪嘉振. 动力刚化问题的实验研究[J]. 力学学报, 2004, 36(1): 118-124. (YANG Hui, HONG Jiazhen. Experimental investigation on dynamic stiffening phenomenon[J]. Journal of Mechanics, 2004, 36(1): 118-124.(in Chinese) doi: 10.3321/j.issn:0459-1879.2004.01.019 [11] 杨辉, 洪嘉振. 刚-柔耦合多体系统动力学建模与数值仿真[J]. 计算力学学报, 2003, 20(4): 402-408. (YANG Hui, HONG Jiazhen. Dynamic modeling and numerical simulation of rigid flexible coupling multibody system[J]. Journal of Computational Mechanics, 2003, 20(4): 402-408.(in Chinese) doi: 10.3969/j.issn.1007-4708.2003.04.004 [12] 洪嘉振, 蒋丽忠. 动力刚化与多体系统刚-柔耦合动力学[J]. 计算力学学报, 1999, 16(3): 44-50. (HONG Jiazhen, JIANG Lizhong. Dynamic stiffening and multibody dynamics with coupled rigid and deformation motions[J]. Chinese Journal of Computational Mechanics, 1999, 16(3): 44-50.(in Chinese) [13] 蔡国平, 洪嘉振. 中心刚体-柔性悬臂梁系统的动力特性研究[J]. 航空学报, 2004, 25(3): 248-253. (CAI Guoping, HONG Jiazhen. Dynamic characteristics of the central rigid flexible cantilever system[J]. Acta Aeronautica et Astronautica Sinica, 2004, 25(3): 248-253.(in Chinese) doi: 10.3321/j.issn:1000-6893.2004.03.010 [14] 蔡国平, 李琳, 洪嘉振. 中心刚体-柔性梁系统的最优跟踪控制[J]. 力学学报, 2006, 38(1): 97-105. (CAI Guoping, LI Lin, HONG Jiazhen. Optimal tracking control of central rigid body flexible beam system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 97-105.(in Chinese) doi: 10.3321/j.issn:0459-1879.2006.01.013 [15] HAO D, WEI C. Dynamic characteristics analysis of bi-directional functionally graded Timoshenko beams[J]. Composite Structures, 2016, 141: 253-263. doi: 10.1016/j.compstruct.2016.01.051 [16] BANERJEE J R. Dynamic stiffness formulation and free vibration analysis of centrifugally stiffened Timoshenko beams[J]. Journal of Sound and Vibration, 2001, 247(1): 97-115. doi: 10.1006/jsvi.2001.3716 [17] YOU C, HONG J, CAI G. Modeling study of a flexible hub-beam system with large motion and with considering the effect of shear deformation[J]. Journal of Sound and Vibration, 2006, 295(1/2): 282-293. [18] 陈镕, 万春风, 薛松涛, 等. Timoshenko梁运动方程的修正及其影响[J]. 同济大学学报 (自然科学版), 2005, 33(6): 711-715. (CHEN Rong, WAN Chunfeng, XUE Songtao, et al. Modification of motion equation of Timoshenko beam and its effect[J]. Journal of Tongji University (Natural Science Edition) , 2005, 33(6): 711-715.(in Chinese) [19] 边东洋. 铁木辛柯梁理论的缺陷及运动方程的修正[D]. 硕士学位论文. 上海: 同济大学, 2008.BIAN Dongyang. Defect of Timoshenko beam theory and correction of motion equation[D]. Master Thesis. Shanghai: Tongji University, 2008. (in Chinese) [20] 陕晋军, 刘暾, 齐乃明, 等. 再谈一类挠性结构的约束及非约束模态解法[J]. 中国空间科学技术, 2001, 21(6): 16-22. (SHAN Jinjun, LIU Tun, QI Naiming, et al. Re-discuss the solution of constrained and unconstrained mode for a kind of flexible structure[J]. Chinese Space Science and Technology, 2001, 21(6): 16-22.(in Chinese) [21] LOW K H, LAU M W S. Experimental investigation of the boundary condition of slewing beams using a high-speed camera system[J]. Mechanism and Machine Theory, 1995, 30(4): 629-643. doi: 10.1016/0094-114X(94)00058-S [22] XIAO S, DU Q, CHEN B, et al. Modal test and analysis of cantilever beam with tip mass[J]. Acta Mechanica Sinica, 2002, 18(4): 407-413. doi: 10.1007/BF02487792 [23] BANERJEE J R. Free vibration of centrifugally stiffened uniform and tapered beams using the dynamic stiffness method[J]. Journal of Sound and Vibration, 2000, 233(5): 857-875. doi: 10.1006/jsvi.1999.2855 [24] JENSEN J J. On the shear coefficient in Timoshenko’s beam theory[J]. Journal of Applied Mechanics, 1966, 33(2): 621-635. [25] STEPHEN N G. The second frequency spectrum of Timoshenko beams[J]. Journal of Sound and Vibration, 1981, 76(3): 578-582. [26] NESTERENKO V V. A theory for transverse vibrations of the Timoshenko beam[J]. Journal of Applied Mathematics and Mechanics, 1993, 57(4): 669-677. doi: 10.1016/0021-8928(93)90036-L [27] NAGULESWARAN S. Lateral vibration of a centrifugally tensioned uniform Euler-Bernoulli beam[J]. Journal of Sound and Vibration, 1994, 176(5): 613-624. doi: 10.1006/jsvi.1994.1402 [28] DU H, LIM M K, LIEW K M. A power series solution for vibration of a rotating Timoshenko beam[J]. Journal of Sound and Vibration, 1994, 175(4): 505-523. doi: 10.1006/jsvi.1994.1342 -




 下载:
下载:







 渝公网安备50010802005915号
渝公网安备50010802005915号