Structure-Preserving Layout Optimization of Precision Devices in Spacecraft
-
摘要:
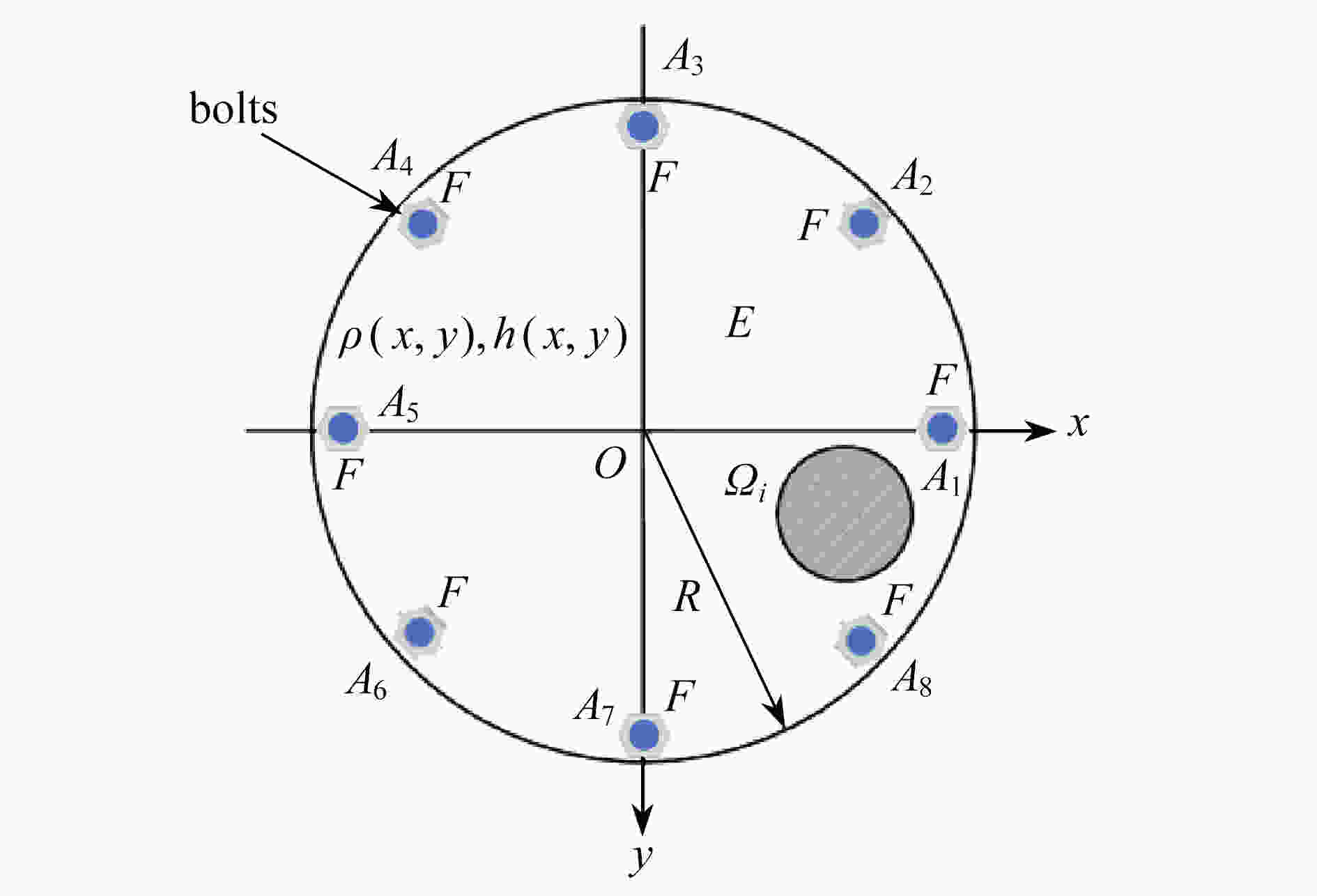
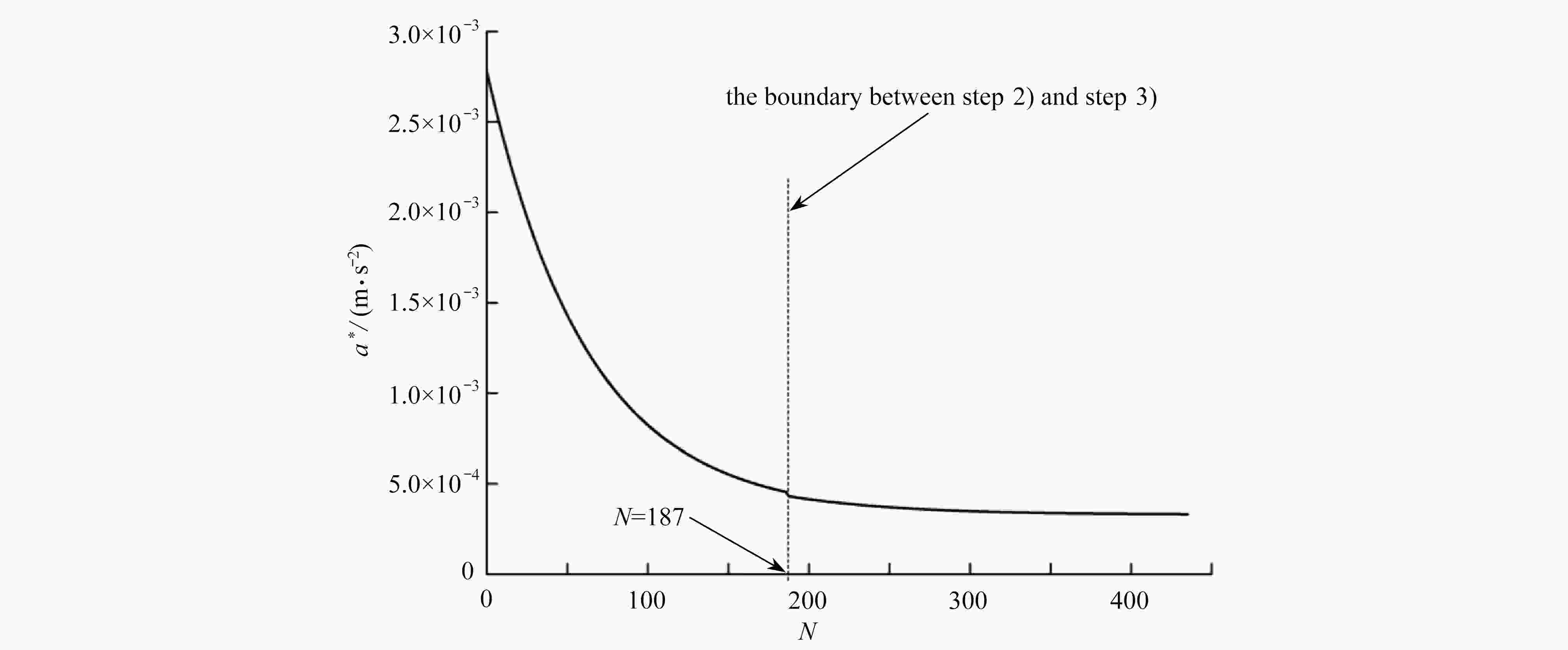
航天器中精密器件的稳定性和工作精度决定于器件布置位置的局部结构振动特性,而航天器局部振动特性又受到精密器件布局的影响。因此,航天器中精密器件的布局优化是确保其稳定高效工作的前提条件。该文建立了粘接精密器件的航天器局部柔性薄板结构的动力学模型,发展保结构分析方法模拟了薄板结构的局部振动特性。考虑精密器件形状和尺寸、散热间隙要求等布局约束条件,以各器件布局位置最大面外振动加速度加权值最小化为优化目标,对精密器件布局进行优化设计。优化结果表明:由于所提出的精密器件布局优化设计方法在模拟结构局部振动特性过程中采用了能够较为精确捕捉系统局部动力学特性的保结构分析方法,大幅提高优化效率的同时能够大幅降低器件布局位置最大面外振动加速度;通过布局优化设计,各器件布局位置最大面外振动加速度加权值减小约88.05%,这一结果对提高航天器内精密器件工作稳定性和精度具有一定的参考价值。
Abstract:The stability and the accuracy of the precision devices installed in spacecraft depend on the local vibration characteristics of the spacecraft. In return, the local vibration characteristics of the spacecraft are influenced by the layout of the precision devices, which implies that, a rational layout of the precision devices in the spacecraft is the precondition for the stable and efficient work of the precision devices. The dynamic model for a flexible panel bearing several precision devices was presented and the structure-preserving method was developed to investigate the local vibration characteristics of the panel. In view of the sizes of the precision devices and the heat dissipation clearances between the precision devices, the layout optimization for the precision devices was performed to minimize the weighted values of the out-of-plane vibration accelerations of the precision devices. The optimization results show that, benefiting from the excellent structure-preserving properties of the numerical method employed during the vibration analysis, the weighted values of the out-of-plane vibration accelerations of the precision devices decrease by about 88.05% through the layout optimization, which provides a useful guide for the layout scheme of the precision devices in the spacecraft and improves the stability of the precision devices.
-
-
[1] CARTMELL M P, MCKENZIE D J. A review of space tether research[J]. Progress in Aerospace Sciences, 2008, 44(1): 1-21. doi: 10.1016/j.paerosci.2007.08.002 [2] LIU J F, HAO L, LI G, et al. Multi-objective layout optimization of a satellite module using the Wang-Landau sampling method with local search[J]. Frontiers of Information Technology & Electronic Engineering, 2016, 17(6): 527-542. [3] CURTY CUCO A P, DE SOUSA F L, SILVA NETO A J. A multi-objective methodology for spacecraft equipment layouts[J]. Optimization and Engineering, 2015, 16(1): 165-181. doi: 10.1007/s11081-014-9252-z [4] RUMERMAN M L. Vibration and wave-propagation in ribbed plates[J]. Journal of the Acoustical Society of America, 1975, 57(2): 370-373. doi: 10.1121/1.380450 [5] ORRENIUS U, FINNVEDEN S. Calculation of wave propagation in rib-stiffened plate structures[J]. Journal of Sound and Vibration, 1996, 198(2): 203-224. doi: 10.1006/jsvi.1996.0565 [6] ICHCHOU M N, BERTHAUT J, COLLET M. Multi-mode wave propagation in ribbed plates, part Ⅰ: wavenumber-space characteristics[J]. International Journal of Solids and Structures, 2008, 45(5): 1179-1195. doi: 10.1016/j.ijsolstr.2007.09.032 [7] ICHCHOU M N, BERTHAUT J, COLLET M. Multi-mode wave propagation in ribbed plates, part Ⅱ: predictions and comparisons[J]. International Journal of Solids and Structures, 2008, 45(5): 1196-1216. doi: 10.1016/j.ijsolstr.2007.08.020 [8] 郑明亮, 刘洁, 邓斌. 覆冰输电导线舞动的Noether对称性和守恒量[J]. 应用数学和力学, 2021, 42(3): 275-281. (ZHENG Mingliang, LIU Jie, DENG Bin. The Noether symmetry and conserved quantity of galloping iced power transmission lines[J]. Applied Mathematics and Mechanics, 2021, 42(3): 275-281.(in Chinese) [9] 满淑敏, 高强, 钟万勰. 非完整约束Hamilton动力系统保结构算法[J]. 应用数学和力学, 2020, 41(6): 581-590. (MAN Shumin, GAO Qiang, ZHONG Wanxie. A structure-preserving algorithm for Hamiltonian systems with nonholonomic constraints[J]. Applied Mathematics and Mechanics, 2020, 41(6): 581-590.(in Chinese) [10] 刘晓梅, 周钢, 朱帅. Hamilton系统下基于相位误差的精细辛算法[J]. 应用数学和力学, 2019, 40(6): 595-608. (LIU Xiaomei, ZHOU Gang, ZHU Shuai. A highly precise symplectic direct integration method based on phase errors for Hamiltonian systems[J]. Applied Mathematics and Mechanics, 2019, 40(6): 595-608.(in Chinese) [11] HU W P, WANG Z, ZHAO Y P, et al. Symmetry breaking of infinite-dimensional dynamic system[J]. Applied Mathematics Letters, 2020, 103: 106207. doi: 10.1016/j.aml.2019.106207 [12] HU W P, DENG Z C, HAN S M, et al. Generalized multi-symplectic integrators for a class of Hamiltonian nonlinear wave PDEs[J]. Journal of Computational Physics, 2013, 235: 394-406. doi: 10.1016/j.jcp.2012.10.032 [13] HU W P, HUAI Y L, XU M B, et al. Mechanoelectrical flexible hub-beam model of ionic-type solvent-free nanofluids[J]. Mechanical Systems and Signal Processing, 2021, 159: 107833. doi: 10.1016/j.ymssp.2021.107833 [14] HU W P, ZHANG C Z, DENG Z C. Vibration and elastic wave propagation in spatial flexible damping panel attached to four special springs[J]. Communications in Nonlinear Science and Numerical Simulation, 2020, 84: 105199. doi: 10.1016/j.cnsns.2020.105199 [15] HU W P, YE J, DENG Z C. Internal resonance of a flexible beam in a spatial tethered system[J]. Journal of Sound and Vibration, 2020, 475: 115286. doi: 10.1016/j.jsv.2020.115286 [16] ZHAO P F, QIN M Z. Multisymplectic geometry and multisymplectic Preissmann scheme for the KdV equation[J]. Journal of Physics A: Mathematical and General, 2000, 33(18): 3613-3626. doi: 10.1088/0305-4470/33/18/308 [17] PREISSMANN A. Propagation des intumescences dans les canaux et rivieres[C]//First Congress French Association for Computation. Grenoble, France, 1961: 433-442. -





 下载:
下载:


 渝公网安备50010802005915号
渝公网安备50010802005915号