Active Control on Band Gap Properties and Interface Transmission of Elastic Waves in Piezoelectric Metamaterial Beams
-
摘要:
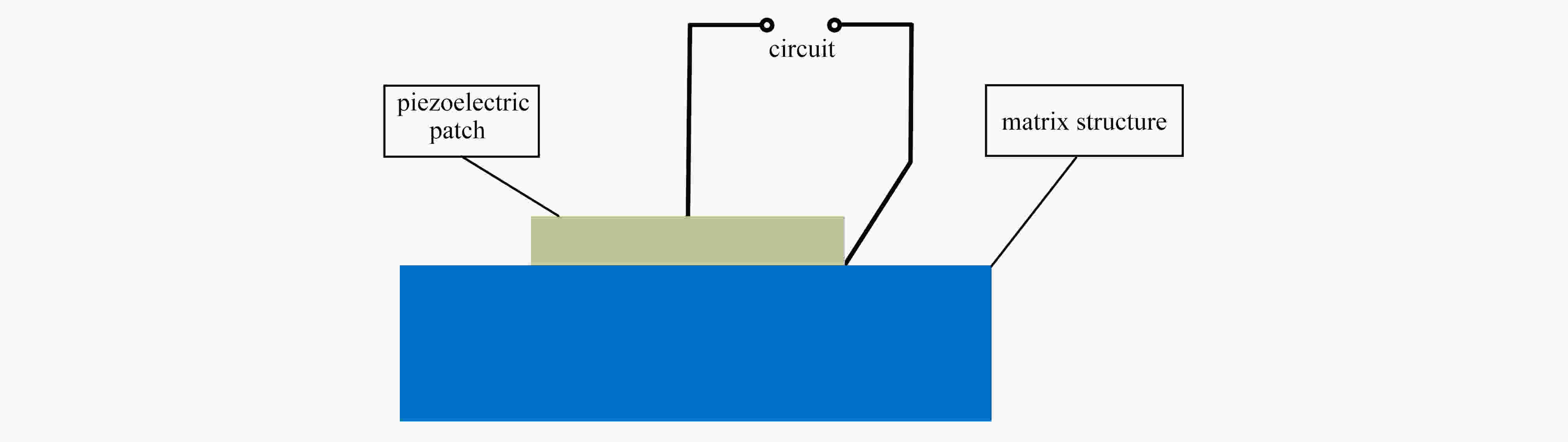
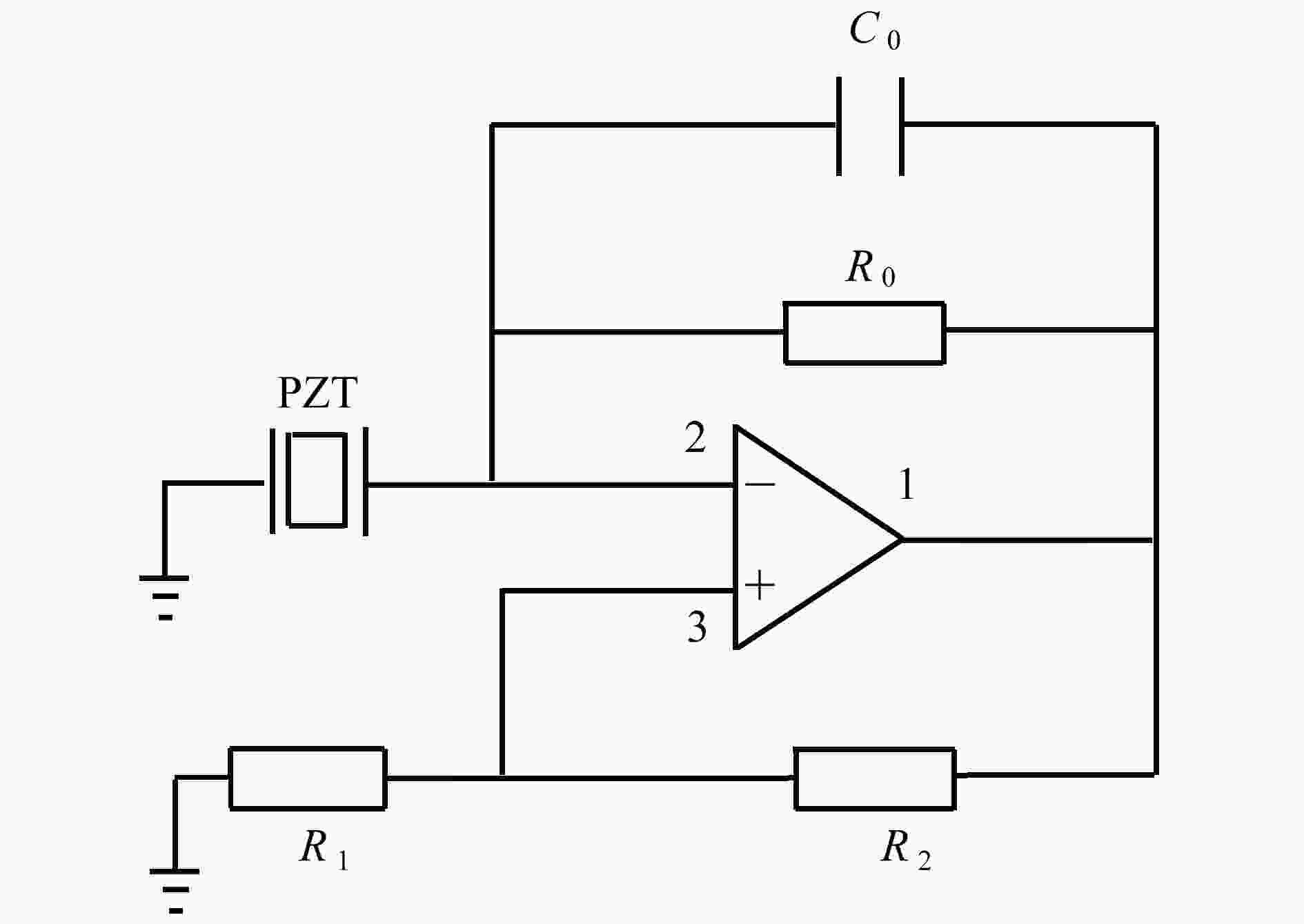
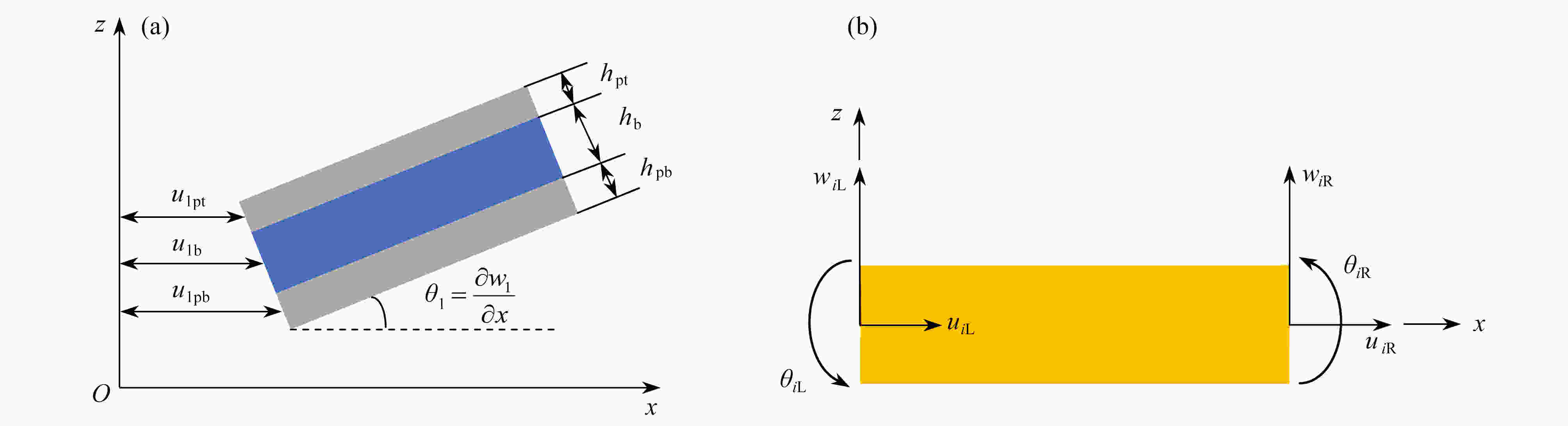
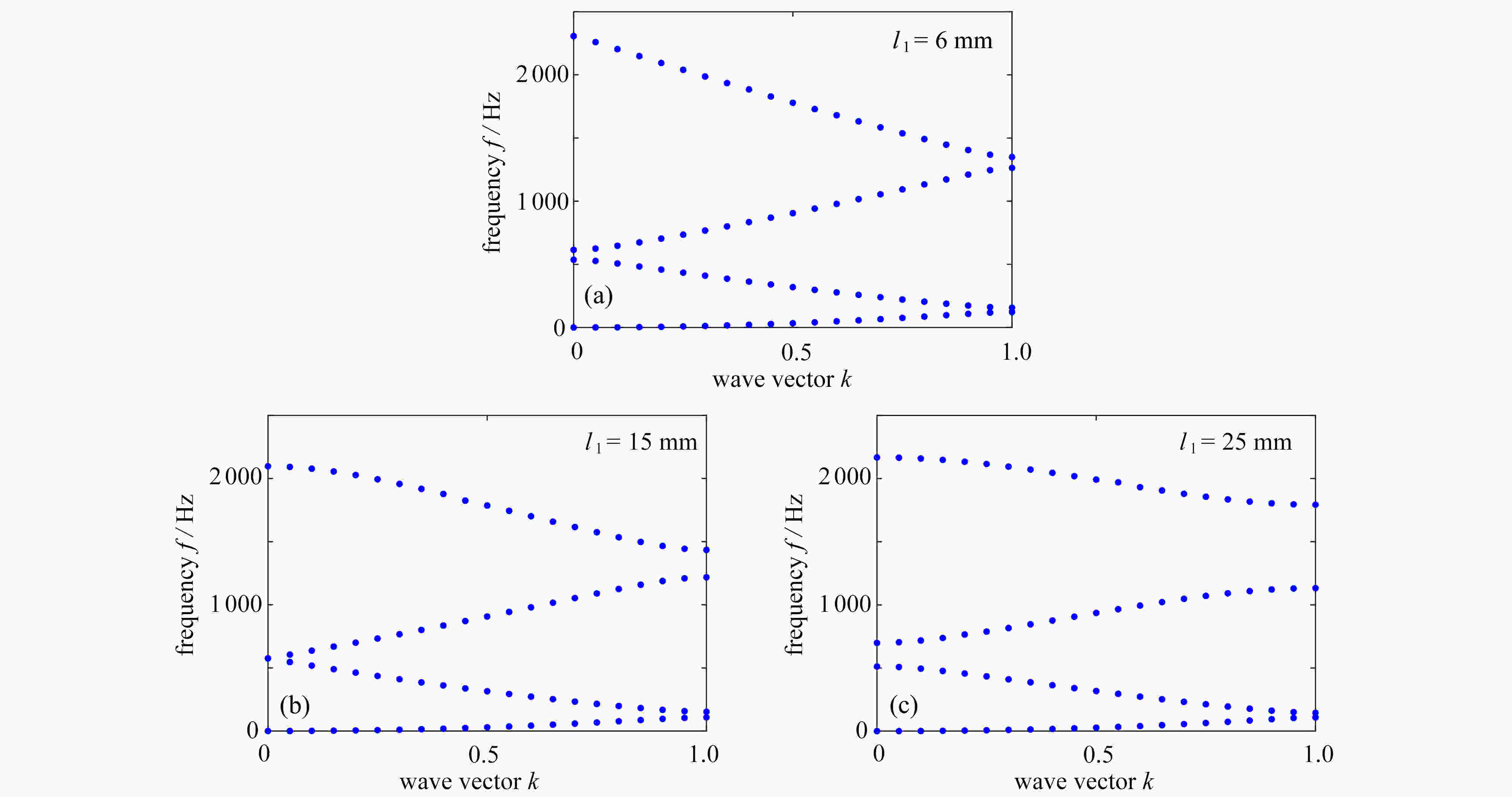
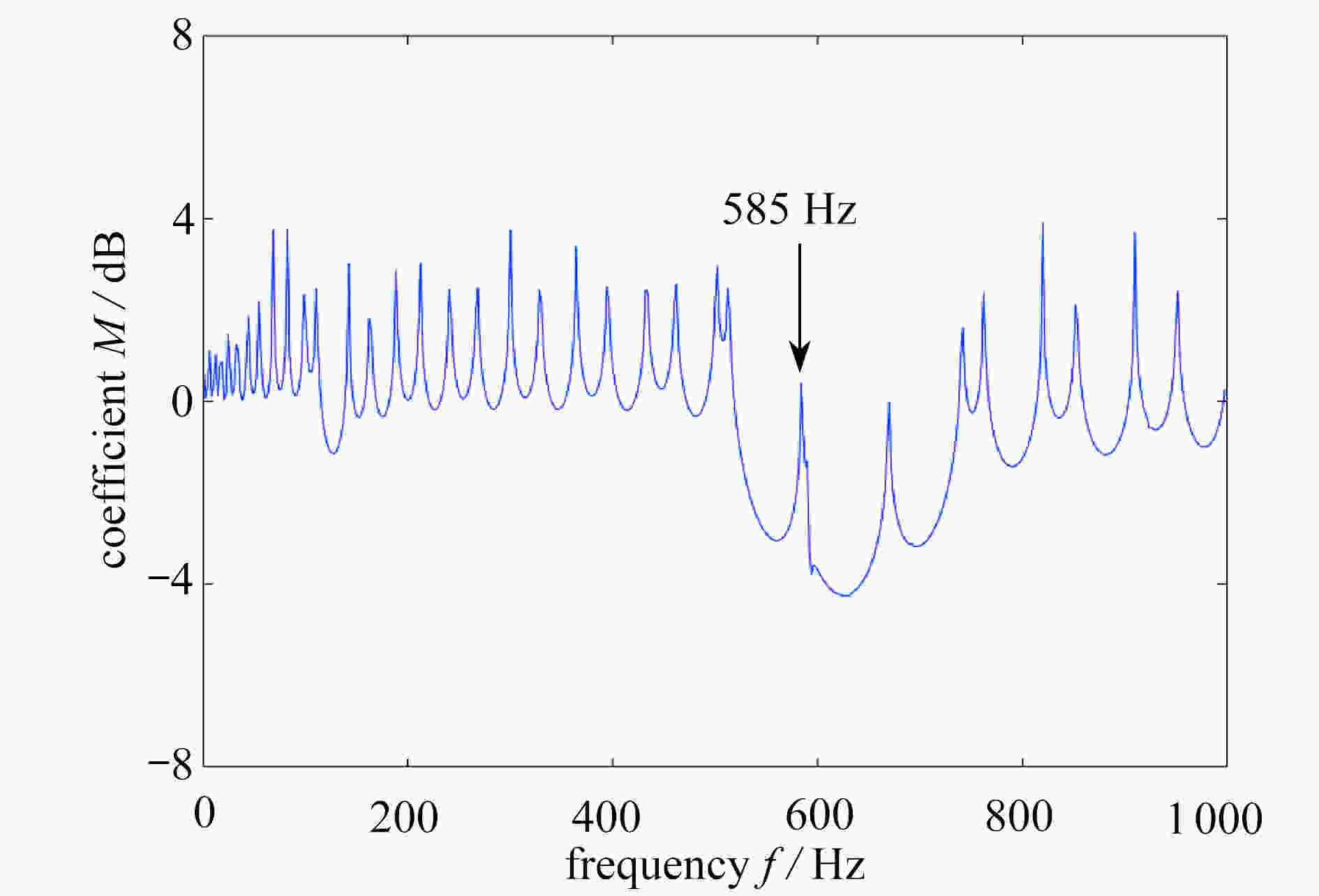
该文采用周期压电负电容电路，研究了弹性波超材料梁中带隙特性的主动控制问题。该系统利用外部电路改变所连接压电材料的材料参数，从而改变结构的等效参数，实现对带隙特性的调控。通过对单胞进行控制，可观察到主动控制系统作用时带隙的产生与消失。构造了含有交界面的弹性波超材料梁结构，分析了主动控制系统对波动界面传输特性的影响。
Abstract:The active control on band gap properties of elastic wave metamaterial beams was studied by means of the negative capacitance circuits attached to piezoelectric sheets periodically. External circuits were used to change the material constants of the connected piezoelectric materials, which could tune the equivalent parameters of the structure and control the band gap characteristics. Through controlling the unit cell, the generation and disappearance of band gaps can be observed with the active control system. Then, an elastic wave metamaterial beam with the interface was constructed to discuss the effects of the active control system on the interface transmission.
-
图 2 具有不等厚度压电片的主动弹性波超材料梁
Figure 2. Active elastic wave metamaterial beam attached by piezoelectric patches with different thicknesses
图 3 含有负电容电路的主动控制系统
Figure 3. The active control system with a negative capacitance circuit
图 4 变形关系：(a)超材料梁的变形；(b)节点的位移
Figure 4. The deformation relation: (a) the deformation of the layered elastic-piezoelectric beam; (b) the displacements of the nodes
图 5 压电片对称粘贴但厚度改变时弹性波超材料梁的局部化因子
Figure 5. The localization factors of the elastic metamaterial beam with different-thickness piezoelectric sheets symmetrically pasted
图 6 上下层压电片厚度相同与不同时弹性波超材料梁的局部化因子
Figure 6. The localization factors of the elastic metamaterial beam with the same- and different-thickness piezoelectric patches
图 7 弹性波超材料梁有无主动控制时的局部化因子
Figure 7. The localization factors of the elastic metamaterial beam with and without active control
图 8 实验装置：(a)数据采集仪（上）和信号放大器（下）；(b)信号发生器；(c)实验模型；(d)电路实物图；(e)压电片细节图
Figure 8. The experimental equipment: (a) the data acquisition instrument (upper) and the signal amplifier (lower); (b) the signal generator; (c) the experimental model; (d) the physical circuit diagram; (e) the detailed diagram of the piezoelectric patch
图 9 传输响应：(a) 3 850 Hz，主动控制前；(b) 3 850 Hz，主动控制后；(c) 5 659 Hz，主动控制前；(d) 5 659 Hz，主动控制后
Figure 9. Transmission responses: (a) at 3 850 Hz before active control (b) at 3 850 Hz after active control; (c) at 5 659 Hz before active control; (d) at 5 659 Hz after active control
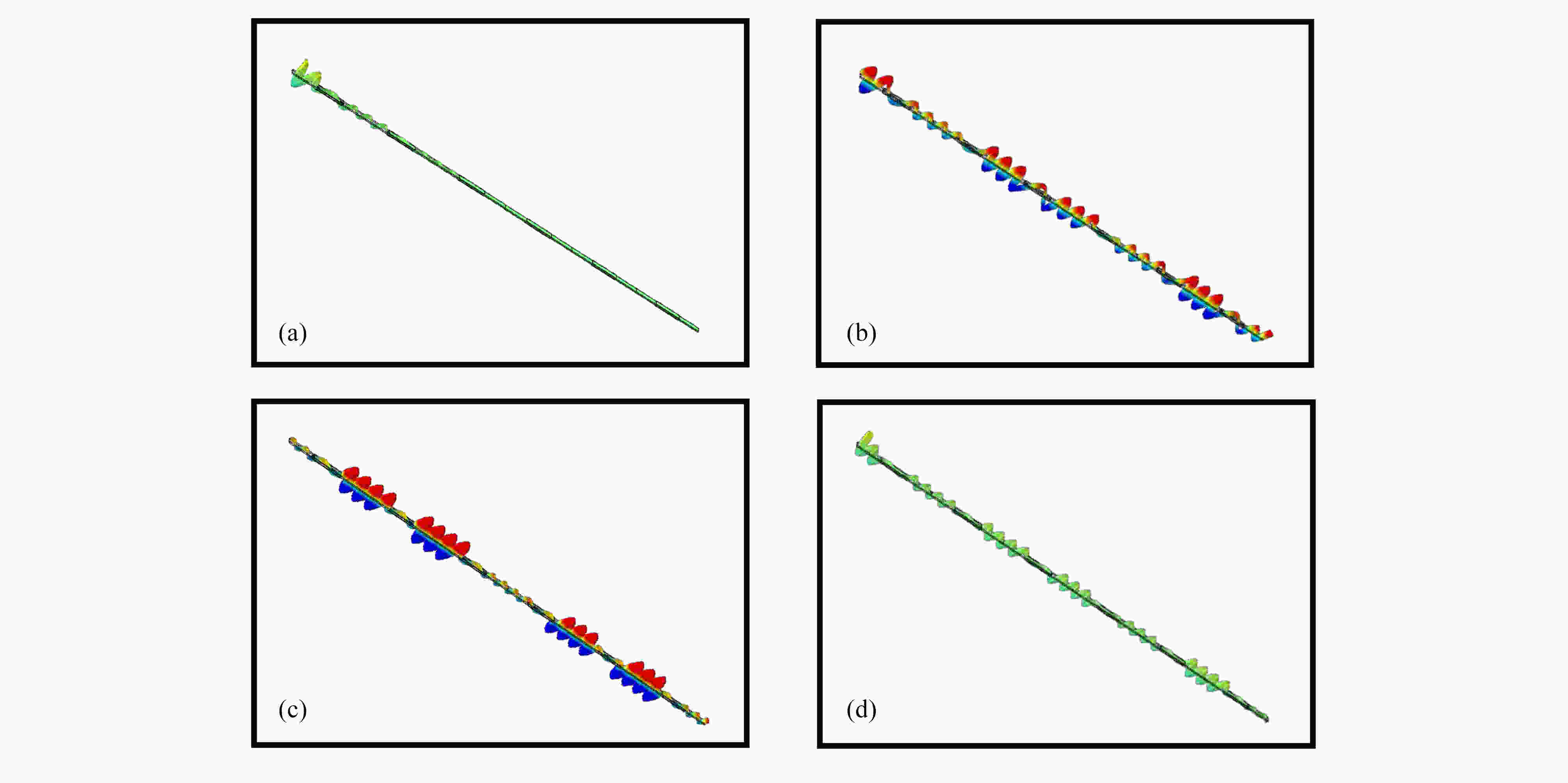
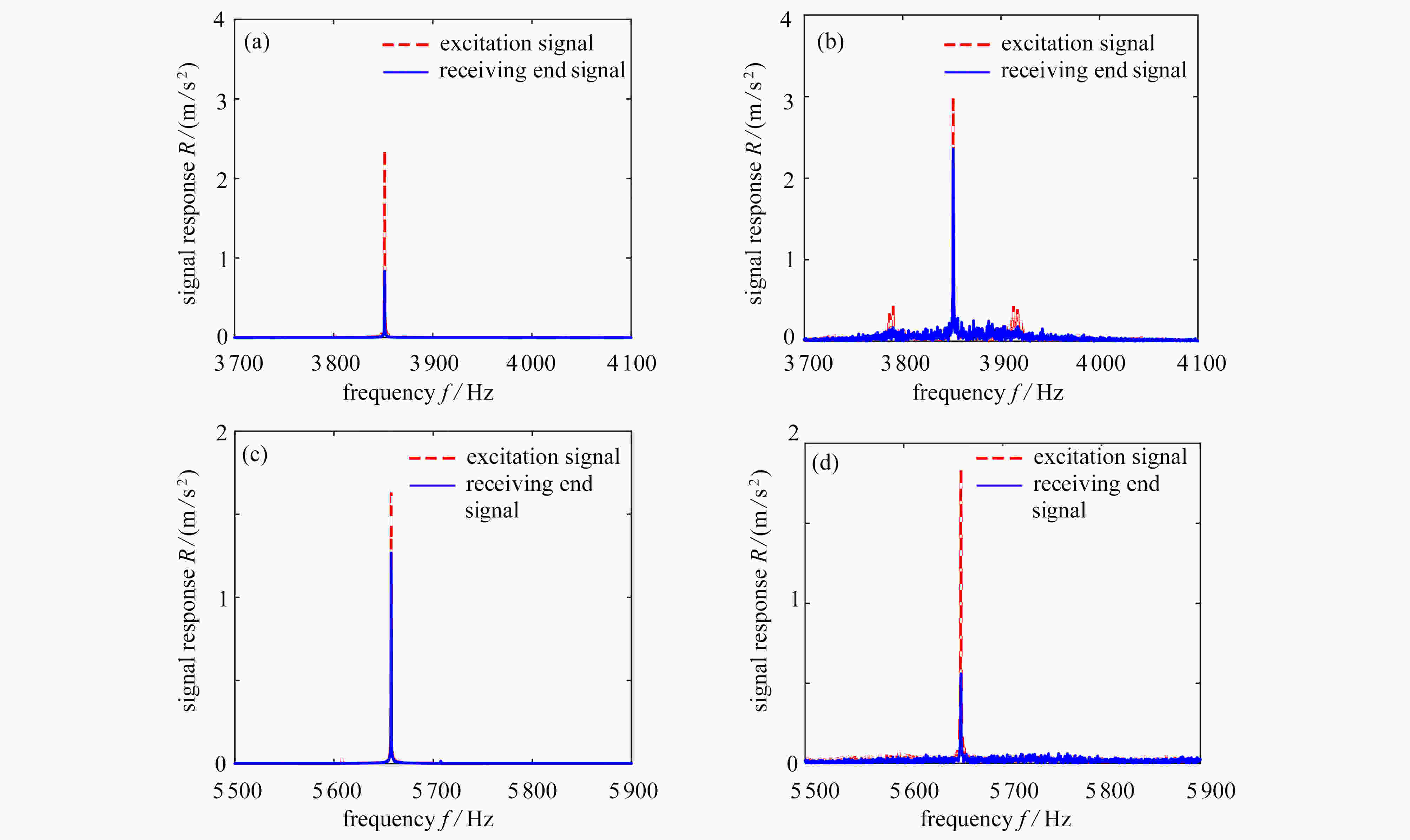
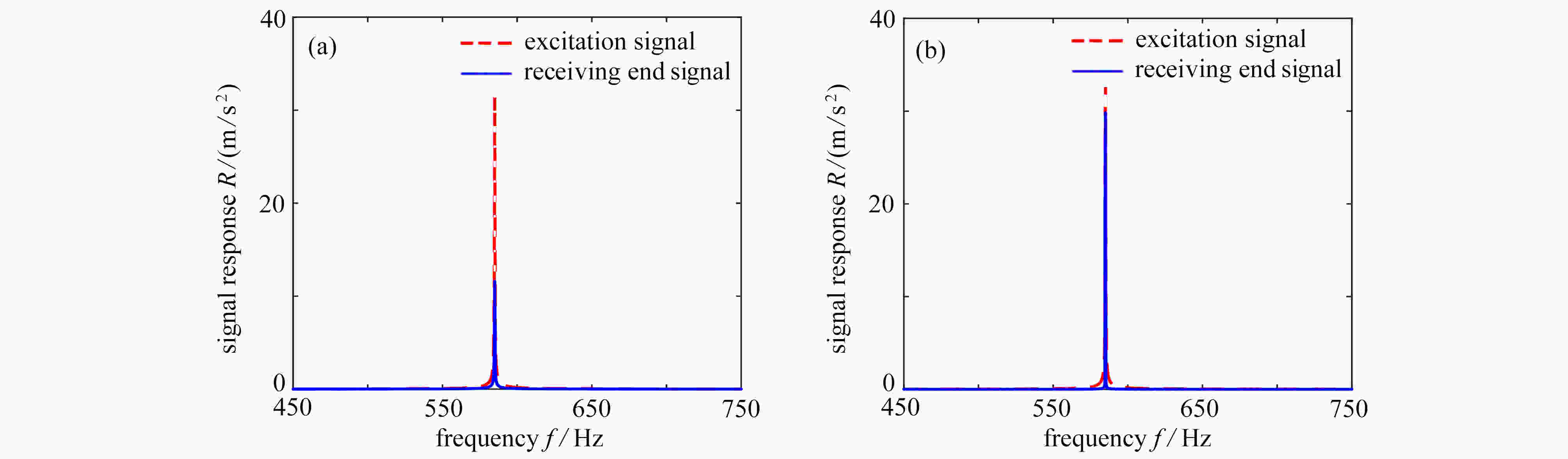
图 10 激励端和接收端的响应值：(a) 3 850 Hz，主动控制前；(b) 3 850 Hz, 主动控制后；(c) 5 659 Hz，主动控制前；(d) 5 659 Hz，主动控制后
Figure 10. The responses at the excitation and the receiving end: (a) at 3 850 Hz, before active control; (b) at 3 850 Hz, after active control; (c) at 5 659 Hz, before active control; (d) at 5 659 Hz, after active control
-
[1] 陈启勇, 胡少伟, 张子明. 基于声子晶体理论的弹性地基梁的振动特性研究[J]. 应用数学和力学, 2014, 35(1): 29-38. (CHEN Qiyong, HU Shaowei, ZHANG Ziming. Research on the vibration property of the beam on elastic foundation based on the PCs theory[J]. Applied Mathematics and Mechanics, 2014, 35(1): 29-38.(in Chinese) doi: 10.3879/j.issn.1000-0887.2014.01.004 [2] 贠昊, 邓子辰, 朱志韦. 弹性波在星形节点周期结构蜂窝材料中的传播特性研究[J]. 应用数学和力学, 2015, 36(8): 814-820. (YUN Hao, DENG Zichen, ZHU Zhiwei. Bandgap properties of periodic 4-point star-shaped honeycomb materials with negative Poisson’s ratios[J]. Applied Mathematics and Mechanics, 2015, 36(8): 814-820.(in Chinese) doi: 10.3879/j.issn.1000-0887.2015.08.003 [3] SHI P, CHEN C Q, ZOU W N. Propagation of shear elastic and electromagnetic waves in one dimensional piezoelectric and piezomagnetic composites[J]. Ultrasonics, 2015, 55: 42-47. doi: 10.1016/j.ultras.2014.08.011 [4] 张宏宽, 周萧明. 声波超材料设计的力学原理与进展[J]. 固体力学学报, 2016, 37(5): 387-397. (ZHANG Hongkuan, ZHOU Xiaoming. Mechanics concepts and advances of acoustic metamaterials design[J]. Chinese Journal of Solid Mechanics, 2016, 37(5): 387-397.(in Chinese) [5] CHEN Y J, HUANG Y, LU C F, et al. A two-way unidirectional narrow-band acoustic filter realized by a graded phononic crystal[J]. Journal of Applied Mechanics: Transactions of the ASME, 2017, 84(9): 091003. doi: 10.1115/1.4037148 [6] NEJADSADEGHI N, PLACIDI L, ROMEO M, et al. A frequency band gaps in dielectric granular metamaterials modulated by electric field[J]. Mechanics Research Communications, 2019, 95: 96-103. doi: 10.1016/j.mechrescom.2019.01.006 [7] TANG L L, CHENG L, CHEN K. Complete sub-wavelength flexural wave band gaps in plates with periodic acoustic black holes[J]. Journal of Sound and Vibration, 2021, 502: 116102. doi: 10.1016/j.jsv.2021.116102 [8] CHEN J J, ZHANG K W, GAO J, et al. Stopbands for lower-order Lamb waves in one-dimensional composite thin plates[J]. Physical Review B, 2006, 73: 094307. doi: 10.1103/PhysRevB.73.094307 [9] WANG Y Z, LI F M, KISHIMOTO K, et al. Wave localization in randomly disordered layered three-component phononic crystals with thermal effects[J]. Archive of Applied Mechanics, 2010, 80: 629-640. doi: 10.1007/s00419-009-0329-7 [10] DING L, ZHU H P, YIN T. Wave propagation in a periodic elastic-piezoelectric axial-bending coupled beam[J]. Journal of Sound and Vibration, 2013, 332(24): 6377-6388. doi: 10.1016/j.jsv.2013.06.021 [11] MA T, CHEN T N, WANG X P, et al. Band structures of bilayer radial phononic crystal plate with crystal gliding[J]. Journal of Applied Physics, 2014, 116(10): 104505. doi: 10.1063/1.4895138 [12] CHENG Y, LIU X J, WU D J. Band structure of a phononic crystal plate in the form of a staggered-layer structure[J]. Journal of Applied Physics, 2011, 109: 064904. doi: 10.1063/1.3561864 [13] CHENG Y, LIU X J, WU D J. Band structures of phononic-crystal plates in the form of a sandwich-layered structure[J]. Journal of the Acoustical Society of America, 2011, 130: 2738-2745. doi: 10.1121/1.3641365 [14] TSAI M S, WANG K W. A coupled robust control/optimization approach for active-passive hybrid piezoelectric networks[J]. Smart Materials and Structures, 2002, 11: 389-395. doi: 10.1088/0964-1726/11/3/309 [15] CHEN Y Y, HU G K, HUANG G L. An adaptive metamaterial beam with hybrid shunting circuits for extremely broadband control of flexural waves[J]. Smart Materials and Structures, 2016, 25(10): 105036. doi: 10.1088/0964-1726/25/10/105036 [16] 李凤明, 汪越胜. 压电周期结构振动主动控制研究[J]. 振动工程学报, 2004, 17: 828-830. (LI Fengming, WANG Yuesheng. Study on active vibration control in periodic piezoelectric structures[J]. Journal of Vibration Engineering, 2004, 17: 828-830.(in Chinese) doi: 10.3969/j.issn.1004-4523.2004.z2.076 [17] 陈圣兵, 韩小云, 郁殿龙, 等. 不同压电分流电路对声子晶体梁带隙的影响[J]. 物理学报, 2010, 59(1): 387-392. (CHEN Shengbing, HAN Xiaoyun, YU Dianlong, et al. Influences of different types of piezoelectric shunting circuits on band gaps of phononic beam[J]. Acta Physica Sinica, 2010, 59(1): 387-392.(in Chinese) doi: 10.7498/aps.59.387 [18] CARDELLA D, CELLI P, GONELLA S. Manipulating waves by distilling frequencies: a tunable shunt-enabled rainbow trap[J]. Smart Materials and Structures, 2016, 25(8): 085017. doi: 10.1088/0964-1726/25/8/085017 [19] CHEN S B, WEN J H, YU D L, et al. Band gap control of phononic beam with negative capacitance piezoelectric shunt[J]. Chinese Physics B, 2011, 20(1): 014301. doi: 10.1088/1674-1056/20/1/014301 [20] AIROLDI L, RUZZENE M. Design of tunable acoustic metamaterials through periodic arrays of resonant shunted piezos[J]. New Journal of Physics, 2011, 13: 113010. doi: 10.1088/1367-2630/13/11/113010 [21] DAI L X, JIANG S, LIAN Z Y, et al. Locally resonant band gaps achieved by equal frequency shunting circuits of piezoelectric rings in a periodic circular plate[J]. Journal of Sound and Vibration, 2015, 337: 150-160. doi: 10.1016/j.jsv.2014.10.026 [22] RAO M S, NARAYANAN S. Active control of wave propagation in multi-span beams using distributed piezoelectric actuators and sensors[J]. Smart Materials and Structures, 2007, 16(6): 2577-2594. doi: 10.1088/0964-1726/16/6/062 [23] HAGOOD N W, VONFLOTOW A. Damping of structural vibrations with piezoelectric materials and passive electrical networks[J]. Journal of Sound and Vibration, 1991, 146(2): 243-268. doi: 10.1016/0022-460X(91)90762-9 [24] WANG G, CHEN S B. Large low-frequency vibration attenuation induced by arrays of piezoelectric patches shunted with amplifier-resonator feedback circuits[J]. Smart Materials and Structures, 2015, 25(1): 015004. [25] CHEN P, WANG Y Z, WANG Y S. Active control of flexural waves in a phononic crystal beam with staggered periodic properties[J]. Wave Motion, 2020, 93: 102481. doi: 10.1016/j.wavemoti.2019.102481 -
下载:
点击查看大图
计量
- 文章访问数: 779
- HTML全文浏览量: 309
- PDF下载量: 101
- 被引次数: 0
