Size-Dependent Effects of Micro-Nano Mindlin Plates Based on the Couple Stress Theory
-
摘要:
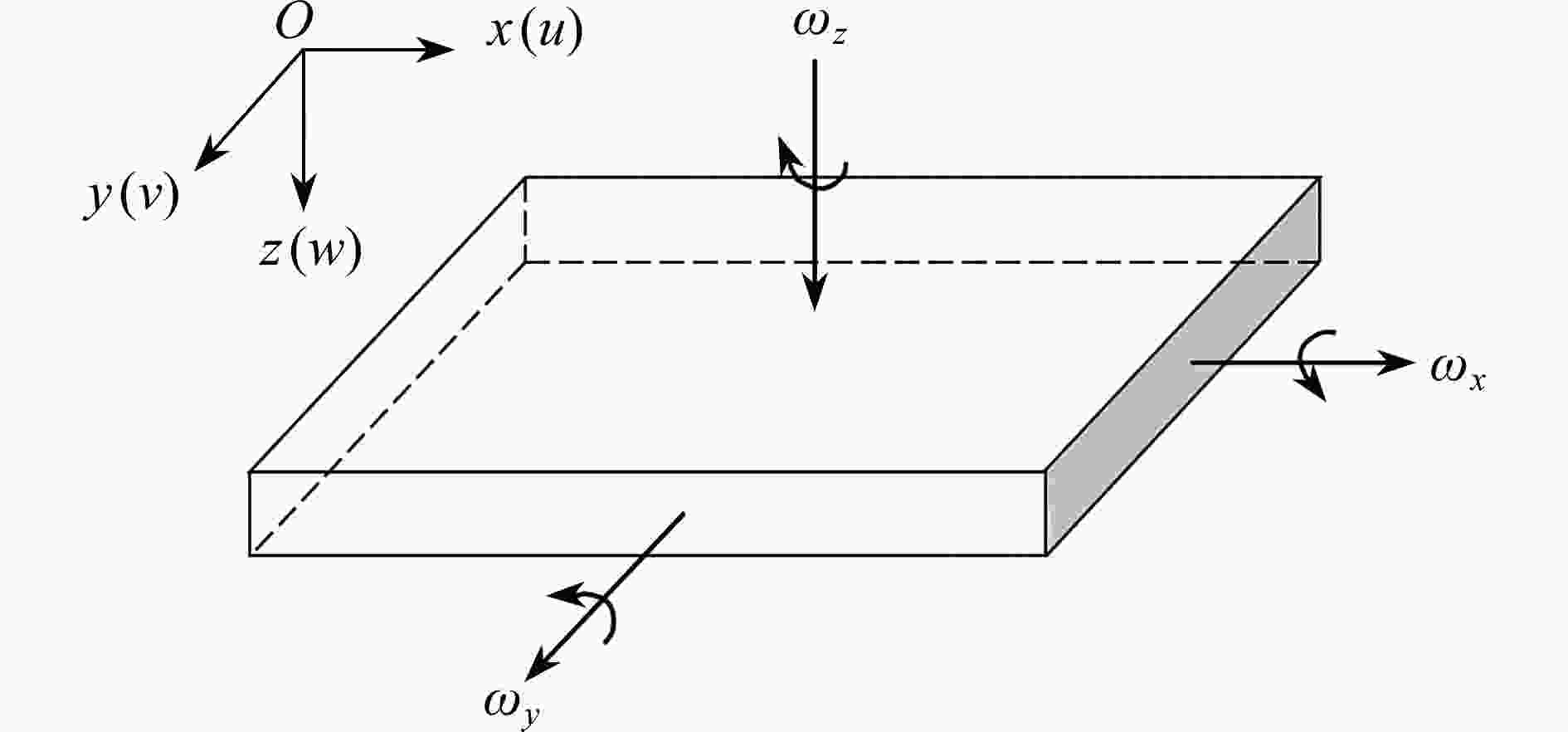
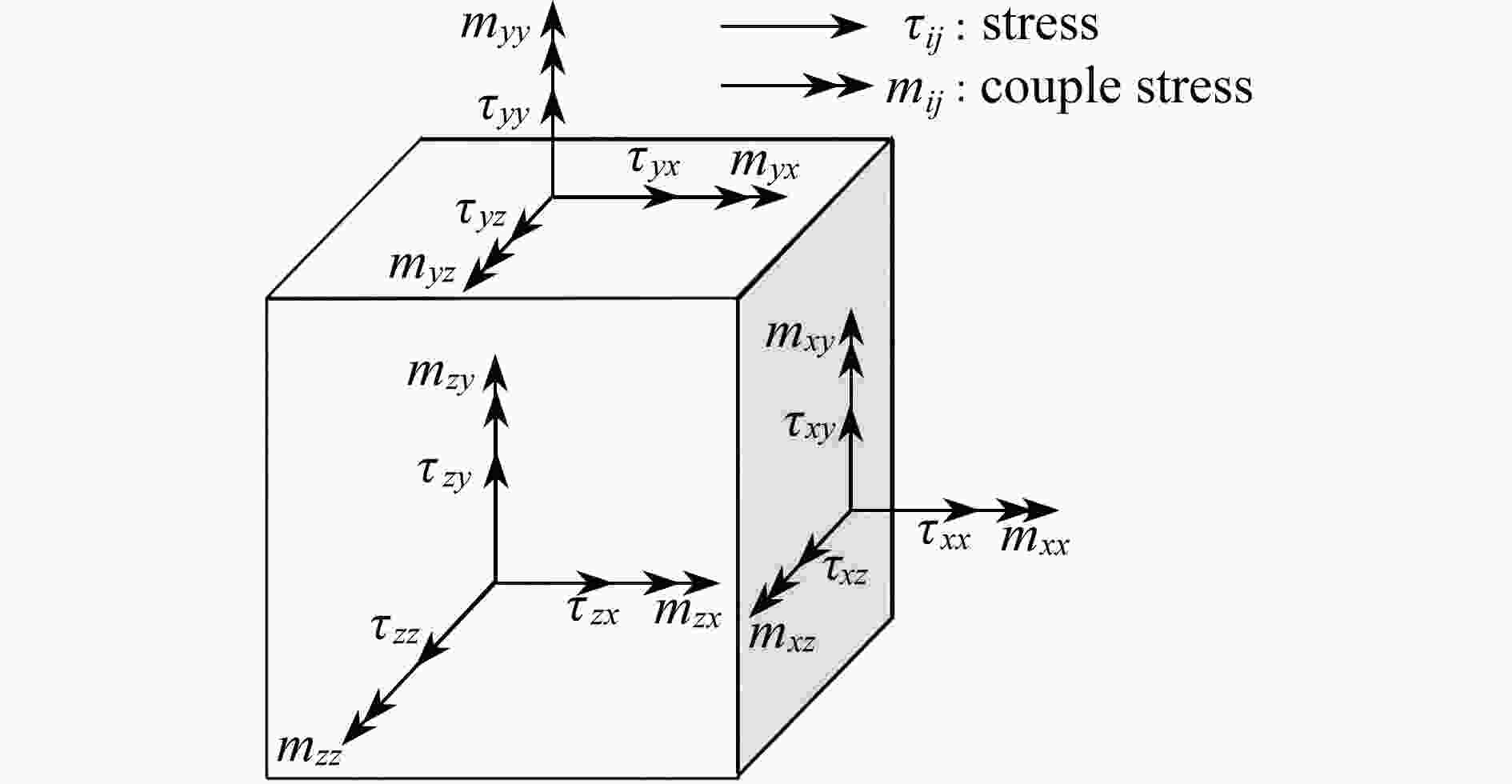
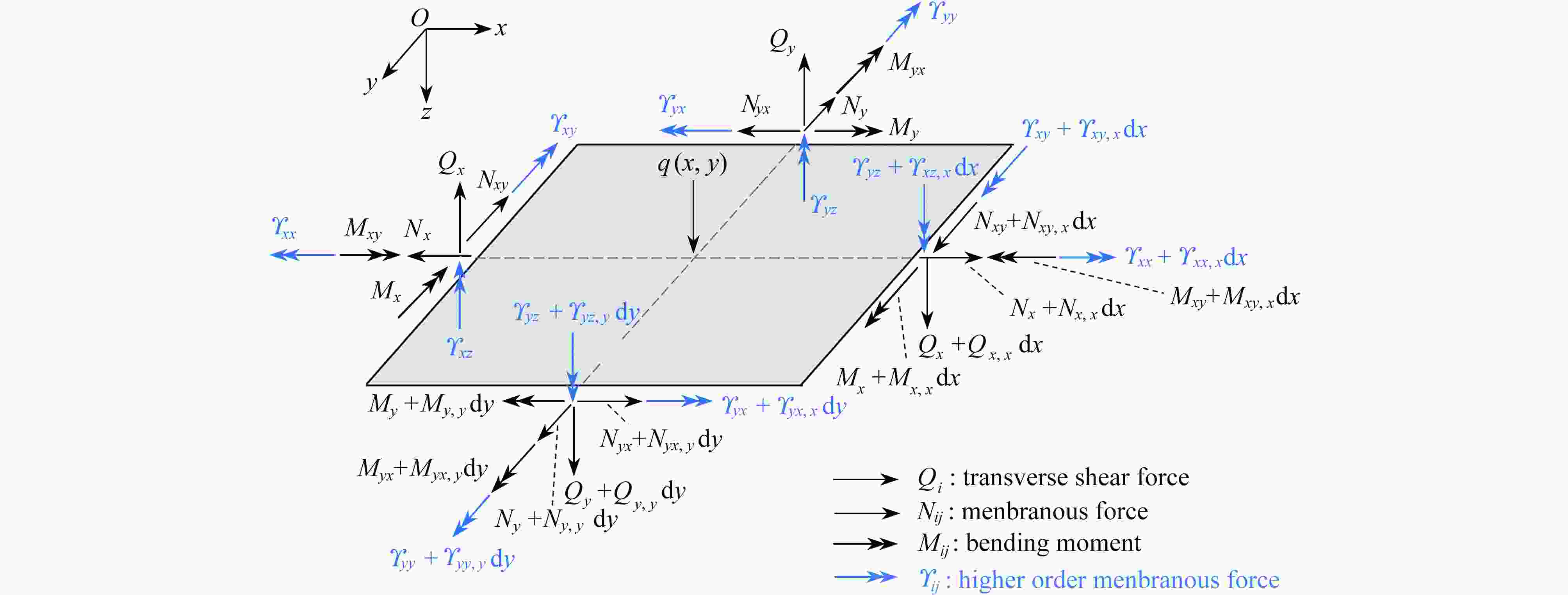
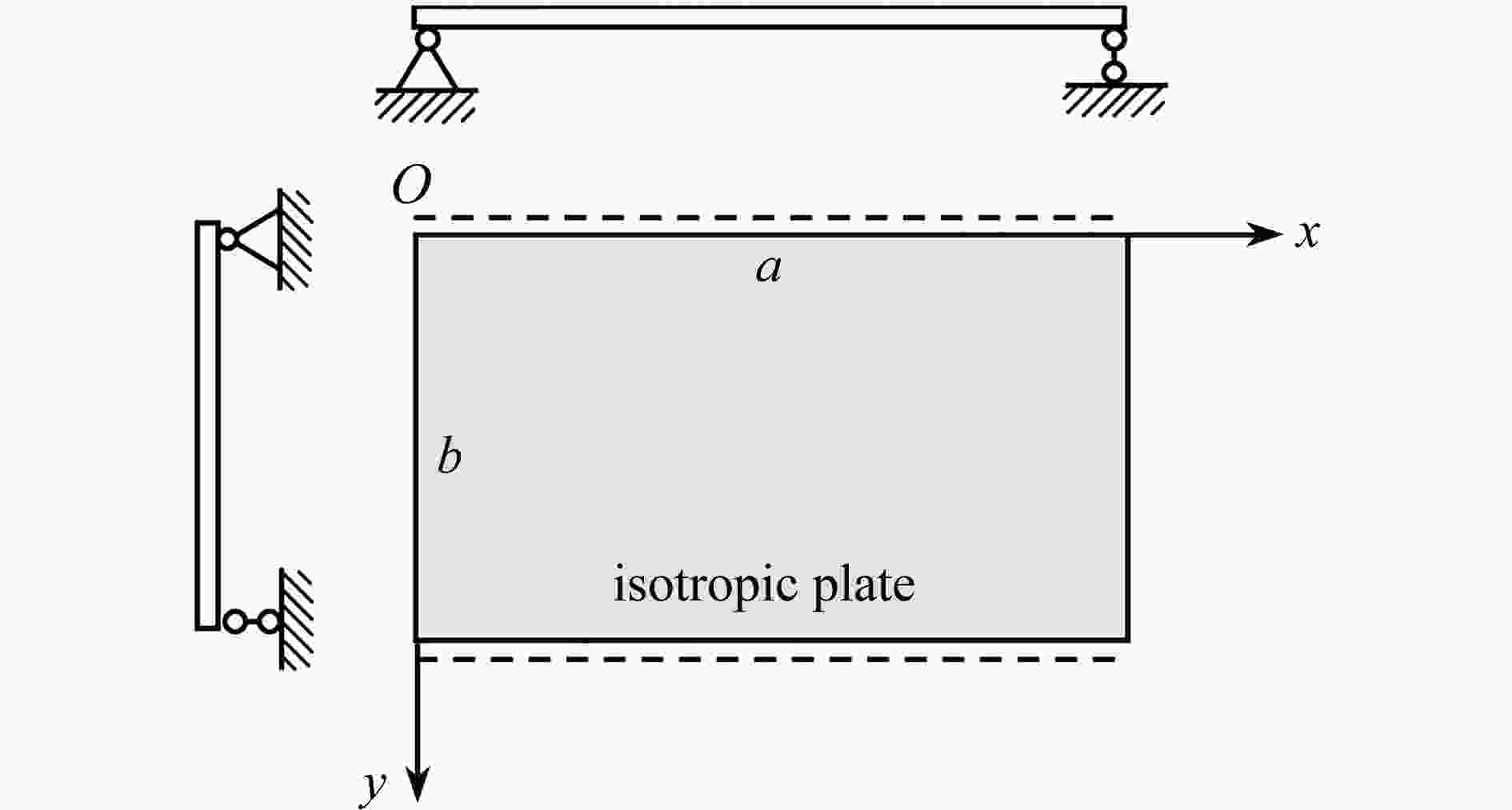
基于偶应力理论，建立了适用于微纳米结构的Mindlin板理论。考虑横向剪切变形和材料的尺度效应并引入长度尺寸参数，推导了各向同性微纳米Mindlin板的本构方程。根据板的平衡条件，进一步推导出用位移函数和转角函数表示的板的屈曲和振动控制方程。通过对位移和转角变量进行空间和时间域上的分离，得出了四边简支（SSSS）和对边简支、对边固支（SCSC）两种边界情况下微纳米板的屈曲和振动问题的解析解。然后利用MATLAB软件进行算例分析，获得了不同尺寸参数、长宽比、厚长比等情况下板的临界屈曲荷载和固有频率。研究结果与已有文献中的结果以及ABAQUS有限元仿真解进行对比，结果表明，不同参数下的三种方法得到的结果均十分接近。算例分析发现，尺度效应对屈曲载荷和固有频率都有显著影响。
-
关键词:
- 偶应力 /
- 尺度效应 /
- Mindlin板理论 /
- 屈曲 /
- 振动
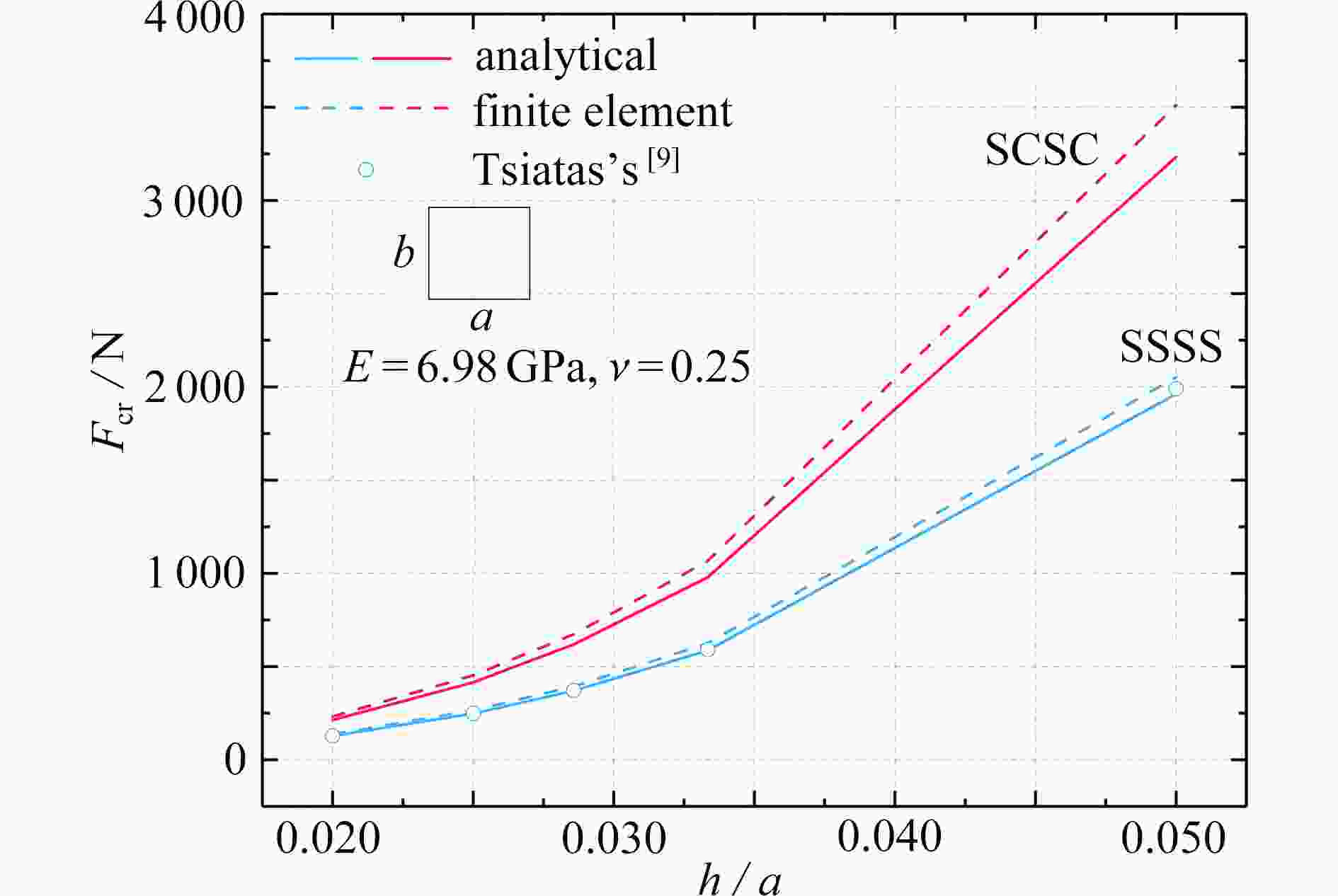
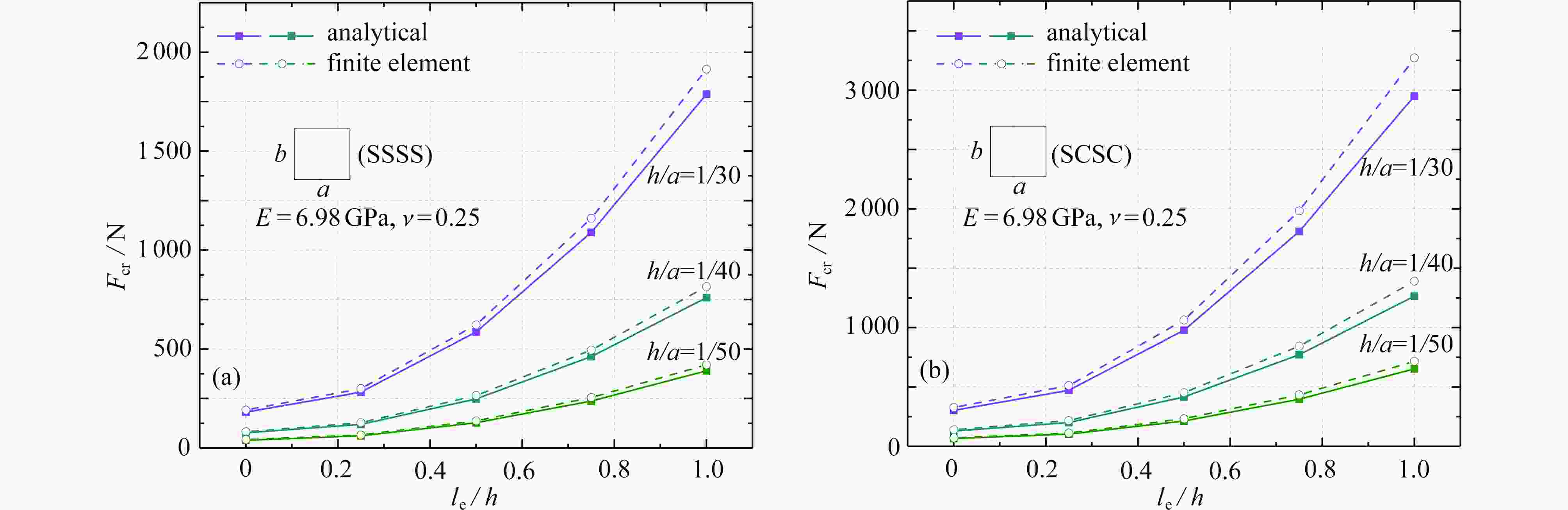
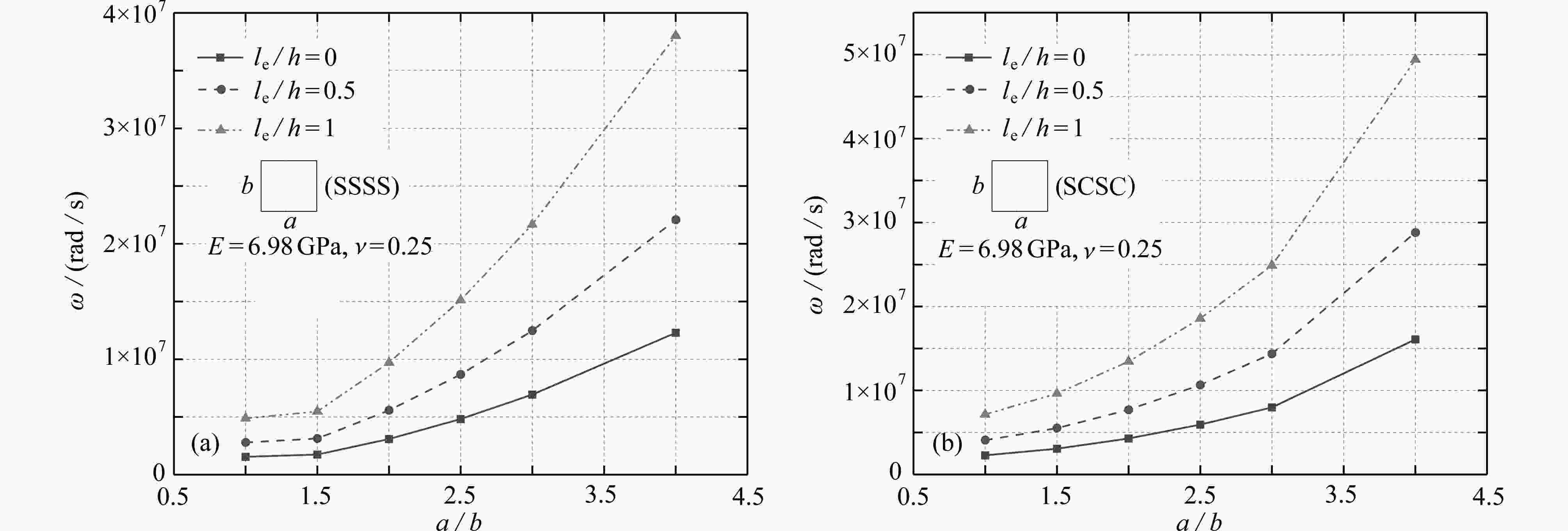
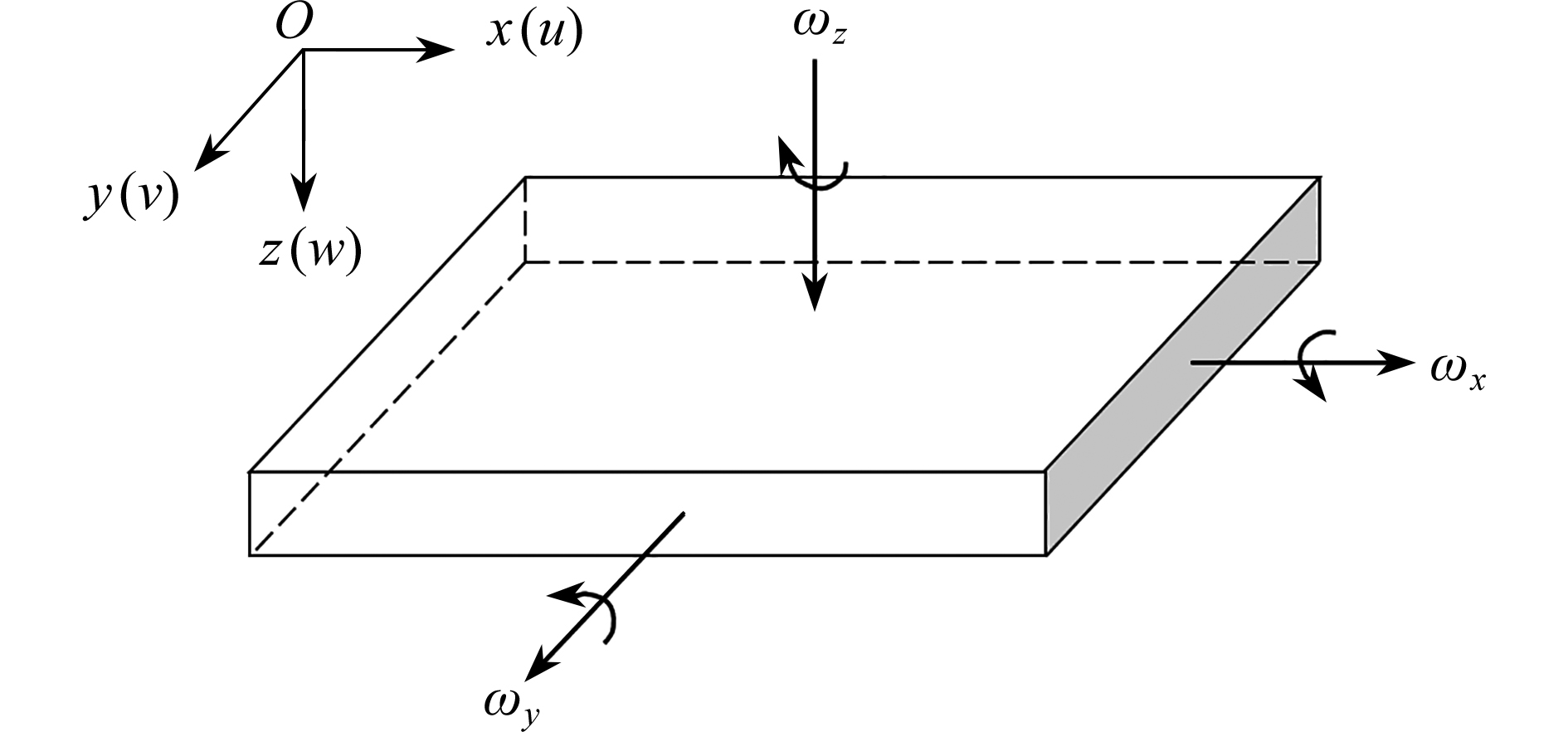
Abstract:A Mindlin plate theory for micro-nano structures was proposed based on the couple stress theory. A length parameter was introduced to consider the size effect, and the constitutive equations for the micro-nano Mindlin plate were derived in view of the transverse shear deformation. The buckling and free vibration governing equations in terms of displacements and the slope functions of the shear deformation micro-nano plate were further deduced with the force equilibrium conditions. The analytical solutions of buckling and free vibration for the shear deformation micro-nano plate were obtained through separation of the displacement and rotation variables in space and time domains. Two scenarios of boundary conditions were analyzed: SSSS (simply supported by 4 edges) and SCSC (2 opposite edges simply supported and other 2 edges clamped). A MATLAB program was developed to compute the critical buckling and natural frequencies with different values of dimensional parameters, aspect ratios and length-to-thickness ratios. The research results, in comparison with those from the ABAQUS finite element analysis and previous literatures, are consistent with the latter ones. The examples show that, the size effects significantly influence the buckling load and the natural frequency.
-
Key words:
- couple stress /
- size effect /
- Mindlin plate theory /
- buckling /
- vibration
-
图 2 微元体各面上的应力和偶应力分布状态
Figure 2. The distributions of the stress and the couple stress on the surfaces of a cubic micro element
图 3 各向同性微纳米板微元体的受力平衡状态
Figure 3. The force and moment equilibrium of a micro element of the isotropic micro-nano plate
图 6 SSSS和SCSC边界下微纳米板的临界屈曲荷载随厚长比的变化
Figure 6. Effects of the relative depth on the buckling load of the micro-nano plate under SSSS and SCSC
图 7 不同厚长比下，微纳米板临界屈曲荷载随尺寸参数的变化：（a）SSSS；（b）SCSC
Figure 7. Effects of the dimensional parameters on the buckling load of the micro-nano plate for different thickness-to-length ratios: (a) SSSS; (b) SCSC
图 8 不同尺寸参数下，SSSS微纳米板固有频率随厚长比的变化
Figure 8. Effects of the thickness-to-length ratio on the natural frequency of the SSSS micro-nano plate for different values of dimensional parameters
-
[1] FLECK N A, MULLER G M, ASHBY M F, et al. Strain gradient plasticity: theory and experiment[J]. Acta Metallurgica et Materialia, 1994, 42(2): 475-487. doi: 10.1016/0956-7151(94)90502-9 [2] TOUPIN R A. Elastic materials with couple-stresses[J]. Archive for Rational Mechanics and Analysis, 1962, 11(1): 385-414. doi: 10.1007/BF00253945 [3] MINDLIN R D. Influence of couple-stresses on stress concentrations[J]. Experimental Mechanics, 1963, 3(1): 1-7. doi: 10.1007/BF02327219 [4] FLECK N A, HUTCHINSON J W. A phenomenological theory for strain gradient effects in plasticity[J]. Journal of the Mechanics and Physics of Solids, 1993, 41(12): 1825-1857. doi: 10.1016/0022-5096(93)90072-N [5] YANG F, CHONG A C M, LAM D C C, et al. Couple stress based strain gradient theory for elasticity[J]. International Journal of Solids and Structures, 2002, 39(10): 2731-2743. doi: 10.1016/S0020-7683(02)00152-X [6] SIMSEK M. Nonlinear static and free vibration analysis of microbeams based on the nonlinear elastic foundation using modified couple stress theory and He’s variational method[J]. Composite Structures, 2014, 112(1): 264-272. [7] WANG Y G, LIN W H, LIU N. Nonlinear bending and post-buckling of extensible microscale beams based on modified couple stress theory[J]. Applied Mathematical Modelling, 2015, 39(1): 117-127. doi: 10.1016/j.apm.2014.05.007 [8] WANG Y G, LIN W H, ZHOU C L, et al. Thermal postbuckling and free vibration of extensible microscale beams based on modified couple stress theory[J]. Journal of Mechanics, 2015, 31(1): 37-46. doi: 10.1017/jmech.2014.47 [9] TSIATAS G C. A new Kirchhoff plate model based on a modified couple stress theory[J]. International Journal of Solids and Structures, 2009, 46(13): 2757-2764. doi: 10.1016/j.ijsolstr.2009.03.004 [10] MA H M, GAO X L, REDDY J N. A non-classical Mindlin plate model based on a modified couple stress theory[J]. Acta Mechanica, 2011, 220(1/4): 217-235. [11] ZHOU S S, GAO X L. A nonclassical model for circular Mindlin plates based on a modified couple stress theory[J]. Journal of Applied Mechanics, 2014, 81(5): 1-8. [12] REDDY J N, BERRY J. Nonlinear theories of axisymmetric bending of functionally graded circular plates with modified couple stress[J]. Composite Structures, 2012, 94(12): 3664-3668. doi: 10.1016/j.compstruct.2012.04.019 [13] GAO X, HUANG J, REDDY J. A non-classical third-order shear deformation plate model based on a modified couple stress theory[J]. Acta Mechanica, 2013, 224(11): 2699-2718. doi: 10.1007/s00707-013-0880-8 [14] CHEN W J, LI L, XU M. A modified couple stress model for bending analysis of composite laminated beams with first order shear deformation[J]. Composite Structures, 2011, 93(11): 2723-2732. doi: 10.1016/j.compstruct.2011.05.032 [15] 李莉, 陈万吉, 郑楠. 修正偶应力理论层合薄板稳定性模型及尺度效应[J]. 工程力学, 2013, 30(5): 1-7. (LI Li, CHEN Wanji, ZHENG Nan. Model of composite laminated thin plate based on modified couple stress theory and buckling analysis of scale effect[J]. Engineering Mechanics, 2013, 30(5): 1-7.(in Chinese)LI Li, CHEN Wanji, ZHENG Nan. Model of composite laminated thin plate based on modified couple stress theory and buckling analysis of scale effect[J]. Engineering Mechanics, 2013, 30(5): 1-7. (in Chinese)) [16] 李莉, 陈万吉, 李小鹏. 修正偶应力理论层合薄板自由振动模型及尺度效应[J]. 大连理工大学学报, 2013, 53(3): 313-321. (LI Li, CHEN Wanji, LI Xiaopeng. Free vibration model of composite laminated thin plate based on modified couple stress theory and scale effects[J]. Journal of Dalian University of Technology, 2013, 53(3): 313-321.(in Chinese) doi: 10.7511/dllgxb201303001LI Li, CHEN Wanji, LI Xiaopeng. Free vibration model of composite laminated thin plate based on modified couple stress theory and scale effects[J]. Journal of Dalian University of Technology, 2013, 53(3): 313-321. (in Chinese)) doi: 10.7511/dllgxb201303001 [17] CHEN W J, LI X P. Size-dependent free vibration analysis of composite laminated Timoshenko beam based on new modified couple stress theory[J]. Archive of Applied Mechanics, 2013, 83(3): 431-444. doi: 10.1007/s00419-012-0689-2 [18] 陈万吉, 任鹤飞. 基于新修正偶应力理论的Mindlin层合板自由振动分析[J]. 工程力学, 2016, 33(12): 31-37, 43. (CHEN Wanji, REN Hefei. Free vibration analysis of a laminated composite Mindlin plate based on new modified couple stress theory[J]. Engineering Mechanics, 2016, 33(12): 31-37, 43.(in Chinese) doi: 10.6052/j.issn.1000-4750.2015.05.0394CHEN Wanji, REN Hefei. Free vibration analysis of a laminated composite Mindlin plate based on new modified couple stress theory[J]. Engineering Mechanics, 2016, 33(12): 31-37, 43. (in Chinese)) doi: 10.6052/j.issn.1000-4750.2015.05.0394 [19] 陈万吉, 薛继伟. 新修正偶应力理论Reddy型层合板稳定分析[J]. 计算力学学报, 2017, 34(2): 162-167. (CHEN Wanji, XUE Jiwei. Stability analysis of composite laminated Reddy plate based on new modified couple-stress theory[J]. Chinese Journal of Computational Mechanics, 2017, 34(2): 162-167.(in Chinese) doi: 10.7511/jslx201702006CHEN Wanji, XUE Jiwei. Stability analysis of composite laminated Reddy plate based on new modified couple-stress theory[J]. Chinese Journal of Computational Mechanics, 2017, 34(2): 162-167. (in Chinese)) doi: 10.7511/jslx201702006 [20] 周博, 王志勇, 赵飞, 等. Bernoulli-Euler微梁振动特性的尺寸效应[J]. 中国石油大学学报(自然科学版), 2021, 45(1): 151-157. (ZHOU Bo, WANG Zhiyong, ZHAO Fei, et al. Size effect of vibration characteristics of Bernoulli-Euler microbeam[J]. Journal of China University of Petroleum (Edition of Natural Science) , 2021, 45(1): 151-157.(in Chinese)ZHOU Bo, WANG Zhiyong, ZHAO Fei, et al. Size effect of vibration characteristics of Bernoulli-Euler microbeam[J]. Journal of China University of Petroleum (Edition of Natural Science), 2021, 45(1): 151-157. (in Chinese)) [21] 张大千, 王云鹏, 王玺鉴. 各向异性修正偶应力Mindlin层合板的有限元热稳定性分析[J]. 沈阳航空航天大学学报, 2020, 37(2): 10-20. (ZHANG Daqian, WANG Yunpeng, WANG Xijian. Study on thermal stability of anisotropic modified coupled stressed Mindlin laminates by finite element methods[J]. Journal of Shenyang Aerospace University, 2020, 37(2): 10-20.(in Chinese) doi: 10.3969/j.issn.2095-1248.2020.02.002ZHANG Daqian, WANG Yunpeng, WANG Xijian. Study on thermal stability of anisotropic modified coupled stressed Mindlin laminates by element methods[J]. Journal of Shenyang Aerospace University, 2020, 37(2): 10-20. (in Chinese)) doi: 10.3969/j.issn.2095-1248.2020.02.002 [22] PAGANO N J. Exact solutions for rectangular bidirectional composites and sandwich plates[J]. Journal of Composite Materials, 1970, 4(1): 20-34. doi: 10.1177/002199837000400102 -
下载:
计量
- 文章访问数: 520
- HTML全文浏览量: 311
- PDF下载量: 64
- 被引次数: 0
渝公网安备50010802005915号