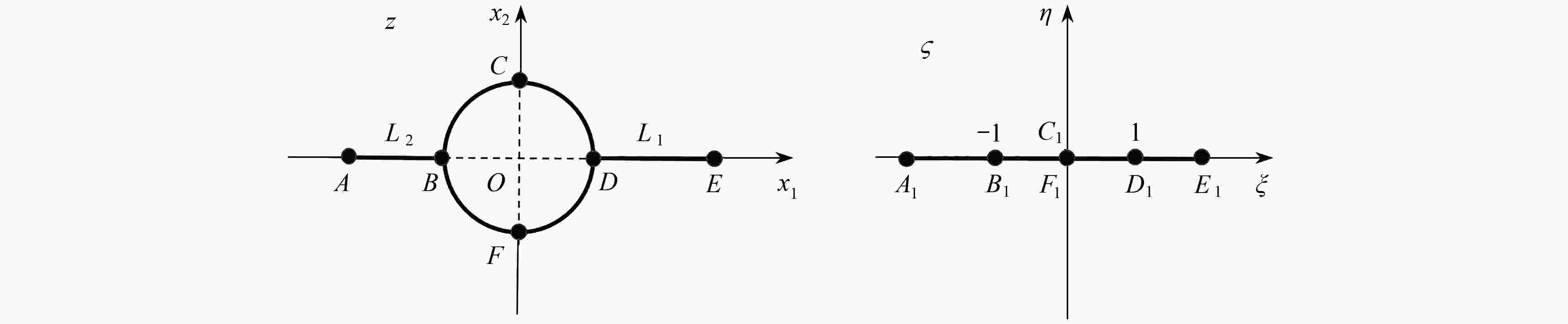The Anti-Plane Problem of Collinear Interface Cracks Emanating From a Circular Hole in 1D Hexagonal Quasicrystal Bi-Materials
-
摘要:
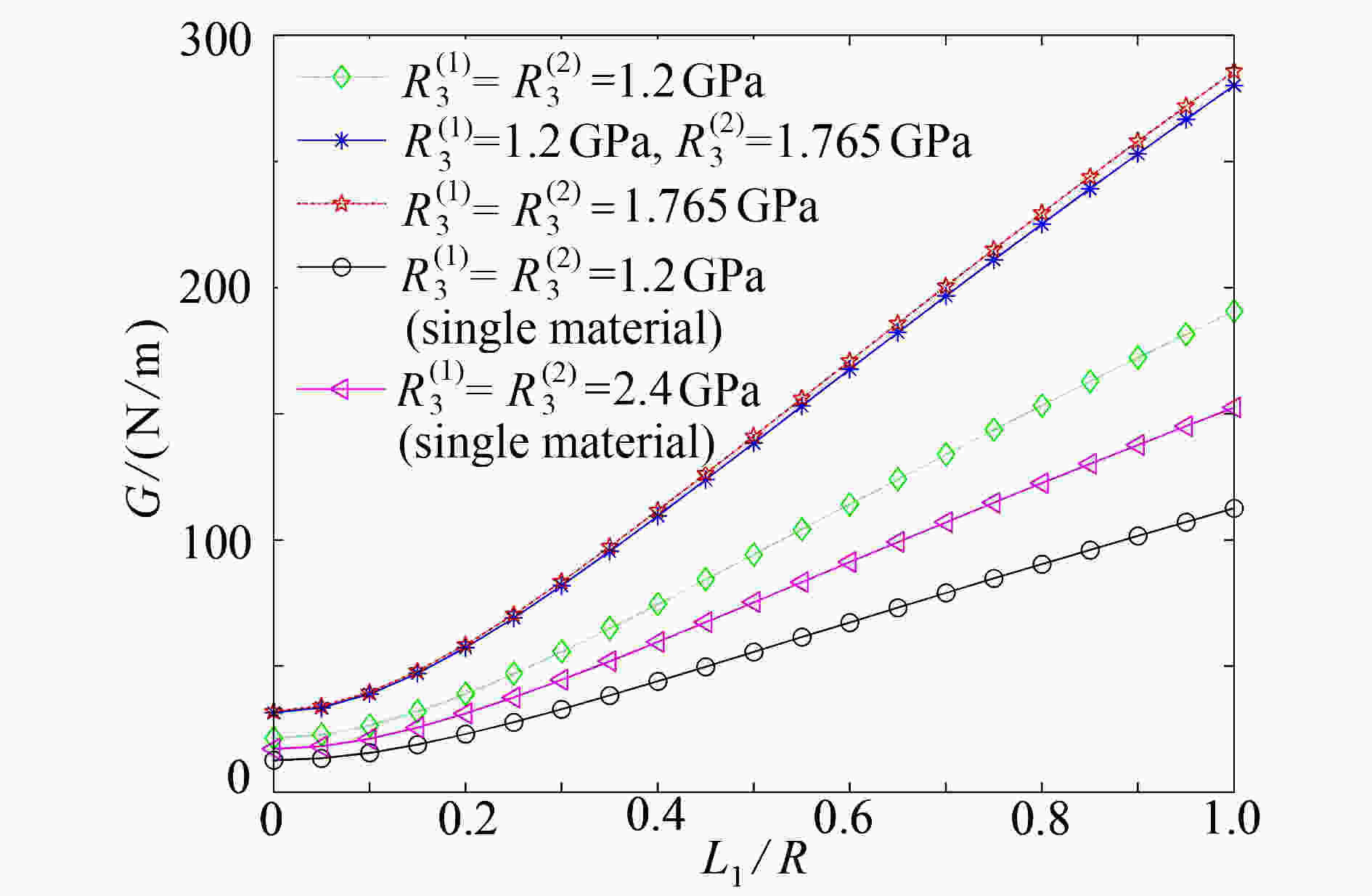
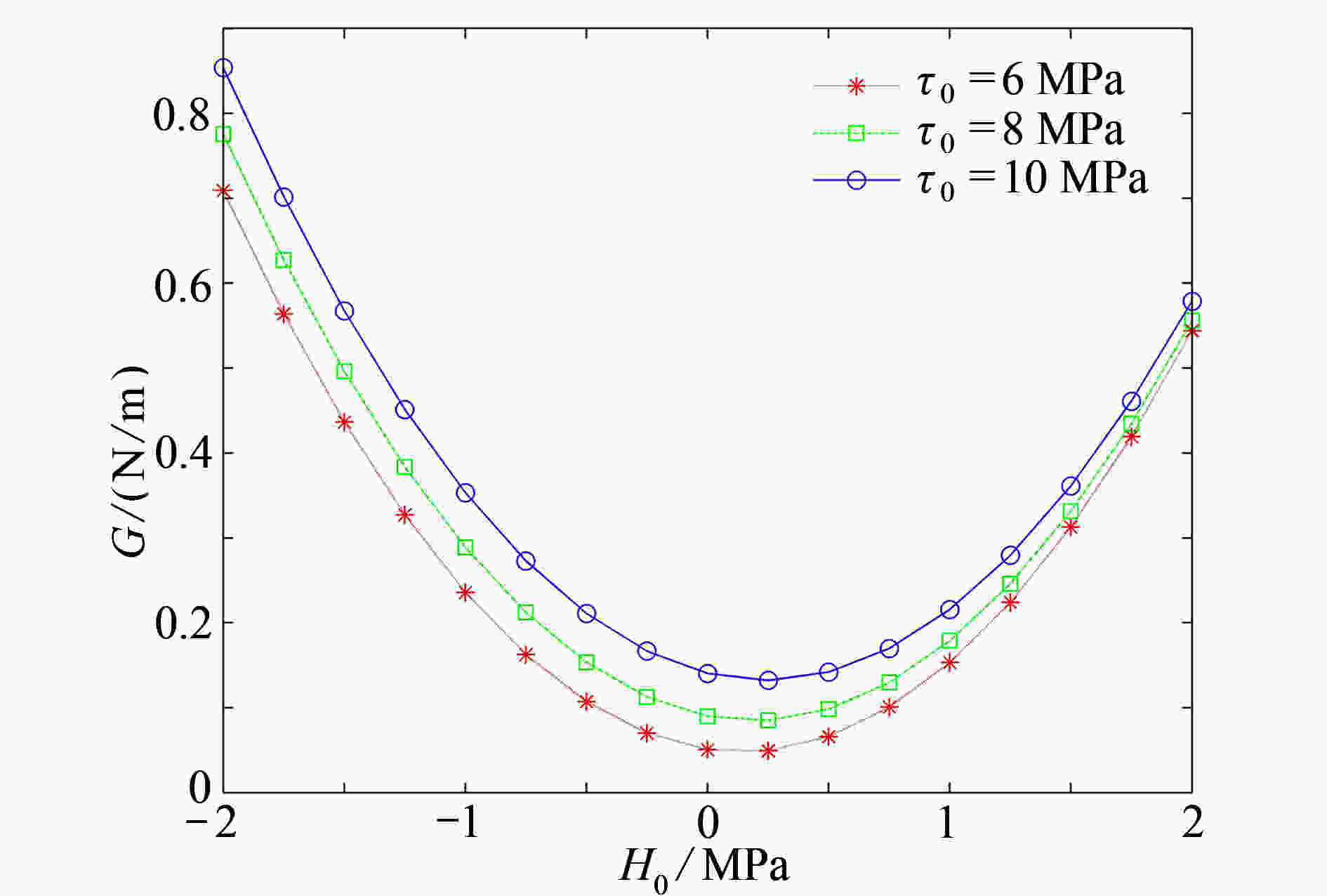
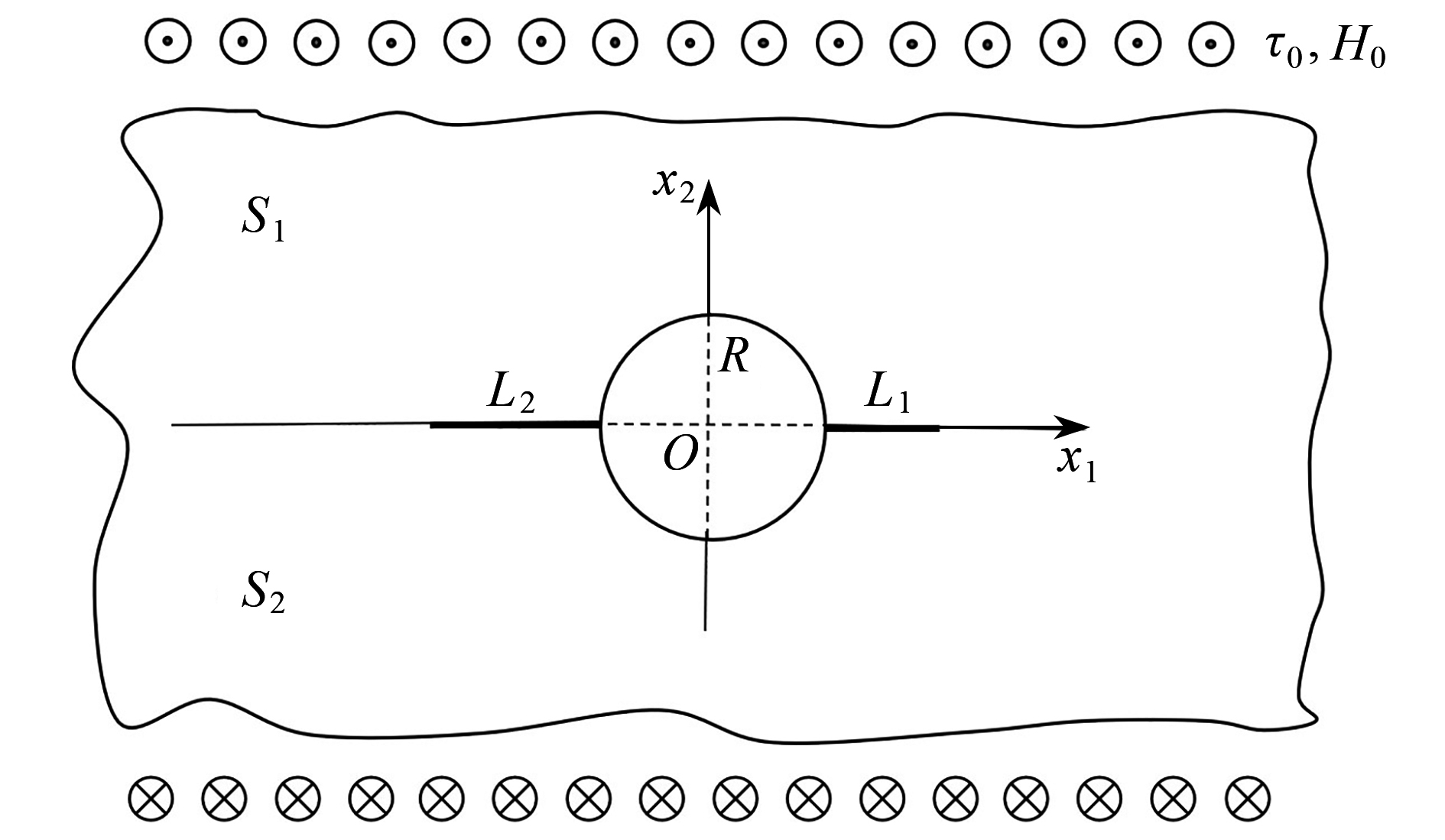
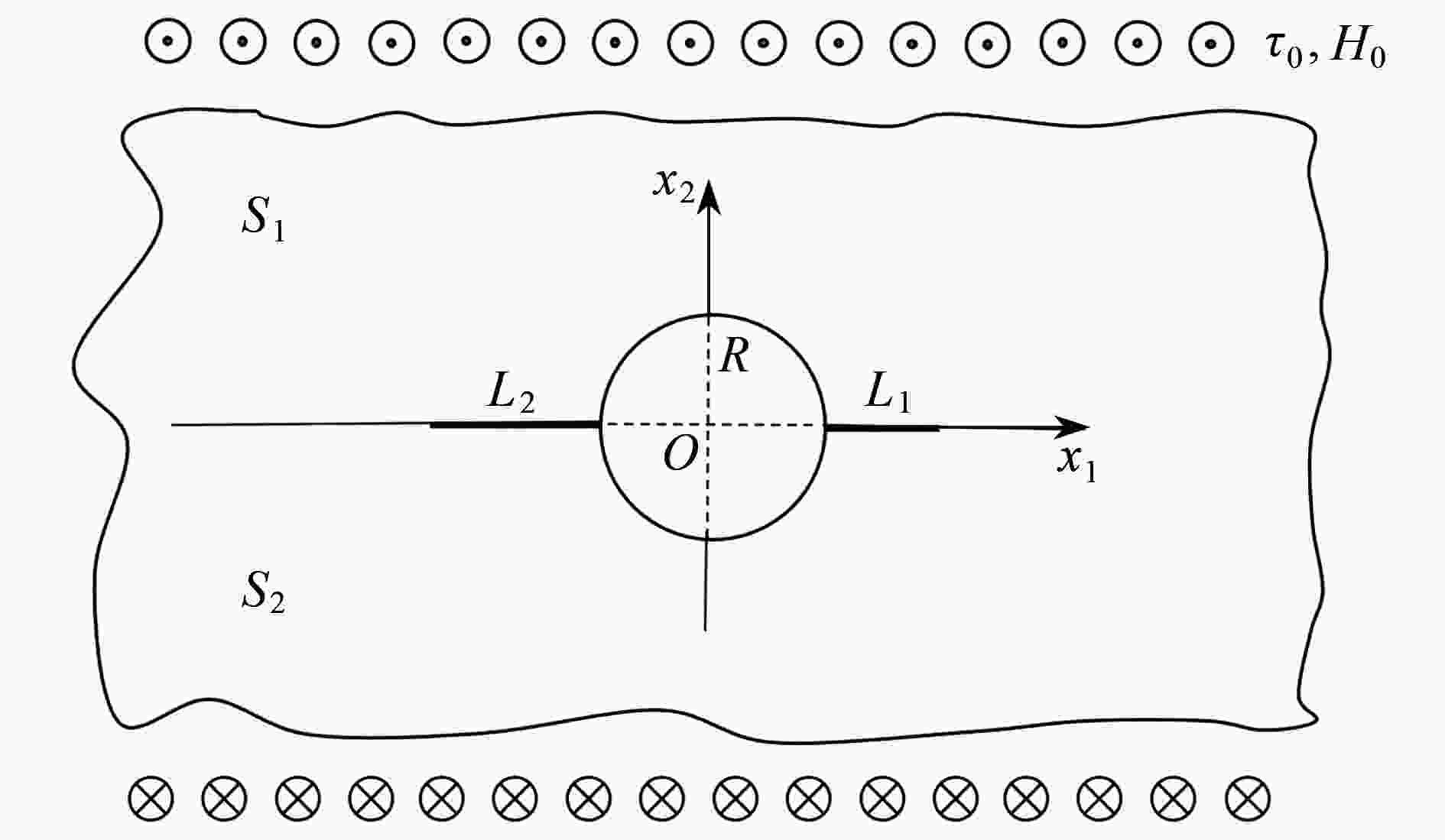
研究了一维六方准晶双材料中圆孔边不对称共线界面裂纹的反平面问题。利用Stroh公式和复变函数方法得到了声子场和相位子场耦合作用下的复势函数，给出了裂纹尖端应力强度因子和能量释放率的解析表达式。通过数值算例，讨论了圆孔半径和裂纹长度对应力强度因子的影响，以及耦合系数、声子场应力和相位子场应力对能量释放率的影响。结果表明：当圆孔半径不变时，应力强度因子随右裂纹长度的增大趋向稳定值。当相位子场应力取一定值时，能量释放率达到最小值，说明特定的相位子场应力可以抑制裂纹的扩展。
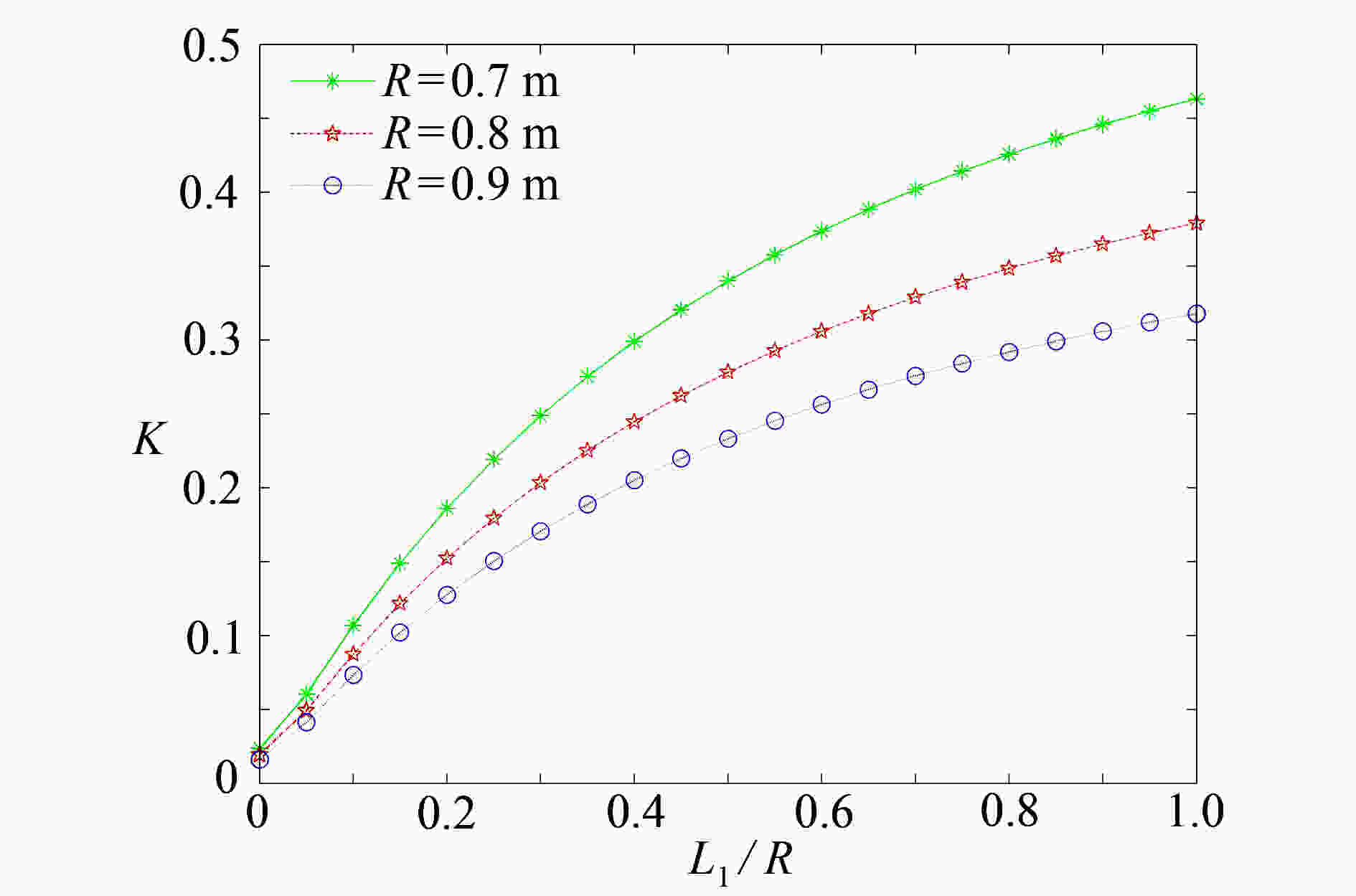
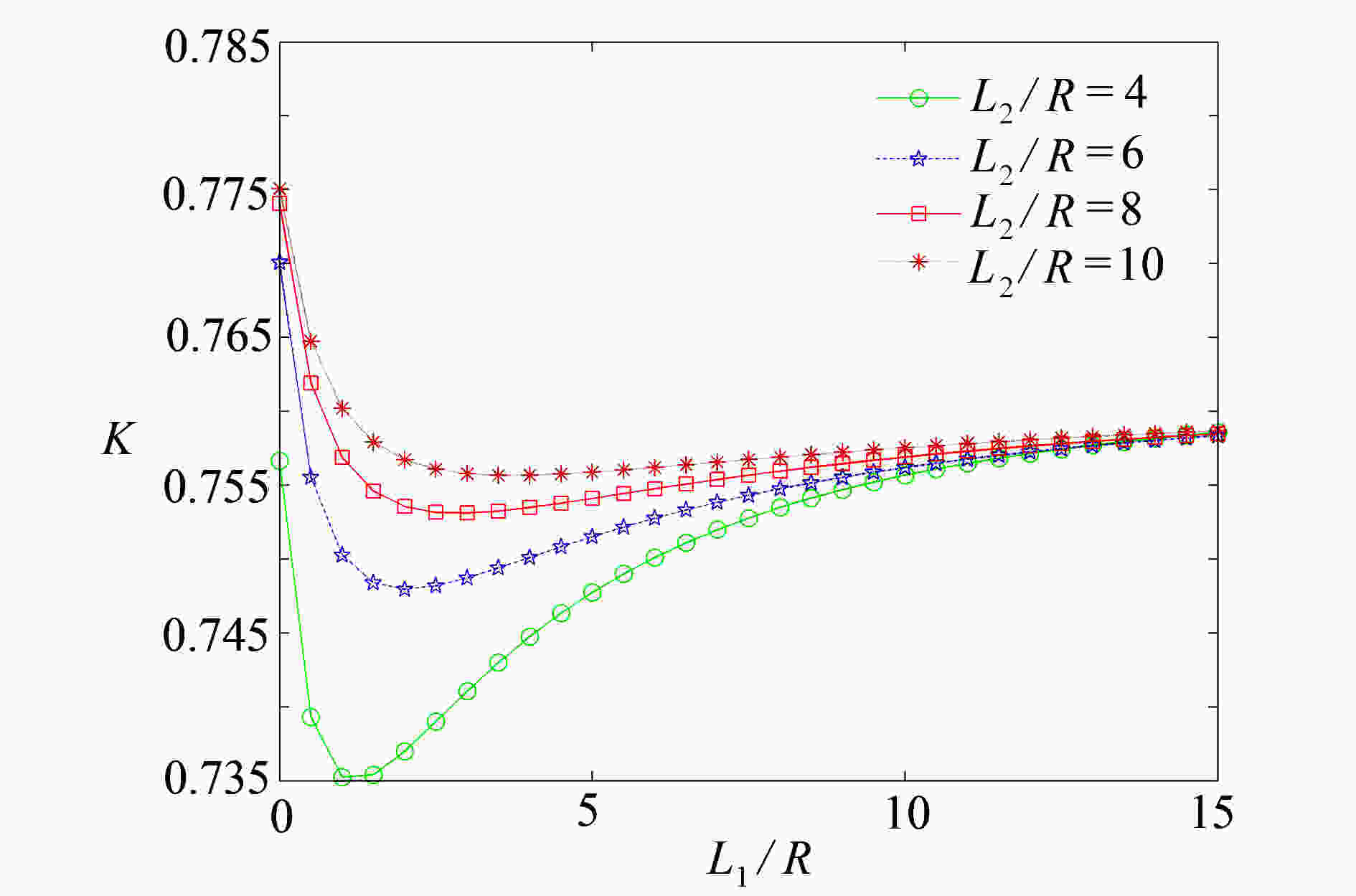
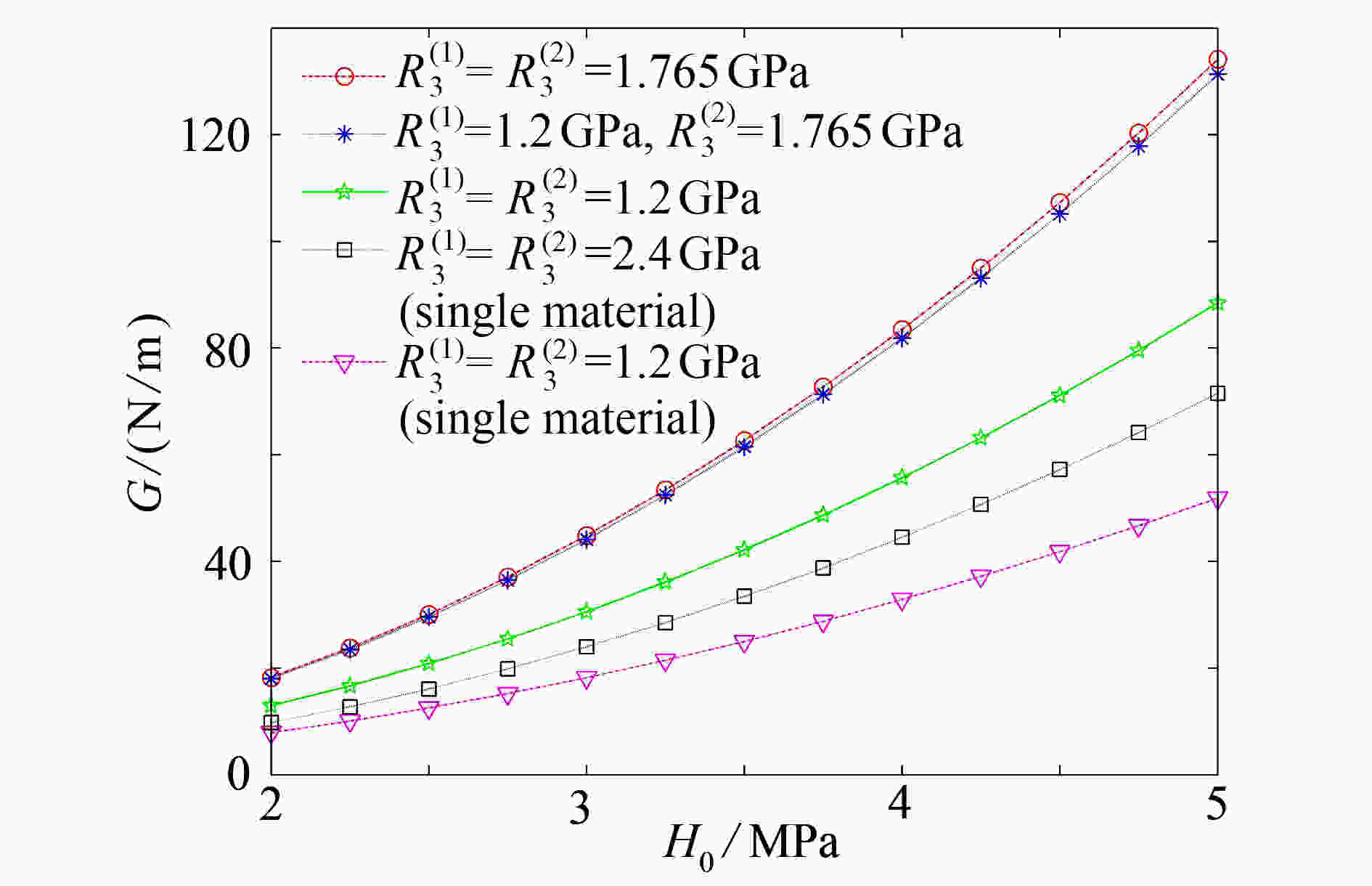
Abstract:The anti-plane problem of asymmetric collinear interface cracks emanating from a circular hole in 1D hexagonal quasicrystal bi-materials was studied. With the Stroh formula and the complex function method, the complex potential functions under the coupling action of the phonon field and the phason field were obtained. The analytical expressions of the stress intensity factor (SIF) and the energy release rate (ERR) at the crack tip were given. The effects of the circular hole radius and the crack length on the SIF, and the effects of the coupling coefficient, the phonon field stress and the phason field stress on the ERR, were discussed. The results show that, the SIF tends to be stable with the increase of the right crack length for a constant circular hole radius. For a certain phason field stress value, the ERR reaches the minimum value, which indicates that a specific phason field stress can inhibit the crack growth.
-
Key words:
- quasicrystal bi-material /
- circular hole /
- interface crack /
- complex function method
-
图 1 含圆孔孔边界面裂纹的一维六方准晶双材料
Figure 1. One dimensional hexagonal quasicrystal bi-materials with interface cracks emanating from a circular hole
图 3 不同的R, K随
$ {{{L_1}} / R} $ 的变化情形Figure 3. For different R values, the change of K with
$ {{{L_1}} /R} $ 
图 4 不同
$ {{{L_2}}/ R} $ , K随$ {{{L_1}} /R} $ 的变化情形Figure 4. For different
$ {{{L_2}} / R} $ values, the change of K with$ {{{L_1}} /R} $ 
图 6 不同的R3, G随
$ {{{L_1}}/ R} $ 的变化情形Figure 6. For different R3 values, the change of G with
$ {{{L_1}}/R} $ 
图 7 不同
$ {\tau _0} $ 作用下, G随$ {H_0} $ 的变化情形Figure 7. For different
$ {\tau _0} $ values, the change of G with$ {H_0} $ -
[1] SHECHTMAN D, BLECH I, GRATIAS D, et al. Metallic phase with long-range orientational order and no translational symmetry[J]. Physical Review Letters, 1984, 53(20): 1951-1954. doi: 10.1103/PhysRevLett.53.1951 [2] 孟祥敏, 佟百运, 吴玉琨. Al65Cu20Co15准晶体的力学性能[J]. 金属学报, 1994, 30(2): 61-64. (MENG Xiangmin, TONG Baiyun, WU Yukun. Mechanical properties of Al65Cu20Co15 quasicrystal[J]. Acta Metallurgica Sinica, 1994, 30(2): 61-64.(in Chinese)MENG Xiangmin, TONG Baiyun, WU Yukun. Mechanical properties of Al65Cu20Co15 quasicrystal[J]. Acta Metallurgica Sinica, 1994, 30(2): 61-64. (in Chinese)) [3] FAN T Y, LI X F, SUN Y F. A moving screw dislocation in a one-dimensional hexagonal quasicrystal[J]. Acta Physica Sinica (Overseas Edition) , 1999, 8(4): 288-295. doi: 10.1088/1004-423X/8/4/007 [4] LI L F, FAN T Y. Exact solutions of two semi-infinite collinear cracks in a strip of one dimensional hexagonal quasicrystal[J]. Applied Mathematics and Computation, 2008, 196(1): 1-5. doi: 10.1016/j.amc.2007.05.028 [5] WANG X, PAN E. Analytical solutions for some defect problems in 1D hexagonal and 2D octagonal quasicrystals[J]. Pramana, 2008, 70(5): 911-933. doi: 10.1007/s12043-008-0099-8 [6] ZHOU J M, LI L H, Wang G X. Dynamic problems in a decagonal quasicrystal with a mode Ⅱ Griffith crack[J]. Chinese Journal of Engineering Mathematics, 2021, 38(1): 136-150. [7] 郭俊宏, 刘官厅. 一维六方准晶中具有不对称裂纹的圆形孔口问题的解析解[J]. 应用数学学报, 2007, 30(6): 1066-1075. (GUO Junhong, LIU Guanting. Analytic solutions of the one-dimensional hexagonal quasicrystals about problem of a circular hole with asymmetry cracks[J]. Acta Mathematicae Applicatae Sinica, 2007, 30(6): 1066-1075.(in Chinese) doi: 10.3321/j.issn:0254-3079.2007.06.012GUO Junhong, LIU Guanting. Analytic solutions of the one-dimensional hexagonal quasicrystals about problem of a circular hole with asymmetry cracks[J]. Acta Mathematicae Applicatae Sinica, 2007, 30(6): 1066-1075. (in Chinese)) doi: 10.3321/j.issn:0254-3079.2007.06.012 [8] 郭俊宏, 刘官厅. 一维六方准晶中带双裂纹的椭圆孔口问题的解析解[J]. 应用数学和力学, 2008, 29(4): 439-446. (GUO Junhong, LIUGuanting. Analytic solutions of problem about an elliptic hole with two straight cracks in one-dimensional hexagonal quasicrystals[J]. Applied Mathematics and Mechanics, 2008, 29(4): 439-446.(in Chinese) doi: 10.3879/j.issn.1000-0887.2008.04.006GUO Junhong, LIUGuanting. Analytic solutions of problem about an elliptic hole with two straight cracks in one-dimensional hexagonal quasicrystals[J]. Applied Mathematics and Mechanics, 2008, 29(4): 439-446. (in Chinese)) doi: 10.3879/j.issn.1000-0887.2008.04.006 [9] GUO J H, LIU G T. Exact analytic solutions for an elliptic hole with asymmetric collinear cracks in a one-dimensional hexagonal quasi-crystal[J]. Chinese Physics B, 2008, 17(7): 2610-2620. doi: 10.1088/1674-1056/17/7/044 [10] GUO J H, LU Z X. Exact solution of four cracks originating from an elliptical hole in one-dimensional hexagonal quasicrystals[J]. Applied Mathematics and Computation, 2011, 217(22): 9397-9403. doi: 10.1016/j.amc.2011.04.028 [11] LI L H, LIU G T. Interaction of a dislocation with an elliptical hole in icosahedral quasicrystals[J]. Philosophical Magazine Letters, 2013, 93(3): 142-151. doi: 10.1080/09500839.2012.752883 [12] YANG J, LI X, DING S H. Anti-plane analysis of a circular hole with three unequal cracks in one-dimensional hexagonal piezoelectric quasicrystals[J]. Chinese Journal of Engineering Mathematics, 2016, 33(2): 184-198. [13] 白巧梅, 丁生虎. 一维六方压电准晶中正六边形孔边裂纹的反平面问题[J]. 应用数学和力学, 2019, 40(10): 1071-1080. (BAI Qiaomei, DING Shenghu. An anti-plane problem of cracks at edges of regular hexagonal holes in 1D hexagonal piezoelectric quasicrystals[J]. Applied Mathematics and Mechanics, 2019, 40(10): 1071-1080.(in Chinese)BAI Qiaomei, DING Shenghu. An anti-plane problem of cracks at edges of regular hexagonal holes in 1D Hexagonal piezoelectric quasicrystals[J]. Applied Mathematics and Mechanics, 2019, 40(10): 1071-1080. (in Chinese)) [14] TUPHOLME G E. An antiplane shear crack moving in one-dimensional hexagonal quasicrystals[J]. International Journal of Solids and Structures, 2015, 71: 255-261. doi: 10.1016/j.ijsolstr.2015.06.027 [15] TUPHOLME G E. Row of shear cracks moving in one-dimensional hexagonal quasicrystal line materials[J]. Engineering Fracture Mechanics, 2015, 134: 451-458. doi: 10.1016/j.engfracmech.2014.07.002 [16] EL-BORGI S, ERDOGAN F, HATIRA F B. An interface crack between a functionally graded coating and a homogeneous substrate under thermo-mechanical loading[J]. Materials Science Forum, 2003, 423/425: 601-606. doi: 10.4028/www.scientific.net/MSF.423-425.601 [17] KUANG J S, WANG Y H. Analysis of interfacial cracks emanating from a hole in a bi-material plate[J]. European Journal of Mechanics A: Solids, 1999, 18(3): 465-479. doi: 10.1016/S0997-7538(99)00116-3 [18] LOBODA V, KOMAROV O, BILYI D, et al. An analytical approach to the analysis of an electrically permeable interface crack in a 1D piezoelectric quasicrystal[J]. Acta Mechanica, 2020, 231(8): 3419-3433. doi: 10.1007/s00707-020-02721-8 [19] SONG T S, HASSAN A. Dynamic anti-plane analysis for symmetrically radial cracks near a non-circular cavity in piezoelectric bi-materials[J]. Acta Mechanica, 2015, 226(7): 2089-2101. doi: 10.1007/s00707-015-1303-9 [20] AN N, SONG T S, HOU G L. Interfacial cracks near an eccentric circular hole in piezoelectric bi-materials subjected to dynamic incident anti-plane shearing[J]. AIP Advances, 2020, 10(5): 1-11. [21] AN N, SONG T S. Dynamic fracture behavior for functionally graded piezoelectric bi-materials with interfacial cracks near a circular hole[J]. Waves in Random and Complex Media, 2021: 1-19. DOI: 10.1080/17455030.2021.1936284. [22] ZHANG L L, WU D, XU W S, et al. Green’s functions of one-dimensional quasicrystal bi-material with piezoelectric effect[J]. Physics Letters A, 2016, 380(39): 3222-3228. doi: 10.1016/j.physleta.2016.07.043 [23] HU K Q, GAO C F, ZHENG Z, et al. Interaction of collinear interface cracks between dissimilar one-dimensional hexagonal piezoelectric quasicrystals[J]. ZAMM: Zeitschrift fur Angewandte Mathematic und Mechanik, 2021, 101(11): 1-26. doi: 10.1002/zamm.202000360 [24] HU K Q, JIN H, YANG Z J, et al. Interface crack between dissimilar one-dimensional hexagonal quasicrystals with piezoelectric effect[J]. Acta Mechanica, 2019, 230(7): 2455-2474. doi: 10.1007/s00707-019-02404-z [25] FAN C Y, CHEN S, ZHANG Q Y, et al. Fundamental solutions and analysis of an interfacial crack in a one-dimensional hexagonal quasicrystal bi-material[J]. Mathematics and Mechanics of Solids, 2020, 25(5): 1124-1139. doi: 10.1177/1081286520903085 [26] ZHAO M H, FAN C Y, LU C S, et al. Analysis of interface cracks in one-dimensional hexagonal quasi-crystal coating under in-plane loads[J]. Engineering Fracture Mechanics, 2021, 243: 107534. doi: 10.1016/j.engfracmech.2021.107534 [27] FAN T Y. Mathematical Theory of Elasticity of Quasicrystals and Its Application[M]. Beijing: Science Press, 2010. [28] MUSKHELISHVILI N I. Some Basic Problems of the Mathematical Theory of Elasticity[M]. Groningen, Holland: Noordhoff, 1953. [29] 杨娟. 压电效应下一维六方准晶中孔边多裂纹反平面断裂问题研究[D]. 博士学位论文. 银川: 宁夏大学, 2015.YANG Juan. Study on anti-plane fracture problems of Multiple cracks emanating from a hole in one-dimensional hexagonal quasicrystals with piezoelectric effects[D]. PhD Thesis. Yinchuan: Ningxia University, 2015. (in Chinese) [30] ZHOU Y B, LI X F. Exact solution of two collinear cracks normal to the boundaries of a 1D layered hexagonal piezoelectric quasicrystal[J]. Philosophical Magazine, 2018, 98(19): 1780-1798. doi: 10.1080/14786435.2018.1459057 -
下载:
点击查看大图
计量
- 文章访问数: 237
- HTML全文浏览量: 142
- PDF下载量: 27
- 被引次数: 0
