Structural Instantaneous Frequency Identification Based on the Fractional Fourier Transform
-
摘要:
为识别时变信号的瞬时频率，由分数阶Fourier变换定义推导出了一般信号的频率与单一变量旋转角度α的关系式，从理论上解释了分数阶Fourier变换本质上是一种普通Fourier变换结合伸缩平移窗的算法，进而在分数阶Fourier域建立了非平稳信号瞬时频率的一般表达式，实现了结构瞬时频率的识别。采用任意非线性调频信号仿真算例和三自由度有阻尼时变结构系统的数值算例对提出的方法进行了比较分析。结果表明，该文提出的方法与理论值吻合良好，并具有一定的抗噪性，验证了方法的可靠性和实用性，可以应用于时变结构瞬时频率的识别。
-
关键词:
- 分数阶Fourier变换 /
- 非平稳信号 /
- 瞬时频率 /
- 伸缩平移窗 /
- 时变结构
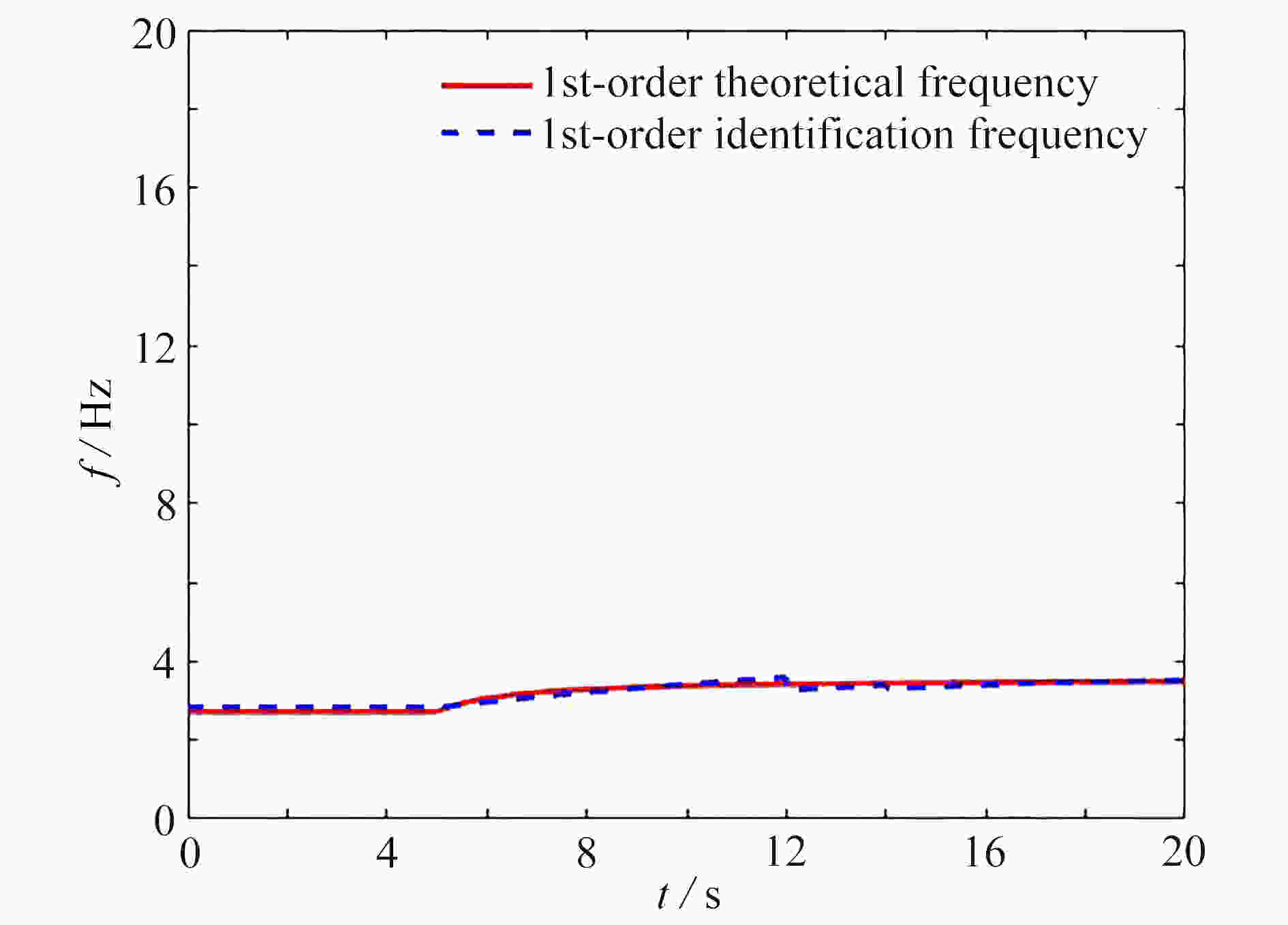
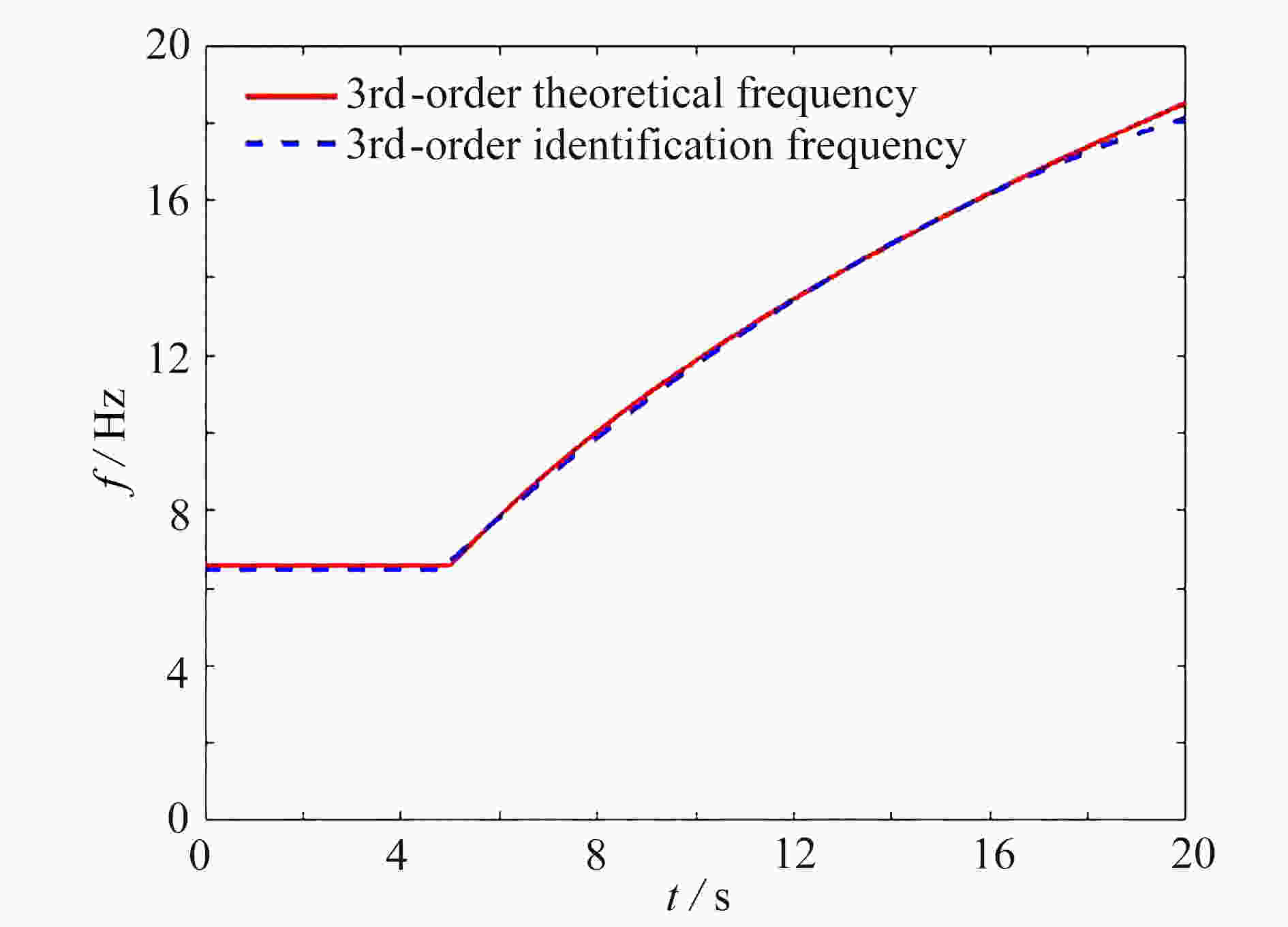
Abstract:To identify the instantaneous frequencies of time-varying signals, the theoretical relationship between the frequency and rotational angle α in a signal was derived based on the definition of the fractional Fourier transform. Then the fractional Fourier transform was interpreted to be essentially an algorithm combining the ordinary Fourier transform with the dilation and translation window. A general expression of the signal instantaneous frequency in the fractional Fourier domain was thereafter formulated so that the structural instantaneous frequency can be extracted accordingly. The feasibility and reliability of the proposed method were verified with a simulated nonlinear frequency modulation signal and a numerical example of a 3DOF damped time-varying structure system. The results show that, the results of the proposed method are in good agreement with the theoretical values, and the method has a certain degree of anti-noise capability. Subsequently, the proposed method is applicable to the identification of the instantaneous frequencies of time-varying structures.
-
图 2 FRFT识别一般信号的原理示意图
Figure 2. Schematic diagram of general signal identification based on the FRFT
图 3 任意非平稳信号关于频率的三维曲面图
Figure 3. The 3D surface of any non-stationary signal with respect to the frequency
图 4 任意非平稳信号时频曲线
Figure 4. The time-frequency distribution of arbitrary nonstationary signals
图 5 加噪信号时域波形：（a） SNR为−10 dB；（b） SNR为10 dB；（c） SNR为20 dB
Figure 5. Time domain waveforms of noised signals: (a) SNR is −10 dB; (b) SNR is 10 dB; (c) SNR is 20 dB
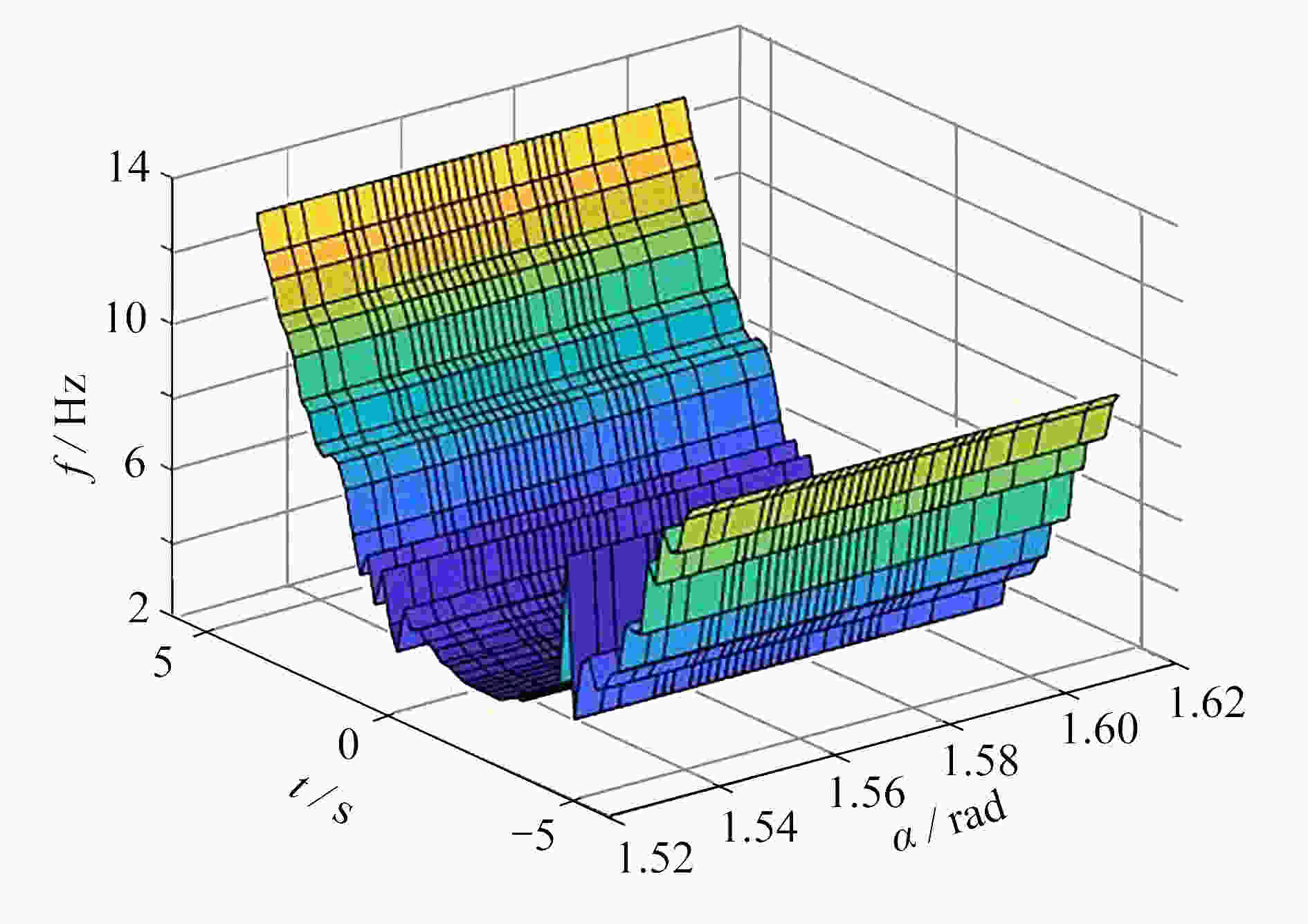
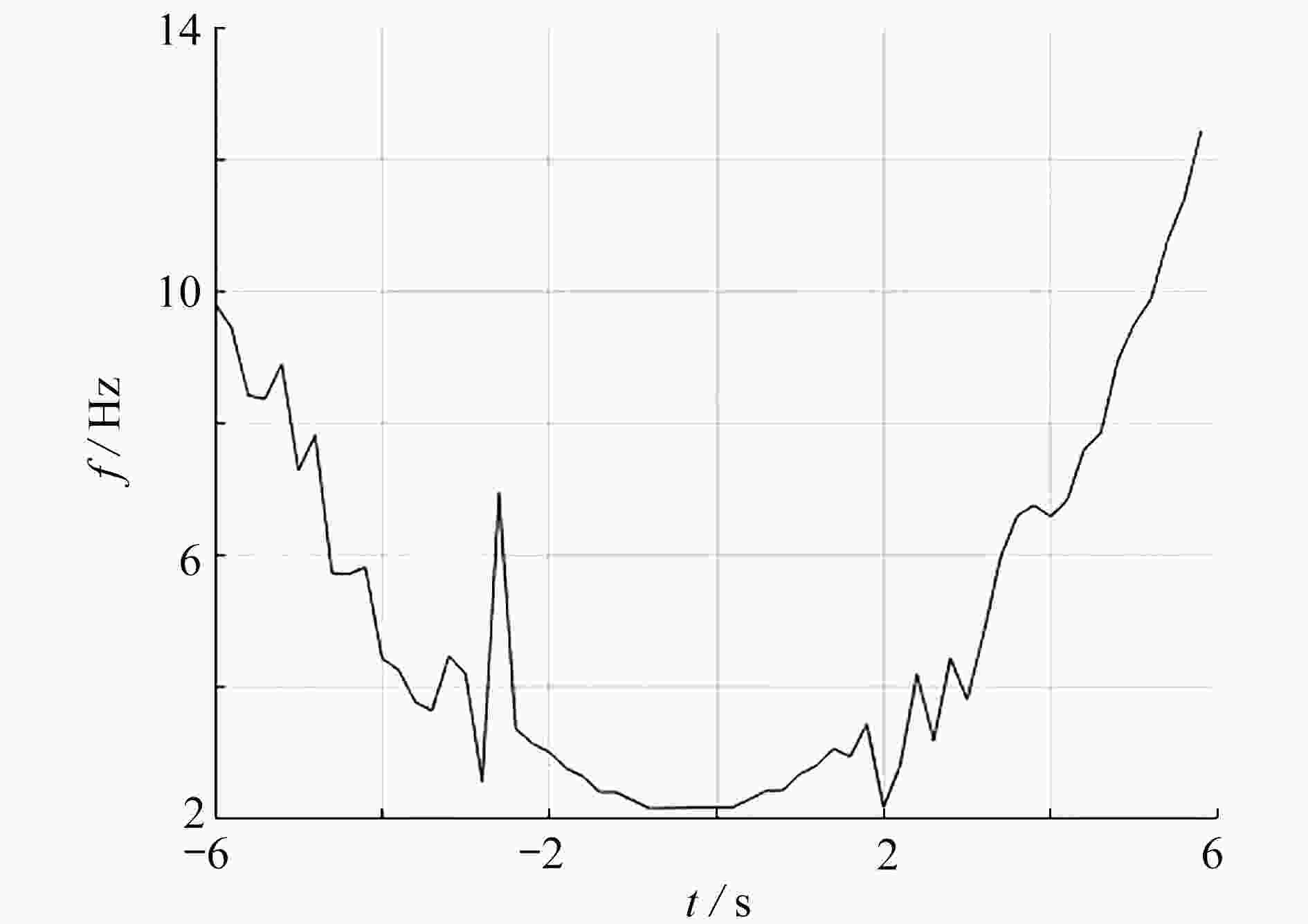
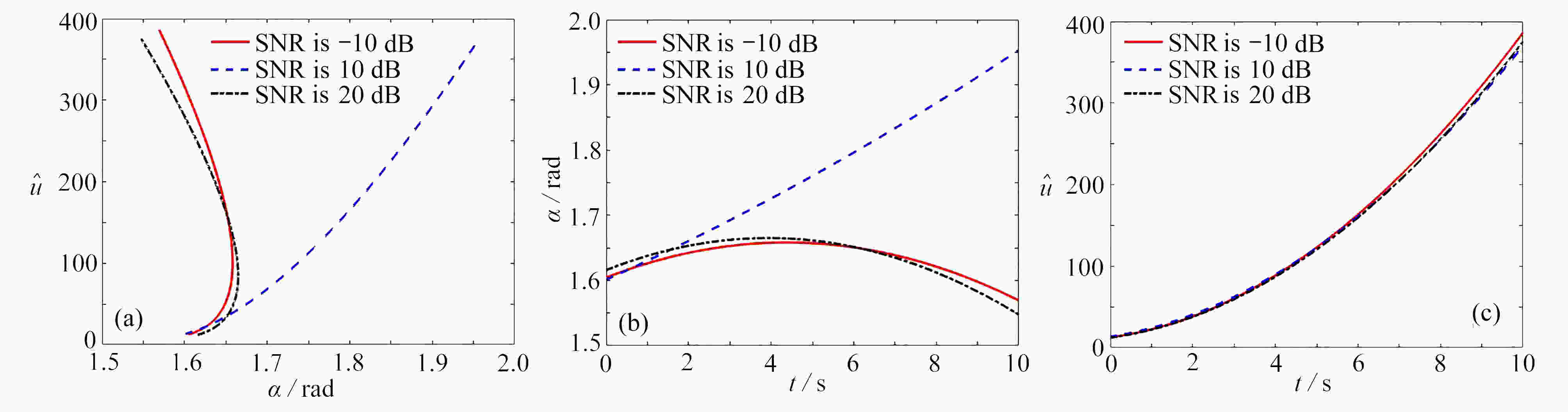
图 6 FRFT对信号瞬时频率的识别过程：（a） α与最佳
$\hat{u} $ 关系曲线；（b） 时间与α关系曲线；（c） 时间与最佳$\hat{u} $ 关系曲线Figure 6. The FRFT identification process of signal instantaneous frequencies: (a) the relationship curve between α and
$\hat{u} $ ; (b) the relationship curve between t and α; (c) the relationship curve between t and$\hat{u} $ 
图 7 FRFT与STFT对信号瞬时频率的识别与理论值的对比：（a） SNR为−10 dB； （b） SNR为10 dB； （c） SNR为20 dB
注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同。
Figure 7. The comparison between FRFT and STFT identification values of signal instantaneous frequencies and theoretical values: (a) SNR is −10 dB; (b) SNR is 10 dB; (c) SNR is 20 dB
图 9 刚度线性变化时结构固有频率
Figure 9. Natural frequencies of the structure with linearly changing stiffness
图 11 FRFT识别及理论结构第一阶固有频率
Figure 11. The FRFT-based identification and the 1st-order theoretical natural frequencies of the structure
图 12 FRFT识别及理论结构第二阶固有频率
Figure 12. The FRFT-based identification and the 2nd-order theoretical natural frequencies of the structure
-
[1] 赵雷, 刘宁国. 大跨度叠合梁斜拉桥多维多点非平稳随机地震响应分析[J]. 应用数学和力学, 2017, 38(1): 118-125ZHAO Lei, LIU Ningguo. Non-stationary random seismic analysis of large-span composite beam cable-stayed bridges under multi-support and multi-dimentional earthquake excitations[J]. Applied Mathematics and Mechanics, 2017, 38(1): 118-125.(in Chinese) [2] HUANG N, SHEN S S P. Hilbert-Huang Transform and Its Applications[M]. Singapore: World Scientific, 2005. [3] FELDMAN M. Theoretical analysis and comparison of the Hilbert transform decomposition methods[J]. Mechanical Systems & Signal Processing, 2008, 22(3): 509-519. [4] BAI R F, LI B Z, CHENG Q Y. Wigner-Ville distribution associated with the linear canonical transform[J]. Journal of Applied Mathematics, 2012, 2012: 740161. [5] MATEO C, TALAVERA J A. Short-time Fourier transform with the window size fixed in the frequency domain[J]. Digital Signal Processing, 2018, 77: 13-21. doi: 10.1016/j.dsp.2017.11.003 [6] SONG J, FAN H Y, YUAN H C. Wavelet transform of quantum chemical states[J]. International Journal of Quantum Chemistry, 2012, 112(11): 2343-2347. [7] 陶然, 齐林, 王越. 分数阶Fourier变换的原理与应用[M]. 北京: 清华大学出版社, 2004.TAO Ran, QI Lin, WANG Yue. Principle and Application of Fractional Fourier Transform[M]. Beijing: Tsinghua University Press, 2004.(in Chinese) [8] FELDMAN M. Time-varying vibration decomposition and analysis based on the Hilbert transform[J]. Journal of Sound and Vibration, 2006, 295(3/5): 518-530. [9] 续秀忠, 张志谊, 华宏星, 等. 结构时变模态参数辨识的时频分析方法[J]. 上海交通大学学报, 2003, 37(1): 122-126 doi: 10.3321/j.issn:1006-2467.2003.01.033XU Xiuzhong, ZHANG Zhiyi, HUA Hongxing, et al. Time-varying modal parameter identification with time-frequency analysis methods[J]. Journal of Shanghai Jiaotong University, 2003, 37(1): 122-126.(in Chinese) doi: 10.3321/j.issn:1006-2467.2003.01.033 [10] PACHORI R B, SIRCAR P. A new technique to reduce cross terms in the Wigner distribution[J]. Digital Signal Processing, 2007, 17(2): 466-474. doi: 10.1016/j.dsp.2006.10.004 [11] CHEN G D, WANG Z C. A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components[J]. Mechanical Systems and Signal Processing, 2012, 28: 258-279. doi: 10.1016/j.ymssp.2011.02.002 [12] 廖庆良. 基于短时傅立叶变换的结构振动模态的识别[D]. 硕士学位论文. 武汉: 华中科技大学, 2004.LIAO Qingliang. Identification of structural vibration mode based on short time Fourier transform[D]. Master Thesis. Wuhan: Huazhong University of Science and Technology, 2004.(in Chinese) [13] CHEN S L, LIU J J, LAI H C. Wavelet analysis for identification of damping ratios and natural frequencies[J]. Journal of Sound and Vibration, 2009, 323(1/2): 130-147. [14] KIJEWSKI T, KAREEM A. Wavelet transforms for system identification in civil engineering[J]. Computer-Aided Civil and Infrastructure Engineering, 2010, 18(5): 339-355. [15] WANG C, REN W X, WANG Z C, et al. Instantaneous frequency identification of time-varying structures by continuous wavelet transform[J]. Engineering Structures, 2013, 52: 17-25. doi: 10.1016/j.engstruct.2013.02.006 [16] 王超, 任伟新, 黄天立. 基于复小波变换的结构瞬时频率识别[J]. 振动工程学报, 2009, 22(5): 492-496 doi: 10.3969/j.issn.1004-4523.2009.05.009WANG Chao, REN Weixin, HUANG Tianli. Structure instantaneous frequency identification based on complex wavelet transform[J]. Journal of Vibration Engineering, 2009, 22(5): 492-496.(in Chinese) doi: 10.3969/j.issn.1004-4523.2009.05.009 [17] 刘景良, 任伟新, 王超, 等. 基于最大坡度法提取非平稳信号小波脊线和瞬时频率[J]. 工程力学, 2018, 35(2): 30-37, 46LIU Jingliang, REN Weixin, WANG Chao, et al. Wavelet ridgeline and instantaneous frequency extraction of nonstationary signal based on maximum slope method[J]. Engineering Mechanics, 2018, 35(2): 30-37, 46.(in Chinese) [18] 陶然, 邓兵, 王越. 分数阶Fourier变换在信号处理领域的研究进展[J]. 中国科学(E辑): 信息科学, 2006, 36(2): 113-136TAO Ran, DENG Bing, WANG Yue. Research progress of fractional Fourier transform in signal processing[J]. Science in China (Series E) : Information Sciences, 2006, 36(2): 113-136.(in Chinese) [19] TAO R, MIAO H X, MA J M. Theory and methods for sampling in fractional domains[C]//2016 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC). Hong Kong, 2016. [20] MENG X Y, TAO R, WANG Y. Fractional Fourier domain analysis of decimation and interpolation[J]. Science in China (Series F) : Information Sciences, 2007, 50(4): 521-538. doi: 10.1007/s11432-007-0040-7 [21] SU X H, TAO R, KANG X J. Analysis and comparison of discrete fractional Fourier transforms[J]. Signal Processing, 2019, 160: 284-298. doi: 10.1016/j.sigpro.2019.01.019 [22] 赵兴浩, 邓兵, 陶然. 分数阶傅里叶变换数值计算中的量纲归一化[J]. 北京理工大学学报, 2005, 25(4): 360-364 doi: 10.3969/j.issn.1001-0645.2005.04.019ZHAO Xinghao, DENG Bing, TAO Ran. Dimension normalization in numerical calculation of fractional Fourier transform[J]. Journal of Beijing Institute of Technology, 2005, 25(4): 360-364.(in Chinese) doi: 10.3969/j.issn.1001-0645.2005.04.019 -
下载:
计量
- 文章访问数: 845
- HTML全文浏览量: 421
- PDF下载量: 112
- 被引次数: 0
渝公网安备50010802005915号