Dynamic Mechanism and Energy Evolution of the Waterwheel Chaotic Rotation
-
摘要: 为了揭示水轮混沌旋转的生成机制,采用力矩分析方法研究了水轮混沌旋转的力学机理与能量转换问题. 把Malkus水轮的数学模型转换为Kolmogorov系统,基于惯性力矩、内力矩、耗散力矩和外力矩的不同耦合模式,利用理论分析和数值仿真相结合的方法,分析探讨了Malkus水轮混沌旋转的主要影响因素和内在的力学机理. 研究了水轮系统Hamilton能量、动能和势能之间的相互转换,讨论了能量与Rayleigh数之间的关系. 影响水轮系统混沌生成的主要因素是外力矩和耗散力矩. 通过分析和仿真得知:力矩缺失模式并不能使系统生成混沌,全力矩模式才能使系统产生混沌,即混沌发生时4种力矩缺一不可,与此同时,只有耗散和外力相匹配时系统才能产生混沌,此时水轮发生混沌旋转. 引进Casimir函数分析了水轮系统的动力学行为和能量转换,并估计了混沌吸引子的界. Casimir函数反映了能量转换和轨道与平衡点间的距离,数值结果仿真刻画了它们之间的关系.
-
关键词:
- Kolmogorov系统 /
- 混沌 /
- 混沌水轮 /
- 力学机理
Abstract: To reveal the mechanism of the waterwheel chaotic rotation, the dynamic mechanism and the energy conversion of the waterwheel chaotic rotation were studied with the method of moment analysis. The mathematical model for the Malkus waterwheel rotation was transformed into the Kolmogorov system. Based on the different coupling modes of inertia moments, internal moments, dissipation moments and external moments, the main factors and internal dynamic mechanisms of the Malkus waterwheel chaotic rotation were analyzed and discussed with the method of theoretical analysis and numerical simulation. The conversion among the Hamiltonian energy, the kinetic energy and the potential energy was investigated. The relationship between the energies and the Rayleigh number was discussed. The main factors influencing the chaotic rotation are the external moments and the dissipation moments. The analysis and simulation results show that, the lack-of-moment mode cannot lead to the system chaos, but the full-moment mode can, i.e., the waterwheel chaotic rotation will occur only in the existence of all 4 types of moments and when the dissipation and external forces match well. The Casimir function was introduced to analyze the system dynamics and the energy conversion. The bounds for the chaotic attractor were obtained with the Casimir function. The Casimir function reflects the energy conversion and the distances between the orbits and the equilibria. Numerical simulations depict the relationships among them.-
Key words:
- Kolmogorov system /
- chaos /
- waterwheel system /
- dynamic mechanism
-
表 1 σ=5, r取不同值时,水轮系统(1)的动力学行为与能量演化及其相应的旋转状态
Table 1. Dynamics behaviors and energy evolutions of system (1) with corresponding actual rotations of the waterwheel for σ=5 and different r values
r-value 0<r<1
r=0, r1=1r>1
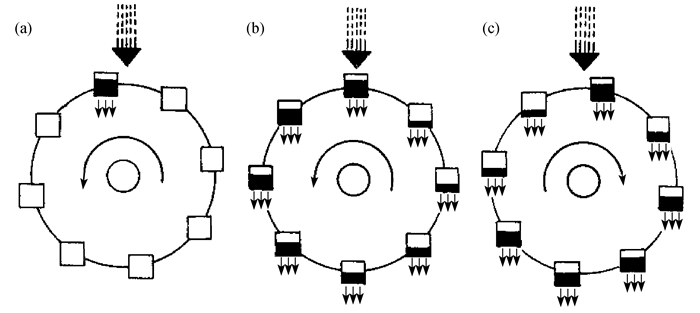
re=1.058 45, rg=13.965 6, rh=15.041 2equilibrium O stable node saddle node (one direction is unstable, the other two directions are stable) equilibrium P± inexistence stable node stable focus stable focus saddle point trajectory of system (4) tendency to stable equilibrium O tendency to stable equilibrium P+ or P- spiral line approaching P+ or P- the same as the left, but closer to rh, jumping back and forth between P+ and P-, a transient chaos, ultimately approaching P+ or P- unstable limit cycles (subcritical Hopf bifurcation) leading to chaos kinetic energy minimum upgrowth increase sustained increase Casimir function minimum gradual increases increase sustained increase sum of D1 and D2 inexistence monotone increase increase upgrowth state of the water wheel nomotion irregular rotation fig. 1(a),1(b) unstable rotation fig. 1(b),1(c) chaotic rotation fig. 1(c) -
[1] LORENZ E N. Deterministic nonperiodic[J]. Journal of the Atmospheric Sciences, 1963, 20(2): 130-141. doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [2] TEMAN R. Infinite Dimensional Dynamic System in Mechanics and Physics[M]//Applied Mathematical Sciences. New York: Springer-Verlag, 2000. [3] PCHELINTSEV A N. Numerical and physical modeling of the dynamics of the Lorenz system[J]. Numerical Analysis and Applications, 2014, 7(2): 159-167. doi: 10.1134/S1995423914020098 [4] KNOBLOCH E. Chaos in the segmented disc dynamo[J]. Physics Letters A, 1981, 82(9): 439-440. doi: 10.1016/0375-9601(81)90274-7 [5] SPARROW C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors[M]. New York: Springer-Verlag, 1982. [6] MIROSLAV K, GODFREY G. Theory for the exprimental observation of chaos in a rotating water wheel[J]. Physical Review A, 1992, 45(2): 626-637. doi: 10.1103/PhysRevA.45.626 [7] HILBORN R C. Chaos and Nonlinear Dynamics[M]. Oxford: Oxford University Press, 1994. [8] LESLIE E M. The Malkus-Lorenz water wheel revisited[J]. American Association of Physics Teachers, 75(12): 1114-1122. [9] LEONOV G A, KUZNETSOV N V, KORZHEMANOVA N A, et al. Lyapunov dimension formula for the globalattractor of the Lorenz system[J]. Communications in Nonlinear Science, 2016, 41: 84-103. doi: 10.1016/j.cnsns.2016.04.032 [10] ASHISH B, VAN G R A. Chaos in a non-autonomous nonlinear system describing asymmetricwater wheels[J]. Nonlinear Dynamics, 2018, 93: 1977-1988. doi: 10.1007/s11071-018-4301-3 [11] 王贺元. Couette-Taylor流的力学机理与能量转换[J]. 数学物理学报, 2020, 40(1): 243-256. doi: 10.3969/j.issn.1003-3998.2020.01.019WANG Heyuan, Mechanical mechanism and energy conversion of Couette-Taylor flow[J]. Acta Mathematica Scientia, 2020, 40(1): 243-256. (in Chinese) doi: 10.3969/j.issn.1003-3998.2020.01.019 [12] 王贺元, 崔进. 旋转流动的低模分析及仿真研究[J]. 应用数学和力学, 2017, 38(7): 794-806. doi: 10.21656/1000-0887.360342WANG Heyuan, CUI Jin. Low-dimensional analysis and numerical simulation of rotating flow[J]. Applied Mathematics and Mechanics, 2017, 38(7): 794-806. (in Chinese) doi: 10.21656/1000-0887.360342 [13] ARNOLD V. Kolmogorov's hydrodynamic attractors[J]. Proceedings of the Royal Society of London(Series A): Mathematical and Physical Sciences, 1991, 434(1890): 19-22. doi: 10.1098/rspa.1991.0077 [14] PASINI A, PELINO V. A unified view of Kolmogorov and Lorenz systems[J]. Physics Letters A, 2000, 275 (5/6): 435-446. http://pdfs.semanticscholar.org/ab3c/c234054df2d435696491e2c93421b872c202.pdf [15] LIANG X, QI G. Mechanical analysis and energy conversion of Chen chaotic system[J]. Brazilian Journal of Physics, 2017, 47(4): 288-294. http://www.sciencedirect.com/science/article/pii/S0960077917300723 [16] LIANG X, QI G. Mechanical analysis of Chen chaotic system[J]. Chaos, Solitons and Fractals, 2017, 98: 173-177. doi: 10.1016/j.chaos.2017.03.021 [17] QI G, LIANG X. Mechanical analysis of Qi four-wing chaotic system[J]. Nonlinear Dynamics, 2016, 86(2): 1095-1106. doi: 10.1007/s11071-016-2949-0 [18] PELINO V, MAIMONE F, PASINI A. Energy cycle for the Lorenz attractor[J]. Chaos, Solitons and Fractals, 2014, 64: 67-77. doi: 10.1016/j.chaos.2013.09.005 [19] MARSDEN J E, RATIU T S. Introduction to Mechanics and Symmetry: a Basic Exposition of Classical MechanicalSystems[M]. 2nd ed. Berlin: Springer, 2002. [20] STROGATZ S H. Nonlinear Dynamics and Chaos[M]. Reading, MA: Perseus Books, 1994. [21] DOERING C R, GIBBON J D. On the shape anddimension of the Lorenz attractor[J]. Dynamics and Stability of Systems, 1995, 10(3): 255-268. doi: 10.1080/02681119508806207 [22] MORRISON P J. Thoughts on brackets and dissipation: old and new[J]. Journal of Physics: Conference Series, 2009, 169(1): 012006. -





 下载:
下载:














 渝公网安备50010802005915号
渝公网安备50010802005915号