A Study on Interfacial Fracture Behaviors of Superconducting Thin Film/Substrate Structures on Taking the Account of Effects of Flux Flow
-
摘要:
超导薄膜是一种采用化学涂层制备而成的多层薄膜结构，作为性能优越的导电功能结构材料，其载流能力与结构完整性直接相关。在超导薄膜制备过程中，超导层与金属基底之间的界面裂纹很难避免。因此，在载流运行过程中，由于外磁场的存在，这类界面裂纹的强度问题成为关键。为此，该文针对超导薄膜结构，以磁通量子穿透薄膜理论和线弹性断裂理论为基础，建立了研究超导层与基底界面裂纹强度问题的解析模型。深入分析了外加磁场作用下界面裂纹强度问题，得到了超导磁通流动对裂纹尖端应力场和能量释放率的影响。结果表明：磁通流动速度越大，界面裂纹尖端处应力越大且能量释放率越大，这将导致界面更容易发生裂纹破坏。该文所得结果有助于分析相关的界面裂纹问题。
Abstract:The superconducting thin film is a kind of multilayer structure prepared by chemical coating. As a conductive functional structure material with excellent performance, its structural integrity is directly related to the current-carrying capacity. During the preparation of superconducting thin films, it is hard to avoid the interface cracks between the superconducting layer and the metal substrate. In this case, along with the current-carrying operation, the strength of the interface crack in an external magnetic field makes a key problem. Therefore, based on the theory of flux through the thin film and the linear elastic fracture, an analytical model was established for the strength of the interface crack between the superconducting film and the substrate. The effects of the viscous flux flow on the stress field and the energy release rate at the crack tip were obtained. The results show that, the higher the flux flow velocity is, the greater the stress and the energy release rate at the crack tip of the interface will be, which will lead to crack propagation along the interface. The work is helpful for the analysis of interface cracks mentioned above.
-
Key words:
- superconducting thin film /
- flux flow /
- interface crack /
- crack tip stress
-
图 1 计算模型示意图: (a) 超导薄膜/基底结构界面裂纹问题；(b) 电磁力分布
Figure 1. The schematic drawing for calculation: (a) interface crack between superconducting thin film and substrate; (b) electromagnetic force distribution
图 2 薄膜与基底结构界面中心处裂纹计算模型示意图
Figure 2. The calculation model of a crack at the center of the interface between the thin film and the substrate
图 3 截面A的电流密度分布 (磁场上升阶段)
Figure 3. The current density distribution in cross-section A (the increasing field)
图 4 截面A的磁通密度分布 (磁场上升阶段)
Figure 4. The flux density distribution in cross-section A (the increasing field)
图 5 Ⅰ型应力强度因子KI/K0与外加磁场的关系(磁场上升阶段)
Figure 5. The relationship between mode Ⅰ stress intensity factor KI/K0 and the magnetic field (the increasing field)
图 6 Ⅱ型应力强度因子KⅡ/K0与外加磁场的关系(磁场上升阶段)
Figure 6. The relationship between mode Ⅱ stress intensity factor KⅡ/K0 and the magnetic field (the increasing field)
图 7 截面A的电流密度分布 (磁场下降阶段)
Figure 7. The current density distribution in cross-section A (the decreasing field)
图 8 截面A的磁通密度分布 (磁场下降阶段)
Figure 8. The flux density distribution in cross-section A (the decreasing field)
图 9 Ⅰ型应力强度因子KI/K0与外加磁场的关系(磁场下降阶段)
Figure 9. The relationship between mode Ⅰ stress intensity factor KI/K0 and the magnetic field (the decreasing field)
图 10 Ⅱ型应力强度因子KⅡ/K0与外加磁场的关系(磁场下降阶段)
Figure 10. The relationship between mode Ⅱ stress intensity factor KⅡ/K0 and the magnetic field (the decreasing field)
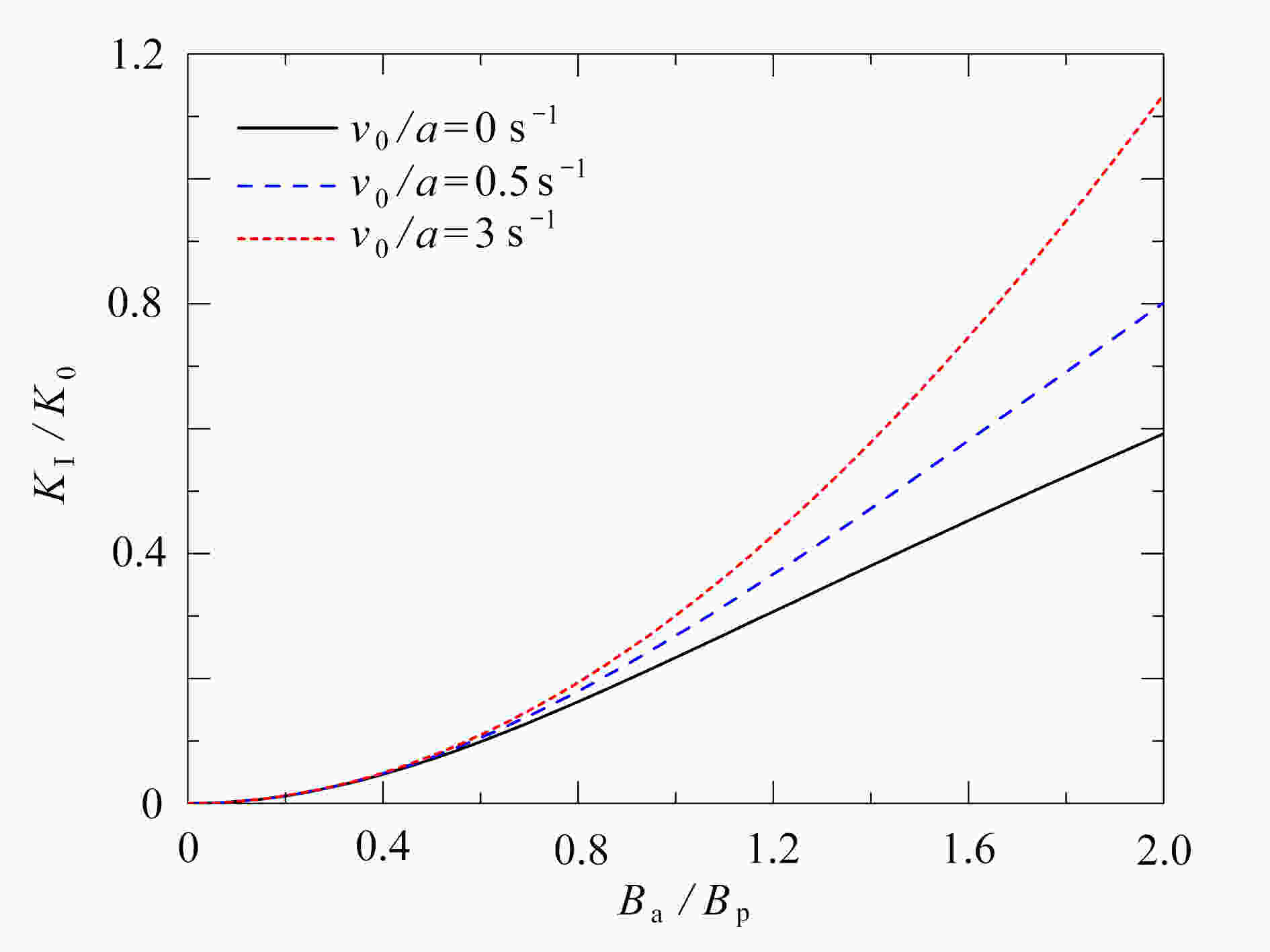
图 11 磁场上升阶段和磁场下降阶段能量释放率与外加磁场的关系：（a）
${B_{\rm{a}}} \leqslant 2.0{B_{\rm{p}}}$ ；（b）${B_{\rm{a}}} \leqslant {\text{1}}.2{B_{\rm{p}}},{\text{ }}G/{G_0} \leqslant 0.04$ Figure 11. The relationship between the energy release rate and the external magnetic field in increasing and decreasing fields:（a）
${B_{\rm{a}}} \leqslant 2.0{B_{\rm{p}}}$ ; （b）${B_{\rm{a}}} \leqslant $ $ {\text{1}}.2{B_{\rm{p}}},\;{\text{ }}G/{G_0} \leqslant 0.04$ -
[1] ZHANG Z X, XUE F, GOU X F. Interaction of two parallel cracks in REBCO bulk superconductors under applied magnetic field[J]. Chinese Physics Letters, 2016, 33(7): 077401. doi: 10.1088/0256-307X/33/7/077401 [2] 高配峰. 高温超导复合带材力学行为及变形对临界特性影响的研究[D]. 博士学位论文. 兰州: 兰州大学, 2017.GAO Peifeng. Mechanical behaviors and influence of deformation on critical properties for high temperature superconducting composite tapes[D]. PhD Thesis. Lanzhou: Lanzhou University, 2017. (in Chinese) [3] MBAM S O, GOU X F. Interface crack growth rate and fatigue life of multilayer-coated conductor tapes[J]. Engineering Fracture Mechanics, 2020, 228: 106910. doi: 10.1016/j.engfracmech.2020.106910 [4] YONG H D, ZHOU Y H. Interface crack between superconducting film and substrate[J]. Journal of Applied Physics, 2011, 110(6): 063924. doi: 10.1063/1.3634019 [5] HUTCHINSON J W, SUO Z. Mixed mode cracking in layered materials[J]. Advances in Applied Mechanics, 1991, 29: 63-191. [6] SUO Z, HUTCHINSON J W. Interface crack between two elastic layers[J]. International Journal of Fracture, 1990, 43(1): 1-18. doi: 10.1007/BF00018123 [7] 李聪, 牛忠荣, 胡宗军, 等. 求解双材料裂纹结构全域应力场的扩展边界元法[J]. 应用数学和力学, 2019, 40(8): 926-937. (LI Cong, NIU Zhongrong, HU Zongjun, et al. Computation of total stress fields for cracked bi-material structures with the extended boundary element method[J]. Applied Mathematics and Mechanics, 2019, 40(8): 926-937.(in Chinese)LI Cong, NIU Zhongrong, HU Zongjun, et al. Computation of total stress fields for cracked bi-material structures with the extended boundary element method[J]. Applied Mathematics and Mechanics, 2019, 40(8): 926-937. (in Chinese)) [8] 张厚源. 考虑层间界面失效行为的REBCO超导层合带材裂纹扩展数值研究[D]. 博士学位论文. 兰州: 兰州大学, 2020.ZHANG Houyuan. Numerical study on crack propagation of REBCO superconducting laminated tapes considering the behavior of interfacial[D]. PhD Thesis. Lanzhou: Lanzhou University, 2020. (in Chinese) [9] MA P, SU R K L, FENG W J. Crack tip enrichment functions for extended finite element analysis of two-dimensional interface cracks in anisotropic magneto-electro-elastic bimaterials[J]. Engineering Fracture Mechanics, 2016, 161: 21-39. doi: 10.1016/j.engfracmech.2016.04.038 [10] GU Y, ZHANG C Z. Novel special crack-tip elements for interface crack analysis by an efficient boundary element method[J]. Engineering Fracture Mechanics, 2020, 239: 107302. doi: 10.1016/j.engfracmech.2020.107302 [11] GRUSS S, FUCHS G, KRABBES G, et al. Superconducting bulk magnets: very high trapped fields and cracking[J]. Applied Physics Letters, 2001, 79(19): 3131-3133. doi: 10.1063/1.1413502 [12] ZELDOV E, CLEM J R, MCELFRESH M, et al. Magnetization and transport currents in thin super conducting films[J]. Physical Review B, 1994, 49(14): 9802-9822. doi: 10.1103/PhysRevB.49.9802 [13] BRANDT E H, INDENBOM M V, FORKL A. Type-Ⅱ superconducting strip in perpendicular magnetic field[J]. Europhysics Letters, 1993, 22(9): 599-610. [14] MCDONALD J, CLEM J R. Theory of flux penetration into thin films with field-dependent critical current[J]. Physical Review B, 1996, 53(13): 8643-8650. doi: 10.1103/PhysRevB.53.8643 [15] JOHANSEN T H. Flux-pinning-induced stress and strain in superconductors: long rectangular slab[J]. Physical Review B, 1999, 60(17): 11187-11190. [16] XUE F, YONG H D, ZHOU Y H. Effect of flux creep and viscous flux flow on flux-pinning-induced stress and magnetostriction in a long rectangular slab superconductor[J]. Journal of Applied Physics, 2010, 108(10): 103910. doi: 10.1063/1.3506704 [17] ZHAO Y F, XIONG K. Magnetization and stress in superconducting film under electromagnetic force with viscous flux flow[J]. Modern Physics Letters B, 2020, 34(26): 2050283. doi: 10.1142/S0217984920502838 [18] 章立源, 张金龙, 崔广霁. 超导物理学[M]. 北京: 电子工业出版社, 1995.ZHANG Liyuan, ZHANG Jinlong, CUI Guangji. Superconductivity Physics[M]. Beijing: Publishing House of Electronics Industry, 1995. (in Chinese) [19] YANG Y, XIAO L Y, LI X H. Impact of viscous flux flow on the stress in long rectangular slab superconductors[J]. Journal of Applied Physics, 2010, 107(2): 023910. doi: 10.1063/1.3284080 [20] EVANS A G, HUTCHINSON J W. The thermomechanical integrity of thin films and multilayers[J]. Acta Metallurgica et Materialia, 1995, 43(7): 2507-2530. doi: 10.1016/0956-7151(94)00444-M -
下载:
点击查看大图
计量
- 文章访问数: 415
- HTML全文浏览量: 230
- PDF下载量: 48
- 被引次数: 0
